Abstract
Haplogroup R1b-M269 comprises most Western European Y chromosomes; of its main branches, R1b-DF27 is by far the least known, and it appears to be highly prevalent only in Iberia. We have genotyped 1072 R1b-DF27 chromosomes for six additional SNPs and 17 Y-STRs in population samples from Spain, Portugal and France in order to further characterize this lineage and, in particular, to ascertain the time and place where it originated, as well as its subsequent dynamics. We found that R1b-DF27 is present in frequencies ~40% in Iberian populations and up to 70% in Basques, but it drops quickly to 6–20% in France. Overall, the age of R1b-DF27 is estimated at ~4,200 years ago, at the transition between the Neolithic and the Bronze Age, when the Y chromosome landscape of W Europe was thoroughly remodeled. In spite of its high frequency in Basques, Y-STR internal diversity of R1b-DF27 is lower there, and results in more recent age estimates; NE Iberia is the most likely place of origin of DF27. Subhaplogroup frequencies within R1b-DF27 are geographically structured, and show domains that are reminiscent of the pre-Roman Celtic/Iberian division, or of the medieval Christian kingdoms.
Similar content being viewed by others
Introduction
Although it contains ~1% of the genome length in a human male cell, the lack of recombination along most of the Y chromosome makes constructing phylogenies for genetic variation relatively easy. Coupled with a robust geographic differentiation, this trait has provided a comprehensive phylogeography of Y chromosome haplotypes (usually referred to as haplogroups), that has been thoroughly characterized. Thus, the origin, dispersal, and geographic spread of many haplogroups are known. Moreover, both the genotyping of fast-mutating short tandem repeats (STRs) in the non-recombining region of the Y chromosome (NRY), and the recent availability of ascertainment-bias-free whole sequences of the NRY have reliably added a temporal scale to the deployment of the Y-chromosome diversity. One of the most salient features of the recent evolutionary history of human Y chromosomes is that it seems to have happened in bursts, with haplogroups rising to high frequency in the wake of major lifestyle shifts and technological innovations such as the advent of the Neolithic or the recently acknowledged demographic upheaval caused by the Bronze Age in Europe1, 2.
The most frequent Y-chromosome haplogroup in W Europe is R1b-M269, with frequencies ranging from 41% (Germany) to 83% (Ireland)3. Precisely, the higher frequency of this haplogroup in W Europe rather than in E Europe or W Asia led previous authors to believe it had a post-glacial Palaeolithic origin4, 5; however, a larger STR variance in SE European and W Asian R1b-M269 chromosomes and direct TMRCA dating pointed to R1b-M269 having surfed the Neolithic wave of advance3, 6, the evidence for which other authors did not find conclusive7. Finally, direct dating from NRY sequence variation puts the origin of R1b-M269 in the Early Bronze Age, ~4500 years ago (ya)1, 8, consistent with the growing ancient DNA record, where a surge in R1b-M269 is indeed seen at that time2, 9. Note, though, that R1b-M415, a branch ancestral to R1b-M269, was found as early as 14,000 ya in Italy10 and 7,000 ya in Spain2. Moreover, lack of structure of STR variation within R1b-M26911, 12 points also to an explosive growth.
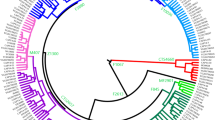
The most important branches of R1b-M269 are R1b-U106, particularly frequent in the Low Countries and NW Germany3, 13, and R1b-S116 (also known as R1b-P312), which is common throughout W Europe3. The latter trifurcates in turn into U152 (frequent in N Italy and Switzerland13), L21 (also known as M529, abundant in the British Isles7), and DF27 (Fig. 1; Supplementary Figure 1). DF27 was first discovered by citizen scientists14 and, although among the burgeoning amateur genetic genealogy it is known to be frequent in Iberian populations and their overseas offshoots, few academic publications have been devoted to it. It was found in the 1000 Genome Project populations at a frequency of 49% in Iberians, 6% in Tuscans, 7% in British, and it was absent elsewhere except for admixed populations in the Americas: Colombia (40%), Puerto Rico (36%), Mexico (10%), Perú (8%), African-Americans (4%) and Afro-Caribbeans (2%)14, 15. It was first genotyped specifically in a few Iberian populations, Brittany and Ireland as part of a study on R1b-S11616, which indeed confirmed that R1b-DF27 is present at frequencies >40% in Spain and Portugal. Subsequently, 12 SNPs within DF27 were genotyped in four N Spanish populations17, confirming its high frequency and hinting at some substructure within the Iberian Peninsula. As for its presence elsewhere, the frequency of R1b-S116 (xL21, U152) can be used as an upper bound for the frequency of R1b-DF27. R1b-S116 (x L21, U152) was found at frequencies 0–10% in Germany3, 18, 7% in the Netherlands3, 8–12% in Flanders19, 6–12% in Switzerland3, and 1–12% in Italy3, 20.
Here, by extending population sampling to cover France as well as by improving coverage in the Iberian Peninsula, we aim to i) further characterize the spatial distribution of R1b-DF27, ii) estimate its time of origin, and iii) explicitly model its expansion in relation both to its phylogenetic context, and to the demographic events that thoroughly reshaped the genetic diversity of W Europe around 4500 ya.
Results
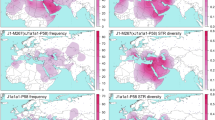
Over one thousand individuals carrying DF27 were typed for six additional SNPs (Table 1, Fig. 1) and 17 Y-STRs. DF27 itself was found at frequencies 0.3–0.5 in Iberia (with a mean of 0.42), with the notable exception of native Basques, where it reached 0.74 (for this and all subsequent frequency values, see Fig. 2 and Supplementary Table 1). In France, it dropped to a range of 0.06–0.20 and a mean of 0.11. Elsewhere, it was 0.15 in Britain (but <0.01 in Ireland) and 0.08 in Tuscany. Most (50–100%, with a proportion that dropped from East to West) DF27 Y chromosomes were also derived for Z195; thus, the highest frequencies of Z195 (0.29–0.41) were reached both in the Basque Country and in E Iberia (Catalonia, Valencia), and it becomes as rare in Portugal as it is in France. Conversely, the highest frequencies of R1b-DF27* (xZ195) are found in Native Basques and Western Iberian populations such as Asturias, Portugal and Galicia, which may harbor yet unknown branches of R1b-DF27. In turn, Z195 splits into two branches, namely L176.2 and Z220 (Fig. 1). Note that L176 is a recurrent mutation that defines two clades in the Y phylogeny: L176.1 within R1a, and L176.2 under R1b-DF27; throughout this manuscript, we will refer exclusively to the latter. L176.2 and Z220 peak, respectively, in E Iberia and the Basque Country. L176.2 is further subdivided into M167 (SRY2627, ref. 21), with the highest frequencies in Catalonia and the lands settled from Catalonia in the 13th century (Valencia, the Balearics). This marker had been typed in a number of Iberian and other European populations4, 18,19,20, 22,23,24,25, and the overall frequency pattern found (Supplementary Figure 1) confirms a distribution centred in the eastern half of Iberia, although with higher frequencies (up to 0.16) in the upper Ebro river valley and the Pyrenees. As mentioned above, Z220 is most frequent in the Basque Country (0.28), and a similar pattern is found for its successive nested clades, namely Z278 and M153. For the latter, available additional data22, 23, 25 showed it confined to the Iberian Peninsula, with frequencies 0.06–0.40 among Basque subpopulations, but rarely above 0.01 elsewhere (Supplementary Figure 1).
Contour maps of the derived allele frequencies of the SNPs analyzed in this manuscript. Population abbreviations as in Table 1. Maps were drawn with SURFER v. 12 (Golden Software, Golden CO, USA).
The subhaplogroup frequencies were summarized in a PC plot (Fig. 3). The first PC separated the Iberian populations (save for the three westernmost samples, namely Portugal, Galicia, and Asturias) from the rest, explained 68.6% of the total variation, and was positively correlated with DF27 and all of its subhaplogroups. On the contrary, PC2 (20.9%) was positively correlated with L176.2 and M167 and most negatively correlated with Z278 and M153, and separated most Eastern Iberian populations from the rest.
Principal component analysis of subhaplogroup frequencies. Population abbreviations as in Table 1. Circles: Iberian populations; squares: non-Iberian populations.
In order to quantify the structure of subhaplogroup frequencies, we performed AMOVA with several population groupings. Thus, if we compared Iberian populations vs. the rest, the proportion of the variance explained by the differences among these two groups (i.e., F CT ) was 12.40% (p < 10−4), while the proportion of the variance found within groups (i.e., F SC ) was 3.20% (p < 10−4). If the native Basques were split from the Iberians, then F CT = 13.57% (p < 10−4) and F SC = 1.37% (p < 10−4). Finally, if Eastern Iberians are also split from the rest of Iberians, then F CT = 11.68% (p < 10−4) and F SC = 0.31% (p = 0.0106). In conclusion, the differences among the groups that are apparent in the PCA plot are highly statistically significant.
Haplotypes comprising 17 Y-STRs were available for 758 individuals (Table 2). AMOVA among this set of populations gave R ST = 0.72% (p = 0.00386), while, for the same populations, subhaplogroup frequencies yielded F ST = 8.33% (p < 10−4). Thus, Y-STRs seem to capture much less phylogeographic structure than SNPs themselves, as described for R1b-M26911, 12. Still, some Y-STR structure may be present within R1b-DF2712, 17. Since a median-joining tree with 688 different haplotypes is unmanageable, we resorted to principal component analysis (PCA) among haplotypes (Fig. 4). The first PC explained 15.1% of the STR variation and correlated mostly with DYS437 (r = 0.865), DYS448 (r = 0.858), and YGATAH4 (r = 0.724), and separated haplotypes that carried the derived allele for Z220 (that is, belonging to R1b-Z220*, R1b-Z278* and R1b-M153) from the rest. PC1 coordinates were highly significantly different by subhaplogroup (p ~ 10−150, ANOVA). The median haplotype for Z220-derived chromosomes was 11-14-18 at YGATAH4-DYS437-DYS448 while it was 12-15-19 for the rest of DF27 chromosomes (other STRs showed the same median allele). PC2 explained 8.6% of the STR variation and correlated with DYS390 (r = 0.647) and DYS456 (r = −0.544), and separated R1b-Z220* from R1b-Z278* chromosomes; overall, R1b-DF27 subhaplogroups had significantly different PC2 coordinates (p = 9.12 × 10−4). The same PC results can also be analyzed by population (Fig. 4b): PC1 coordinates are statistically significantly different by population (ANOVA, p = 0.00512), with the French samples having higher, positive values in this PC, while PC2 is not significant across populations (p = 0.781). These results can be explained by the very low frequency of Z220-derived chromosomes outside of Iberia.
Internal diversity and ages of DF27 and its derived subhaplogroups
The average STR variance of DF27 and each subhaplogroup is presented in Suppl. Table 2. As expected, internal diversity was higher in the deeper, older branches of the phylogeny. If the same diversity was divided by population, the most salient finding is that native Basques (Table 2) have a lower diversity than other populations, which contrasts with the fact that DF27 is notably more frequent in Basques than elsewhere in Iberia (Suppl. Table 1). Diversity can also be measured as pairwise differences distributions (Fig. 5). The distribution of mean pairwise differences within Z195 sits practically on top of that of DF27; L176.2 and Z220 have similar distributions, as M167 and Z278 have as well; finally, M153 shows the lowest pairwise distribution values. This pattern is likely to reflect the respective ages of the haplogroups, which we have estimated by a modified, weighted version of the ρ statistic (see Methods).
We estimated an age of 4190 ± 140 ya for the whole of DF27. This figure is remarkably similar both to the estimate (4128 ± 71 ya) that can be produced from whole Y-chromosome sequence variability in the 88 DF27-derived individuals present overall in the 1000 genomes project dataset, and to the age estimated from 201 individuals in our dataset for which 21 non-duplicated Y-STRs from the Powerplex Y23 System were available26 (3880 ± 165).
Z195 seems to have appeared almost simultaneously within DF27, since its estimated age is actually older (4570 ± 140 ya). Of the two branches stemming from Z195, L176.2 seems to be slightly younger than Z220 (2960 ± 230 ya vs. 3320 ± 200 ya), although the confidence intervals slightly overlap. M167 is clearly younger, at 2600 ± 250 ya, a similar age to that of Z278 (2740 ± 270 ya). Finally, M153 is estimated to have appeared just 1930 ± 470 ya.
Haplogroup ages can also be estimated within each population, although they should be interpreted with caution (see Discussion). For the whole of DF27, (Table 3), the highest estimate was in Aragon (4530 ± 700 ya), and the lowest in France (3430 ± 520 ya); it was 3930 ± 310 ya in Basques. Z195 was apparently oldest in Catalonia (4580 ± 240 ya), and with France (3450 ± 269 ya) and the Basques (3260 ± 198 ya) having lower estimates. On the contrary, in the Z220 branch, the oldest estimates appear in North-Central Spain (3720 ± 313 ya for Z220, 3420 ± 349 ya for Z278). The Basques always produce lower estimates, even for M153, which is almost absent elsewhere.
R1b-DF27 and demography
We tested the dynamics of R1b-DF27 by means of Approximate Bayesian Computing (ABC). In particular, we compared two simple models: constant population size vs. growth since time Tstart. Both the rejection and the regression method undoubtedly favoured the growth model, with associated posterior probabilities that were never lower than 0.99. The principal component analysis (PCA) of the first 3,000 best simulations from each model (i.e. the 3,000 simulation closest to the observed dataset that are generated by each model) actually shows that the point corresponding to the observed data falls in the middle of the results obtained simulating growth, thus confirming that the growth model is also able to generate the observed variation (Suppl. Fig. 2). We then estimated the demographic parameters associated with the growth model. The median value for Tstart has been estimated at 103 generations (Table 4), with a 95% highest probability density (HPD) range of 50–287 generations; effective population size increased from 131 (95% HPD: 100–370) to 72,811 (95% HPD: 52,522–95,334). Considering patrilineal generation times of 30–35 years27, our results indicate that R1b-DF27 started its expansion ~3,000–3,500 ya, shortly after its TMRCA.
As a reference, we applied the same analysis to the whole of R1b-S116, as well as to other common haplogroups such as G2a, I2, and J2a. Interestingly, all four haplogroups showed clear evidence of an expansion (p > 0.99 in all cases), all of them starting at the same time, ~50 generations ago (Table 4), and with similar estimated initial and final populations. Thus, these four haplogroups point to a common population expansion, even though I2 (TMRCA, weighted ρ, 7,800 ya) and J2a (TMRCA, 5,500 ya) are older than R1b-DF27. It is worth noting that the expansion of these haplogroups happened after the TMRCA of R1b-DF27.
Discussion
We have characterized the geographical distribution and phylogenetic structure of haplogroup R1b-DF27 in W. Europe, particularly in Iberia, where it reaches its highest frequencies (40–70%). The age of this haplogroup appears clear: with independent samples (our samples vs. the 1000 genome project dataset) and independent methods (variation in 15 STRs vs. whole Y-chromosome sequences), the age of R1b-DF27 is firmly grounded around 4000–4500 ya, which coincides with the population upheaval in W. Europe at the transition between the Neolithic and the Bronze Age2, 9. Before this period, R1b-M269 was rare in the ancient DNA record, and during it the current frequencies were rapidly reached2, 9, 10. It is also one of the haplogroups (along with its daughter clades, R1b-U106 and R1b-S116) with a sequence structure that shows signs of a population explosion or burst1. STR diversity in our dataset is much more compatible with population growth than with stationarity, as shown by the ABC results, but, contrary to other haplogroups such as the whole of R1b-S116, G2a, I2 or J2a, the start of this growth is closer to the TMRCA of the haplogroup. Although the median time for the start of the expansion is older in R1b-DF27 than in other haplogroups, and could suggest the action of a different demographic process, all HPD intervals broadly overlap, and thus, a common demographic history may have affected the whole of the Y chromosome diversity in Iberia. The HPD intervals encompass a broad timeframe, and could reflect the post-Neolithic population expansions from the Bronze Age to the Roman Empire28.
While when R1b-DF27 appeared seems clear, where it originated may be more difficult to pinpoint. If we extrapolated directly from haplogroup frequencies, then R1b-DF27 would have originated in the Basque Country; however, for R1b-DF27 and most of its subhaplogroups, internal diversity measures and age estimates are lower in Basques than in any other population. Then, the high frequencies of R1b-DF27 among Basques could be better explained by drift rather than by a local origin (except for the case of M153; see below), which could also have decreased the internal diversity of R1b-DF27 among Basques. An origin of R1b-DF27 outside the Iberian Peninsula could also be contemplated, and could mirror the external origin of R1b-M269, even if it reaches there its highest frequencies. However, the search for an external origin would be limited to France and Great Britain; R1b-DF27 seems to be rare or absent elsewhere: Y-STR data are available only for France, and point to a lower diversity and more recent ages than in Iberia (Table 3). Unlike in Basques, drift in a traditionally closed population seems an unlikely explanation for this pattern, and therefore, it does not seem probable that R1b-DF27 originated in France. Then, a local origin in Iberia seems the most plausible hypothesis. Within Iberia, Aragon shows the highest diversity and age estimates for R1b-DF27, Z195, and the L176.2 branch, although, given the small sample size, any conclusion should be taken cautiously. On the contrary, Z220 and Z278 are estimated to be older in North Central Spain (N Castile, Cantabria and Asturias). Finally, M153 is almost restricted to the Basque Country: it is rarely present at frequencies >1% elsewhere in Spain (although see the cases of Alacant, Andalusia and Madrid, Suppl. Table 1), and it was found at higher frequencies (10–17%) in several Basque regions25; a local origin seems plausible, but, given the scarcity of M153 chromosomes outside of the Basque Country, the diversity and age values cannot be compared.
Within its range, R1b-DF27 shows same geographical differentiation: Western Iberia (particularly, Asturias and Portugal), with low frequencies of R1b-Z195 derived chromosomes and relatively high values of R1b-DF27* (xZ195); North Central Spain is characterized by relatively high frequencies of the Z220 branch compared to the L176.2 branch; the latter is more abundant in Eastern Iberia. Taken together, these observations seem to match the East-West patterning that has occurred at least twice in the history of Iberia: i) in pre-Roman times, with Celtic-speaking peoples occupying the center and west of the Iberian Peninsula, while the non-Indoeuropean eponymous Iberians settled the Mediterranean coast and hinterland; and ii) in the Middle Ages, when Christian kingdoms in the North expanded gradually southwards and occupied territories held by Muslim fiefs.
The relevance and possible applications of R1b-DF27
Although R1b-DF27 as a whole has remained relatively obscure in the academic literature, two of the SNPs it contains, namely M167 (SRY2627) and M153 have accrued quite a number of studies. Thus, excluding this paper, M153 has been typed in 42 populations, for a total of 3,117 samples22, 23, 25, 29, 30; M167 has been typed in at least 113 populations and 10,379 individuals4, 18,19,20, 22,23,24,25, 29,30,31. It is not obvious then why both markers are absent from Y-phylotree (http://www.phylotree.org/Y/tree/index.htm, ref. 32), which is the current academic Y-chromosome haplogroup reference tree and which contains within DF27 a number of much more obscure SNPs.
Potentially, a SNP with relatively high frequencies in Iberian and Iberian-derived populations and rarer elsewhere could be applied in a forensic genetics setting to infer the biogeographic origin of an unknown contributor to a crime scene33. However, neither the specificity nor the sensitivity of such an application would guarantee significant investigative leads in most cases. When compared to the 1000 genomes CEU sample of European-Americans15, R1b-DF27 is just 4.19 times more frequent in Iberians than in CEU, a ratio that raises to 6.82 for R1b-Z220 (which, though, has a frequency of only 13.9% in Iberians). Probably, other types of evidence of the involvement of a person of interest of Iberian descent would be needed to justify tying R1b-DF27.
R1b-DF27 may also be used to trace migratory events involving Spanish or Portuguese men, particularly outside of Western Europe; a clear example can be seen the Latin American populations (see the Introduction section), where R1b-DF27 seems to correlate with the amount of male-mediated Spanish admixture: it is clearly less frequent in the populations with a stronger Native American component, such as Mexico and Peru. Even within Europe, Y haplogroup frequencies have been used to detect short-range migration events, such as that from Northern France to Flanders34. Thus, the traces of the medieval expansion of the Aragon kingdom towards the Mediterranean in the 14th–15th centuries, or the Castilian occupation of Flanders in the 17th century may be traced through the male lineages, R1b-DF27 in particular.
Finally, the Y chromosome in often studied in connection with surnames, since the latter are also often transmitted through the male line35. For that, Y-STR haplotypes are analyzed, and, given the Y-STR mutation rates, similarity in Y-STR haplotypes between men sharing the same surname is taken as indicative of a shared genealogical origin36, 37. However, diversity in Y-STR haplotypes within the R1b-M269 branch is rather small11, 12, and the sole use of Y-STRs may result in homoplasy, rather than shred origin, causing Y-STR haplotype convergence. Thus, particularly within Iberia, R1b-DF27 should be used when trying to ascertain the founding events of surnames. No SNP deeper than R1b-M269 was typed in a survey of Spanish surnames38, while some SNPs in the R1b-DF27 branch (Z195, Z220, Z278, M153 and M167) were used in a similar study27.
Although we have contributed to the understanding of the phylogeography of R1b-DF27, which makes up a dominant fraction of Iberian (and Latin American) Y chromosomes, better tools and designs would be needed to solve some of the issues we discussed above. In particular, we genotyped pre-ascertained SNPs, and a global characterization of the whole sequence diversity of this haplogroup would allow more precise statistical analyses to be run. Also, a more comprehensive sampling scheme, including more information from Atlantic Iberia, would be desirable to obtain a more accurate picture of this haplogroup.
Methods
Samples/ethics
The population samples we analyzed comprised a total of 2990 individuals, of which 1072 carried the derived allele at the DF27 SNP. Additionally, 55 individuals with partial information were used to estimate subhaplogroup frequencies (see below). These samples cover the Iberian Peninsula and France, and were originally described in16, 27, 39 (Table 1, Fig. 2). Also, subhaplogroup frequencies were estimated for the British (GBR) and Tuscan (TSI) samples of the 1000 genomes project15. Informed consent for study participation was obtained from all the subjects; Internal Review Board approval for this work was granted by Faculty of Pharmacy UPV/EHU, September 26th 2008; CEISH/119/2012, BNADN Ref. 12/0031; and CEIC-PSMAR ref. 2016/6723/I. This research was conducted under the principles of the Helsinki declaration.
SNP genotyping
All samples were typed for SNPs/indels M269, S116 (P312), DF27, Z195, L176, M167 (SRY2627), Z220 (S356), Z278, and M153 (Fig. 1). DF27, Z195, L176, M167, Z220, Z278, and M153 were typed in samples from Portugal, Andalusia, Galicia, Madrid, and part of the Alacant and Barcelona samples as described in ref. 17. The original genotyping of the French samples (except Brittany)39 was supplemented with the SNPs in the Open Array panel described in ref. 27. Subsequently, the French samples plus others from Eastern Iberia (see Table 1) were genotyped for DF27 and L176 by Sanger sequencing, since these polymorphisms were not part of the original Open Array panel. Both were amplified using 2.5 μl buffer, 2 μl dNTPs, 1.25 μl each of forward/reverse primers, 1.5 μl MgCl2, 0.2 μl Taq polymerase, 1.5 μl DNA, and 14.8 μl H2O. DF27 was first amplified with a nested PCR to reduce non-specific amplifications. The nested PCR involves two sets of primers used in two successive PCR amplifications, namely outer DF27 forward: GGGAATTTGATCCTGTCGTTG, outer DF27 reverse: GAACAAAGCCTCCAAGAAATATGAGG, M13F-tagged nested DF27 forward: TGTAAAACGACGGCCAGTTATTTTATTTCTCCTTCACTTATA, nested DF27 Reverse: ATCCAGGAGAACTTCCCCAATC. In the first PCR, 30 cycles were performed at 95 °C (30 sec), 60.5 °C (30 sec), and 72 °C (40 sec); in the second PCR, the annealing temperature was lowered to 59.2 °C. For L176, primers were L176 Forward: CAACAGGCCAGAAGGAACAG and L176 reverse: TTACAGGTGGAATGGGGTGT; the annealing temperature was 58.3 °C, and times and number of cycles were the same as in DF27.
Genotypes for 17 short tandem repeats (STRs) contained in the AmpFlSTR®YFiler® PCR Amplification kit (Applied Biosystems) were available for most populations (see Table 1)16, 26, 27, 39,40,41. The dataset generated during the current study is available from the corresponding author on reasonable request.
Statistics
For most populations, the frequencies of DF27 and its subhaplogroups were estimated by direct counting. However, in some populations, individuals with partial information were present: in some cases, no SNP information was available, but they could be inferred to carry R1b from their STR haplotypes42, 43; further subhaplogroup inference is precluded by the high homogeneity of STR haplotypes within R1b-M26911, 12. In other cases, individuals were known to be S116 (xZ195, L21, U152) or Z195 (xM167, Z220), but further genotyping for DF27 or L176 failed. The relative proportions of cases with full genotypes over R1b, S116 or Z195 were used to estimate the probabilities of each individual with missing genotypes to belong to each possible subhaplogroup. Using these probabilities as frequencies, the frequency of each subhaplogroup was estimated. Detailed formulas for each subhaplogroup are given in Supplementary note 1. Individuals with missing information were used only to refine the estimation of subhaplogroup frequencies.
Haplogroup frequency maps were drawn with SURFER v. 12 (Golden Software, Golden CO, USA) by krigging. Principal component analysis was performed with IBM SPSS Statistics v. 19. Basic descriptive statistics, as well as AMOVA, were computed with Arlequin 3.544. Haplogroups were dated from STR variation with ρw, a weighted version of ρ45 that leverages on the relatively precise knowledge of the mutation rate of each Y-STR. Thus, it takes into account that mutations at slow STRs take longer to accumulate than mutations at faster STRs. It is defined as
where N is the number of chromosomes, k is the number of different haplotypes, n i is the absolute frequency of the ith haplotype, S is the number of different STRs, X ji is the allelic state of the ith haplotype at the jth STR, X jm is the median allele at the jth STR, \(\bar{\mu }\) is the average mutation rate and μ j is the mutation rate of the jth STR. The standard deviation of ρ W is given by
And age, as in ref. 45, is estimated as
where \(\bar{\mu }\) is now expressed in years per mutation. ρ W was computed with an ad hoc R script, which is available in github (http://github.com/fcalafell/weighted_rho). Mutation rates were retrieved from the Y-Chromosome STR Haplotype Database (YHRD, www.yhrd.org) on Feb. 1, 2017. DYS385 was omitted from the calculations, and DYS389I was subtracted from DYS389II. Additionally, outlier individuals were detected and removed from the estimate as suggested in ref. 20.
Unweighted ρ was used to estimate the age of DF27 by using the whole Y chromosome sequences of the 88 unrelated individuals derived for this SNP and present in the 1000 genomes project dataset. The mutation rate considered was 0.888 × 10−9 per year1, 46, which, taking into account the ~10.36 Mb of the Y chromosome amenable to short-read sequencing and SNP detection1, translates to a rate of 108.7 years/mutation.
Approximate Bayesian Computing (ABC) was used to test alternative demographic models and to estimate their parameters. One million simulations were run with fastsimcoal2 47, 48, either with a constant population size (drawn from a lognormal distribution between 100 and 100,000), or with an exponential growth that started Tstart generation ago. In the growth model, the effective population sizes before (Na) and at the end (Nc) of the growth were drawn in the same fashion of the constant model, and conditioned to Na < Nc. Na refers to a time Tstart drawn from a uniform distribution between 50 and 350 generations. STR mutation rates were taken as fixed given the high precision with which they are known, but the value of the geometric parameter for the Generalized Stepwise Mutation model was sampled from a uniform distribution with limits (0; 0.8). To summarize the data, we calculated the mean and the standard deviation over loci of four statistics: the number of different haplotypes (K), the haplotype diversity (H), the allelic range and the Garza- Williamson’s index. We calculated posterior probabilities of the models by means of the simple rejection algorithm49 as well as of the weighted multinomial logistic regression50, evaluating different thresholds for both methods to check the stability of the results as in ref. 51. For parameter estimation, we calculated the Euclidian distance between the simulated and observed summary statistics and retained the 5% of the total simulations corresponding to the shortest distances. Posterior probability for each parameter was estimated using a weighted local regression52, after a logtan transformation53.
References
Poznik, G. D. et al. Punctuated bursts in human male demography inferred from 1,244 worldwide Y-chromosome sequences. Nat. Genet. 48, 593–599 (2016).
Haak, W. et al. Massive migration from the steppe was a source for Indo-European languages in Europe. Nature 522, 207–211 (2015).
Myres, N. M. et al. A major Y-chromosome haplogroup R1b Holocene era founder effect in Central and Western Europe. Eur. J. Hum. Genet. 19, 95–101 (2011).
Rosser, Z. H. et al. Y-chromosomal diversity in Europe is clinal and influenced primarily by geography, rather than by language. Am. J. Hum. Genet. 67, 1526–1543 (2000).
Semino, O. et al. The genetic legacy of Paleolithic Homo sapiens sapiens in extant Europeans: a Y chromosome perpective. 290, 1155–1159 (2000).
Balaresque, P. et al. A predominantly neolithic origin for European paternal lineages. PLoS Biol 8, e1000285 (2010).
Busby, G. B. J. et al. The peopling of Europe and the cautionary tale of Y chromosome lineage R-M269. Proc. R. Soc. B Biol. Sci. 279, 884–892 (2012).
Batini, C. et al. Large-scale recent expansion of European patrilineages shown by population resequencing. Nat. Commun. 6, 7152 (2015).
Allentoft, M. E. et al. Population genomics of Bronze Age Eurasia. Nature 522, 167–172 (2015).
Fu, Q. et al. The genetic history of Ice Age Europe. Nature 534, 200–5 (2016).
Larmuseau, M. H. D. et al. Recent Radiation within Y-chromosomal Haplogroup R-M269 Resulted in High Y-STR Haplotype Resemblance. Ann. Hum. Genet. 78, 92–103 (2014).
Solé-Morata, N., Bertranpetit, J., Comas, D. & Calafell, F. Recent radiation of R-M269 and high Y-STR haplotype resemblance confirmed. Ann. Hum. Genet. 78 (2014).
Cruciani, F. et al. Strong intra- and inter-continental differentiation revealed by Y chromosome SNPs M269, U106 and U152. Forensic Sci. Int. Genet. 5, e49–52 (2011).
Rocca, R. A. et al. Discovery of Western European R1b1a2 Y chromosome variants in 1000 genomes project data: an online community approach. PLoS One 7, e41634 (2012).
Auton, A. et al. A global reference for human genetic variation. Nature 526, 68–74 (2015).
Valverde, L. et al. New clues to the evolutionary history of the main European paternal lineage M269: dissection of the Y-SNP S116 in Atlantic Europe and Iberia. Eur. J. Hum. Genet. 24, 437–41 (2016).
Villaescusa, P. et al. Characterization of the Iberian Y chromosome haplogroup R-DF27 in Northern Spain. Forensic Sci. Int. Genet. 27, 142–148 (2017).
Rębała, K. et al. Contemporary paternal genetic landscape of Polish and German populations: from early medieval Slavic expansion to post-World War II resettlements. Eur. J. Hum. Genet. 21, 415–22 (2013).
Larmuseau, M. H. D. et al. Increasing phylogenetic resolution still informative for Y chromosomal studies on West-European populations. Forensic Sci. Int. Genet. 9, 179–185 (2014).
Boattini, A. et al. Uniparental markers in Italy reveal a sex-biased genetic structure and different historical strata. PLoS One 8, e65441 (2013).
Hurles, M. E. et al. Substantial recent male-mediated gene flow between Basque and Catalan populations suggestes by analysis of a Y-chromosomal polymorphism. 65, 1437–1448 (1999).
Flores, C. et al. Reduced genetic structure of the Iberian peninsula revealed by Y-chromosome analysis: implications for population demography. Eur. J. Hum. Genet. 12, 855–63 (2004).
Alonso, S. et al. The place of the Basques in the European Y-chromosome diversity landscape. Eur. J. Hum. Genet. 13, 1293–1302 (2005).
Beleza, S. et al. Micro-phylogeographic and demographic history of Portuguese male lineages. Ann. Hum. Genet. 70, 181–94 (2006).
Martínez-Cruz, B. et al. Evidence of pre-Roman tribal genetic structure in Basques from uniparentally inherited markers. Mol. Biol. Evol. 29, 2211–22 (2012).
Purps, J. et al. A global analysis of Y-chromosomal haplotype diversity for 23 STR loci. Forensic Sci. Int. Genet. 12, 12–23 (2014).
Solé-Morata, N., Bertranpetit, J., Comas, D. & Calafell, F. Y-chromosome diversity in Catalan surname samples: insights into surname origin and frequency. Eur. J. Hum. Genet. 23, 1549–57 (2015).
McEvedy, C. & Jones, R. Atlas of world population history. (Penguin, 1978).
Adams, S. M. et al. The genetic legacy of religious diversity and intolerance: paternal lineages of Christians, Jews, and Muslims in the Iberian Peninsula. Am. J. Hum. Genet. 83, 725–736 (2008).
Bekada, A. et al. Introducing the Algerian mitochondrial DNA and Y-chromosome profiles into the North African landscape. PLoS One 8, e56775 (2013).
Varzari, A. et al. Paleo-Balkan and Slavic contributions to the genetic pool of Moldavians: insights from the Y chromosome. PLoS One 8, e53731 (2013).
van Oven, M., Van Geystelen, A., Kayser, M., Decorte, R. & Larmuseau, M. H. D. Seeing the wood for the trees: a minimal reference phylogeny for the human Y chromosome. Hum. Mutat. 35, 187–91 (2014).
Kayser, M. Forensic use of Y-chromosome DNA: a general overview. Hum. Genet. 136, 621–635 (2017).
Larmuseau, M. H. D. et al. In the name of the migrant father—Analysis of surname origins identifies genetic admixture events undetectable from genealogical records. Heredity (Edinb). 109, 90–95 (2012).
Calafell, F. & Larmuseau, M. H. D. The Y chromosome as the most popular marker in genetic genealogy benefits interdisciplinary research. Hum. Genet. 136, 559–573 (2017).
King, T. E. & Jobling, M. A. Founders, drift, and infidelity: the relationship between Y chromosome diversity and patrilineal surnames. Mol. Biol. Evol. 26, 1093–1102 (2009).
McEvoy, B. & Bradley, D. G. Y-chromosomes and the extent of patrilineal ancestry in Irish surnames. Hum. Genet. 119, 212–219 (2006).
Martinez-Cadenas, C. et al. The relationship between surname frequency and Y chromosome variation in Spain. Eur. J. Hum. Genet. 24, 120–128 (2016).
Ramos-Luis, E. et al. Y-chromosomal DNA analysis in French male lineages. Forensic Sci. Int. Genet. 9, 162–168 (2014).
Núñez, C. et al. Reconstructing the population history of Nicaragua by means of mtDNA, Y-chromosome STRs, and autosomal STR markers. Am. J. Phys. Anthropol. 143, 591–600 (2010).
Nuñez, C. et al. Highly discriminatory capacity of the PowerPlex® Y23 System for the study of isolated populations. Forensic Sci. Int. Genet. 17, 104–107 (2015).
Athey, T. W. Haplogroup prediction from Y-STR values using an allele-frequency approach. J. Genet. Geneal. 1, 1–7 (2005).
Athey, T. W. Haplogroup prediction from Y-STR values using a Bayesian allele frequency approach. J. Genet. Geneal. 2, 34–39 (2006).
Excoffier, L. & Lischer, H. E. L. Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol. Ecol. Resour. 10, 564–567 (2010).
Saillard, J., Forster, P., Lynnerup, N., Bandelt, H. J. & Nørby, S. mtDNA variation among Greenland Eskimos: the edge of the Beringian expansion. Am. J. Hum. Genet. 67, 718–726 (2000).
Helgason, A. et al. The Y-chromosome point mutation rate in humans. Nat. Genet. 47, 453–7 (2015).
Excoffier, L. & Foll, M. fastsimcoal: a continuous-time coalescent simulator of genomic diversity under arbitrarily complex evolutionary scenarios. Bioinformatics 27, 1332–1334 (2011).
Excoffier, L., Dupanloup, I., Huerta-Sánchez, E., Sousa, V. C. & Foll, M. Robust demographic inference from genomic and SNP data. PLoS Genet. 9, e1003905 (2013).
Pritchard, J. K., Seielstad, M. T., Perez-Lezaun, A. & Feldman, M. W. Population growth of human Y chromosomes: a study of Y chromosome microsatellites. Mol. Biol. Evol. 16, 1791–8 (1999).
Beaumont, M. A. In Simulation, Genetics and Human Prehistory (eds Matsamura, S., Forster, P. & Renfrew, C.) 135–154 (McDonald Institute for Archaeological Research, 2008).
Vai, S. et al. Genealogical Relationships between Early Medieval and Modern Inhabitants of Piedmont. PLoS One 10, e0116801 (2015).
Beaumont, M. A., Zhang, W. & Balding, D. J. Approximate Bayesian computation in population genetics. Genetics 162, 2025–35 (2002).
Hamilton, G. et al. Bayesian estimation of recent migration rates after a spatial expansion. Genetics 170, 409–17 (2005).
Jiménez, S., Bañón, E. & Huertas, L. Analysis of 8 Y-chromosome str loci in population from alicante (Spain). Forensic Sci. Int. Genet. Suppl. Ser. 1, 217–218 (2008).
Acknowledgements
We want to thank the thousands of volunteers who made this work possible. Cristina de Vasconcelos superbly organized the logistics of collecting part of the samples used in this paper. Funding was provided by the Agencia Estatal de Investigación and Fondo Europeo de Desarollo Regional (FEDER) (grants CGL2013-44351-P, CGL2016-75389-P), by Agència de Gestió d’Ajuts Universitaris i de la Recerca (Generalitat de Catalunya) grant 2014 SGR 866, and by the Basque Government (IT-424-07). FT was supported by the ERC Advanced Grant Agreement No 295733, ‘LanGeLin’ project.
Author information
Authors and Affiliations
Contributions
N.S.M., C.F., K.R., S.J.M., B.M.J., M.F.P., M.T.Z., A.C., M.M.P., and F.C. contributed samples. L.V., M.J.I., F.T., and S.G. participated in the design of the study and performed some of the analyses. N.S.M., P.V., C.G.F., N.F.P., and F.C. generated the dataset, performed most of the analyses, and contributed to the interpretation of the result. N.S.M., P.V., M.M.P., and F.C. designed the study and wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Solé-Morata, N., Villaescusa, P., García-Fernández, C. et al. Analysis of the R1b-DF27 haplogroup shows that a large fraction of Iberian Y-chromosome lineages originated recently in situ. Sci Rep 7, 7341 (2017). https://doi.org/10.1038/s41598-017-07710-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-07710-x
This article is cited by
-
Delineating the dispersal of Y-chromosome sub-haplogroup O2a2b-P164 among Austronesian-speaking populations
Scientific Reports (2024)
-
Chromosome-Y haplogroups in Asturias (Northern Spain) and their association with severe COVID-19
Molecular Genetics and Genomics (2024)
-
Bidirectional dispersals during the peopling of the North American Arctic
Scientific Reports (2023)
-
Contrasting maternal and paternal genetic histories among five ethnic groups from Khyber Pakhtunkhwa, Pakistan
Scientific Reports (2022)
-
Y-chromosome target enrichment reveals rapid expansion of haplogroup R1b-DF27 in Iberia during the Bronze Age transition
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.