Abstract
We propose a theoretical concept of a far-field radiative thermal rectification device that uses a phase change material to achieve a high degree of asymmetry in radiative heat transfer. The proposed device has a multilayer structure on one side and a blackbody on other side. The multilayer structure consists of transparent thin film of KBr sandwiched between a thin film of VO2 and a reflecting layer of gold. When VO2 is in its insulating phase, the structure is highly reflective due to the two transparent layers on highly reflective gold. When VO2 is in the metallic phase, Fabry-Perot type of resonance occurs and the tri-layer structure acts like a wide-angle antireflection coating achieved by destructive interference of partially reflected waves making it highly absorptive for majority of spectral range of thermal radiation. The proposed structure forms the active part of configuration that acts like a far-field radiative thermal diode. Thermal rectification greater than 11 is obtained for a temperature bias of 20 K, which is the highest rectification ever predicted for far-field radiative diode configurations.
Similar content being viewed by others
Introduction
Thermal diode1, thermal transistors2, thermal memory element3 and similar thermal analogues of electronic devices have been topic of theoretical as well as experimental works. While earlier research has been on conduction (phonon) based devices4,5,6,7,8, more recent studies have been focusing on radiation (photon) based thermal rectifiers9,10,11,12. Thermal rectification has numerous applications in thermal management, thermal logic gates13,14,15 and information processing16.
Analogous to electrical diode, thermal diode is a rectification device wherein magnitude of heat flux strongly depends on the sign of applied temperature bias. To quantify rectification, we employ the widely used definition of rectification ratio, i.e., R = (Q f − Q r )/Q r where Q f and Q r refer to forward and reverse heat flux, respectively17. Alternatively, rectification coefficient can be defined as η = (Q f − Q r )/max(Q r , Q f ). There are numerous studies pertaining to near-field and far-field thermal radiation based rectification devices that exploit temperature dependent properties of a phase change materials such as vanadium dioxide (VO2) and La0.7Ca0.15Sr0.15MnO3 (LCSMO)11, 18, 19. A number of studies deal with far-field thermal radiation20, 21 while several others focus on modulation of radiative heat transfer in the near-field regime18, 19, 22,23,24,25,26. Ben-Abdallah and Biehs introduced a VO2 based simple far-field radiative thermal diode, while Prod’homme et al.27, proposed a far-field thermal transistor that uses a VO2 base between a blackbody collector and a blackbody emitter. Zhu et al.28, showed that temperature dependent optical properties of SiC can be used to attain negative differential conductance. Van Zwol et al.22, proposed that one can take advantage of the phase transition from crystalline to amorphous state in AIST (an alloy of Ag, In, Sb, and Te) driven by a current pulse to obtain a large contrast in heat flux. In far-field limit, rectification is due to the change in emissive properties of a phase change material. In near-field limit, the difference in the coupling strength of polaritons or tunneling of surface waves between structures leads to thermal rectification. In general, it is observed that a higher rectification can be achieved in the near-field regime than in the far-field. However, it is challenging to develop such devices operating on the principle of near-field radiative transfer.
Spectral control has been studied to affect radiative heat transfer in both the far-field as well as near-field. Customization of absorption/emission spectra is often achieved by the use of multilayer thin film structures29, nanoparticles30, 31, dielectric mixtures32, 33, photonic crystals34, 35, 1-D/2-D gratings36 and metamaterials37, 38. Absorbers that utilize Fabry-Perot cavities39, 40, Salibury screens41 and Jaumann absorbers42 and ultra-thin lossy thin films bounded by transparent substrate and superstate43,44,45 have been investigated for decades. Quite notably, Nefzaoui et al.46, proposed using multilayer structures consisting of thin films (e.g., Si, HDSi and gold) to obtain thermal rectification. Kats et al.47, have theoretically and experimentally demonstrated that a thin-film of VO2 on sapphire shows strong modulation of absorbance upon phase transition, particularly, at wavelength of 11.6 μm. Taylor et al.48, recently proposed an emitter consisting a dielectric spacer between VO2 film and a reflecting substrate to achieve dynamic radiative cooling upon phase transition of VO2. Fabry-Perot resonance was achieved at 10 μm wavelength. As discussed later, we show that, by tuning the resonance at right wavelength, maximum rectification can be achieved in the proposed design.
VO2 has often been used in thermal rectification devices, because its phase-change from an insulator to a metal can be switched reversibly within a short time (~100 fs)49. The common devices use either a bulk VO2 solid or its thin-film form. In this work, we present a VO2 based far-field thermal rectification device with a simple multilayer structure. We predict a record rectification factor of greater than 11 (η > 0.91).
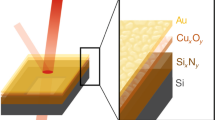
A typical far-field thermal diode has two planar components separated by a distance much larger than thermal wavelength. The active component is made of a phase-change solid, whereas the passive component stays inert. Figure 1 illustrates the vertical structure of our proposed thermal diode. The active component contains a tri-layer structure consisting of VO2, potassium bromide (KBr) and gold thin films on a substrate. Thicknesses of VO2 and KBr layers can be tuned to maximize rectification. The thickness of gold layer is fixed at 1 μm to block radiation from the substrate. For a given temperature bias, maximum (far-field) radiative heat transfer would be possible when both sides are blackbodies, while minimum heat transfer would take place when at least one side is a highly reflective mirror. Ideally, the active component should exhibit a transition from blackbody to reflective surface upon the reversal of a temperature bias which induces the phase change. This is exactly our design attempts to achieve. Therefore, the passive component is chosen to be a blackbody. Any material other than a blackbody would not yield the maximum rectification. Structure 1 and 2 are at temperature T 1 = T C + ΔT and T 2 = T C − ΔT, respectively. The mean temperature is chosen to be the phase transition temperature of VO2 (T C = 341 K). When T 1 > T 2 (referred to as forward bias), VO2 layer is in its metallic phase; and when T 1 < T 2 (reverse bias), VO2 layer becomes insulating with its optical axis aligned along the vertical direction, i.e., z-axis.
Schematic of a far-field thermal diode with a high rectification ratio. The active component has a tri-layer structure consisting of VO2, KBr and gold thin films on a substrate with thicknesses L 1, L 2 and 1 μm, respectively. The passive component is a blackbody. T c = 341 K is the phase transition temperature of VO2.
Phase transition of VO2 is not abrupt49, 50 and a complete insulator-metal transition does not occur until 350 K26. Rectification ratio depends on temperature bias as the temperature dependence of radiative heat transfer is essentially nonlinear. We calculate rectification values at a minimal temperature bias of 20 K i.e., ΔT = ±10 K. Although transition of VO2 exhibits a thermal hysteresis of about 8 K as presented in refs 49, 51, the phase transition is reversible. As we are concerned with heat flux values at 10 K above and below the critical temperature of VO2, hysteresis behavior is beyond the scope of this study.
Results and Discussion
A multilayer structure can be designed to attain high absorbance or reflectance based on its dimensions and material properties. Multilayers with constituent thicknesses much smaller than the incident wavelength of light have been studied before52. We show that in a VO2 based multilayer structure, the dramatic change in the optical property of VO2 upon phase-change facilitates an extensive variation in the surface reflectivity.
Concept shown in Fig. 1 has variable dimensions of VO2 (L 1) and KBr (L 2) layer. These dimensions were optimized by running Genetic Algorithm to maximize rectification ratio. Matlab’s optimization toolbox was used to run Genetic Algorithm to perform optimization. Default values of population size (50), fitness scaling (rank), crossover fraction (0.8), stopping criteria (100 generations) were selected in the optimization toolbox. No tuning of optimization parameters was required as number of variables was only two. Lower and upper bounds on both L 1 and L 2 were kept at 25 nm and 2 μm, respectively. Optimal dimensions were found to be L 1 = 25 nm and L 2 = 880 nm, both are practical values. Further discussion will be focused on the design with these dimensions.
Figure 2 shows spectral heat flux (dq/dλ) of the proposed thermal diode in forward and reverse direction with temperature bias 20 K (ΔT = 10 K). Forward heat flux is significantly higher than reverse flux as is clear from Fig. 2. A comparison is shown for heat flux across blackbodies at temperatures 331 K and 351 K, respectively. Inset in Fig. 2 displays angle-averaged emissivity of the active component in both scenarios. When VO2 is metallic, the structure on the active component has high emissivity near the thermal wavelength (λ th = 1.27ħc/k B T = 8.5 μm for 341 K). As a significant portion of blackbody radiation falls within this range, this gives rise to a high heat flux in forward bias. However, when VO2 is insulating, the structure has very low emissivity in the broad spectrum. The tri-layer structure behaves like a highly reflecting mirror resulting in very low heat flux. Consequently, high contrast in heat flow is achieved leading to a high rectification ratio of 11.3 (η = 0.918). In order to highlight the diode-like characteristics, heat flux across the device has been plotted against themeprature difference in Fig. 3. For comparison, simple case of bulk VO2 is also shown, it has a rectification coeffcient of η = 0.49. Note that, effect of thermal hystersis is not considered here for simplicity. Angle dependent spectral reflectivity of the active component of the thermal diode is plotted in Fig. 4 for the forward and reverse bias cases. When VO2 is metallic, the tri-layer structure acts like a wide-angle antireflection coating for wavelengths between 4 μm to 10 μm. The dark spot in Fig. 4 corresponds to Fabry-Perot type of resonance that occurs around λ = 4n KBr (λ)L 2 = 5.3 μm47. High absorption/emission in this wavelength region favors radiative heat transfer as thermal wavelength falls within this range. In reverse bias, the structure is highly reflective in a broad range of wavelengths giving rise to a very low absorption. Note that for thermal wavelength of 8.5 μm, Fabry-Perot resonance occurs (for metallic VO2) when thickness of KBr layer is L 2 = λ th /4n KBr (λ th ) = 1.4 μm. This configuration however, would not necessarily achieve maximum rectification as the structure may not be purely reflecting when VO2 is its insulating phase.
Contrasting reflective properties of the structure are due to constructive and destructive interferences of electromagnetic waves generated by partial reflections at interfaces. As an electromagnetic wave travels through the media, it is partially reflected at each interface leading to multiple reflections from each layer. This causes interference of electromagnetic waves due to each partial reflection. Effective reflection coefficient of the structure is the phasor sum of these reflection coefficients due to (an infinite number of) individual reflections. When VO2 is metallic, phasor sum of partial reflections results in destructive interference in the wavelength range of 4 μm to 10 μm. As a result, the structure is highly absorptive in the range. When VO2 is insulating, individual reflections add up to a large value making the structure highly reflective for a broad range of the spectrum.
Figure 5 shows phasor diagram of partial reflections at air-VO2 interface and VO2-KBr interface for TE polarized incident ray of wavelength λ th = 8.5 μm and angle of incidence 10°. \({\tilde{R}}_{\mathrm{1,2}}\) is the effective reflection coefficient at air-VO2 interface and \({\tilde{R}}_{\mathrm{2,3}}\) is the effective reflection coefficient at VO2-KBr interface due to multiple reflections within KBr layer. They can be expressed as geometric series whose terms are relative amplitudes of partial waves due to first, second and third reflection and so on. For both metallic as well as insulating VO2, the magnitude of \({\tilde{R}}_{\mathrm{2,3}}\), \(|{\tilde{R}}_{\mathrm{2,3}}|\), is large. However, when VO2 is in metallic phase, each partial reflection results in a phase-shift such that partial waves add up destructively leading to a small value of \(|{\tilde{R}}_{\mathrm{1,2}}|\) and low reflectivity, especially in the wavelength range centered around thermal wavelength. On the other hand, in reverse bias (insulating VO2) phasors add constructively, giving rise to highly reflective surface properties for a broad range of wavelengths. A similar phenomenon can be observed for TM polarization as well. As KBr is transparent and has a negligible extinction coefficient for most of infrared region, much of the absorption takes place within the VO2 layer. Transparent layer of KBr mainly influences the reflective properties by altering the phase of the light propagating through the media. Potentially, any other material transparent to infrared light such as magnesium fluoride or intrinsic silicon can be used in this concept. However, optimal dimensions of such a device might be different.
In summary, we present a VO2 based far-field radiative thermal diode structure with a high rectification ratio of 11.3. The active component of the proposed device has a tri-layer structure consisting thin films of VO2, KBr and gold. As VO2 undergoes phase change around 341 K, reflecting properties of the surface are dramatically changed in the spectral region that contributes to significant amount of thermal radiation. Facilitated by Fabry-Perot type of resonance around 5.3 μm, metallic VO2 makes the structure behave like a wide-angle antireflection coating while insulating VO2 makes it highly reflecting. As a result, high degree of asymmetry in radiative heat transfer is predicted across the tri-layer structure and a blackbody. Contrasting reflecting properties of the structure can be explained using constructive and destructive interference of partial reflections across the interfaces. We optimized layer thicknesses to maximize rectification. Thermal rectification greater than 11 is predicted for temperature difference of 20 K and it is highest among far-field radiative diodes that have been studied. Possibility of attaining higher rectification could be investigated in future by using alternate transparent materials, thinner films of VO2 and/or using more number of alternating VO2/dielectric layers. Such devices can find numerous applications such as thermal logic devices and thermal management systems.
Methods
To calculate heat flux in forward and reverse bias across our far-field thermal diode, we use the well known expression of radiative transfer obtained through dyadic Green’s function formalism53. Radiative transfer between two planar objects is given by
where Θ(ω, T) = (ħω/2)coth(ħω/2k B T) is the energy of a harmonic oscillator at frequency ω and temperature T, ħ is the reduced Planck constant, and k B is the Boltzmann constant. The function T 1→2(ω, L) corresponds to the spectral transmissivity in radiative transfer between media 1 and 2 with a separation of L and is expressed as53
where \({\tilde{R}}_{h1}^{(\mu )}\) and \({\tilde{R}}_{h2}^{(\mu )}\) are polarized effective reflection coefficients of the two half spaces (calculated in the absence of other half space), μ = TE (or TM) refers to transverse electric (or magnetic) polarization and k hz is the z-component of wavevector in vacuum. Here, j is the imaginary unit. For a structure having N-layer media having (N − 1) interfaces, by solving the boundary conditions at the interfaces, one can obtain the expression for the generalized reflection coefficient at the interface between regions i and i + 154,
where \({R}_{i,i+1}^{(\mu )}\) is the Fresnel reflection coefficient at the interface between the layers i and i + 1, and \({\tilde{R}}_{i+\mathrm{1,}i+2}^{(\mu )}\) is the generalized reflection coefficient at the interface between the layers i + 1 and i + 2, z = −d i is the location of the ith interface. \({k}_{i,z}=\sqrt{{\varepsilon }_{i}(\omega ){\omega }^{2}/{c}^{2}-{k}_{\rho }^{2}}\) is the normal z-component of the wave vector in medium i, wherein ε i (ω) is the relative permittivity of the medium i as a function of angular frequency ω, c is the speed of light in vacuum and k ρ is the magnitude of the in-plane wave vector. With \({\tilde{R}}_{N,N+1}^{(\mu )}=0\), the above equation provides a recursive relation to calculate the reflection coefficients \({\tilde{R}}_{i,i+1}^{(\mu )}\) in all regions. Note that Eq. 2 has only one integral corresponding to propagating waves. The terms due to evanescent waves are ignored as separation between the two half spaces is much larger than the thermal wavelength (\(L\gg {\lambda }_{th}\)). The hemispherical emissivity of the active component can be expressed as32
Note that the term for tranmissivity has been omitted as a layer of gold makes the structure opaque.
Insulating VO 2 (below 341 K) is anisotropic. In a plane (x − y plane in Fig. 1) perpendicular to optical axis known as the ordinary mode, its dielectric function is ε O and it is ε E along the optical axis (extraordinary mode). Both ε O and ε E can be calculated using the classical oscillator formula \(\varepsilon (\omega )={\varepsilon }_{\infty }+{\sum }_{i=1}^{N}\frac{{S}_{i}{\omega }_{i}^{2}}{{\omega }_{i}^{2}-j{\gamma }_{i}\omega -{\omega }^{2}}\). Values of high-frequency constant ε ∞, phonon frequency ω i , scattering rate γ i and oscillator strength S i are taken from ref. 55. There are eight phonon modes for ordinary and nine phonon modes for extraordinary dielectric function. In the metallic state, VO2 is isotropic and Drude model55 is used to describe the dielectric function i.e., \(\varepsilon (\omega )=\frac{-{\omega }_{p}^{2}{\varepsilon }_{\infty }}{{\omega }^{2}-j\omega {\rm{\Gamma }}}\). Refractive indices of KBr are taken from ref. 56, while dielectric properties of gold can be found in ref. 57. Blackbody is assumed to have a constant dielectric function ε = 1 + 0.001j.
References
Li, B., Wang, L. & Casati, G. Thermal diode: Rectification of heat flux. Physical review letters 93, 184301 (2004).
Li, B., Wang, L. & Casati, G. Negative differential thermal resistance and thermal transistor. Applied Physics Letters 88, 143501 (2006).
Wang, L. & Li, B. Thermal memory: a storage of phononic information. Physical review letters 101, 267203 (2008).
Kobayashi, W., Teraoka, Y. & Terasaki, I. An oxide thermal rectifier. Applied Physics Letters 95, 171905 (2009).
Sawaki, D., Kobayashi, W., Moritomo, Y. & Terasaki, I. Thermal rectification in bulk materials with asymmetric shape. arXiv preprint arXiv:1102.4182 (2011).
Kobayashi, W. et al. Thermal rectification in the vicinity of a structural phase transition. Applied Physics Express 5, 027302 (2012).
Chang, C., Okawa, D., Majumdar, A. & Zettl, A. Solid-state thermal rectifier. Science 314, 1121–1124 (2006).
Martnez-Pérez, M. J., Fornieri, A. & Giazotto, F. Rectification of electronic heat current by a hybrid thermal diode. Nature nanotechnology 10, 303–307 (2015).
Ben-Abdallah, P. & Biehs, S.-A. Near-field thermal transistor. Physical review letters 112, 044301 (2014).
Ben-Abdallah, P. & Biehs, S.-A. Phase-change radiative thermal diode. Applied Physics Letters 103, 191907 (2013).
Otey, C. R., Lau, W. T. & Fan, S. Thermal rectification through vacuum. Physical Review Letters 104, 154301 (2010).
Chen, Z. et al. A photon thermal diode. Nature communications 5 (2014).
Wang, L. & Li, B. Phononics gets hot. Phys. World 21, 27–29 (2008).
Wang, L. & Li, B. Thermal logic gates: computation with phonons. Physical review letters 99, 177208 (2007).
Ben-Abdallah, P. & Biehs, S.-A. Towards boolean operations with thermal photons. Physical Review B 94, 241401 (2016).
Li, N. et al. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Reviews of Modern Physics 84, 1045 (2012).
Song, B., Fiorino, A., Meyhofer, E. & Reddy, P. Near-field radiative thermal transport: From theory to experiment. AIP Advances 5, 053503 (2015).
Yang, Y., Basu, S. & Wang, L. Radiation-based near-field thermal rectification with phase transition materials. Applied Physics Letters 103, 163101 (2013).
Huang, J., Li, Q., Zheng, Z. & Xuan, Y. Thermal rectification based on thermochromic materials. International Journal of Heat and Mass Transfer 67, 575–580 (2013).
Nefzaoui, E., Joulain, K., Drevillon, J. & Ezzahri, Y. Radiative thermal rectification using superconducting materials. Applied Physics Letters 104, 103905 (2014).
Joulain, K., Ezzahri, Y., Drevillon, J. & Ben-Abdallah, P. Modulation and amplification of radiative far field heat transfer: Towards a simple radiative thermal transistor. Applied Physics Letters 106, 133505 (2015).
Van Zwol, P., Joulain, K., Ben-Abdallah, P., Greffet, J.-J. & Chevrier, J. Fast nanoscale heat-flux modulation with phase-change materials. Physical Review B 83, 201404 (2011).
Van Zwol, P., Ranno, L. & Chevrier, J. Tuning near field radiative heat flux through surface excitations with a metal insulator transition. Physical review letters 108, 234301 (2012).
Menges, F. et al. Thermal radiative near field transport between vanadium dioxide and silicon oxide across the metal insulator transition. Applied Physics Letters 108, 171904 (2016).
Ghanekar, A., Ji, J. & Zheng, Y. High-rectification near-field thermal diode using phase change periodic nanostructure. Applied Physics Letters 109, 123106 (2016).
Yang, Y., Basu, S. & Wang, L. Vacuum thermal switch made of phase transition materials considering thin film and substrate effects. Journal of Quantitative Spectroscopy and Radiative Transfer 158, 69–77 (2015).
Prod’homme, H., Ordonez-Miranda, J., Ezzahri, Y., Drevillon, J. & Joulain, K. Optimized thermal amplification in a radiative transistor. Journal of Applied Physics 119, 194502 (2016).
Zhu, L., Otey, C. R. & Fan, S. Negative differential thermal conductance through vacuum. Applied Physics Letters 100, 044104 (2012).
Lee, K.-T., Ji, C. & Guo, L. J. Wide-angle, polarization-independent ultrathin broadband visible absorbers. Applied Physics Letters 108, 031107 (2016).
Zheng, Y. & Ghanekar, A. Radiative energy and momentum transfer for various spherical shapes: A single sphere, a bubble, a spherical shell, and a coated sphere. Journal of Applied Physics 117, 064314 (2015).
Zhu, L., Otey, C. R. & Fan, S. Ultrahigh-contrast and large-bandwidth thermal rectification in near-field electromagnetic thermal transfer between nanoparticles. Physical Review B 88, 184301 (2013).
Ghanekar, A., Lin, L., Su, J., Sun, H. & Zheng, Y. Role of nanoparticles in wavelength selectivity of multilayered structures in the far-field and near-field regimes. Optics Express 23, A1129–A1139 (2015).
Ghanekar, A., Lin, L. & Zheng, Y. Novel and efficient mie-metamaterial thermal emitter for thermophotovoltaic systems. Optics express 24, A868–A877 (2016).
Rinnerbauer, V. et al. Metallic photonic crystal absorber-emitter for efficient spectral control in high-temperature solar thermophotovoltaics. Advanced Energy Materials 4 (2014).
Chou, J. B. et al. Design of wide-angle selective absorbers/emitters with dielectric filled metallic photonic crystals for energy applications. Optics express 22, A144–A154 (2014).
Biehs, S.-A., Rosa, F. S. & Ben-Abdallah, P. Modulation of near-field heat transfer between two gratings. Applied Physics Letters 98, 243102 (2011).
Zheludev, N. I. & Kivshar, Y. S. From metamaterials to metadevices. Nature materials 11, 917–924 (2012).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nature materials 13, 139–150 (2014).
Ünlü, M. S. & Strite, S. Resonant cavity enhanced photonic devices. Journal of Applied Physics 78, 607–639 (1995).
Kishino, K. et al. Resonant cavity-enhanced (rce) photodetectors. IEEE Journal of Quantum Electronics 27, 2025–2034 (1991).
Fante, R. L. & Mccormack, M. T. Reflection properties of the salisbury screen. IEEE transactions on antennas and propagation 36, 1443–1454 (1988).
Ra ÄôDi, Y., Simovski, C. & Tretyakov, S. Thin perfect absorbers for electromagnetic waves: theory, design, and realizations. Physical Review Applied 3, 037001 (2015).
Bosman, H., Lau, Y. & Gilgenbach, R. Microwave absorption on a thin film. Applied Physics Letters 82, 1353–1355 (2003).
Hägglund, C., Apell, S. P. & Kasemo, B. Maximized optical absorption in ultrathin films and its application to plasmon-based two-dimensional photovoltaics. Nano letters 10, 3135–3141 (2010).
Pu, M. et al. Ultrathin broadband nearly perfect absorber with symmetrical coherent illumination. Optics express 20, 2246–2254 (2012).
Nefzaoui, E., Drevillon, J., Ezzahri, Y. & Joulain, K. Simple far-field radiative thermal rectifier using fabry–perot cavities based infrared selective emitters. Applied optics 53, 3479–3485 (2014).
Kats, M. A. et al. Ultra-thin perfect absorber employing a tunable phase change material. Applied Physics Letters 101, 221101 (2012).
Taylor, S., Yang, Y. & Wang, L. Vanadium dioxide based fabry-perot emitter for dynamic radiative cooling applications. Journal of Quantitative Spectroscopy and Radiative Transfer (2017).
Qazilbash, M. et al. Infrared spectroscopy and nano-imaging of the insulator-to-metal transition in vanadium dioxide. Physical Review B 79, 075107 (2009).
Frenzel, A. et al. Inhomogeneous electronic state near the insulator-to-metal transition in the correlated oxide vol 2. Physical Review B 80, 115115 (2009).
Ordonez-Miranda, J., Ezzahri, Y., Drevillon, J. & Joulain, K. Transistorlike device for heating and cooling based on the thermal hysteresis of vol 2. Physical Review Applied 6, 054003 (2016).
Kats, M. A. & Capasso, F. Optical absorbers based on strong interference in ultra-thin films (laser photonics rev. 10 (5)/2016). Laser & Photonics Reviews 10, 699–699 (2016).
Narayanaswamy, A. & Zheng, Y. A Green’s function formalism of energy and momentum transfer in fluctuational electrodynamics. Journal of Quantitative Spectroscopy and Radiative Transfer 132, 12–21 (2014).
Chew, W. C. Waves and fields in inhomogeneous media (IEEE press, 1995).
Barker, A. Jr, Verleur, H. & Guggenheim, H. Infrared optical properties of vanadium dioxide above and below the transition temperature. Physical Review Letters 17, 1286 (1966).
Li, H. Refractive index of alkali halides and its wavelength and temperature derivatives. Journal of physical and chemical reference data 5, 329–528 (1976).
Johnson, P. B. & Christy, R.-W. Optical constants of the noble metals. Physical Review B 6, 4370 (1972).
Acknowledgements
This project was supported in part by an Institutional Development Award (IDeA) Network for Biomedical Research Excellence from the National Institute of General Medical Sciences of the National Institutes of Health under grant number P20GM103430, the National Center for Research Resources/Center of Biological Research Excellence of the National Institutes of Health under grant number 5P30GM110759, Rhode Island STAC Research Grant number AWD05085, and Rhode Island Fundation Research Grant number 20164342. Work at Brown University was supported by National Science Foundation through Grant number DMR-1307056.
Author information
Authors and Affiliations
Contributions
A.G. did the calculations for far-field thermal diode. G.X. provided technical insights of physical phenomena. Y.Z. supervised the project. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghanekar, A., Xiao, G. & Zheng, Y. High Contrast Far-Field Radiative Thermal Diode. Sci Rep 7, 6339 (2017). https://doi.org/10.1038/s41598-017-06804-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-06804-w
This article is cited by
-
Effect of the Filling Liquid Ratio on the Thermal Performance of a Novel Thermal Diode with Wick
Journal of Thermal Science (2024)
-
Enhancement of passive daytime radiative cooling performance with a novel hybrid strategy of integrating double-layer nanoparticle-based coating and ballistic thermal rectifier
Journal of Thermal Analysis and Calorimetry (2023)
-
Adaptive tuning of infrared emission using VO2 thin films
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.