Abstract
The purpose of this study is to conduct modeling and simulation to understand the effect of shock-induced mechanical loading, in the form of cavitation bubble collapse, on damage to the brain’s perineuronal nets (PNNs). It is known that high-energy implosion due to cavitation collapse is responsible for corrosion or surface damage in many mechanical devices. In this case, cavitation refers to the bubble created by pressure drop. The presence of a similar damage mechanism in biophysical systems has long being suspected but not well-explored. In this paper, we use reactive molecular dynamics (MD) to simulate the scenario of a shock wave induced cavitation collapse within the perineuronal net (PNN), which is the near-neuron domain of a brain’s extracellular matrix (ECM). Our model is focused on the damage in hyaluronan (HA), which is the main structural component of PNN. We have investigated the roles of cavitation bubble location, shockwave intensity and the size of a cavitation bubble on the structural evolution of PNN. Simulation results show that the localized supersonic water hammer created by an asymmetrical bubble collapse may break the hyaluronan. As such, the current study advances current knowledge and understanding of the connection between PNN damage and neurodegenerative disorders.
Similar content being viewed by others
Introduction
Cavitation is the term defined by bubbles that are created when pressure is dropped below saturated vapor pressure. In principle, cavitation-induced bubbles are unstable in nature, that is, as soon as the pressure is reinstated above vapor pressure, bubbles immediately collapse. The high-energy jet produced during cavitation collapse often causes surface damage to many high-speed machines, such as underwater propeller blades. Recently, a series of studies have been conducted focusing on a similar damage mechanism of collapsing nanobubbles in the biophysical systems1, 2, especially in the most delicate system—the human brain3,4,5.
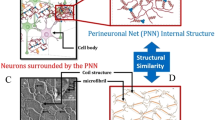
A blast from an explosive device may lead to traumatic brain injury (TBI)6, and the level of injury can range from a mild concussion to a severe penetrating injury. Recent studies on animal models suggest that mild TBI7,8,9 is directly connected with the later appearance of progressive neurodegenerative disorders such as Alzheimer’s disease (AD)10,11,12,13 and chronic traumatic encephalopathy (CTE)14 as well as posttraumatic stress disorder (PTSD)15,16,17,18. Under a blast, the brain suffers from a highly dynamic mechanical force, and, in principle, pressure in some portion of the brain’s fluid system may become low enough to induce cavitation. Until now, most experimental studies mimicking blast-like scenarios are observed via optical microscopy, which are limited by the device resolution being 1 μm or higher2, 8, 19,20,21. Of these studies, only a handful of studies have been reported on how different micro-scale brain components, such as cell membranes (lipid bilayers)2, 22,23,24,25,26,27,28,29, ion channel30, and blood-brain barrier31, 32, respond to impact caused by cavitation bubble collapse. While these studies explored various components of the brain when subjected to a shock-wave and cavitation collapse, little is known about the role of a shock-wave on the morphological evolution of a brain’s extracellular matrix (ECM)19. Animal studies suggest that many neurodegenerative disorders are associated with the pathological changes of the ECM that primarily surrounds the neuron cells (Fig. 1a)33,34,35,36,37. The area of ECM surrounding the neurons is known as a perineuronal net (PNN)11, 12, 38,39,40,41,42. Structurally, the PNN is primarily composed of water, free ions and three major types of biomolecules: hyaluronan (HA), tenascins, and lecticans (Fig. 1b)37, 43. From a physiological standpoint, pathological changes of PNN would imply degeneration or transformation of its biomolecular constituents.
(a) Neurons surrounded by the ECM in the CNS. The region in ECM in the immediate vicinities of neurons are called Perinuronal Net (PNN). The components of PNN are shown in the magnified view (adapted from Fig. 1 of 37) (Permitted reprint) and (b–d) Schematic of pre-, during, and post-collapse bubble.
While it is not clearly known what level of applied shock on a PNN will lead to the formation and collapse of a cavitional bubble, it is known that the nanobubbles are generally unstable, and surface tension at the nanometer scale is a critical factor. Based on the Young-Laplace law44, the Laplace pressure from surface tension inversely scales with the bubble size45, 46. At the nanometer scale, when a bubble containing fluid is impacted by a traveling wave, the local fluctuation of pressure in the fluid combined with surface tension significantly increases the collapsing possibility of nanobubbles. During collapse, liquid surrounding a bubble is driven toward the center of the bubble resulting in the conversion of potential energy to kinetic energy. If the bubble collapse is asymmetrical47, then it may induce a high-velocity jet, referred as “water hammer (WH)”. A WH is characterized by its one-direction flow pattern and has the potential to cause damage to materials coming its way. Asymmetrical collapse can occur based on two possible scenarios. The first scenario is associated with the “Rayleigh collapse” where the cavitation-bubble collapses under a uniformly reinstated pressure near a solid surface to guide the water hammer toward the solid surface. The second scenario is connected to a shockwave induced bubble collapse where the water hammer is formed and travels along the shockwave propagating direction48. In both scenarios, the pressure difference drives the water hammer. In the Rayleigh collapse, the pressure difference exists between the inside and outside of the bubble. For shock-induced collapse, the pressure difference is created due to variation between the post-shock pressure and the bubble pressure. It can be argued that, in principle, blast-induced shock can cause formation and collapse of cavitation bubbles in PNN, and the resulting jet produced near the collapsing nanobubbles can become high enough to cause pathological changes of PNN.
In this paper, fully atomistic simulations were used to interrelate applied shock, water-hammer kinetics and damage mechanisms in PNN. We investigated whether water hammer is even capable of breaking the HA. A study on the effect of cavitation bubble size on HA damage is also presented. To investigate these issues, we used reactive molecular dynamics simulation (reaxFF potential)49, 50 to model the events occurring at the nanometer scale and sub-nanosecond time frame. While conventional molecular dynamics simulation can capture events like bubble ripening51,52,53 and collapse23, 24, 30, 31, 54,55,56,57,58 in homogenous fluids, the use of reactive molecular dynamics is essential to the assessment of PNN damage because of PNN’s heterogeneous morphology. The simulation results demonstrate the possible shock-induced damage mechanisms of HA due to bubble collapse.
Simulation Methods
Our model consists of three major components: Hyaluronan (HA), surrounding water, and ions. The initial molecular structure of HA is obtained from prior molecular dynamics simulation suggesting that a stable periodic formation of HA is a four-fold helix59. Since the available profile of HA only has the acidic part, i.e. the biomolecule in water is not electronically neutral, for each simulation, we had to balance the “extra” charges with counter ions. Here we used a matching number of H ions (H+) as counter-ions located 4 nm away from the symmetric axis (5 for each fold, 1 for the end node). The size of the simulation box is approximately 16 nm by 16 nm by 25 nm containing 599,205 atoms in total with a 12-fold hyaluronan (~500 atoms). Once the model was developed, we equilibrated the whole system at 300 K (26.85 °C) and 101 kPa pressure (Appendix 1 has more detail on the simulation set-up). We used Nose-Hoover’s barostat (piston) and thermostat (heater). The time constants for the piston was set at 1 ps and the heater was set at 50 fs.
Our simulations were aimed to quantify the impact of bubble collapse triggered by a shock wave (Fig. 1d). To create a “cavitation-induced bubble,” we manually removed a water sphere from the original simulation box. The artificially created vacuum is slightly different from the naturally formed cavitation-induced bubble in that a naturally formed bubble contains gas molecules inside. In our prior simulations (Appendix 2), we found that a cavitation bubble encloses only low-pressure gas. Therefore, we determined that the number of gas molecules inside the bubble are too few to affect the shock collapse process. We considered three different bubble diameters, 5 nm, 8 nm, and 10 nm. One model was also built without a bubble. We generated shock from the positive z-direction toward the negative z-direction using the reflective boundary condition method56, 60 (Appendix 1 describes the shock generation method). Shock propagation and bubble collapse were simulated with an NVE ensemble. The z-direction was selected as the shock propagating direction. Reflective boundary condition is applied in boundaries normal to z direction. The other two boundaries (normal to x and y direction) are modeled as periodic. The shock front travels such that it first encounters the cavitation bubble. As the bubble collapses, the traveling shock front then hits the HA with the collapse-induced WH. In this paper, we have considered initial “piston” velocity (post shock particle velocity) v p as 1 km/s, 2 km/s and 3 km/s, which translates to shock velocity v s 3.6 km/s, 5.35 km/s and 7.2 km/s, respectively.
By subjecting the four distinct models (i.e. models with three different bubble sizes plus the one without a bubble in PNN) with three different shock wave velocities, we performed simulations under 12 different scenarios. Three independent sets of simulations for each scenario (total 36 sets) were conducted to eliminate any significant statistical disparity. The initial orientation of the HA molecule along with its axis is the only factor that varied in the three sets of simulations. The HA was rotated 90 degrees around its length axis for each set before the equilibration. We recognize that the size of the bubbles is limited based on the nm length scale. Prior research61,62,63 shows surface or bulk bubble of a few tens of nanometers were stable for a few hours. Unfortunately, the computational cost for high fidelity MD simulation using reactive potential on systems with the “larger” bubble is very high and beyond the scope of current effort.
Maximum over-pressure generated from an explosive blast is ~1 MPa. Since we are simulating bubbles that are about 10 times smaller than the experimentally observed stable nanobubbles, we chose the shock velocities related to a similar amount of WH kinetic energy. The total water-hammer-jet kinetic energy is related to the bubble size and the post-shock pressure of an ideal planar shock wave through:
where E k , D, and p p are the total kinetic energy of the water hammer, diameter of the bubble, and post-shock pressure, respectively. It is apparent that we need to have p p to be 1000 times stronger than 1 MPa (i.e. ~1 GPa) to remain consistent with the microscopic bubble (10 times larger than what we used) collapse.
The interatomic and intermolecular interactions for the entire system, including HA, water, and counter ions, have been prescribed by high-fidelity but computationally expensive ReaxFF potential49. Unlike conventional interatomic potential where chemically bonded interatomic interactions are estimated based on a predefined potential function, the ReaxFF potential determines interatomic bonding as the outcome of atom position at each time step, which makes it capable of simulating bond breaking and building. The use of ReaxFF in our simulation was essential for assessing the damage to molecules such as HA that actively interact with surrounding water molecules and ions. All of our simulation were conducted on LAMMPS64. Post-processing and visualization of data were conducted using MATLAB65 and Ovito66, respectively.
Results and Discussion
The bubble collapse process and the subsequent effect on the HA is shown in Fig. 2. The mechanism of bubble collapse agrees well with many existing simulation studies23,24,25, 30, 31, 55, 56, 60. It can be inferred from Fig. 2 that when a shockwave passes through the cavitation bubble, the post-shock pressure gradually compresses the anterior side of the bubble. Since the density of a bubble’s interior is far less than the surrounding bulk liquid, the post-shock pressure leads to faster bubble collapsing speed with a magnitude even faster than the shockwave. Subsequently, the collapsing jet (WH jet) strongly collides with the other side of the bubble. It can be inferred that larger bubble collisions create stronger WH jets, which hold larger kinetic energy. Such a WH jet takes longer to dissipate after the collision. Once the WH jet lands on the HA, the HA starts to deform and continues to deform until the WH jet completely passes through it. The GIF animation of bubble collapse, velocity contour, pressure contour, and density contour can be found online as Supporting Material.
Depending on bubble size and initial shock-speed, HA’s structural evolutions inside PNN can be described either by (a) large-scale deformation or (b) complete rupture, as shown in Fig. 3(a). In Fig. 3, the “arrow” used to indicate the WH jet direction is marked in blue if the HA is intact. For an HA broken by a cavitation collapse, the “arrow” is marked in red. The five cases where HA was broken were due to the presence of larger bubbles and faster shockwave velocities. For a 10-nm bubble case, the rupture can even happen in multiple sites. It can be hypothesized that HA has no time to release the stress when moving along the axial direction. In other cases, the HA is seen to sustain bending-like large deformation but remains intact. In those cases, the HA can stretch its helical structure to avoid breaking.
The local bonding evolution in the form of chemical, hydrogen and the van der Waals bonding of HA is revealed in Fig. 3(b,c). Three major events can be observed. First, due to the acidic nature, HA keeps building and losing hydrogen bonds with the surrounding water molecules. There is no significant increase or decrease of hydrogen bonding before and after shock and jet stream. Second, a strong jet stream can rupture the HA into two or more pieces. As shown in Fig. 3c, the first breaking point of HA involves breaking of a glucoside bond. In this case, the “intact” segments of HA do not exhibit major structural change. In the last scenario, the glucose ring structure in HA can also be broken during jet impact.
To discuss the damage mechanism of HA further, we picked up the systems with 5 nm and 10 nm bubbles that are subjected to the same shock velocity of 5.35 km/s. We divided the simulation cell into small cubic bins (each bin has a side length = 1 nm) and evaluated the continuum properties inside. We chose the 5 nm and 10 nm bubble diameters because same shock velocity on 5 nm and 10 nm bubbles yielded two different outcomes—one breaks the HA and the other does not. It is interesting to observe that in the case of a 5 nm bubble, the max velocity drops much quicker compared to the case of a 10 nm bubble. The local velocity profile can be found in Fig. 4. As shown in Fig. 4(a), as soon as the bubble starts to collapse, the maximum local velocity raises, and then it starts to drop once the jet hits the other side of the bubble. Figure 4(d) shows the case of a 10 nm bubble where WH ruptures HA. It can be observed that WH velocities near the center and the ending of HA differ by ~2.5 km/s. No velocity difference is observed when no bubble is present (Fig. 4(b)). The velocity difference is less than 1 km/s when bubble size is 5 nm, as can be seen in Fig. 4(c). At any particular instant of time (e.g. 6 ps, 6.5 ps or 7 ps) and at any particular point “x” (0 nm ≤ × ≤ 15 nm), local fluid velocities vary among the three simulation sets. Error bars at each data point indicate the standard deviation. We believe two factors have played role in local velocity variation. One is due to the local dynamics of individual atoms. Since local fluid velocities at any location are calculated from the sum of atomic velocities, the stochastic nature of atomic velocities is reflected in the local velocity estimation. The relative variations in local velocities are also believed to be influenced by the axial orientation of HA relative to the oncoming shock front. Since we rotated HA about its own axis by 90 degrees when we build model for simulation set 2, and then by another 90 degrees (i.e. 180 degree rotation compared to the orientation in set 1) in simulation set 3, the shortest distances between the HA and the bubble surface slightly change, as shown in Fig. 5. Such changes in distance implies shock front lands on HA at slightly different time. However, we report local velocities at a particular instant of time only. As such, local velocities in different simulation set very at the beginning (i.e. at 6 ps). It can be noticed that the degree of deviation reduces once the HA is fully in the thrust zone. It can also be observed that the overall trends in local velocity profiles are very consistent confirming our simulation outcome is reproducible.
For shock velocity of 3.6 km/s, (a) graphs the maximum local velocity profile with time, and (b–d) graphs the local velocity along the HA axis. The local velocity has been computed by taking average velocities of atoms inside a cubic bin where side equals 1 nm. Error bar shows the relative local velocity variation based on the three simulations conducted with the same bubble size and the same applied shock velocity.
(a) Equilibrated MD snapshots showing the variation in the distance between HA and bubble surface caused by the change in HA’s axial orientation. Note that the axial orientation of HA varied by 90 degrees between the three sets of simulation. (b–d) Magnified MD snapshots of the HA in set 1, 2 and 3. The atoms are colored as: white for H, black for C, blue for N, red for O.
It is shown in Eqn. (1), the total water-hammer-jet kinetic energy is roughly proportional to the bubble size and the post-shock pressure. Since the Kinect energy disperses in the radial direction after the impact (see Fig. 1(d)), the averaged kinetic energy per frontal area that acts on the HA can be estimated by
where d is the distance between the bubble and the HA. We have listed the “estimated” kinetic energy per frontal area for all nine cases (having a bubble) of our simulation in Table 1 using d = 1 nm. We regard this kinetic energy as “estimated” because the post-shock pressure was “estimated” based on spaced-averaged (post-shock area) simulation data obtained during the equilibration phase of our simulation. The magnitude of the pressure value will vary if someone space-averages the pressure value at different instant of time. As such, the data in Table 1 should be taken as a guideline for obtaining first-order estimated kinetic energy threshold to break the HA. Nevertheless, it can be inferred from Table 1 that the HA can break when energy exceeds 40 N/m.
For all simulations, the evolution of the molecular composition of HA and ions were monitored. We observe that bubble collapse does not induce significant composition change to the HA (except the rupture). Also, the ion count was not affected by the collision.
Conclusions
By observing how the HA suffered from the water-hammer, it is obvious that the local damaging of the PNN was largely enhanced by the jet formed during bubble collapse. This is further corroborated from the case with no bubble where we found that even a high-velocity shockwave was not enough to break the HA. Thus, we conclude the following
-
The results of the research presented herein suggest that larger the bubble size, the bigger the impact is on the HA. Unfortunately, the computational cost for the reactive MD is excessively high (a large memory is required). As such, bubbles larger than 10 nm were not tested in this study. The critical size of a bubble that is able to break HA with minimal pressure drop (post-shock and bubble pressure in this case) is still unknown.
-
The estimation method of kinetic energy per frontal area gives a rough guideline for estimating the energy that is required to break HA. The estimation method developed in this research worked for the nine cases tested.
The link between blast induced Traumatic Brain Injury (TBI) with the PNN through the cavitation collapse is a very interesting research direction that can possibly relate to the symptoms of PTSD. If the HA can be broken by a nanobubble collapse, it is highly possible that a blast can disassemble the PNN. More studies on this possibility are underway.
References
Husseini, G. A., Pitt, W. G. & Martins, A. M. Ultrasonically triggered drug delivery: breaking the barrier. Colloids and Surfaces B: Biointerfaces 123, 364–386 (2014).
Mager, M. D. & Melosh, N. A. Lipid bilayer deposition and patterning via air bubble collapse. Langmuir 23, 9369–9377 (2007).
Kurosawa, Y. et al. In Engineering in Medicine and Biology Society, 2009. EMBC 2009. Annual International Conference of the IEEE. 7224–7227 (IEEE).
Goeller, J., Wardlaw, A., Treichler, D., O’Bruba, J. & Weiss, G. Investigation of cavitation as a possible damage mechanism in blast-induced traumatic brain injury. Journal of neurotrauma 29, 1970–1981 (2012).
Nakagawa, A. et al. Mechanisms of primary blast-induced traumatic brain injury: insights from shock-wave research. Journal of neurotrauma 28, 1101–1119 (2011).
Taber, K. H., Warden, D. L. & Hurley, R. A. Blast-related traumatic brain injury: what is known? The Journal of neuropsychiatry and clinical neurosciences 18, 141–145 (2006).
Arciniegas, D. B., Anderson, C. A., Topkoff, J. & McAllister, T. W. Mild traumatic brain injury: a neuropsychiatric approach to diagnosis, evaluation, and treatment. Neuropsychiatric disease and treatment 1, 311 (2005).
Sosa, M. A. G. et al. Blast overpressure induces shear-related injuries in the brain of rats exposed to a mild traumatic brain injury. Acta neuropathologica communications 1, 1 (2013).
Kamnaksh, A. et al. Neurobehavioral, cellular, and molecular consequences of single and multiple mild blast exposure. Electrophoresis 33, 3680–3692 (2012).
Sivanandam, T. M. & Thakur, M. K. Traumatic brain injury: a risk factor for Alzheimer’s disease. Neuroscience & Biobehavioral Reviews 36, 1376–1381 (2012).
Morawski, M., Brückner, G., Jäger, C., Seeger, G. & Arendt, T. Neurons associated with aggrecan-based perineuronal nets are protected against tau pathology in subcortical regions in Alzheimer’s disease. Neuroscience 169, 1347–1363 (2010).
Lepelletier, F. X., Mann, D., Robinson, A., Pinteaux, E. & Boutin, H. Early changes in extracellular matrix in Alzheimer’s disease. Neuropathology and applied neurobiology (2015).
Emmerling, M. et al. Traumatic brain injury elevates the Alzheimer’s amyloid peptide Aβ42 in human CSF: a possible role for nerve cell injury. Annals of the New York Academy of Sciences 903, 118–122 (2000).
Omalu, B. I., Hamilton, R. L., Kamboh, M. I., DeKosky, S. T. & Bailes, J. Chronic traumatic encephalopathy (CTE) in a National Football League Player: Case report and emerging medicolegal practice questions. Journal of forensic nursing 6, 40–46 (2010).
Campbell, T. A. et al. Neuropsychological measures of processing speed and executive functioning in combat veterans with PTSD, TBI, and comorbid TBI/PTSD. Psychiatric Annals 39 (2009).
Gogolla, N., Caroni, P., Lüthi, A. & Herry, C. Perineuronal nets protect fear memories from erasure. Science 325, 1258–1261 (2009).
Tsien, R. Y. Very long-term memories may be stored in the pattern of holes in the perineuronal net. Proceedings of the National Academy of Sciences 110, 12456–12461 (2013).
Genovese, R. F. et al. Effects of mild TBI from repeated blast overpressure on the expression and extinction of conditioned fear in rats. Neuroscience 254, 120–129 (2013).
Bar-Kochba, E., Scimone, M. T., Estrada, J. B. & Franck, C. Strain and rate-dependent neuronal injury in a 3D in vitro compression model of traumatic brain injury. Scientific Reports 6 (2016).
Chen, Y. C., Smith, D. H. & Meaney, D. F. In-vitro approaches for studying blast-induced traumatic brain injury. Journal of neurotrauma 26, 861–876 (2009).
Hong, Y., Sarntinoranont, M., Subhash, G., Canchi, S. & King, M. Localized Tissue Surrogate Deformation due to Controlled Single Bubble Cavitation. Experimental Mechanics, 1–13 (2014).
Sliozberg, Y. & Chantawansri, T. Damage in spherical cellular membrane generated by the shock waves: Coarse-grained molecular dynamics simulation of lipid vesicle. The Journal of Chemical Physics 141, 184904 (2014).
Adhikari, U., Goliaei, A. & Berkowitz, M. L. Mechanism of Membrane Poration by Shock Wave Induced Nanobubble Collapse: A Molecular Dynamics Study. The Journal of Physical Chemistry B 119, 6225–6234 (2015).
Santo, K. P. & Berkowitz, M. L. Shock wave interaction with a phospholipid membrane: coarse-grained computer simulations. The Journal of Chemical Physics 140, 054906 (2014).
Choubey, A. et al. Poration of lipid bilayers by shock-induced nanobubble collapse. Applied Physics Letters 98, 023701 (2011).
Koshiyama, K., Kodama, T., Yano, T. & Fujikawa, S. Molecular dynamics simulation of structural changes of lipid bilayers induced by shock waves: Effects of incident angles. Biochimica et Biophysica Acta (BBA)-Biomembranes 1778, 1423–1428 (2008).
Fu, H., Comer, J., Cai, W. & Chipot, C. Sonoporation at small and large length scales: effect of cavitation bubble collapse on membranes. The journal of physical chemistry letters 6, 413–418 (2015).
Ganzenmüller, G., Hiermaier, S. & Steinhauser, M. Shock-wave induced damage in lipid bilayers: a dissipative particle dynamics simulation study. Soft Matter 7, 4307–4317 (2011).
Koshiyama, K., Kodama, T., Yano, T. & Fujikawa, S. Structural change in lipid bilayers and water penetration induced by shock waves: molecular dynamics simulations. Biophysical journal 91, 2198–2205 (2006).
Lau, E. Y., Berkowitz, M. L. & Schwegler, E. Shock Wave-Induced Damage of a Protein by Void Collapse. Biophysical journal 110, 147–156 (2016).
Goliaei, A., Adhikari, U. & Berkowitz, M. L. Opening of the Blood-Brain Barrier Tight Junction Due to Shock Wave Induced Bubble Collapse: A Molecular Dynamics Simulation Study. ACS chemical neuroscience 6, 1296–1301 (2015).
Reneer, D. V. Blast-induced brain injury: Influence of shockwave components (2012).
Laywell, E. D. et al. Enhanced expression of the developmentally regulated extracellular matrix molecule tenascin following adult brain injury. Proceedings of the National Academy of Sciences 89, 2634–2638 (1992).
Burnside, E. & Bradbury, E. Review: manipulating the extracellular matrix and its role in brain and spinal cord plasticity and repair. Neuropathology and applied neurobiology 40, 26–59 (2014).
Morawski, M., Filippov, M., Tzinia, A., Tsilibary, E. & Vargova, L. ECM in brain aging and dementia. Prog. Brain Res 214, 207–227 (2014).
Bonneh‐Barkay, D. & Wiley, C. A. Brain extracellular matrix in neurodegeneration. Brain pathology 19, 573–585 (2009).
Lau, L. W., Cua, R., Keough, M. B., Haylock-Jacobs, S. & Yong, V. W. Pathophysiology of the brain extracellular matrix: a new target for remyelination. Nature Reviews Neuroscience 14, 722–729 (2013).
Soleman, S., Filippov, M., Dityatev, A. & Fawcett, J. Targeting the neural extracellular matrix in neurological disorders. Neuroscience 253, 194–213 (2013).
Sherman, L. S., Matsumoto, S., Su, W., Srivastava, T. & Back, S. A. Hyaluronan Synthesis, Catabolism, and Signaling in Neurodegenerative Diseases. International journal of cell biology 2015 (2015).
Pantazopoulos, H. & Berretta, S. In Sickness and in Health: Perineuronal Nets and Synaptic Plasticity in Psychiatric Disorders. Neural plasticity 2016 (2015).
Bitanihirwe, B. K. & Woo, T.-U. W. Perineuronal nets and schizophrenia: the importance of neuronal coatings. Neuroscience & Biobehavioral Reviews 45, 85–99 (2014).
Pantazopoulos, H., Woo, T.-U. W., Lim, M. P., Lange, N. & Berretta, S. Extracellular matrix-glial abnormalities in the amygdala and entorhinal cortex of subjects diagnosed with schizophrenia. Archives of general psychiatry 67, 155–166 (2010).
Dzyubenko, E., Gottschling, C. & Faissner, A. Neuron-Glia Interactions in Neural Plasticity: Contributions of Neural Extracellular Matrix and Perineuronal Nets. Neural plasticity 2016 (2016).
Matsumoto, M. & Tanaka, K. Nano bubble—Size dependence of surface tension and inside pressure. Fluid dynamics research 40, 546–553 (2008).
Kudryashov, N. A. & Sinelshchikov, D. I. Analytical solutions for problems of bubble dynamics. Physics Letters A 379, 798–802 (2015).
Mancas, S. C. & Rosu, H. C. Evolution of spherical cavitation bubbles: Parametric and closed-form solutions. Physics of Fluids (1994-present) 28, 022009 (2016).
Johnsen, E. & Colonius, T. Numerical simulations of non-spherical bubble collapse. Journal of fluid mechanics 629, 231–262 (2009).
Magaletti, F., Gallo, M., Marino, L. & Casciola, C. M. Shock-induced collapse of a vapor nanobubble near solid boundaries. International Journal of Multiphase Flow 84, 34–45 (2016).
Monti, S. et al. Exploring the conformational and reactive dynamics of biomolecules in solution using an extended version of the glycine reactive force field. Physical Chemistry Chemical Physics 15, 15062–15077 (2013).
Van Duin, A. C., Dasgupta, S., Lorant, F. & Goddard, W. A. ReaxFF: a reactive force field for hydrocarbons. The Journal of Physical Chemistry A 105, 9396–9409 (2001).
Watanabe, H., Inaoka, H. & Ito, N. Ripening kinetics of bubbles: A molecular dynamics study. The Journal of Chemical Physics 145, 124707 (2016).
Watanabe, H., Suzuki, M., Inaoka, H. & Ito, N. Ostwald ripening in multiple-bubble nuclei. The Journal of Chemical Physics 141, 234703 (2014).
Hoang Viet, M., Derreumaux, P. & Nguyen, P. H. Nonequilibrium all-atom molecular dynamics simulation of the bubble cavitation and application to dissociate amyloid fibrils. The Journal of Chemical Physics 145, 174113 (2016).
Xiao, C., Heyes, D. & Powles, J. The collapsing bubble in a liquid by molecular dynamics simulations. Molecular Physics 100, 3451–3468 (2002).
Nomura, K., Kalia, R., Nakano, A., Vashishta, P. & van Duin, A. Mechanochemistry of shock-induced nanobubble collapse near silica in water. Applied Physics Letters 101, 073108 (2012).
Vedadi, M. et al. Structure and dynamics of shock-induced nanobubble collapse in water. Physical review letters 105, 014503 (2010).
Okumura, H. & Itoh, S. G. Amyloid fibril disruption by ultrasonic cavitation: nonequilibrium molecular dynamics simulations. Journal of the American Chemical Society 136, 10549–10552 (2014).
Okumura, H. & Ito, N. Nonequilibrium molecular dynamics simulations of a bubble. Physical Review E 67, 045301 (2003).
Almond, A., DeAngelis, P. L. & Blundell, C. D. Hyaluronan: the local solution conformation determined by NMR and computer modeling is close to a contracted left-handed 4-fold helix. Journal of molecular biology 358, 1256–1269 (2006).
Shekhar, A., Nomura, K.-i, Kalia, R. K., Nakano, A. & Vashishta, P. Nanobubble collapse on a silica surface in water: Billion-atom reactive molecular dynamics simulations. Physical review letters 111, 184503 (2013).
Ushikubo, F. Y. et al. Evidence of the existence and the stability of nano-bubbles in water. Colloids and Surfaces A: Physicochemical and Engineering Aspects 361, 31–37 (2010).
Peng, H., Birkett, G. R. & Nguyen, A. V. Progress on the Surface Nanobubble Story: What is in the bubble? Why does it exist? Advances in colloid and interface science 222, 573–580 (2015).
White, E. R., Mecklenburg, M., Singer, S. B., Aloni, S. & Regan, B. C. Imaging nanobubbles in water with scanning transmission electron microscopy. Applied Physics Express 4, 055201 (2011).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. Journal of computational physics 117, 1–19 (1995).
Guide, M. Us The mathworks. Inc., Natick, MA 5, 333 (1998).
Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Modelling and Simulation in Materials Science and Engineering 18, 015012 (2009).
Acknowledgements
A.A. acknowledges supports from Office of Naval Research (ONR), Award #N00014-16-1-2142 (Dr. Timothy Bentley, Program Manager). The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported within this paper. URL: http://www.tacc.utexas.edu. A.A. is thankful to Dr. Siddiq Qidwai (former NRL scientist, currently at NSF), Dr. Amit Bagchi (NRL) and Dr. Tom O’Shaughnessy (NRL) for providing helpful information on blast-induced cavitation damage in the brain.
Author information
Authors and Affiliations
Contributions
Y.T.W. and A.A. designed the simulation. Y.T.W. conducted the numerical simulation(s). A.A. and Y.T.W. analyzed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wu, YT., Adnan, A. Effect of Shock-Induced Cavitation Bubble Collapse on the damage in the Simulated Perineuronal Net of the Brain. Sci Rep 7, 5323 (2017). https://doi.org/10.1038/s41598-017-05790-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-05790-3
This article is cited by
-
Effect of air stone pore size and gas flow rate on the recovery efficiency of paclitaxel from biomass in gas bubble-assisted extraction
Korean Journal of Chemical Engineering (2023)
-
On the Molecular Level Cavitation in Soft Gelatin Hydrogel
Scientific Reports (2020)
-
Effects of Focal Axonal Swelling Level on the Action Potential Signal Transmission
Journal of Computational Neuroscience (2020)
-
Effects of Bubble Size and Gas Density on the Shock-induced Collapse of Nanoscale Cavitation Bubble
Multiscale Science and Engineering (2020)
-
Damage and Failure of Axonal Microtubule under Extreme High Strain Rate: An In-Silico Molecular Dynamics Study
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.