Abstract
Accurate prediction of the electronic and hydrogen storage properties of linear carbon chains (C n ) and Li-terminated linear carbon chains (Li2C n ), with n carbon atoms (n = 5–10), has been very challenging for traditional electronic structure methods, due to the presence of strong static correlation effects. To meet the challenge, we study these properties using our newly developed thermally-assisted-occupation density functional theory (TAO-DFT), a very efficient electronic structure method for the study of large systems with strong static correlation effects. Owing to the alteration of the reactivity of C n and Li2C n with n, odd-even oscillations in their electronic properties are found. In contrast to C n , the binding energies of H2 molecules on Li2C n are in (or close to) the ideal binding energy range (about 20 to 40 kJ/mol per H2). In addition, the H2 gravimetric storage capacities of Li2C n are in the range of 10.7 to 17.9 wt%, satisfying the United States Department of Energy (USDOE) ultimate target of 7.5 wt%. On the basis of our results, Li2C n can be high-capacity hydrogen storage materials that can uptake and release hydrogen at temperatures well above the easily achieved temperature of liquid nitrogen.
Similar content being viewed by others
Introduction
Hydrogen (H2), as a pure energy carrier, has many attributes. Being lightweight, it carries 142 MJ/kg of energy, which is approximately three times the energy content of gasoline, in terms of mass. Also, it is highly abundant on the earth in the form of water. More importantly, when hydrogen is burned with oxygen, it releases water vapor as the only effluent. Despite these advantages, there remain several problems to be clarified for the use of hydrogen. For example, hydrogen is highly flammable, and hence, if it comes in contact with the environment, it will burst. Another problem is related to its low energy content in terms of volume: it has only 0.0180 MJ/L, which is very low relative to gasoline (34.8 MJ/L). Moreover, over the past few years, the storage of hydrogen for onboard applications has been an active arena, which also requires a lightweight storage medium. Because of these reasons, storing a large amount of hydrogen reversibly in a small and lightweight container safely has been the biggest challenge in realizing a hydrogen-based economy1,2,3,4,5.
Over the years, the United States Department of Energy (USDOE) has monitored the research progress in the development of hydrogen storage materials for consumer vehicles. In 2015, the USDOE set the ultimate target of 7.5 wt% for the gravimetric storage capacities of onboard hydrogen storage materials for light-duty vehicles5. As of now, there have been several methods for the storage of hydrogen1,2,3,4. The conventional methods for storing hydrogen are the high pressure method and the cryogenic method. In the high pressure method, one adopts carbon fiber reinforced tanks, which can withstand very high pressures (e.g., 350 to 700 bar), to store a large amount of completely recoverable hydrogen. In the cryogenic method, hydrogen is stored at very low temperatures (e.g., 20 K), typically requiring an expensive liquid helium refrigeration system. Both of these methods are not suitable for onboard automobile applications, because of the associated risk, high cost, and heavy weight. The storage of hydrogen in a metal hydride seems to be a convincing solution, but the irreversibility, slow kinetics, and high desorption temperature associated with this method are the problems yet to be overcome. Another promising solution is the storage of hydrogen in high surface area materials (e.g., graphene, carbon nanotubes, and metal-organic frameworks) through the adsorption-based methods. As high surface area materials could adsorb large amounts of hydrogen, the corresponding H2 gravimetric storage capacities could be rather high. Nevertheless, these materials bind H2 molecules very weakly (i.e., mainly governed by van der Waals (vdW) interactions), and hence, they perform properly only at very low temperatures.
For reversible hydrogen adsorption and desorption at ambient conditions (298 K and 1 bar), in addition to other thermodynamic considerations, the ideal binding energies of H2 molecules on hydrogen storage materials should be in the range of about 20 to 40 kJ/mol per H2 6,7,8. Consequently, various novel methods are being explored to increase the binding energies of H2 molecules on high surface area materials to the aforementioned ideal range for ambient storage applications. To increase the H2 adsorption binding energy, the surface of the adsorbent is generally modified with substitution doping, adatom adsorption, functionalization, etc.2. Among them, Li adsorption is especially attractive, because of its light weight with which a high gravimetric storage capacity could be easily achieved. Note also that Li-adsorbed carbon materials have been shown to possess relatively high gravimetric storage capacities with enhanced H2 adsorption binding energies9,10,11,12,13,14,15,16,17, through a charge-transfer induced polarization mechanism2, 18,19,20.
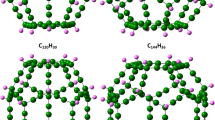
Among carbon materials, linear carbon chains (C n ), consisting of n carbon atoms bonded with sp1 hybridization (see Fig. 1(a), have recently attracted much attention owing to their unique electronic properties21,22,23,24,25,26,27,28,29,30,31,32,33,34,35. Note that C n may be considered for hydrogen storage applications due to their one-dimensional (1D) structures and the feasibility of synthesis of C n and their derivatives24,25,26,27,28,29,30. Recently, Pt-terminated linear carbon chains have been synthesized28. As mentioned above, due to a charge-transfer induced polarization mechanism2, 18,19,20, Li-terminated linear carbon chains (Li2C n ) can be good candidates for hydrogen storage materials (see Fig. 1(b–h). Because of the light elements (i.e., C and Li atoms) in Li2C n , high gravimetric storage capacities could be easily achieved. However, to the best of our knowledge, there has been no comprehensive study on the electronic and hydrogen storage properties of Li2C n in the literature, possibly due to the presence of strong static correlation effects in Li2C n (commonly occurring in 1D structures due to quantum confinement effects)36. Theoretically, the popular Kohn-Sham density functional theory (KS-DFT)37 with conventional semilocal38, hybrid39,40,41,42, and double-hybrid43,44,45,46 exchange-correlation (XC) density functionals can provide unreliable results for systems with strong static correlation effects47. For the accurate prediction of the properties of these systems, high-level ab initio multi-reference methods are typically needed48. Nonetheless, accurate multi-reference calculations are prohibitively expensive for large systems (especially for geometry optimization).
Structures of (a) C5, (b) Li2C5, (c) Li2C5 with one H2 molecule adsorbed on each Li atom, (d) Li2C5 with two H2 molecules adsorbed on each Li atom, (e) Li2C5 with three H2 molecules adsorbed on each Li atom, (f) Li2C5 with four H2 molecules adsorbed on each Li atom, (g) Li2C5 with five H2 molecules adsorbed on each Li atom, and (h) Li2C5 with six H2 molecules adsorbed on each Li atom. Here, grey, white, and purple balls represent C, H, and Li atoms, respectively.
To circumvent the formidable computational expense of high-level ab initio multi-reference methods, we have newly developed thermally-assisted-occupation density functional theory (TAO-DFT)49,50,51 for the study of large ground-state systems (e.g., containing up to a few thousand electrons) with strong static correlation effects. In contrast to KS-DFT, TAO-DFT is a density functional theory with fractional orbital occupations, wherein strong static correlation is explicitly described by the entropy contribution (see Eq. (26) of ref. 49), a function of the fictitious temperature and orbital occupation numbers. Note that the entropy contribution is completely missing in KS-DFT. Interestingly, TAO-DFT is as efficient as KS-DFT for single-point energy and analytical nuclear gradient calculations, and is reduced to KS-DFT in the absence of strong static correlation effects. Therefore, TAO-DFT can treat both single- and multi-reference systems in a more balanced way than KS-DFT. Besides, existing XC density functionals in KS-DFT may also be adopted in TAO-DFT. Due to its computational efficiency and reasonable accuracy for large systems with strong static correlation, TAO-DFT has been successfully applied to the study of several strongly correlated electron systems at the nanoscale17, 52,53,54, which are typically regarded as “challenging systems” for traditional electronic structure methods (e.g., KS-DFT with conventional XC density functionals and single-reference ab initio methods)47. Accordingly, TAO-DFT can be an ideal theoretical method for studying the electronic properties of Li2C n . Besides, the orbital occupation numbers in TAO-DFT can be useful for examining the possible radical character of Li2C n . For the hydrogen storage properties, as the interaction between H2 and Li2C n may involve dispersion (vdW) interactions, electrostatic interactions, and orbital interactions3, 7, 55, the inclusion of dispersion corrections56, 57 in TAO-DFT is important for properly describing noncovalent interactions. Therefore, in this work, we adopt TAO-DFT with dispersion corrections50 to study the electronic and hydrogen storage properties of Li2C n with various chain lengths (n = 5–10). In addition, the electronic properties of Li2C n are also compared with those of C n to examine the role of Li termination.
Computational Details
All calculations are performed with a development version of Q-Chem 4.458, using the 6–31G(d) basis set with the fine grid EML(75,302), consisting of 75 Euler-Maclaurin radial grid points and 302 Lebedev angular grid points. Results are computed using TAO-BLYP-D50 (i.e., TAO-DFT with the dispersion-corrected BLYP-D XC density functional56 and the LDA θ-dependent density functional \({E}_{\theta }^{{\rm{LDA}}}\) (see Eq. (41) of ref. 49) with the fictitious temperature θ = 7 mhartree (as defined in ref. 49).
Results and Discussion
Electronic Properties
To obtain the ground state of C n /Li2C n (n = 5–10), spin-unrestricted TAO-BLYP-D calculations are performed for the lowest singlet and triplet energies of C n /Li2C n on the respective geometries that were fully optimized at the same level of theory. The singlet-triplet energy (ST) gap of C n /Li2C n is calculated as (E T − E S), the energy difference between the lowest triplet (T) and singlet (S) states of C n /Li2C n . As shown in Fig. 2(a), the ground states of C n and Li2C n are singlets for all the chain lengths investigated.
Because of the symmetry constraint, the spin-restricted and spin-unrestricted energies for the lowest singlet state of C n /Li2C n should be the same for the exact theory49,50,51, 59. To assess the possible symmetry-breaking effects, we also perform spin-restricted TAO-BLYP-D calculations for the lowest singlet energies on the corresponding optimized geometries. The spin-restricted and spin-unrestricted TAO-BLYP-D energies for the lowest singlet state of C n /Li2C n are found to be essentially the same (within the numerical accuracy of our calculations), implying that essentially no unphysical symmetry-breaking effects occur in our spin-unrestricted TAO-BLYP-D calculations.
To assess the energetic stability of terminating Li atoms, the Li binding energy, E b (Li), on C n is computed using
where \({E}_{{{\rm{C}}}_{n}}\) is the total energy of C n , E Li is the total energy of Li, and \({E}_{{{\rm{Li}}}_{2}{{\rm{C}}}_{n}}\) is the total energy of Li2C n . E b (Li) is subsequently corrected for the basis set superposition error (BSSE) using the counterpoise correction60, where the C n is considered as one fragment, and the 2 Li atoms are considered as the other fragment. As shown in Fig. 2(b), C n can strongly bind the Li atoms with the binding energy range of 258 to 357 kJ/mol per Li.
At the ground-state (i.e., the lowest singlet state) geometry of C n /Li2C n (with N electrons), the vertical ionization potential (IP v = E N−1 − E N ), vertical electron affinity (EA v = E N − E N+1), and fundamental gap (E g = IP v − EA v = E N+1 + E N−1 − 2E N ) are obtained with multiple energy-difference calculations, with E N being the total energy of the N-electron system. For each n, Li2C n possesses the smaller IP v (see Fig. 3(a), EA v (see Fig. 3(b), and E g (see Fig. 4) values than C n . Note also that the IP v , EA v , and E g values of Li2C n are less sensitive to the chain length than those of C n .
To examine the possible radical character of C n /Li2C n , we calculate the symmetrized von Neumann entropy (e.g., see Eq. (9) of ref. 59)
for the lowest singlet state of C n /Li2C n as a function of the chain length, using TAO-BLYP-D. Here, f i the occupation number of the i th orbital obtained with TAO-BLYP-D, which varies from 0 to 1, is approximately equal to the occupation number of the i th natural orbital49,50,51, 61. For a system without strong static correlation ({f i } are close to either 0 or 1), S vN provides insignificant contributions, while for a system with strong static correlation ({f i } are fractional for active orbitals, and are close to either 0 or 1 for others), S vN increases with the number of active orbitals. As shown in Fig. 5, the S vN values of C n with even-number carbon atoms and Li2C n with odd-number carbon atoms are much larger than the S vN values of C n with odd-number carbon atoms and Li2C n with even-number carbon atoms, respectively.
To illustrate the causes of the odd-even oscillations in S vN, we plot the occupation numbers of the active orbitals for the lowest singlet states of C n (see Fig. 6(a) and Li2C n (see Fig. 6(b), calculated using TAO-BLYP-D. Here, the highest occupied molecular orbital (HOMO) is the (N/2)th orbital, and the lowest unoccupied molecular orbital (LUMO) is the (N/2 + 1)th orbital, with N being the number of electrons in C n /Li2C n . For brevity, HOMO, HOMO − 1, HOMO − 2, and HOMO − 3, are denoted as H, H − 1, H − 2, and H − 3, respectively, while LUMO, LUMO + 1, LUMO + 2, and LUMO + 3, are denoted as L, L + 1, L + 2, and L + 3, respectively. As shown, C n with even-number carbon atoms and Li2C n with odd-number carbon atoms possess more pronounced diradical character than C n with odd-number carbon atoms and Li2C n with even-number carbon atoms, respectively.
On the basis of several measures (e.g., the smaller ST gap, smaller E g , larger S vN, and more pronounced diradical character), C n with even-number carbon atoms and Li2C n with odd-number carbon atoms should exhibit much stronger static correlation effects than C n with odd-number carbon atoms and Li2C n with even-number carbon atoms (i.e., possessing single-reference character), respectively. Note that KS-DFT with conventional XC density functionals can be unreliable for the properties of systems with strong static correlation effects, and accurate multi-reference calculations are prohibitively expensive for large systems (e.g., the longer C n and Li2C n ). In addition, due to the alteration of the reactivity of C n and Li2C n with n, it is highly desirable to adopt an electronic structure method that can provide a balanced performance for both single- and multi-reference systems, well justifying the use of TAO-DFT in this study.
Hydrogen Storage Properties
As pure carbon materials bind H2 molecules very weakly (i.e., mainly governed by vdW interactions), they are unlikely to be promising hydrogen storage materials at ambient conditions6. Similarly, C n are not ideal for ambient storage applications, since the binding energies of H2 molecules remain small. In addition, the number of H2 molecules that can be adsorbed on C n is quite limited, due to the repulsive interaction between the adsorbed H2 molecules at short distances62. Consequently, the more the adsorbed H2 molecules, the less the average H2 binding energy on C n . Therefore, C n cannot be high-capacity hydrogen storage materials at ambient conditions.
Here, we investigate the hydrogen storage properties of Li2C n (n = 5–10). As illustrated in Fig. 1(b–h), at the ground-state geometry of Li2C n , x H2 molecules (x = 1–6) are initially placed on various possible sites around each Li atom, and the structures are subsequently optimized to obtain the most stable geometry. All the H2 molecules are found to be adsorbed molecularly to the Li atoms. The average H2 binding energy, E b (H2), on Li2C n is evaluated by
where \({E}_{{{\rm{H}}}_{2}}\) is the total energy of H2, and \({E}_{{{\rm{Li}}}_{2}{{\rm{C}}}_{n}-2x{{\rm{H}}}_{2}}\) is the total energy of Li2C n with x H2 molecules adsorbed on each Li atom. Subsequently, E b (H2) is corrected for BSSE using a standard counterpoise correction60. As shown in Fig. 7(a), E b (H2) is in the range of 19 to 27 kJ/mol per H2 for x = 1–4, in the range of 18 to 19 kJ/mol per H2 for x = 5, and about 16 kJ/mol per H2 for x = 6, falling in (or close to) the ideal binding energy range.
To assess if the binding energies of successive H2 molecules are also in (or close to) the ideal binding energy range (i.e., not just the average H2 binding energy), the binding energy of the y th H2 molecule (y = 1–6), E b,y (H2), on Li2C n is evaluated by
Similarly, E b,y (H2) is also corrected for BSSE using a standard counterpoise correction60. As shown in Fig. 7(b), E b,y (H2) is in the range of 16 to 27 kJ/mol per H2 for y = 1–4, in the range of 11 to 12 kJ/mol per H2 for y = 5, and less than 5 kJ/mol per H2 for y = 6. Therefore, while the first four H2 molecules can be adsorbed on Li2C n in (or close to) the ideal binding energy range, the fifth and sixth H2 molecules are only weakly adsorbed (i.e., appropriate only for storage at very low temperatures).
To assess the types of noncovalent interactions between H2 and Li2C n , we compute the atomic charge on each Li atom for Li2C n (n = 5–10) with x H2 molecules (x = 0–6) adsorbed on each Li atom (see Fig. 8), using the CHELPG (CHarges from ELectrostatic Potentials using a Grid based method) scheme63, in which atomic charges are fitted to reproduce the molecular electrostatic potential at a number of points around the molecule. For further clarification, we also plot the charge density isosurfaces of C5 and Li2C5 with x H2 molecules (x = 0–6) adsorbed on each Li atom (see Fig. 9). Similar charge density isosurfaces are also found for the longer Li2C n (n = 6–10) with the same number of adsorbed H2 molecules. As the electronegativity of C is much higher than that of Li, the transfer of electronic charge in Li2C n is from Li to C n , resulting in a positive charge of 0.67–0.79 |e| on each Li atom in Li2C n . The positively charged Li atom can interact with more than one H2 molecule, but the positive charge on Li decreases for the subsequent adsorption of H2 molecules (up to x = 3). This type of adsorption can be attributed to the polarization of H2 molecules by the positively charged Li atom (i.e., charge-induced dipole interaction)2, 18,19,20, leading to the enhanced H2 binding energy and high hydrogen uptake in Li2C n . When the number of adsorbed H2 molecules is large (e.g., x = 4–6), there is a significant overlap of the Li and H2 charge densities, enhancing orbital interactions3, 7, 55. This suggests that orbital interactions should also be responsible for the H2 binding energy, especially when a large number of H2 molecules (e.g., x = 4–6) are adsorbed on the Li atom. In particular, due to the enhanced orbital interactions, when the fourth H2 molecule is adsorbed on the Li atom, a small fraction of electronic charge is transferred from the Li atom to the adsorbed H2 molecules, slightly increasing the positive charge on Li. Interestingly, there is no overlap between the charge density of the sixth H2 molecule and the charge densities of other molecules, supporting that the sixth H2 molecule is only weakly adsorbed (i.e., mainly governed by vdW interactions). Accordingly, the noncovalent interactions between H2 and Li2C n should involve charge-induced dipole interactions, orbital interactions, and vdW interactions.
The desorption temperature, T D , of the adsorbed H2 molecules is estimated using the van’t Hoff equation13, 17, 64, 65,
where E b (H2) is the average H2 binding energy (given by Eq. (3)), ΔS is the change in hydrogen entropy from gas to liquid phase (ΔS = 13.819R taken from ref. 66), p 0 is the standard atmospheric pressure (1 bar), p eq is the equilibrium pressure, k B is the Boltzmann constant, and R is the gas constant. As shown in Table 1, T D for Li2C n (n = 5–10) with x H2 molecules (x = 1–4) adsorbed on each Li atom, is estimated using Eq. (5) at p eq = 1.5 bar (as adopted in ref. 6) and at p eq = 1 bar (the standard atmospheric pressure). As the E b (H2) values are in the range of 19.47 to 26.53 kJ/mol per H2 for x = 1–4, the corresponding T D values are in the range of 165 to 224 K at p eq = 1.5 bar, and in the range of 169 to 231 K at p eq = 1 bar, well above the easily achieved temperature of liquid nitrogen (i.e., 77 K). Therefore, Li2C n (n = 5–10) can be viable hydrogen storage materials that can uptake and release hydrogen at temperatures well above 77 K. Note that strictly, ΔS should be the change of total entropy before and after the hydrogenation. Therefore, the T D values given in Table 1 have to be taken as rough estimates for the desorption temperatures due to the definition of ΔS. For all metal-hydrogen systems, ΔS can be roughly estimated as the entropy change from molecular hydrogen gas to dissolved solid hydrogen1, that is 15.720R (taken from ref. 66), as it arises mainly from the entropy loss of gaseous hydrogen during hydrogen uptake by the metal. Since Li2C n (n = 5–10) adsorb hydrogen as a form of molecule, ΔS should be smaller than 15.720R (as the entropy of adsorbed hydrogen should be positive yet nonvanishingly small). While there is no accurate estimate of the entropy of hydrogen in adsorbed state, it should be safe to assume that it is much less than that of the gas state67. Therefore, we estimate ΔS as the entropy change from molecular hydrogen gas to liquid hydrogen, as suggested by previous studies13, 17, 64, 65. On the basis of Eq. (5), the larger the ΔS, the lower the T D values. However, even if the maximal ΔS (i.e., 15.720R) is adopted, the corresponding T D values will be only slightly lower (i.e., within 28 K for each case) than our reported T D values given in Table 1, being also well above 77 K. Accordingly, our comments remain the same even for the extreme case.
As Li2C n (n = 5–10) can bind up to 8 H2 molecules (i.e., each Li atom can bind up to 4 H2 molecules) with the average and successive H2 binding energies in (or close to) the ideal binding energy range, the corresponding H2 gravimetric storage capacity, C g , is calculated using
Here, \({M}_{{{\rm{Li}}}_{2}{{\rm{C}}}_{n}}\) is the mass of Li2C n , and \({M}_{{{\rm{H}}}_{2}}\) is the mass of H2. Note that C g (see Eq. (6)) is 17.9 wt% for n = 5, 15.8 wt% for n = 6, 14.1 wt% for n = 7, 12.8 wt% for n = 8, 11.7 wt% for n = 9, and 10.7 wt% for n = 10, satisfying the USDOE ultimate target of 7.5 wt%. Based on the observed trends for Li2C n , the maximum number of H2 molecules that can be adsorbed on each Li atom with the average and successive H2 binding energies in (or close to) the ideal binding energy range should be 4, regardless of the chain length. Therefore, the C g value of Li2C n should decrease as the chain length increases. Note, however, that the C g values obtained here may not be directly compared to the USDOE target value, which refers to the complete storage system (i.e., with the storage material, enclosing tank, insulation, piping, etc.)5. Nevertheless, since the C g values obtained here are much higher (especially for the shorter Li2C n ) than the USDOE ultimate target, the complete storage systems based on Li2C n are likely to be high-capacity hydrogen storage materials that can uptake and release hydrogen at temperatures well above the temperature of liquid nitrogen.
Conclusions
In conclusion, the search for ideal hydrogen storage materials has been extended to large systems with strong static correlation effects (i.e., those beyond the reach of traditional electronic structure methods), due to recent advances in TAO-DFT. In this work, we have studied the electronic properties (i.e., the Li binding energies, ST gaps, vertical ionization potentials, vertical electron affinities, fundamental gaps, symmetrized von Neumann entropy, and active orbital occupation numbers) and hydrogen storage properties (i.e., the average H2 binding energies, successive H2 binding energies, H2 desorption temperatures, and H2 gravimetric storage capacities) of Li2C n (n = 5–10) using TAO-DFT. As Li2C n with odd-number carbon atoms have been shown to possess pronounced diradical character, KS-DFT with conventional XC density functionals can be unreliable for studying the properties of these systems. In addition, accurate multi-reference calculations are prohibitively expensive for the longer Li2C n (especially for geometry optimization), and hence, the use of TAO-DFT in this study is well justified. On the basis of our results, Li2C n can bind up to 8 H2 molecules (i.e., each Li atom can bind up to 4 H2 molecules) with the average and successive H2 binding energies in (or close to) the ideal range of about 20 to 40 kJ/mol per H2. Accordingly, the H2 gravimetric storage capacities of Li2C n are in the range of 10.7 to 17.9 wt%, satisfying the USDOE ultimate target of 7.5 wt%. Consequently, Li2C n can be high-capacity hydrogen storage materials that can uptake and release hydrogen at temperatures well above the easily achieved temperature of liquid nitrogen.
For the practical realization of hydrogen storage based on Li2C n , Li2C n may be adopted as building blocks. For example, we may follow the proposal of Liu et al.68, and consider connecting Li-coated fullerenes with Li2C n , which could also serve as high-capacity hydrogen storage materials. A systematic study of the electronic and hydrogen storage properties of these systems is essential, and may be considered for future work. Since linear carbon chains26, 27 and Pt-terminated linear carbon chains28 have been successfully synthesized, the realization of hydrogen storage materials based on Li2C n should be feasible, and is now open to experimentalists. In the future, we plan to examine how the electronic and hydrogen storage properties of linear carbon chains vary with different metal dopants (e.g., Na, Al, Ca, Ti, etc.).
References
Schlapbach, L. & Züttel, A. Hydrogen-storage materials for mobile applications. Nature 414, 353–358 (2001).
Jena, P. Materials for hydrogen storage: past, present, and future. J. Phys. Chem. Lett. 2, 206–211 (2011).
Park, N. et al. Progress on first-principles-based materials design for hydrogen storage. PNAS 109, 19893–19899 (2012).
Dalebrook, A. F., Gan, W., Grasemann, M., Moret, S. & Laurenczy, G. Hydrogen storage: beyond conventional methods. Chem. Commun. 49, 8735–8751 (2013).
U. S. Department of Energy, Target explanation document: onboard hydrogen storage for light-duty fuel cell vehicles. Technical report. Available at: https://energy.gov/eere/fuelcells/hydrogen-storage (Accessed: January 2017) (2015).
Bhatia, S. K. & Myers, A. L. Optimum conditions for adsorptive storage. Langmuir 22, 1688–1700 (2006).
Lochan, R. C. & Head-Gordon, M. Computational studies of molecular hydrogen binding affinities: the role of dispersion forces, electrostatics, and orbital interactions. Phys. Chem. Chem. Phys. 8, 1357–1370 (2006).
Sumida, K. et al. Impact of metal and anion substitutions on the hydrogen storage properties of M-BTT metal-organic frameworks. J. Am. Chem. Soc. 135, 1083–1091 (2013).
Chen, P., Wu, X., Lin, J. & Tan, K. L. High H2 uptake by alkali-doped carbon nanotubes under ambient pressure and moderate temperatures. Science 285, 91–93 (1999).
Deng, W.-Q., Xu, X. & Goddard, W. A. New alkali doped pillared carbon materials designed to achieve practical reversible hydrogen storage for transportation. Phys. Rev. Lett. 92, 166103 (2004).
Li, A. et al. Lithium-doped conjugated microporous polymers for reversible hydrogen storage. Angew. Chemie Int. Ed. 49, 3330–3333 (2010).
Seenithurai, S., Kodi Pandyan, R., Vinodh Kumar, S., Saranya, C. & Mahendran, M. Li-decorated double vacancy graphene for hydrogen storage application: a first principles study. Int. J. Hydrogen Energy 39, 11016–11026 (2014).
Qiu, N.-X., Zhang, C.-H. & Xue, Y. Tuning hydrogen storage in lithium-functionalized BC2N sheets by doping with boron and carbon. Chem Phys Chem 15, 3015–3025 (2014).
Hussain, T., De Sarkar, A. & Ahuja, R. Functionalization of hydrogenated graphene by polylithiated species for efficient hydrogen storage. Int. J. Hydrogen Energy 39, 2560–2566 (2014).
Hussain, T. et al. Hydrogen storage properties of light metal adatoms (Li, Na) decorated fluorographene monolayer. Nanotechnology 26, 275401 (2015).
Hussain, T., Hankel, M. & Searles, D. J. Computational evaluation of lithium-functionalized carbon nitride (g-C6N8) monolayer as an efficient hydrogen storage material. J. Phys. Chem. C 120, 25180–25188 (2016).
Seenithurai, S. & Chai, J.-D. Effect of Li adsorption on the electronic and hydrogen storage properties of acenes: a dispersion-corrected TAO-DFT study. Sci. Rep. 6, 33081 (2016).
Niu, J., Rao, B. K. & Jena, P. Binding of hydrogen molecules by a transition-metal ion. Phys. Rev. Lett. 68, 2277–2280 (1992).
Niu, J., Rao, B. K., Jena, P. & Manninen, M. Interaction of H2 and He with metal atoms, clusters, and ions. Phys. Rev. B 51, 4475–4484 (1995).
Froudakis, G. E. Why alkali-metal-doped carbon nanotubes possess high hydrogen uptake. Nano Lett. 1, 531–533 (2001).
Fan, Q. & Pfeiffer, G. V. Theoretical study of linear C n (n = 6–10) and HC n H (n = 2–10) molecules. Chem. Phys. Lett. 162, 472–478 (1989).
Heimann, R. B. In Carbyne and Carbynoid Structures (eds Heimann, R. B. et al.) (Kluwer Academic Publishers, 1999).
Horný, L., Petraco, N. D. K. & Schaefer, H. F. III Odd carbon long linear chains HC2n+1H (n = 4–11): Properties of the neutrals and radical anions. J. Am. Chem. Soc. 124, 14716–14720 (2002).
Van Zee, R. J., Ferrante, R. F., Zeringue, K. J., Weltner, W. Jr. & Ewing, D. W. Electron spin resonance of the C6, C8, and C10 molecules. J. Chem. Phys. 88, 3465 (1988).
Pan, L., Rao, B. K., Gupta, A. K., Das, G. P. & Ayyub, P. H-substituted anionic carbon clusters C n H− (n ≤ 10): Density functional studies and experimental observations. J. Chem. Phys. 119, 7705 (2003).
Jin, C., Lan, H., Peng, L., Suenaga, K. & Iijima, S. Deriving carbon atomic chains from graphene. Phys. Rev. Lett. 102, 205501 (2009).
Chuvilin, A., Meyer, J. C., Algara-Siller, G. & Kaiser, U. From graphene constrictions to single carbon chains. New J. Phys. 11, 083019 (2009).
Kano, E., Takeguchi, M., Fujita, J.-I. & Hashimoto, A. Direct observation of Pt-terminating carbyne on graphene. Carbon 80, 382–386 (2014).
Banhart, F. Chains of carbon atoms: a vision or a new nanomaterial? Beilstein J. Nanotechnol. 6, 559–569 (2015).
Casari, C. S., Tommasini, M., Tykwinski, R. R. & Milani, A. Carbon-atom wires: 1-D systems with tunable properties. Nanoscale 8, 4414–4435 (2016).
Belau, L. et al. Ionization thresholds of small carbon clusters: tunable VUV experiments and theory. J. Am. Chem. Soc. 129, 10229–10243 (2007).
Lang, N. D. & Avouris, P. Oscillatory conductance of carbon-atom wires. Phys. Rev. Lett. 81, 3515 (1998).
Souza, A. M. C. & Herrmann, H. Theory of local electronic properties and finite-size effects in nanoscale open chains. Phys. Rev. B 77, 085416 (2008).
Li, Z. Y. et al. Magnetism and spin-polarized transport in carbon atomic wires. Phys. Rev. B 80, 115429 (2009).
Artyukhov, V. I., Liu, M. & Yakobson, B. I. Mechanically induced metal-insulator transition in carbyne. Nano Lett. 14, 4224–4229 (2014).
Brus, L. Size, dimensionality, and strong electron correlation in nanoscience. Acc. Chem. Res. 47, 2951–2959 (2014).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Lin, Y.-S., Tsai, C.-W., Li, G.-D. & Chai, J.-D. Long-range corrected hybrid meta-generalized-gradient approximations with dispersion corrections. J. Chem. Phys. 136, 154109 (2012).
Lin, Y.-S., Li, G.-D., Mao, S.-P. & Chai, J.-D. Long-range corrected hybrid density functionals with improved dispersion corrections. J. Chem. Theory Comput. 9, 263–272 (2013).
Wang, C.-W., Hui, K. & Chai, J.-D. Short- and long-range corrected hybrid density functionals with the D3 dispersion corrections. J. Chem. Phys. 145, 204101 (2016).
Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 124, 034108 (2006).
Chai, J.-D. & Head-Gordon, M. Long-range corrected double-hybrid density functionals. J. Chem. Phys. 131, 174105 (2009).
Chai, J.-D. & Mao, S.-P. Seeking for reliable double-hybrid density functionals without fitting parameters: the PBE0-2 functional. Chem. Phys. Lett. 538, 121–125 (2012).
Hui, K. & Chai, J.-D. SCAN-based hybrid and double-hybrid density functionals from models without fitted parameters. J. Chem. Phys. 144, 044114 (2016).
Cohen, A. J., Mori-Sánchez, P. & Yang, W. Challenges for density functional theory. Chem. Rev. 112, 289–320 (2012).
Gryn’ova, G., Coote, M. L. & Corminboeuf, C. Theory and practice of uncommon molecular electronic configurations. WIREs Comput. Mol. Sci. 5, 440–459 (2015).
Chai, J.-D. Density functional theory with fractional orbital occupations. J. Chem. Phys. 136, 154104 (2012).
Chai, J.-D. Thermally-assisted-occupation density functional theory with generalized-gradient approximations. J. Chem. Phys. 140, 18A521 (2014).
Chai, J.-D. Role of exact exchange in thermally-assisted-occupation density functional theory: a proposal of new hybrid schemes. J. Chem. Phys. 146, 044102 (2017).
Wu, C.-S. & Chai, J.-D. Electronic properties of zigzag graphene nanoribbons studied by TAO-DFT. J. Chem. Theory Comput. 11, 2003–2011 (2015).
Yeh, C.-N. & Chai, J.-D. Role of Kekulé and non-Kekulé structures in the radical character of alternant polycyclic aromatic hydrocarbons: a TAO-DFT study. Sci. Rep 6, 30562 (2016).
Wu, C.-S., Lee, P.-Y. & Chai, J.-D. Electronic properties of cyclacenes from TAO-DFT. Sci. Rep. 6, 37249 (2016).
Tsivion, E., Long, J. R. & Head-Gordon, M. Hydrogen physisorption on metal-organic framework linkers and metalated linkers: a computational study of the factors that control binding strength. J. Am. Chem. Soc. 136, 17827–17835 (2014).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Grimme, S., Hansen, A., Brandenburg, J. G. & Bannwarth, C. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 116, 5105–5154 (2016).
Shao, Y. et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 113, 184–215 (2015).
Rivero, P., Jiménez-Hoyos, C. A. & Scuseria, G. E. Entanglement and polyradical character of polycyclic aromatic hydrocarbons predicted by projected Hartree-Fock theory. J. Phys. Chem. B 117, 12750–12758 (2013).
Boys, S. F. & Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 19, 553–566 (1970).
Löwdin, P.-O. & Shull, H. Natural orbitals in the quantum theory of two-electron systems. Phys. Rev. 101, 1730–1739 (1956).
Okamoto, Y. & Miyamoto, Y. Ab initio investigation of physisorption of molecular hydrogen on planar and curved graphenes. J. Phys. Chem. B 105, 3470–3474 (2001).
Breneman, C. M. & Wiberg, K. B. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 11, 361–373 (1990).
Durgun, E., Ciraci, S. & Yildirim, T. Functionalization of carbon-based nanostructures with light transition-metal atoms for hydrogen storage. Phys. Rev. B 77, 085405 (2008).
Chakraborty, B., Modak, P. & Banerjee, S. Hydrogen storage in yttrium-decorated single walled carbon nanotube. J. Phys. Chem. C 116, 22502–22508 (2012).
Lemmon, E. W. In Handbook of Chemistry and Physics 96th edn (eds Haynes, W. M. et al.) Section 6, 21–37 (CRC Press, 2016).
Li, J. et al. Theoretical evaluation of hydrogen storage capacity in pure carbon nanostructures. J. Chem. Phys. 119, 2376–2385 (2003).
Liu, C.-S., An, H., Guo, L.-J., Zeng, Z. & Ju, X. Theoretical realization of cluster-assembled hydrogen storage materials based on terminated carbon atomic chains. J. Chem. Phys. 134, 024522 (2011).
Acknowledgements
This work was supported by the Ministry of Science and Technology of Taiwan (Grant No. MOST104-2628-M-002-011-MY3), National Taiwan University (Grant No. NTU-CDP-105R7818), the Center for Quantum Science and Engineering at NTU (Subproject Nos.: NTU-ERP-105R891401 and NTU-ERP-105R891403), and the National Center for Theoretical Sciences of Taiwan. S.S. would like to thank Kerwin Hui and Chih-Ying Lin for useful discussions.
Author information
Authors and Affiliations
Contributions
S.S. and J.-D.C. designed the project. S.S. performed the calculations. S.S. and J.-D.C. contributed to the data analysis and writing of the paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Seenithurai, S., Chai, JD. Effect of Li Termination on the Electronic and Hydrogen Storage Properties of Linear Carbon Chains: A TAO-DFT Study. Sci Rep 7, 4966 (2017). https://doi.org/10.1038/s41598-017-05202-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-05202-6
This article is cited by
-
A first principle study of hydrogen storage in titanium-doped small carbon clusters (C2nTin, n = 2–6)
Structural Chemistry (2021)
-
TAO-DFT investigation of electronic properties of linear and cyclic carbon chains
Scientific Reports (2020)
-
Electronic Properties of Möbius Cyclacenes Studied by Thermally-Assisted-Occupation Density Functional Theory
Scientific Reports (2019)
-
Electronic Properties of Linear and Cyclic Boron Nanoribbons from Thermally-Assisted-Occupation Density Functional Theory
Scientific Reports (2019)
-
Electronic and Hydrogen Storage Properties of Li-Terminated Linear Boron Chains Studied by TAO-DFT
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.