Abstract
Novel genomics-based approaches such as genome-wide association studies (GWAS) and genomic selection (GS) are expected to be useful in fruit tree breeding, which requires much time from the cross to the release of a cultivar because of the long generation time. In this study, a citrus parental population (111 varieties) and a breeding population (676 individuals from 35 full-sib families) were genotyped for 1,841 single nucleotide polymorphisms (SNPs) and phenotyped for 17 fruit quality traits. GWAS power and prediction accuracy were increased by combining the parental and breeding populations. A multi-kernel model considering both additive and dominance effects improved prediction accuracy for acidity and juiciness, implying that the effects of both types are important for these traits. Genomic best linear unbiased prediction (GBLUP) with linear ridge kernel regression (RR) was more robust and accurate than GBLUP with non-linear Gaussian kernel regression (GAUSS) in the tails of the phenotypic distribution. The results of this study suggest that both GWAS and GS are effective for genetic improvement of citrus fruit traits. Furthermore, the data collected from breeding populations are beneficial for increasing the detection power of GWAS and the prediction accuracy of GS.
Similar content being viewed by others
Introduction
Citrus are among the most produced fruits in the world1 and contain various functional compounds beneficial for human health such as vitamins, limonoids, and carotenoids2. Total citrus fruit production in 2012 was estimated at 131.3 million tons (20% of total fruit production; 8.8 kha), of which 52.6% were sweet oranges (Citrus sinensis (L.) Osbeck), 21.1% mandarins (C. reticulata Blanco), 11.2% lemons (C. limon (L.) Burm. f.) and limes (C. aurantifolia (Christm.) Swingle), and 6.2% grapefruit (C. paradisi Macfad.) and pummelos (C. maxima Merr.)3. Widely distributed commercial cultivars have been selected from various indigenous cultivars as somatic mutants (bud sports or nucellar seedlings)4. Although mutant selection is a simple approach to improve a trait, cross-breeding is beneficial for developing novel cultivars with unprecedented trait combinations. Swingle and Webber first initiated a systematic cross-breeding program of citrus at the U.S. Department of Agriculture in Florida, USA in 1893, and they selected some important cultivars by cross-breeding5. The available combinations of crosses and the number of individuals in the population limit the efficiency of selection. Large plant size limits the number of fruit trees in orchards, and their long juvenile period lengthens the time required for breeding, thus increasing the total cost of cross-breeding. During implementation of the citrus breeding program at the National Agriculture and Food Research Organization Institute of Fruit Tree and Tea Science (NIFTS) in Japan, various techniques to promote flowering and fruiting of the seedlings to shorten the breeding cycles and grafting and training methods were established6, 7; however, the average breeding period from the cross to the release of a cultivar is still 25 years. The number of seedlings to be grafted at the orchard is the key step limiting breeding efficiency. Therefore, selecting promising seedlings at an early stage before grafting would greatly increase the probability of obtaining promising candidates.
In recent years, next-generation sequencing technologies have decreased the cost of single nucleotide polymorphism (SNP) genotyping and expanded the availability of numerous markers8. Genome-wide association studies (GWAS) and genomic selection (GS), both performed by using genome-wide markers, are becoming important and effective tools for plant breeding9, 10. GWAS enable the detection of quantitative trait loci (QTLs) or causal genes from association between genome-wide markers and trait phenotypes, and outperform bi-parental QTL mapping because GWAS do not require the development of segregating populations11, 12. GS enables the selection of superior genotypes based on genomic estimated breeding values (GEBV) estimated from information on genome-wide markers, and is more effective than marker-assisted selection (MAS), especially for traits controlled by a large number of genes13, 14. In general, the power of GWAS and the accuracy of GS are boosted when sample size is large11, 15. However, accumulating large data sets sufficient for these analyses is difficult for fruit trees because of their long juvenile period, large plant size, and difficulties in phenotyping. Poland suggested the idea of “breeding-assisted genomics”, in which the data collected from actual breeding populations is used for functional genomics in plants16. In fruit tree breeding, phenotypic data accumulated every year in conventional breeding programs could be useful for GWAS and GS. Although a number of GWAS and GS studies have been reported in animals and plants11, 13, 14, the potential for using multiple actual breeding populations in combination with the parental population has not yet been explored.
The objective of this study was to assess the potential of GWAS and GS for the genetic improvement of citrus and to evaluate the potential of using multiple actual breeding populations in addition to the parental population for GWAS and GS.
Results
Linkage disequilibrium and population structure
The levels of linkage disequilibrium (LD) in the parental population (111 varieties; Supplementary Table S1) and combined parental and breeding populations (Supplementary Table S2; 787 genotypes in total) were evaluated by calculating the squared allele-frequency correlation (r 2) between each pair of SNPs on the same chromosome. The r 2 values were plotted against the physical distance for the parental population and the combined population; curves fitted for the relationships between r 2 and physical map distance indicated that LD extended over 1 Mb (r 2 > 0.25) and decayed to relatively low levels (r 2 < 0.10) within 20 Mb in both populations (Fig. 1). The mean LD between adjacent SNPs was similar (r 2 = 0.45) in both populations, although the decay of LD was slightly faster in the combined population. The patterns of LD decay were similar in all chromosomes (Supplementary Fig. S1).
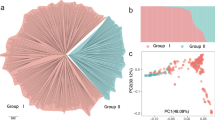
The genetic structure of the parental population was estimated by using hierarchical clustering, ADMIXTURE clustering, and principal component analysis (PCA). Hierarchical clustering divided the parental population into two major clusters (Fig. 2A). The smaller cluster contained mainly pummelos, which are large-fruit varieties (Fig. 2C; Supplementary Table S1). The larger cluster was further divided into two major sub-clusters (Fig. 2A). The smaller sub-cluster contained mainly mandarins, which are small-fruit varieties (Fig. 2C; Supplementary Table S1). According to ADMIXTURE clustering, the optimal number (K) was estimated as 4, because cross-validation (CV) error rapidly decreased until K = 4 and changed little thereafter, although K = 6 corresponded to the lowest CV error (Supplementary Fig. S2). The deduced optimal K value was similar to those reported by Curk et al.17. The cluster containing large-fruit varieties but not the sub-cluster containing small-fruit varieties showed clear genetic differentiation (Fig. 2B). Similarly, PCA indicated the presence of two main clusters, one with large and the other one with small fruit size (Supplementary Fig. S3). Whereas part of the parental population belonged to the clusters of large- or small-fruit varieties, most varieties showed no clear separation in hierarchical clustering, ADMIXTURE clustering, or PCA. PCA also suggested low stratification in the combined population (Supplementary Fig. S4).
Genetic and phenotypic population structure of the parental population. (A) Ward’s hierarchical clustering based on Euclidean distance between genotypes. (B) ADMIXTURE-based estimation of the admixture proportions of individuals. Each color represents the inferred genetic contributions from K ancestral populations. (C) Heat map of log-converted fruit weight values.
Genome-wide association study
GWAS was carried out for 17 fruit quality traits (Table 1) in the combined and parental populations (Fig. 3; Supplementary Table S3; Supplementary Figs S5 and S6). Higher –log10(p) values and/or more significant SNPs (false discovery rate <0.05) were detected for 15 traits (except for aroma intensity (Aroma) and bitterness (Bitter)) by using the combined population rather than the parental population. In the combined population, GWAS detected significant SNPs associated with 11 traits: fruit weight (Weight), fruit hardness (FruH), color of pericarp (ColorP), easiness of peeling (Peeling), color of flesh (ColorF), flesh hardness (FleH), juiciness (Juicy), firmness of locule membrane (FirmLM), number of seeds (Seed), Bitter, and acidity (Acid) (Supplementary Table S4). For the highly correlated phenotypic traits (r > 0.75; Supplementary Table S5), several common significant SNPs were detected: seven on chromosomes (Chr.) 2, 4, and 6 for ColorP and ColorF (r = 0.81) and three on Chr. 3 for FruH and Peeling (r = 0.76). Single common significant SNPs were detected for FleH and Juicy (Chr. 4; r = 0.68); FirmLM and Seed (Chr. 4; r = 0.35); and ColorP, ColorF, and Bitter (Chr. 6). A single common significant SNP for Weight, ColorP, Bitter, and Acid (Chr. 4) is consistent with the largest (although not significant) peak SNP for sugar content (Brix).
Manhattan plots for 17 fruit quality traits in the combined parental and breeding populations. Mixed linear model used four principal components of population structure as covariates (Supplementary Fig. S6). Dashed lines indicate a false discovery rate of 0.05.
Two genes, Ciclev10031587 m.g and Ciclev10031003 m.g, were found between the significant SNPs on Chr. 4 for ColorP and ColorF; these genes were located 490 kb and 17 kb apart from the nearest significant SNPs, respectively, within a high-LD region (Supplementary Fig. S7). These genes are annotated as phytoene desaturation 1 (pds1) and carotenoid cleavage dioxygenase 4 (ccd4), respectively. A significant SNP on Chr. 3 for FruH and Peeling resided in the gene Ciclev10018456 m.g, which is annotated as callose synthase. This gene was also located in the region flanking a significant SNP for FleH. The common significant SNP on Chr. 4 for Weight, ColorP, Bitter, and Acid resided in the gene Ciclev10031681 m.g, which is annotated as glutamate dehydrogenase.
Accuracy of prediction models for 17 fruit traits in the parental population
Ten-fold CV showed that prediction accuracy was high for Weight, FruH, ColorP, Peeling, ColorF, and FirmLM (r ≥ 0.7), intermediate for fruit shape (Shape), smoothness of pericarp (SmoothP), Aroma, FleH, Juicy, Seed, Bitter, taste (Taste), Brix, and Acid (0.3 ≤ r < 0.7), and low for appearance (Appear) (r < 0.3) (Fig. 4A). GBLUP (RR and GAUSS), Ridge Regression, and Bayesian regressions were more accurate for most traits than the other methods, whereas the accuracies of Random Forest, Elastic Net, and Lasso were trait-dependent. While the prediction accuracy level of a single method considerably varied among traits, the mean prediction of all 11 methods showed consistent accuracy, i.e., an upper-middle level of accuracy among the methods, for all traits. The non-linear method GBLUP (GAUSS) had the highest prediction accuracy for Acid. Because most of the traits (except Weight, Brix, and Acid) were scored as ordinal categorical traits, several prediction models specific for categorical responses were used. Because the prediction accuracy of these models was lower than that of models for continuous responses (Supplementary Fig. S8), the latter models were used for subsequent analyses.
Comparison of prediction models using the parental population. Prediction accuracy was measured as the Pearson’s correlation coefficient (r) between predicted genotypic values and phenotypic values. (A) Twelve methods were tested. RR: ridge kernel regression, GAUSS: Gaussian kernel regression. (B) Regression models were built based on the results of GWAS. The three SNPs that showed high –log10(p) values in GWAS (red points in Supplementary Fig. S5) were selected. MLR: Multiple Leaner Regression. (C) Prediction models that considered only additive or both additive and dominance effects were used.
We built prediction models that included the information from GWAS for the 17 traits. For 15 traits (except Appear and Bitter), GBLUP (RR) that treats all SNPs as random effects was more accurate than multiple linear regression (MLR) that treats the three most significant SNPs (r < 0.6; red points in Supplementary Fig. S5) as fixed effects, or GBLUP (RR) that treats the three most significant SNPs as fixed effects and other SNPs as random effects, even though MLR had high prediction accuracies (r > 0.7) for ColorP, ColorF, and FirmLM (Fig. 4B).
A multi-kernel model considering dominance and additive genetic effects was also evaluated. For Acid and Juicy, this model was more accurate than a model with only additive effects, whereas opposite results were obtained for Appear, Shape, SmoothP, FleH, Seed, and Taste (Fig. 4C). For the other traits, accuracies were similar for both models. The additive genetic effects were the major factor contributing to genetic variation for 14 traits (except Appear, Juicy, and Bitter) (Supplementary Table S6).
Prediction for distribution tails
As described above, a diversity of fruit weight was found in the parental population (Fig. 2; Supplementary Fig. S9A). Because the fruit weight of pummelos, such as ‘Egami buntan’, ‘Banpeiyu’, ‘Mato buntan’, and ‘Hirado buntan’, was very large (>800 g), we hypothesized that a genetic system differs between the varieties with extremely large fruits and other varieties. To validate the hypothesis, we tried to predict fruit weight in the large-fruit group (Fig. 2) by using a model built based on the data of other citrus varieties. The results showed a high accuracy of such prediction (Fig. 5A). Higher accuracy was attained by GBLUP (RR) (r = 0.89) than by GBLUP (GAUSS) (r = 0.74), whereas the accuracy of GBLUP (RR) was slightly lower than that of GBLUP (GAUSS) for all ranges of fruit weight (Fig. 4A). The extremely large fruit weight in pummelos was properly predicted, especially with GBLUP (RR). Similarly, GBLUP (RR) had a slightly higher accuracy for the small-fruit group (Fig. 5B). We also applied rank-ordered 4-fold CV for all 17 traits. GBLUP (RR) attained higher accuracy than did GBLUP (GAUSS) (including the number of outliers) for distribution tails for all the traits (Supplementary Fig. S9).
Prediction for fruit weight distribution tails. (A) All varieties except those in the large-fruit group (Fig. 2C), which is indicated by pink points, were used as the training set of the prediction model; the large-fruit group was used as the test set. (B) All varieties except those in the small-fruit group (Fig. 2C), which is indicated by blue points, were used as the training set; the small-fruit group was used as the test set. Grey points indicate the results of leave-one-out cross-validation. Predicted and observed values indicate log-transformed Weight. Pearson’s correlation coefficient (r) between predicted and observed values for the pink or blue points are shown on the plots. RR: linear ridge kernel regression, GAUSS: non-linear Gaussian kernel regression.
Prediction for the breeding population
To evaluate the prediction accuracy in the breeding population, three different training populations for modeling were compared. For 13 traits (except Shape, ColorP, Bitter, and Taste; Fig. 6, Supplementary Fig. S10), the accuracy of the model based on the breeding population was on average 1.35 times that of the model based on the parental population, indicating that information from the breeding population improved prediction accuracy. The highest accuracy was attained in the model based on the combined population for 14 traits (except Aroma, Bitter, and Taste). The results were similar when prediction accuracy was evaluated on a single-family basis (Supplementary Fig. S11).
Prediction accuracy of the breeding population. Prediction accuracy was measured as the Pearson’s correlation coefficient (r) between predicted genotypic values and phenotypic values. The prediction accuracy was calculated for combined all families. Only the mean prediction accuracy of all the methods is shown (Supplementary Fig. S10). Training populations are shown in the figure key. When the breeding population or combined parental and breeding populations were used as training sets, one family was excluded and its phenotype was predicted.
Discussion
The LD pattern is a key factor influencing the power of GWAS and the accuracy of GS, because these two approaches are based on LD between markers and causal polymorphisms9, 11, 13, 18. Generally, the range of LD is smaller in heterozygous outcrossing species than in homozygous selfing species19, 20, and therefore a large number of markers are needed to cover the genome of outcrossing species. In the citrus population used in this study, we observed a wide range of LD (r 2 > 0.25 at 1 Mb; Fig. 1), even though most genotypes obtained from conventional cross-breeding are highly heterozygous21. Because the citrus population has experienced a population bottleneck, i.e. it had a limited number of founders3, the wide range of LD19, 20 was expected to increase. Citrus cultivars are developed through a small number of generations, and are mainly maintained through vegetative propagation. These breeding and management systems make recombination unlikely to occur and may also maintain LD22. The mean r 2 between adjacent markers has been used to determine target marker densities for GS. For high-heritability traits, a mean r 2 of 0.15 is sufficient, but for low-heritability traits increasing the r 2 to 0.2 improved prediction accuracy23. In the citrus population used in this study, mean r 2 (0.45) was higher than the above value, suggesting that marker densities in the population would be sufficient for GS.
Population structure extends the range of LD24 and can cause spurious associations in GWAS11. Hierarchical clustering, ADMIXTURE clustering, and PCA showed that some varieties in the parental population formed clusters related to fruit weight, but most varieties showed no clear separation. The wide range of LD observed in the parental population was probably due to its small size rather than to the population structure. Given the wide range and high level of LD and the weak population structure, GWAS and GS would be effective in citrus populations.
For most traits, the number of significant SNPs and the –log10(p) values of peaks detected in GWAS were greater with the combined (787 genotypes in total) than with the parental population (111 varieties), which would increase the chance of finding good markers for MAS. These results indicate that GWAS using the combined population has higher statistical power for detecting QTLs than GWAS using only the parental population, and that the QTLs detected were shared between the parental and breeding populations. For some traits, the significant SNPs differ between the combined and parental populations, possibly because of the differences between the populations in detection power, allele frequency, or population structure.
In addition to the sample size, the difference in the LD pattern between the combined and parental populations can influence the resolution of GWAS. For example, multi-breed GWAS had a higher resolution than within-breed GWAS in dairy cattle25. This difference was explained by narrower QTL regions because of the short conserved regions of LD across breeds26. In the present study, the LD decay was rapid in the combined population, although the mean LD between adjacent SNPs was similar (r 2 = 0.45) in both populations, implying that the LD in the combined population is conserved over shorter distances than that in the parental population. The short conserved regions of LD could improve the precision of QTL detection in the combined population by narrowing down the QTL regions.
GWAS in the combined population detected SNPs significantly associated (false discovery rate <0.05) with 11 traits. The most significant association was detected for Weight on Chr. 8 where one QTL named FW8 for fruit weight has been identified in a bi-parental QTL mapping study that used a mandarin F1 population derived from ‘Fortune’ × ‘Murcott’27. The most significant SNP detected for Weight resided in the same region as FW8, confirming a single major QTL for fruit weight on Chr. 8.
Identification of seven common significant SNPs for ColorP and ColorF suggests a close genetic linkage between QTLs controlling these traits, resulting in high phenotypic correlation. Common significant SNPs for other traits could be explained similarly. Significant SNPs for ColorP and ColorF on Chr. 4 were located in multiple QTLs for fruit flavedo and juice color identified on the linkage group MUR4.127. Two genes, Ciclev10031587 m.g and Ciclev10031003 m.g, annotated as pds1 and ccd4 respectively, are colocalized with the QTLs on MUR4.127. The pds1 gene is involved in the carotenoid biosynthetic pathway in citrus28, 29 and Arabidopsis30, whereas ccd4 is involved in carotenoid accumulation in peach31, 32. The pericarp and flesh color of citrus fruits is determined by carotenoid accumulation3.
A significant SNP for FruH and Peeling on Chr. 3 resides in the callose synthase gene (Ciclev10018456 m.g). The polysaccharide callose is a component of plant cell wall33. Cell wall polysaccharides are associated with cell wall elasticity and viscosity, which influence fruit firmness. Softening of fruit tissues in tomato and avocado is caused by the degradation of cell wall polysaccharides34, 35.
A single significant SNP for Acid detected on Chr. 4 is consistent with those for Weight, ColorP, and Bitter, and with the largest (although not significant) peak SNP for Brix. This SNP resides in the gene Ciclev10031681 m.g, which is annotated as glutamate dehydrogenase. In avocado, the activity and protein content of GDH remain constant during fruit development, but increase ~4-fold during fruit ripening36. Generally, the acidity decreases while the sugar content increases during fruit maturation3. GDH could have pleiotropic effects on fruit quality traits involved in citrus fruit maturation. If so, common significant SNPs could be used as common markers for such traits in MAS programs.
The prediction accuracy of GBLUP (RR) that treats all SNPs as random effects, was highest for all the traits except Appear and Bitter, implying that all the traits except Appear and Bitter are controlled by many genes and/or QTLs. For Shape, SmoothP, Aroma, Taste, and Brix, for which the levels of prediction accuracy were intermediate, even though no significant association was detected. These results suggest that GS is more accurate for these traits than MAS based on significant SNPs. On the other hand, high prediction accuracies (r > 0.7) of MLR for ColorP, ColorF, and FirmLM imply that MAS performed by using a few markers enables the selection at low-cost genotyping for these traits.
A multi-kernel model that considers both additive and dominance effects improved the accuracy for Acid and Juicy, suggesting that the effects of both types are important for these traits. The highest prediction accuracy of GBLUP (GAUSS) for Acid supports this idea. Whereas GBLUP (RR) captures additive genetic effects, GBLUP (GAUSS) captures non-additive genetic effects (e.g., the dominance effect) by modeling non-linear relationships between markers and the phenotype37, 38. For the other traits, prediction accuracy was similar or lower with the model considering additive and dominance effects, suggesting that additive models are sufficient to explain genetic variations in the population. Consistent with this assumption, additive genetic effects were the major factor contributing to genetic variation. Using models that consider both additive and dominance effects may not always be beneficial, as suggested by several previous studies. Adding dominance and epistatic effects to additive genetic effects did not help genomic prediction in rice, suggesting a high correlation between multiple variance components39. In wheat, considering only additive effects resulted in equal or even higher prediction accuracy than considering both additive and dominance effects40, even though considering both types of effects increased the prediction accuracy in another simulation study that used a large population41. These results suggest that models considering dominance effects are quite sensitive to the number of individuals in the population40.
The prediction for the tails of fruit weight distribution was accurate for large-fruit varieties. The extremely large fruit weight of pummelos was properly predicted, especially with GBLUP (RR), even though the accuracy of GBLUP (RR) for the whole range of distribution was slightly lower than that of GBLUP (GAUSS). This implies that the genetic architecture of the extremely large fruit weight of pummelos can be explained by the additive accumulation of fruit weight–related genes of “non-large-fruit” varieties, which include a number of mandarins and sweet oranges. Cultivated pummelos were originally selected from a single progenitor species, C. maxima, whilst some of the cultivated mandarins were developed by introgression from C. maxima to the ancestral mandarin species C. reticulata 42; sweet oranges (C. sinensis) originated from pummelo and mandarin43. Thus, mandarins and sweet oranges are related to pummelos, which may have contributed to the high prediction accuracy for the extremely large fruit weight of pummelos. For other traits, RR also outperformed GAUSS in the prediction of the distribution tails, suggesting that RR is much more robust and accurate than GAUSS when used for this purpose. This is an important implication for the use of GS in breeding programs, because the prediction of distribution tails is important for increasing or decreasing genotypic values of target traits.
For the breeding population, the prediction accuracy was lower in the model built using only the parental population than in the model built using the combined population. This result suggests that the high genetic diversity in the parental population is not always useful to predict a small variation in the breeding population. Generally, the prediction accuracy across populations that are of low relevance is lower than that within a population44. Lower prediction accuracies across populations than within populations were also observed in apple45, 46, grapevine47 and maize48. On the other hand, across-population evaluation is reportedly preferable to that within populations when the populations are closely related to each other, marker density is high, or the number of phenotypic records is small49, 50. The advantage of using data from multiple populations should be discussed from the viewpoint of the costs of genotyping and phenotyping, as pointed out by Muranty et al.46. In the present study, the prediction accuracy was improved by combining the parental and breeding populations. The shorter conserved region of LD in the combined population than in the parental population could improve not only GWAS resolution but also the prediction accuracy by narrowing down the QTL regions. Our results suggest that multiple populations closely related to each other are useful to predict a small variation in the breeding population.
The results of this study suggest that GWAS and GS have a good potential for genetic improvement of fruit quality traits in citrus. Declining sequencing cost enables genomics-assisted breeding with very large numbers of DNA markers, and it has been anticipated that this approach would improve fruit tree breeding by avoiding constraints imposed by the long juvenile period and large plant size51. In the present study, the GWAS power was increased and the prediction accuracy was improved by combining the breeding and parental populations. The results support the idea of breeding-assisted genomics, in which the data collected from actual breeding programs will be beneficial for plant functional genomics16. Because the phenotypic data are accumulated every year, combining marker genotypic data in a breeding program and gathering them will increase the detection power of GWAS and the prediction accuracy of GS. The combination of genomics-based approaches, GWAS and GS, and the data from actual breeding programs will facilitate both functional genomics and fruit tree breeding.
Methods
Plant materials and fruit assessment
A set of 111 citrus varieties (48 hybrid cultivars, 41 breeding/selected strains, 22 indigenous varieties), called the parental population (Supplementary Table S1), and 35 full-sib families with a total of 676 F1 individuals, called the breeding population (Supplementary Table S2), were used in this study. The breeding population was derived from crosses among 45 varieties, of which 41 were included in the parental population. All genetic materials were maintained at NIFTS (Nagasaki and Shizuoka, Japan).
We evaluated 17 fruit quality traits for the parental and breeding populations by using instrumental, sensory, or visual assessment methods (Table 1). Five fruits were sampled from one tree of each genotype in December of each year, when many genotypes were maturing. The mean values obtained from 2008 to 2014 were estimated by fitting a mixed linear model (MLM); year was treated as a fixed effect and variety as a random effect to remove the year effect. The best linear unbiased prediction (BLUP) estimated by the MLM was used for subsequent analysis as the dependent variables of regression models for GWAS and genomic prediction models. The MLM was implemented in the “lmer” function of the R package lme4 ver. 1.1–752. All traits except Weight, Brix, and Acid had ordinal categorical values (Table 1).
SNP genotyping data
DNA was extracted and its quality was evaluated according to Shimizu et al.53. Next-generation sequencing data of 12 citrus varieties was obtained with Illumina HiSeq 2000 in paired-end mode for the development of a SNP Array for genotyping 768 SNPs53, and a SNP array for genotyping 1,536 SNPs was designed from the sequencing data as described by Shimizu et al.53.
SNP genotyping for 768 or 1,536 arrays was performed as described by Shimizu et al.53. Parentage tests were performed using a function of GUGS (General Utilities for Genotyping Study) software (T. Shimizu, in preparation) with known hybrid trios. Finally, 1,841 verified SNPs were obtained (Supplementary Data S1). For further analysis, each of the 1,841 SNP genotypes was converted to 1 (AA homozygotes), −1 (BB homozygotes), or 0 (AB heterozygotes). The rate of missing SNP genotypes was 0.17. We used BEAGLE ver. 3.3.254 to impute the missing genotypes; the mean imputation accuracy (r 2) was 0.97.
Estimation of linkage disequilibrium
To estimate LD between each pair of SNPs within the same chromosome, we calculated the squared correlation coefficients (r 2) of SNP genotypes and plotted them against physical distance between the corresponding markers in Mb. Local polynomial regression with kernel weight was conducted using the “locpoly” function in the R package KernSmooth ver. 2.23–1355 to test the relation between the r 2 values and physical map distances. Physical distances between adjacent markers were 0.056–2,243 kb (mean, 156.4 kb).
Population structure analysis
The genetic structure of the parental population was estimated using hierarchical clustering, ADMIXTURE clustering, and PCA. Hierarchical clustering based on Ward’s method56 with Euclidean distance was conducted by using the R function “hclust”. Model-based clustering implemented in the software ADMIXTURE ver. 1.3.057 infers population structure by estimating individual admixture proportions from multi-locus SNP data by using a maximum-likelihood method. The number of ancestral populations (K) in the parental population varying from 1 to 10 was assumed when using ADMIXTURE. To choose the optimal K value, 5-fold CV was performed. PCA was conducted using the R function “prcomp”. The optimal number of principal components (PCs) in the parental population was determined by estimating the variances of PC scores. To locate the breeding population in the PCA space of the parental population, the PC scores of the breeding population were estimated based on PCA of the parental population. A heat map was generated to estimate the phenotypic population structure of fruit weight (log-converted Weight) by using R package ggplot2 ver. 1.0.058.
Regression models for GWAS
Association analysis was conducted by using an MLM59 implemented in the “GWAS” function of the R package rrBLUP ver. 4.337. To avoid spurious associations due to population structure, a kinship matrix and four PCs were included in the MLM as fixed effects. The kinship matrix was computed by using the “A.mat” function of the R package rrBLUP ver. 4.337. The number of PCs was selected based on the variances of PC scores. The variance of PC score rapidly decreased until PC4, and gradually thereafter (Supplementary Fig. S6). Annotations of the genes containing significant SNPs were obtained from the Phytozome version 12.0.1 (https://phytozome.jgi.doe.gov/pz/portal.html/) and CitrusCyc Pathways version 3.0 databases (http://pathways.citrusgenomedb.org/). The LD heatmaps of the regions surrounding the peaks on Chr. 4 for ColorP and ColorF were constructed by using the R package LDheatmap ver. 0.99–160.
Genomic prediction models
We used 12 methods to evaluate prediction accuracy. A MLM-based method, genomic best linear unbiased prediction (GBLUP), was performed by using the “kinship.BLUP” function of the R package rrBLUP ver. 4.337 with linear ridge kernel regression (RR) and non-linear Gaussian kernel regression (GAUSS). We also used the R package glmnet ver. 1.9–861 for three different linear regression methods: Ridge Regression (alpha = 0), Lasso (alpha = 1), and Elastic Net (alpha = 0.5). The latter is a combination of ridge regression and lasso. A non-linear decision tree-based ensemble learning method, Random Forest, was run in the R package randomForest ver. 4.6–1062. The Bayesian linear regression models Bayesian Ridge Regression (BRR), Bayesian Lasso (BL), BayesA, BayesB, and BayesC were also used for the modeling. These models were implemented in the R package BGLR ver. 1.0.363.
Because 14 of the 17 traits analyzed in this study were scored as ordinal categories (Table 1), seven regression models for the categorical data were also tested. The categorical data was obtained by rounding off the mean continuous values. We used the ordinal probit model-based BayesA and BayesB64, 65, and the R package BGLR for BRR, BL, BayesA, BayesB, and BayesC. The BGLR package supports models for categorical traits.
To evaluate the effect of peak SNPs with high –log10(p) values detected in GWAS, the accuracies of three models were compared. The first model was MLR implemented in the R function “lm”66, 67. The top three peak SNPs with high –log10(p) values of each trait were entered in MLR unless the correlation coefficient between the SNPs was ≥0.6 to prevent multicollinearity. The proportions of the variance explained by the top three peak SNPs for each trait were also estimated by the MLR model. The second model was GBLUP (RR) that treats the effects of the top three SNPs as fixed effects and the effects of other SNPs as random effects. The last model was the commonly used version of GBLUP (RR), which treats all SNPs as random effects.
To take into account the high observed heterozygosity (H o) of the parental population (>0.50)21, a multi-kernel model that considers both additive and dominance genetic effects was compared with a single-kernel model that considers only additive effects. Both models were implemented in the R package of BGLR ver. 1.0.363. The additive relationship matrix (kinship matrix) was computed by the “A.mat” function of the R package rrBLUP, whereas the dominance relationship matrix was calculated as D in equation (6) in Vitezica et al.68 using a modified “A.mat” function. The additive (\({\sigma }_{a}^{2}\)) and dominance (\({\sigma }_{d}^{2}\)) genetic variances and residual variance (\({\sigma }_{e}^{2}\)) were estimated by using the multi-kernel model. Narrow-sense heritability (h 2) of each trait was computed as the ratio of \({\sigma }_{a}^{2}\) to the total phenotypic variance \(({\sigma }_{a}^{2}+{\sigma }_{d}^{2}+{\sigma }_{e}^{2})({h}^{2}={\sigma }_{a}^{2}/({\sigma }_{a}^{2}+{\sigma }_{d}^{2}+{\sigma }_{e}^{2}))\).
To verify the models, we evaluated the prediction accuracy by 10-fold CV using the parental population randomly partitioned into each fold. The CV was repeated 5 times, and the same partition patterns were adapted to all prediction models in each CV. The prediction accuracy was defined as Pearson’s correlation coefficients (r) between observed and predicted genotypic values and regarded as r = 0 at r < 0.
To evaluate the prediction accuracy for the tails of the distribution of fruit weight, we employed the linear ridge kernel regression model GBLUP (RR) and the non-linear Gaussian kernel regression model GBLUP (GAUSS). All varieties except the large- and small-weight groups were used as a training set, whereas the large- and small-weight groups were used as a test set to assess the difficulty of the prediction of the distribution tails. The training set was also used for leave-one-out CV as a control. The prediction accuracy for the distribution tails was also evaluated for other traits. Rank-ordered 4-fold CV of the parental population was performed. The prediction accuracy was calculated in each partition. To show the tails of the distribution, phenotypic variations of the traits were visualized as jitter plots superimposed onto boxplots by using the R packages ggplot2 ver. 1.0.158 and Rmisc ver. 1.569.
To evaluate the prediction accuracy in the breeding population, all 12 methods were applied. Three different training populations for modeling were compared: only the parental population, only the breeding population (with one family excluded), and both the parental and breeding populations combined (with one family excluded); the phenotype of the excluded family was predicted to mimic actual breeding in which the phenotypic information of a family targeted by GS is generally not available. The prediction accuracies for each family or combined all families were calculated.
References
Saunt, J. Citrus varieties of the world. 2nd Ed. (Sinclair Intl. Limited, Norwich, England, 2000).
Economos, C. & Clay, W. D. Nutritional and health benefits of citrus fruits. Food, Nutr. Agric. 24, 11–18 (1999).
Omura, M. & Shimada, T. Citrus breeding, genetics and genomics in Japan. Breed. Sci. 66, 3–17 (2016).
Hodgson, R. W. Horticultural varieties of citrus. in The citrus industry. Vol. 1. (eds Reuther, W., Webber, H. J. & Batchelor, L. D.) 431–591 (University of California Press, Berkeley, USA., 1967).
Cooper, W. C., Reece, P. C. & Furr, J. R. Citrus breeding in Florida - Past, present and future. Proc. Florida State Hort. Soc. 75, 5–13 (1962).
Okudai, N. Recent Trend in breeding medium- and late-maturing citrus in Japan. JARQ, Japan Agric. Res. Q. (1982).
Mitani, N., Matsumoto, R., Yoshioka, T. & Kuniga, T. Citrus hybrid seedlings reduce initial time to flower when grafted onto shiikuwasha rootstock. Sci. Hortic. 116, 452–455 (2008).
Davey, J. W. et al. Genome-wide genetic marker discovery and genotyping using next-generation sequencing. Nat. Rev. Genet. 12, 499–510 (2011).
Brachi, B., Morris, G. P. & Borevitz, J. O. Genome-wide association studies in plants: the missing heritability is in the field. Genome Biol. 12, 232 (2011).
Meuwissen, T. H. E., Hayes, B. J. & Goddard, M. E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829 (2001).
Korte, A. & Farlow, A. The advantages and limitations of trait analysis with GWAS: a review. Plant Methods 9, 29 (2013).
Khan, M. A. & Korban, S. S. Association mapping in forest trees and fruit crops. J. Exp. Bot. 63, 4045–4060 (2012).
Jannink, J. L., Lorenz, A. J. & Iwata, H. Genomic selection in plant breeding: from theory to practice. Brief. Funct. Genomics 9, 166–177 (2010).
Lorenz, A. J. et al. Genomic selection in plant breeding: knowledge and prospects. Adv. Agron. 110, 77–123 (2011).
Grattapaglia, D. & Resende, M. D. V. Genomic selection in forest tree breeding. Tree Genet. Genomes 7, 241–255 (2011).
Poland, J. Breeding-assisted genomics. Curr. Opin. Plant Biol. 24, 119–124 (2015).
Curk, F. et al. Phylogenetic origin of limes and lemons revealed by cytoplasmic and nuclear markers. Ann. Bot. 117, 565–583 (2016).
Heffner, E. L., Sorrells, M. E. & Jannink, J. L. Genomic selection for crop improvement. Crop Sci. 49, 1–12 (2009).
Flint-Garcia, S. A., Thornsberry, J. M. & Buckler, E. S. Structure of linkage disequilibrium in plants. Annu. Rev. Phys. Chem. 53, 319–348 (2002).
Gupta, P. K., Rustgi, S. & Kulwal, P. L. Linkage disequilibrium and association studies in higher plants: Present status and future prospects. Plant Mol. Biol. 57, 461–485 (2005).
Shimizu, T. et al. Hybrid origins of citrus varieties inferred from DNA marker analysis of nuclear and organelle genomes. PLoS One 11(11), e0166969 (2016).
Barnaud, A., Lacombe, T. & Doligez, A. Linkage disequilibrium in cultivated grapevine, Vitis vinifera L. Theor. Appl. Genet. 112, 708–716 (2006).
Calus, M. P. L. & Veerkamp, R. F. Accuracy of breeding values when using and ignoring the polygenic effect in genomic breeding value estimation with a marker density of one SNP per cM. J. Anim. Breed. Genet 124, 362–368 (2007).
Pritchard, J. K. & Przeworski, M. Linkage disequilibrium in humans: models and data. Am. J. Hum. Genet. 69, 1–14 (2001).
van den Berg, I., Boichard, D. & Lund, M. S. Comparing power and precision of within-breed and multibreed genome-wide association studies of production traits using whole-genome sequence data for 5 French and Danish dairy cattle breeds. J. Dairy Sci. 99, 8932–8945 (2016).
de Roos, A. P. W., Hayes, B. J., Spelman, R. J. & Goddard, M. E. Linkage disequilibrium and persistence of phase in Holstein-Friesian, Jersey and Angus cattle. Genetics 179, 1503–1512 (2008).
Yu, Y., Chen, C. & Gmitter, F. G. QTL mapping of mandarin (Citrus reticulata) fruit characters using high-throughput SNP markers. Tree Genet. Genomes 12, 77 (2016).
Kita, M. et al. Cloning and expression of CitPDS1, a gene encoding phytoene desaturase in citrus. Biosci. Biotechnol. Biochem. 65, 1424–1428 (2001).
Kato, M. et al. Accumulation of carotenoids and expression of carotenoid biosynthetic genes during maturation in citrus fruit. Plant Physiol. 134, 824–837 (2004).
Norris, S. R., Barrette, T. R. & DellaPenna, D. Genetic dissection of carotenoid synthesis in arabidopsis defines plastoquinone as an essential component of phytoene desaturation. Plant Cell 7, 2139–2149 (1995).
Brandi, F. et al. Study of ‘Redhaven’ peach and its white-fleshed mutant suggests a key role of CCD4 carotenoid dioxygenase in carotenoid and norisoprenoid volatile metabolism. BMC Plant Biol 11, 24 (2011).
Adami, M. et al. Identifying a carotenoid cleavage dioxygenase (ccd4) gene controlling yellow/white fruit flesh color of peach. Plant Mol. Biol. Report. 31, 1166–1175 (2013).
Piršelová, B. & Matušíková, I. Callose: The plant cell wall polysaccharide with multiple biological functions. Acta Physiol. Plant. 35, 635–644 (2013).
Sakurai, N. & Nevins, D. J. Changes in physical properties and cell wall polysaccharides of tomato (Lycoperskon esculentum) pericarp tissues. Physiol. Plant. 89, 681–686 (1993).
Sakurai, N. & Nevins, D. J. Relationship between fruit softening and wall polysaccharides in avocado (Persea americana Mill) mesocarp tissues. Plant Cell Physiol. 38, 603–610 (1997).
Loulakakis, K. A., Roubelakis-Angelakis, K. A. & Kanellis, A. K. Regulation of glutamate dehydrogenase and glutamine synthetase in avocado fruit during development and ripening. Plant Physiol. 106, 217–222 (1994).
Endelman, J. B. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome J. 4, 250–255 (2011).
Morota, G. & Gianola, D. Kernel-based whole-genome prediction of complex traits: A review. Front. Genet 5, 1–13 (2014).
Xu, S., Zhu, D. & Zhang, Q. Predicting hybrid performance in rice using genomic best linear unbiased prediction. Proc. Natl. Acad. Sci. USA 111, 12456–12461 (2014).
Zhao, Y., Zeng, J., Fernando, R. & Reif, J. C. Genomic prediction of hybrid wheat performance. Crop Sci. 53, 802–810 (2013).
Wellmann, R. & Bennewitz, J. Bayesian models with dominance effects for genomic evaluation of quantitative traits. Genet. Res. 94, 21–37 (2012).
Wu, G. A. et al. Sequencing of diverse mandarin, pummelo and orange genomes reveals complex history of admixture during citrus domestication. Nat. Biotechnol. 32, 656–662 (2015).
Xu, Q. et al. The draft genome of sweet orange (Citrus sinensis). Nat. Genet. 45, 59–66 (2013).
Pszczola, M., Strabel, T., Mulder, H. A. & Calus, M. P. L. Reliability of direct genomic values for animals with different relationships within and to the reference population. J. Dairy Sci. 95, 389–400 (2012).
Kumar, S. et al. Genomic selection for fruit quality traits in apple (Malus × domestica Borkh.). PLoS One 7(5), e36674 (2012).
Muranty, H. et al. Accuracy and responses of genomic selection on key traits in apple breeding. Hortic. Res. 2, 15060 (2015).
Fodor, A. et al. Genome-wide prediction methods in highly diverse and heterozygous species: Proof-of-concept through simulation in grapevine. PLoS One 9(11), e110436 (2014).
Zhao, Y. et al. Accuracy of genomic selection in European maize elite breeding populations. Theor. Appl. Genet. 124, 769–776 (2012).
Ibanez-Escriche, N., Fernando, R. L., Toosi, A. & Dekkers, J. C. Genomic selection of purebreds for crossbred performance. Genet. Sel. Evol. 41, 12 (2009).
de Roos, A. P. W., Hayes, B. J. & Goddard, M. E. Reliability of genomic predictions across multiple populations. Genetics 183, 1545–1553 (2009).
Iwata, H., Minamikawa, M. F., Kajiya-Kanegae, H., Ishimori, M. & Hayashi, T. Genomics-assisted breeding in fruit trees. Breed. Sci. 66, 100–15 (2016).
Bates, D., Maechler, M., Bolker, B. & Walker, S. lme4: Linear mixed-effects models using Eigen and S4. R package version 1.1–7. http://cran.r-project.org/package=lme4 (2014).
Shimizu, T. et al. A genomic approach to selecting robust and versatile SNP sets from next-generation sequencing data for genome-wide association study in citrus cultivars. Acta Hortic. 1135, 23–32 (2016).
Browning, B. L. & Browning, S. R. A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals. Am. J. Hum. Genet. 84, 210–223 (2009).
Wand, M. P. & Jones, M. C. Kernel smoothing. (Chapman & Hall, 1995).
Ward, J. H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 58, 236–244 (1963).
Alexander, D. H., Novembre, J. & Lange, K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 19, 1655–1664 (2009).
Wickham, H. ggplot2: Elegant Graphics for Data Analysis. (Springer, 2009).
Yu, J. et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 38, 203–208 (2006).
Shin, J.-H., Blay, S., McNeney, B. & Graham, J. LDheatmap: An R Function for Graphical Display of Pairwise Linkage Disequilibria between Single Nucleotide Polymorphisms. J. Stat. Softw. 16, 1–10 (2006).
Friedman, J., Hastie, T. & Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33, 1–22 (2010).
Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).
Perez, P. BGLR: A statistical package for whole genome regression and prediction. Genetics 198, 483–495 (2014).
Iwata, H., Ebana, K., Fukuoka, S., Jannink, J. L. & Hayashi, T. Bayesian multilocus association mapping on ordinal and censored traits and its application to the analysis of genetic variation among Oryza sativa L. germplasms. Theor. Appl. Genet. 118, 865–880 (2009).
Iwata, H. et al. Potential assessment of genome-wide association study and genomic selection in Japanese pear Pyrus pyrifolia. Breed. Sci. 63, 125–140 (2013).
Chambers, J. M. Linear models. in Statistical Models in S. (eds Chambers, J. M. & Hastie, T. J.) 95–144 (Wadsworth & Brooks/Cole, 1992).
Wilkinson, G. N. & Rogers, C. E. Symbolic descriptions of factorial models for analysis of variance. J. R. Stat. Soc. Ser. C (Applied Stat.) 22, 392–399 (1973).
Vitezica, Z. G., Varona, L. & Legarra, A. On the additive and dominant variance and covariance of individuals within the genomic selection scope. Genetics 195, 1223–1230 (2013).
Hppe, R. M. Rmisc: Ryan miscellaneous. R package version 1.5. https://cran.r-project.org/package=Rmisc (2013).
Acknowledgements
This research was supported by a grant from the Ministry of Agriculture, Forestry and Fisheries of Japan (Genomics-based Technology for Agricultural Improvement, NGB-1006, 2009 and 2010) and was partially supported by the Transdisciplinary Research Integration Center Project of the Research Organization of Information and Systems (ROIS), Japan. Data analysis was partially performed using the ROIS NIG Supercomputer System.
Author information
Authors and Affiliations
Contributions
M.F.M., K.N., T.S., and H.I. conceived and designed the study. K.N., T.Y., A.I., and H.H. performed phenotyping. S.G. and T.S. extracted DNA. T.S. and E.K. designed the SNP genotyping array. E.K., S.G., S.M., Y.K., A.T., A.F., Y.N., and T.S performed SNP genotyping. M.F.M., H.K.K., A.O., T.H., and H.I. performed genomic prediction and genome-wide association study. M.F.M., K.N., and T.S. wrote the original manuscript. K.N., H.K.K., A.O., T.S., and H.I. helped to edit the manuscript. All authors read and approved the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Minamikawa, M.F., Nonaka, K., Kaminuma, E. et al. Genome-wide association study and genomic prediction in citrus: Potential of genomics-assisted breeding for fruit quality traits. Sci Rep 7, 4721 (2017). https://doi.org/10.1038/s41598-017-05100-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-05100-x
This article is cited by
-
Comprehensive genome-wide identification and transferability of chromosome-specific highly variable microsatellite markers from citrus species
Scientific Reports (2023)
-
Genomic region and origin for selected traits during differentiation of small-fruit cultivars in Japanese apricot (Prunus mume)
Molecular Genetics and Genomics (2023)
-
Comparative transcriptomics of wild and commercial Citrus during early ripening reveals how domestication shaped fruit gene expression
BMC Plant Biology (2022)
-
Comprehensive mechanistic insights into the citrus genetics, breeding challenges, biotechnological implications, and omics-based interventions
Tree Genetics & Genomes (2022)
-
Efficient method for generating citrus hybrids with polyembryonic Satsuma mandarin as the female parent
Molecular Breeding (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.