Abstract
Two-dimensional systems have strengthened their position as a key materials for novel applications. Very recently, boron joined the distinguished group of elements confirmed to possess 2D allotropes, named borophenes. In this work, we explore the stability and hardness of the highest borides of tungsten, which are built of borophenes separated by metal atoms. We show that the WB3+x compounds have Vickers hardnesses approaching 40 GPa only for small values of x. The insertion of extra boron atoms is, in general, detrimental to the hardness of WB3 because it leads to the formation of quasi-planar boron sheets that are less tightly connected with the adjacent tungsten layers. Very high concentrations of boron (x ≈ 1), give rise to a soft (Vickers hardness of ~8 GPa) and unstable hP20-WB4 structure that can be considered to be built of quasi-planar boron α-sheets separated by graphitic tungsten layers. By contrast, we show that the formation of tungsten vacancies leads to structures, e.g. W0.75B3+x , with Vickers hardnesses that are not only similar in value to the experimentally reported load-independent hardnesses greater than 20 GPa, but are also less sensitive to variations in the boron content.
Similar content being viewed by others
Introduction
The highest boride of tungsten–often referred to as tungsten tetraboride–is recently best explored for its potential applications as superhard material, however made its first appearance in the literature in 1961, when Chretien and Helgorsky1 did the first attempt to find its structure. Years later Romans and Krug2 reported that WB4 has a hexagonal structure of 20 atoms per unit cell and lattice constants of 5.2 and 6.34 Å for a and c, respectively. The space group of this structure was determined to be P63/mmc. The hP20-WB4 structure serves now as a reference structure for almost all subsequent experimental studies related to boron-rich materials with a WB4-like structure3,4,5,6,7. The mechanical properties of WB4 were first determined by Gu et al.3 who reported Vickers hardness (H V) values of 46.2 and 31.8 GPa under applied loads of 0.49 and 4.90 N, respectively, measured by the microindentation technic. Subsequently, Mohammadi et al.5 also measured the hardness by microindentation method and reported H V values of 43.3 and 28.1 GPa at low (0.49 N) and high (4.90 N) loads, respectively. More recently, the Vickers hardness for W0.85B3 was reported by Tao et al.8 to be 42.0 and 25.5 GPa under applied loads of 0.098 and 4.90 N, respectively. Finally, Lech et al.9 determined the maximum nanoindentation hardness of W0.82B3.54 (at a penetration depth of 95.25 nm) to be 41.7 GPa. It is generally accepted that a reliable hardness of a material can be determined from the asymptotic hardness region achieved at high loads10. The quite large differences between the H V values reported for WB4, especially for high loads, can be attributed to differences in the amount of boron contamination and/or presence of tungsten vacancies, which were experimentally seen in the studied samples9. By exploring structures with different compositions, we are able to explain on the theoretical ground the apparent differences between the reported experimental results.
The common description of hP20-WB4 that can be found in the literature is that this structure consists of graphitic boron layers separated by graphitic layers of W atoms like in the hP16-WB3 structure but with additional B2 dimers located between boron sheets and aligned along the c-axis (see Fig. 1a). This description, although very elegant, is completely decoupled from more recent investigations related to 2D boron crystals11, 12. An ‘updated’ view to hP20-WB4 would be that it is a structure consisting of a sequence of quasi-planar boron α-sheets (see Fig. 1b) separated by graphitic W layers. Extensive theoretical investigations have proved, however, that the stoichiometric WB4 compound in the hP20-WB4 structure would be thermodynamically and dynamically unstable. Its calculated enthalpy of formation is positive, with a value of 0.4 eV/atom13, and from its phonon dispersion the structure was shown to be highly unstable14. In fact, we argue that the formation of stable quasi-planar boron layers within the hP20-WB4 structure is the main reason for the instability of this and related boron-rich structures. Thus, from this viewpoint, the experimentally obtained WB4 compounds cannot adopt the hP20-WB4 structure.
(a) The hP20-WB4 structure. The large and small spheres represent tungsten and boron atoms, respectively. (b) The side and top views of the buckled boron α-sheet present in the hP20-WB4 structure. (c) The hP16-WB3 structure. The small red dots indicate the position of the four extra boron atoms that are present in the hP20-WB4 structure. (d) The hP16-B structure that is obtained by removing all of the tungsten atoms from hP20-WB4. The numbers on the structures represent the nearest neighbor B–B distances and are given in angstroms.
In more recent reports13, 15, the highest borides of tungsten are described as hP16-WB3 structures contaminated with additional boron atoms. The exact position of the boron atoms in the crystal lattice are difficult to be determined experimentally because of the large mass difference between W and B atoms15. Therefore, the combination of theory and experiment is essential for the understanding of the observed findings. Since in the experiment WB3 is not only contaminated with boron atoms but also, to some extent, possesses tungsten vacancies8, 9, 16, in this work a more precise notation is used when referring to the highest boride of tungsten, namely W1–y B3+x , to underline the existence of W vacancies and explore their influence on the stability and properties of WB3+x .
Results
The structure of W1–y B3+x
The highest borides of tungsten are obtained starting from WB3 in the hP16-WB3 structure by adding additional boron atoms at the positions shown in red in Fig. 1c and/or by selective removal of W atoms. The fully ‘packed’ structure is the hP20-WB4 structure, shown in Fig. 1a, that has buckled boron α-sheets, shown in Fig. 1b, separated by W layers. The buckling height is 1.49 Å and is larger than that of the freestanding triangular boron sheet (0.82 Å)17. The complete removal of all the W atoms from hP20-WB4 leads to the all-boron structure that consists of 16 atoms per unit cell and is shown in Fig. 1d. This structure is nothing more than a sequence of quasi-planar boron α-sheets arranged in such a way that the boron atoms that stick out of the graphitic frames face each other forming dimers. We can describe the hP20-WB4 structure in the same manner except that the boron α-sheets are intercalated by tungsten layers. The hP16-B structure is less stable than the α-rhombohedral boron (hR12-B) by 0.47 eV/atom. Interestingly enough, by removing one of the boron dimers in hP16-B a slightly more stable (by 12 meV/atom) hP14-B structure is obtained. The hP16-B and hP14-B structures have P63/mmc and P6/mmc space groups, respectively, and a = 5.034 Å, c = 6.166 Å and a = 5.081 Å, c = 5.195 Å lattice constants, respectively.
Stability of the compounds
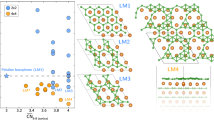
To explore the relative stability of the generated structures, we calculate for each structure its enthalpy of formation per atom, ΔE. The ΔE values are calculated relative to the enthalpies of tungsten and boron solids in the body-centered cubic (cI2-W) and α-rhombohedral (hR12-B) structures, respectively. The results for ΔE versus boron atomic content, (3 + x)/(4 + x − y), are summarized in Fig. 2a and b. All the structures that have enthalpies of formation above the horizontal dashed lines in Fig. 2a and b are, in principle, thermodynamically unstable. It is instructive, however, to draw also a line that connects cI2-W with hP16-B, what is shown in Fig. 2a and b by a dashed line that is above the horizontal dashed line. The enthalpies of formation of almost all the considered W1–y B3+x structures are located bellow the cI2-W ↔ hP16-B line. This means that the incorporation of W atoms in between boron sheets is energetically favorable. The enthalpies of formation versus boron atomic content are presented in two ways. In Fig. 2a, we organize the results according to the number of extra boron atoms, n B, in W1–y B3+x relative to hP16-WB3. In Fig. 2b, the same results have been organized emphasizing the number of W vacancies in W1–y B3+x also relative to hP16-WB3. It is clear from Fig. 2a that negative enthalpies of formation or positive ΔE but close to 0, have structures with none or no more than 2 extra B atoms. The cases with 3 and 4 extra B atoms have ΔE \(\simeq \) 0.2 eV/atom or larger. This also includes the highly debated hP20-WB4 structure (ΔE = 0.36 eV/atom). From Fig. 2b, we can learn that the only relevant cases are those for which the number of W vacancies, n V(W), is 0 or 1, since among those cases we can find structures with negative or close to 0 enthalpies of formation. Combining all the information coming from Fig. 2, we choose 8 structures that in principle can be important to understand experimental results. Six of those structures are shown in Fig. 3. For each relevant boron atomic content, we choose the structure with the lowest enthalpy of formation. The relevant structures (the highest boride of tungsten) are those with boron contents ranging from 0.75 (WB3) to 0.83 (W0.75B3.75). The highest boron content is chosen following ref. 9.
Enthalpies of formation for structures derived from hP16-WB3 by selective removal of tungsten atoms and/or contamination by additional boron atoms. (a) and (b) Show the same results organized in two different ways described in the text. The vertical dotted lines are drawn as guide to the eye and correspond to selective boron atomic contents. The horizontal dashed line and the line that is above represent cI2-W ↔ hP12-B and cI2-W ↔ hP16-B lines, respectively.
The lattice constants and symmetry of the structures shown in Fig. 3 are summarized in Table 1. In this table, we also include, for each structure, the occupations of the B and W atoms relative to the P63/mmc space group. It is important to notice that if we take the average of all the lattice constants listed in Table 1, we get 5.192 and 6.303 Å for a and c, respectively, that is, values that match quite well those reported in the experiment (5.2 and 6.34 Å for a and c, respectively)9. This may suggest that in the experiment is observed a non-stoichiometric structure with a random distribution of both the extra boron atoms and W vacancies and may farther explain the difficulties in the interpretations of X-ray and neutron diffraction data9.
Mechanical properties of the compounds
The elastic properties of the studied structures are summarized in Table 2, whereas the plot of the Vickers hardness versus boron atomic content is shown in Fig. 4. From this figure, we see that only stoichiometric WB3 (hP16-WB3+x ) can be considered as superhard material. The hardness is however affected by contamination by extra B atoms. This is clearly seen in Fig. 4 for WB3+x , for which the Vickers hardness changes from ~40 to ~8 GPa for an increase of the B content by 5%. For the tungsten-deficient W0.75B3+x structures the picture is different, namely, we obtain smaller variations of the Vickers hardness with the increase of B content (see Fig. 4). Most of the considered structures have Vickers hardnesses larger or equal to 20 GPa, what means that the highest boride of tungsten is a hard material but not superhard (at least in the range of considered boron contents). A particularly soft structure is hP20-WB4, which has a comparable bulk modulus to that of hP16-WB3 but much smaller shear modulus (see Table 2). The softening of WB4 may be attributed to the formation of stable 2D boron layers (α-sheets) which are less tightly bound to the tungsten layers. The average nearest neighbor W–B distance is 2.324 and 2.383 Å in WB3 and WB4, respectively, what reflects the weakening of the W–B bond in WB4 with respect to WB3.
Vickers hardnesses calculated for the most stable structures at a given boron atomic content. The filled and open squares correspond to WB3+x and W0.75B3+x compounds, respectively. The structures of WB3+x are shown in Fig. 1a and c, and Fig. 3a and b, whereas the structures of W0.75B3+x are shown in Fig. 3c–f.
Another way of explaining the lack of stability of the hP20-WB4 structure could be by using the concept of self-doping in boron sheets introduced in ref. 18. By adding extra boron atoms to the hP16-WB3 structure, we essentially transfer extra negative charge into the boron graphitic layers present in hP16-WB3. This extra charge influences the B–B distances in these layers. In Fig. 1a,c, and d, we show the B–B nearest neighbor distances between boron atoms for the structures present there. The B–B distances (1.739 Å and 1.794 Å) for the in-plane boron atoms in hP20-WB4 are clearly longer than the respective B–B distances (1.708 Å and 1.732 Å) in hP16-WB3. This means that the graphitic layers in hP20-WB4 are overcharged with electrons. Also the inclusion of tungsten atoms into the hP16-B structure seems to do the same effect as boron doping, since the B–B distances (1.696 Å and 1.669 Å) for the in-plane atoms in hP16-B are shorter than the respective distances in hP20-WB4. The out-of-plane boron atoms in hP20-WB4 stay as distant as possible from the graphitic boron layers in order to minimize the transfer of negative charge to the in-plane boron atoms. As a consequence, we have a formation of B2 dimers that are loosely bound to the graphitic frames.
In summary, we show that the insertion of extra boron atoms into the WB3 structure is, in general, energetically unfavorable and lowers its shear modulus while maintaining a high value for the bulk modulus, effectively leading to a softer material. A high degree of boron contamination leads to the formation of quasi-planar boron α-sheets separated by graphitic tungsten layers in WB4. Structures of the W1−y B3+x type, in which boron contamination is accompanied by the presence of tungsten vacancies, are more stable and harder than WB4. Finally, the formation of tungsten vacancies gives rise to structures (e.g. W0.75B3+x ) with Vickers hardnesses that are less sensitive to variations in the boron content and are similar in value to the experimentally reported load-independent values, which are greater than 20 GPa. Our results should provide guidance for the development of new WB4 synthesis strategies.
Methods
Our first principles calculations were based on density functional theory (DFT) and the projector augmented wave (PAW) method as implemented in the Quantum ESPRESSO simulation package19. For the exchange and correlation functional, we used the revised Perdew-Burke-Ernzerhof spin-polarized generalized gradient approximation (PBEsol-GGA) functional. The plane-wave basis set was converged using a 40 Ry energy cutoff. A 8 × 8 × 8 k-point mesh and a Gaussian smearing of 0.005 Ry was used in the Brillouin zone integration. The calculations were carried out using supercells containing up to 20 atoms. For each considered structure, a full atomic position and lattice parameter relaxation was preformed.
A total of 60 low-energy W1−y B3+x structures with high boron atomic content were selected using the cluster-expansion method implemented in the Alloy-Theoretic Automated Toolkit (ATAT)20. The enthalpies of formation were calculated from the formula: \({\rm{\Delta }}E={E}_{{\rm{t}}{\rm{o}}{\rm{t}}}({{\rm{W}}}_{1-y}{{\rm{B}}}_{3+x})-(1-c){E}_{{\rm{t}}{\rm{o}}{\rm{t}}}(\text{W solid})-c{E}_{{\rm{t}}{\rm{o}}{\rm{t}}}(\text{B solid})\), where E tot are the calculated total energies per atom and c = (3 + x)/(4 + x − y) is the boron atomic content. The elastic properties of the most stable structures were calculated using the ElaStic code21. To compute the Vickers hardness, we used the semi-empirical hardness model proposed by Chen et al.22 that correlates hardness with the elastic properties of the material. According to this model the expression for hardness is \({H}_{{\rm{V}}}=\mathrm{2(}{k}^{2}G{)}^{0.585}-3\), where G and k are the shear modulus and the Pugh modulus ratio (k = G/B, where B is the bulk modulus), respectively.
References
Chretien, A. & Helgorsky, J. Borides of molybdenum and tungsten, MoB4 and WB4; new compounds. Compt. Rend. 252, 742–744 (1961).
Romans, P. A. & Krug, M. P. Composition and crystallographic data for the highest boride of tungsten. Acta Crystallogr. 20, 313–315, doi:10.1107/S0365110X6600063X (1966).
Gu, Q., Krauss, G. & Steurer, W. Transition metal borides: Superhard versus ultra-incompressible. Adv. Mater. 20, 3620–3626, doi:10.1002/adma.200703025 (2008).
Liu, C. et al. Low-compressibility of tungsten tetraboride: a high pressure X-ray diffraction study. High Pres. Res. 31, 275–282, doi:10.1080/08957959.2011.582871 (2011).
Mohammadi, R. et al. Tungsten tetraboride, an inexpensive superhard material. Proc. Natl. Acad. Sci. USA 108, 10958–10962, doi:10.1073/pnas.1102636108, http://www.pnas.org/content/108/27/10958.abstract (2011).
Xie, M. et al. Exploring the high-pressure behavior of superhard tungsten tetraboride. Phys. Rev. B 85, 064118, doi:10.1103/PhysRevB.85.064118 (2012).
Xiong, L. et al. Radial x-ray diffraction of tungsten tetraboride to 86 GPa under nonhydrostatic compression. J. Appl. Phys. 113, 033507, doi:10.1063/1.4775482 (2013).
Tao, Q. et al. Exploring hardness and the distorted sp 2 hybridization of B–B bonds in WB3. Chem. Mater. 26, 5297–5302, doi:10.1021/cm5021806 (2014).
Lech, A. T., Turner, C. L., Mohammadi, R., Tolbert, S. H. & Kaner, R. B. Structure of superhard tungsten tetraboride: A missing link between MB2 and MB12 higher borides. Proc. Natl. Acad. Sci. USA 112, 3223–3228, doi:10.1073/pnas.1415018112 (2015).
Tian, Y., Xu, B. & Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Metal Hard Mater. 33, 93–106, doi:10.1016/j.ijrmhm.2012.02.021 (2012).
Tang, H. & Ismail-Beigi, S. Novel precursors for boron nanotubes: The competition of two-center and three-center bonding in boron sheets. Phys. Rev. Lett. 99, 115501, doi:10.1103/PhysRevLett.99.115501 (2007).
Feng, B. et al. Experimental realization of two-dimensional boron sheets. Nat. Chem. 8, 563–568, doi:10.1038/nchem.2491 (2016).
Cheng, X.-Y., Chen, X.-Q., Li, D.-Z. & Li, Y.-Y. Computational materials discovery: the case of the W–B system. Acta Crystallogr. C 70, 85–103, doi:10.1107/S2053229613027551 (2014).
Zhang, R. F. et al. Stability and strength of transition-metal tetraborides and triborides. Phys. Rev. Lett. 108, 255502, doi:10.1103/PhysRevLett.108.255502 (2012).
Cheng, X. et al. Interstitial-boron solution strengthened WB 3+x . Appl. Phys. Lett. 103, 171903, doi:10.1063/1.4826485 (2013).
Zeiringer, I. et al. Crystal structure of W1−x B3 and phase equilibria in the boron-rich part of the systems Mo-Rh-B and W-{Ru,Os,Rh,Ir,Ni,Pd,Pt}-B. J. Phase Equilibria Diffus 35, 384–395, doi:10.1007/s11669-014-0291-0 (2014).
Kunstmann, J. & Quandt, A. Broad boron sheets and boron nanotubes: An ab initio study of structural, electronic, and mechanical properties. Phys. Rev. B 74, 035413, doi:10.1103/PhysRevB.74.035413 (2006).
Tang, H. & Ismail-Beigi, S. Self-doping in boron sheets from first principles: A route to structural design of metal boride nanostructures. Phys. Rev. B 80, 134113, doi:10.1103/PhysRevB.80.134113 (2009).
Giannozzi, P. et al. Quantum Espresso: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502, http://stacks.iop.org/0953-8984/21/i=39/a=395502, doi:10.1088/0953-8984/21/39/395502 (2009).
van de Walle, A., Asta, M. & Ceder, G. The alloy theoretic automated toolkit: A user guide. Calphad 26, 539–553, doi:10.1016/S0364-5916(02)80006-2, http://www.sciencedirect.com/science/article/pii/S0364591602800062 (2002).
Golesorkhtabar, R., Pavone, P., Spitaler, J., Puschnig, P. & Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comput. Phys. Commu. 184, 1861–1873, doi:10.1016/j.cpc.2013.03.010, http://www.sciencedirect.com/science/article/pii/S0010465513001070 (2013).
Chen, X.-Q., Niu, H., Li, D. & Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 19, 1275–1281, doi:10.1016/j.intermet.2011.03.026, http://www.sciencedirect.com/science/article/pii/S0966979511000987 (2011).
Acknowledgements
The author gratefully acknowledges the support of the National Science Centre (NCN) through grant UMO-2013/11/B/ST3/04273 and the access to the computing facilities of the Interdisciplinary Center of Modeling at the University of Warsaw.
Author information
Authors and Affiliations
Contributions
N.G.Sz. did the calculations and analysis, wrote and reviewed the manuscript, and prepared all of the Figures.
Corresponding author
Ethics declarations
Competing Interests
The author declares that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gonzalez Szwacki, N. The structure and hardness of the highest boride of tungsten, a borophene-based compound. Sci Rep 7, 4082 (2017). https://doi.org/10.1038/s41598-017-04394-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-04394-1
This article is cited by
-
Damage analysis of a perfect broadband absorber by a femtosecond laser
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.