Abstract
The introduction of mild cognitive impairment (MCI) as a diagnostic category adds to the challenges of diagnosing Alzheimer’s Disease (AD). No single marker has been proven to accurately categorize patients into their respective diagnostic groups. Thus, previous studies have attempted to develop fused predictors of AD and MCI. These studies have two main limitations. Most do not simultaneously consider all diagnostic categories and provide suboptimal fused representations using the same set of modalities for prediction of all classes. In this work, we present a combined framework, cascaded multiview canonical correlation (CaMCCo), for fusion and cascaded classification that incorporates all diagnostic categories and optimizes classification by selectively combining a subset of modalities at each level of the cascade. CaMCCo is evaluated on a data cohort comprising 149 patients for whom neurophysiological, neuroimaging, proteomic and genomic data were available. Results suggest that fusion of select modalities for each classification task outperforms (mean AUC = 0.92) fusion of all modalities (mean AUC = 0.54) and individual modalities (mean AUC = 0.90, 0.53, 0.71, 0.73, 0.62, 0.68). In addition, CaMCCo outperforms all other multi-class classification methods for MCI prediction (PPV: 0.80 vs. 0.67, 0.63).
Similar content being viewed by others
Introduction
Alzheimer’s Disease (AD) is the most prevalent type of dementia in the US, and is primarily characterized by irreversible cognitive decline associated with neurodegeneration1. On account of an increasing aging population in the US, the annual incidence of AD is expected to double by 20502. However, studies have shown that the number of cases in 2050 can be reduced by 50% if the average age at the onset of the disease could be delayed by 5 years3. This may be achieved by early diagnosis and intervention with treatments that delay disease progression.
The original diagnostic criteria, known as NINCDS-ADRDA criteria, qualitatively combined information from medical history, clinical examination, neurophysiological testing and laboratory assessments to provide a sensitivity of 81% and a specificity of 70% for AD diagnosis4. In an attempt to diagnose AD earlier, the revised criteria now include two major changes: (i) addition of an intermediate diagnostic group, mild cognitive impairment (MCI) as well as (ii) guidelines for interpretation of imaging and molecular markers1. The intermediate diagnostic category, MCI, comprises of a heterogeneous group of patients who present early symptoms of cognitive impairment which do not interrupt daily life. While some MCI patients progress to AD over time, some remain stable while a few even regress back to healthy states. Given that MCI patients are at a greater risk for AD, there is an opportunity for early diagnosis of AD by identifying the subpopulation of MCI patients who progress to AD. However, to move toward this opportunity, the most immediate challenge is to accurately distinguish MCI from both HC and AD. The new diagnostic criteria therefore includes recommendations for incorporation of alternate biomarkers that have previously shown promise in predicting presymptomatic disease5.
Alongside recent developments in imaging and molecular diagnostic technologies, several studies have sought to identify biomarkers of AD. Cerebrospinal fluid (CSF) markers in particular have been extensively studied6,7,8 on account of their direct relationship with pathological characteristics of the disease such as amyloid burden and neuronal degeneration. On the genetic front, apolipoprotein E (ApoE) has been established as an indicator of risk for AD9. Structural information on 1.5 Tesla T1w Magnetic Resonance Imaging (MRI)10 such as hippocampal volume and functional information on [18F] fluorodeoxyglucose uptake (FDG-PET)11 such as changes in glucose metabolism have previously shown to be predictive of AD. Availability of multiple, complementary markers and data streams now presents an opportunity to combine different sources of information in order to potentially improve the ability to predict AD early, prior to its onset. However, qualitatively combining the vast amount of information is challenging and likely to result in subjective interpretations. On the other hand, quantitative approaches to identification of fused biomarkers is challenged by differences in data dimensionality, small sample size of most biomedical datasets and by the increase in data dimensionality associated with combining multiscale data12,13,14,15.
Several methods have previously been developed and explored to quantitatively combine multiscale biomedical data. Most data fusion approaches can generally be categorized based on the level at which information is combined: (i) raw data level (low level fusion), (ii) feature level (intermediate level fusion) or (iii) decision level (high level fusion)16. Data integration at the raw data level is limited to homogeneous data sources and is thus not directly applicable for fusion of multiscale, biomedical data. Alternatively, decision level strategies17 bypass challenges associated with fusion of heterogeneous data types by combining independently derived decisions from each data source. In doing so, relationships between the different data channels remain largely unexploited14, 15.
Most previous work in prediction of AD employ feature level integration where raw data is first converted into quantitative feature representations which are then combined using concatenation-based18, 19, kernel-based20, 21, manifold-based22 and most recently deep learning-based23, 24 methods. A brief summary of select related previous work is provided in Table 1. While feature concatenation18, 19 provides a simple method for investigating the added predictive value of each modality, it is sub-optimal for combining modalities with significantly different dimensionalities as modalities with larger feature sets are likely to dominate the joint-representation and hence the fused predictor12. Kernel-based and manifold-based methods20,21,22 alternatively transform raw data from the original space to a high dimensional embedding space where the different data types are more homogeneously represented, thereby making them more amenable for fusion. However, such methods are prone to overfitting25, 26 particularly given the small sample sizes of most biomedical datasets and the noise associated with each of the biomedical data sources which, if unaccounted for, may drown the increase in signal achievable by fusion. Suk et al.23 and Liu et al.24 presented deep learning based fusion approaches which seek to learn integrated structural and functional feature representations from MRI and PET. However, the method is limited to fusion of spatially aligned imaging data. In addition, deep learning methods generally require very large datasets in order to model complex non-linear relationships via several hidden layers. This could very easily result in overfitting on datasets with small sample size, especially in the presence of noise.
Regardless of the fusion strategy employed, most previous studies evaluate their methods by simplifying the multiclass problem (HC vs. MCI vs. AD) into the following binary classification tasks – AD vs. HC, MCI vs. HC. Recent work24 showed that multiclass classification resulted in significantly lower predictive performance as compared to that of the aforementioned binary classification tasks, suggesting that all the diagnostic classes must be considered to estimate the performance of a proposed model in a clinical setting. Generally, there are three common methods for multiclass classification – one vs. another, one vs. all (OVA) and one shot classification (OSC). For classification task with \({\mathscr{C}}=\{{c}_{1},{c}_{2},\ldots {c}_{n}\}\) classes, the one vs. another classifier attempts to independently solve binary class problems c i vs. c j , \(i\ne j\) arising from all pairwise combinations of classes. With this strategy, it is unclear how to combine results from the multiple binary problems in order to then determine the overall classifier performance. Alternatively, OVA seeks to solve c i vs {c j }, j = 1 … n, \(j\ne i\), while OSC attempts to simultaneously solve c 1 vs. c 2 vs. … vs. c n . OVA may not be able to appropriately classify intermediate classes such as MCI where the ‘all’ category comprises of data points that lie on either extrema of disease spectrum (i.e. healthy and AD). While OSC, which classifies multiple classes at once, overcomes the aforementioned limitations of the other two strategies, it assumes that the same set of modalities are optimal for separating all classes. When addressing multiclass problem in the context of data fusion, it may not be realistic to expect the same combination of modalities to be the most informative for all the various classes. In addition, some classification tasks may require information from fewer modalities to provide sufficiently accurate information while other, more challenging tasks may require additional information.
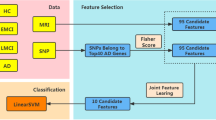
In this work, we introduce the cascaded multiview canonical correlation (CaMCCo) framework which brings together three different unique ideas; data fusion approach, modality selection concept and a cascaded classification scheme. The CaMCCo approach is employed in this paper for the problem of AD diagnosis. CaMCCo seeks to fuse a subset of modalities from T1w MRI, FDG PET, ApoE, CSF, plasma proteomics and neurophysiological exam scores in order to optimize classifier performance at each level of the cascade (Fig. 1). For data fusion, CaMCCo employs supervised multiview canonical correlation analysis (sMVCCA)27, 28 which provides a common, low dimensional representation that is discriminative of classes and allows for combining any number of heterogeneous forms of multidimensional, multimodal data. The fusion scheme operates under the assumption that information overlap increases with increasing number of data sources or ‘views’ as all views fundamentally capture information pertaining to the same object. As such, it seeks to maximize correlations between modalities and with class labels.
The cascade and the modalities for fusion at each level of the cascade were determined on training set and validated on independent testing set. Neurophysiological test scores (ADAS-Cog) are fused with CSF proteomics and APOE at the first level of the cascade to identify healthy controls (HC). At the second level, ADAS-Cog scores are combined with PET to distinguish between patients with Alzheimer’s Disease (AD) and mild cognitive impairment (MCI).
Previous work27, 28 has shown the application of sMVCCA in the context of predicting prostate cancer prognosis where sMVCCA based fusion of histologic and proteomic features was found to be more discriminative of classes as compared to individual modalities as well as several fused representations including LDA, CCA, MVCCA, PCA, regularized CCA (RCCA), supervised regularized CCA (SRCCA), and generalized embedding concatenation (GEC). Although sMVCCA is able to fuse any number of modalities, the practicality of its application in a clinical setting where the trade-off between added improvement in performance and increased burden of additional tests must be leveraged29. CaMCCo therefore extends on previous work to address clinical challenges associated with AD diagnosis by employing the fusion methodology within cascaded classification framework where only a subset of modality(ies) that maximize the performance for each classification task are fused at each level of cascade. Unlike most prior applications of multiclass classification methods to AD diagnosis, CaMCCo simultaneously considers all diagnostic classes via its cascaded classification approach. Unlike most prior applications of data fusion methods for AD diagnosis, CaMCCo seeks to identify, selectively retain and combine only the most informative data source(s) for each class label. As shown in Fig. 1, each patient is first classified as being healthy or cognitively impaired (CI) using ADAS-Cog score, CSF and APOE. If classified as CI, the ADAS-Cog and PET are used to distinguish between MCI and AD cases.
Methods
Supervised Multiview Canonical Correlation Analysis for Data Fusion
We apply supervised Multiview Canonical Correlation Analysis (sMVCCA)27, 28, an extension of canonical correlation analysis (CCA) and multiview canonical correlation analysis (MVCCA)30, to obtain a low-dimensional, shared representation of the modalities of interest. CCA31 is a linear dimensionality reduction method commonly used for data fusion as it accounts for relationships between two sets of input variables. MVCCA generalizes CCA by finding the linear subspace where pairwise correlations between multiple (more than two) modalities can be maximized. However, both CCA and MVCCA are unsupervised and therefore do not guarantee a subspace that is optimal for class separation. sMVCCA is a supervised form of MVCCA where class labels are embedded as one of the variable sets. Additional details and formulations for CCA and MVCCA are provided in the appendix and the theoretical framework for sMVCCA is provided below. Table 2 provides a summary of notations used in this section.
Consider a multimodal dataset \({\bf{X}}\in \{{x}_{1},\ldots ,{x}_{k},\ldots ,{x}_{K}\}\) in \({{\mathbb{R}}}^{n\times M}\), where n is the number of subjects, K is the number of modalities and x k in \({{\mathbb{R}}}^{n\times {M}_{k}}\) refers to the feature matrix of modality k containing M k features. Additionally, X has a corresponding binary class label matrix Y in \({{\mathbb{R}}}^{n\times G}\), where G is the total number of classes. sMVCCA seeks to maximize correlation within the modalities in X and between X and Y as shown below
This can be expressed in a compact matrix form as follows:
where Y is a matrix in which class labels are encoded using Soft-1-of-Class strategy32.
Solving Equation 3 consists of two steps: (i) Ignoring the constraint in (4) leaves us with a quadratic programming problem, whose W* corresponds to eigenvectors of the n-largest eigenvalues of a generalized eigenvalue system: \({{\bf{C}}}_{{\bf{xy}}}{\bf{W}}=\lambda {{\bf{C}}}_{{{\bf{d}}}_{{\bf{xy}}}}{\bf{W}}\); (ii) Imposing constraint (4) upon obtaining the optimal eigenvectors W* by normalizing the corresponding section of each modality: \({{\bf{W}}}_{{\bf{j}}}^{\ast \ast }={{\bf{W}}}_{{\bf{j}}}^{\ast }{({{\bf{W}}}_{{\bf{j}}}^{\ast {\bf{T}}}{{\bf{C}}}_{{\bf{jj}}}{{\bf{W}}}_{{\bf{j}}}^{\ast })}^{-\frac{1}{2}},j=1,\ldots ,k\).
Cascaded Multi-view Canonical Correlation Analysis (CaMCCo)
As shown in Fig. 2, CaMCCo divides the classification task for a multiclass, multimodal dataset into a cascade of multiple, sequential binary classification tasks, for each of which the optimal fused representation is independently determined and provided as input to the classifier. For the multimodal dataset X in \({{\mathbb{R}}}^{n\times M}\), consider a label matrix Y in \({{\mathbb{R}}}^{n\times G}\). A subset modalities suitable for classifying class g from all input samples can be denoted as i where \(i\subseteq k\). Features from modalities in i are concatenated to generate \({{\bf{X}}}_{{\bf{i}}}^{^{\prime} }\) in \({{\mathbb{R}}}^{n\times p}\), where \(p={\sum }_{i}{M}_{i}\) and \(p\le M\). The i modalities are fused via sMVCCA to reduce the dimensionality from p to d, where \(d\ll p\), resulting in \({{\bf{X}}}_{{\bf{i}}}^{^{\prime\prime} }\). Subsequently, \({{\bf{X}}}_{{\bf{i}}}^{^{\prime\prime} }\) serves as the input to a classifier which predicts if each sample does or does not belong to class g, \({\hat{y}}_{g}=1\) and \({\hat{y}}_{g}=0\), respectively. The multimodal dataset consisting of only samples classified as \(\hat{y}=0\) subsequently serves as the input for the next level of cascade where the modality selection, data fusion and classification steps are repeated for another class in Y.
Therefore, designing the cascaded classifier for CaMCCo requires determination of (a) the sequence of classification tasks that provide the best overall classifier performance, as well as the respective (b) number and (c) type of modalities to combine at each level of the cascade. In this work, these parameters were determined experimentally on the training cohort as described in Section 3.5.
Experimental Design
Dataset Description
Data used in the preparation of this work were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (www.loni.ucla.edu/ADNI). The ADNI was launched in 2003 with the primary goal of testing whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). The initial goal of ADNI was to recruit 800 adults, ages 55 to 90, to participate in the research – approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years, and 200 people with early AD to be followed for 2 years (see www.adni-info.org for up-to-date information). The research protocol was approved by each local institutional review board and written informed consent. In addition to raw data, the ADNI database contains several post-processed and individually evaluated biomarkers.
In this work, we consider a subset of cases for which the following was available in the database (i) pre-computed features from T1w MRI and FDG PET, (ii) neurocognitive ADAS-cog score, (iii) complete record of CSF Proteomics, Plasma Proteomics, ApoE and (iv) clinical diagnosis at baseline. 149 ADNI participants who fulfilled the criteria were included, of which 52 were diagnosed with Alzheimer’s Disease (AD), 71 were diagnosed with mild cognitive impairment (MCI), and 26 were healthy controls (HC).
Table 3 provides the clinical and demographic details of the population considered in this study as per their diagnosis at baseline. The unique ADNI database provided RID of all patients considered in this study is provided in the Appendix.
Feature Description
Table 4 summarizes the number and types of features considered in this study for each modality. From imaging data, we consider volumetric features extracted from T1w MRI and measures of hippocampal glucose metabolism33, 34 from FDG PET. Considered molecular markers include proteomic measurements from cerebrospinal fluid (CSF), plasma from the biomarker consortium and geneotype ApoE data. We additionally included a neurophysiological test score as such tests serve as the primary means for diagnosis in the current clinical setting. Although the Mini-Mental State Examination (MMSE) is the most commonly performed clinical test, we avoid using MMSE scores as they were used to determine the “ground truth” labels on which we train and test CaMCCo. Therefore, we use an alternate test score, modified Alzheimer’s Disease Assessment Scale - Cognition (ADAS-Cog) which has been used to assess the effects of experimental treatments for AD in clinical trials35.
Classification Model
The dataset was split into training and a holdout validation set with each comprising 40% and 60% of the data, respectively. Classification and fusion parameters were determined on the training set using 10 iterations of 5-fold stratified cross validation, upon which the optimized classifier trained on the full training set was applied to the independent validation set. Naive Bayes classifier36 was used to evaluate the various fused and individual modality representations. Naive Bayes is a widely used, well-established probabilistic classifier that is known to perform well on small datasets.
Evaluation metrics
Performance measures used to evaluate each classification task include: accuracy (ACC), balanced accuracy (BACC)37, area under the receiver operating characteristic curve (AUC)38, sensitivity (SEN), specificity (SPE) and positive predictive value (PPV). The definitions and descriptions of each of these metrics are provided in Table 8 in the Appendix.
CaMCCO Model
Class groupings and modalities selected for fusion at each level of the cascaded classification design employed by CaMCCo (Fig. 1) was determined experimentally on the training set. One-vs-all (AD vs. all, MCI vs. all, HC vs. all) classifiers were constructed and evaluated independently for each considered modality. The task that most consistently resulted in the highest AUC across all modalities served as the first level of the cascade so as to reduce error propagation. Among AD, MCI and HC, the remaining classes were assigned to the second level of the cascade.
For every classification task within the cascade, each modality was ranked based on the AUC it achieved across iterations and cross validation folds within the training set. The n highest performing modalities were fused via sMVCCA, where n was varied from 2 to 6 (total number of considered modalities). The n modalities, which in combination, provided the highest training AUC were selected.
Comparative Strategies
CaMCCo represents a framework (\( {\mathcal H} \)) composed of multiple modules corresponding to modality selection (\({\mathscr{K}}\)), multimodal data fusion (\( {\mathcal F} \)), and multiclass classification (\({\mathscr{C}}\)). Accordingly, the comparative strategies against which we evaluate CaMCCo involve systematically replacing the method used for one or more of these modules with an alternative strategy. Table 5 lists the notation for each of these strategies and provides a short description.
Single Modality and Multimodality Approaches
Each modality was evaluated using a single modality framework (\({ {\mathcal H} }_{MRI}\), \({ {\mathcal H} }_{PET}\), \({ {\mathcal H} }_{CSF}\), \({ {\mathcal H} }_{PP}\), \({ {\mathcal H} }_{APOE}\), \({ {\mathcal H} }_{ADAS}\)) consisting of cascaded classification (\({{\mathscr{C}}}_{CAS}\)) to ensure fair comparison with CaMCCo. In addition, we compared classification performance of CaMCCo with that of a cascaded classification model where all modalities were fused at each level of the cascade (\({ {\mathcal H} }_{ALL}\)).
Principal Component Analysis for Data Fusion
Principal Component Analysis (PCA) is a dimensionality reduction method which projects input data onto an alternate subspace defined by orthogonal basis vectors which capture the direction of variance in the data. Consider a high dimensional, concatenated multimodal data matrix \({\bf{X}}=[{x}_{1},\ldots ,{x}_{k},\ldots {x}_{K}]\in {{\mathbb{R}}}^{n\times {M}_{1}+\ldots +{M}_{k}+\ldots +{M}_{K}}\) where K refers to the number of modalities, n refers to the number of subjects, and M k refers to the number of features in modality k.
Singular value decomposition is applied to mean centered data matrix, \(\bar{{\bf{X}}}\), which results in U, S, V. The columns of \({\bf{V}}\in {{\mathbb{R}}}^{({M}_{1}+\ldots +{M}_{k}+\ldots +{M}_{K})\times ({M}_{1}+\ldots +{M}_{k}+\ldots +{M}_{K})}\) are the principal components of \(\bar{{\bf{X}}}\) or the orthogonal basis vectors, ordered decreasingly by the amount of variance in the dataset explained by each component. \({\bf{U}}\in {{\mathbb{R}}}^{n\times {M}_{1}+\ldots +{M}_{k}+\ldots +{M}_{K}}\) contains the projections of \(\bar{{\bf{X}}}\) on the subspace defined by V. \({\bf{S}}\in {{\mathbb{R}}}^{({M}_{1}+\ldots +{M}_{k}+\ldots +{M}_{K})\times ({M}_{1}+\ldots +{M}_{k}+\ldots +{M}_{K})}\) is a diagonal matrix. To reduce data dimensionality, the top d principal components containing most of the variance in the data are retained, onto which the data is projected.
Multiclass Classification
For a classification task with G classes, One-vs-All (OVA) method constructs G classifiers, each tailored to separate one class from the rest. One Shot Classification (OSC) generates a single classifier designed to simultaneously distinguish between all the classes. The last comparative strategy involves the following binary classification tasks, AD vs. HC and MCI vs. HC.
Experiment 1: Single Modality and Multi-Modality Cascaded Classification
The objective of this experiment is to examine (i) classification performance achieved by combining multiple modalities as compared to any single modality for all classification tasks within the cascade design. In addition, the experiment seeks to determine if (ii) combining subsets of modalities tailored to optimize classification at each level of the cascade provides comparable and/or improved performance as compared to combining all the modalities for all tasks. Finally, it also evaluates (iii) the impact of the chosen fusion method on the findings for (i) and (ii).
To meet these objectives, we compare the data fusion (\( {\mathcal F} \)) and modality selection (\({\mathscr{K}}\)) modules in CaMCCo (\({ {\mathcal H} }_{CAMCCO}={{\mathscr{C}}}_{CAS}+{ {\mathcal F} }_{SMVCCA}+{{\mathscr{K}}}_{SEL}\)) with other fusion (\({ {\mathcal F} }_{PCA}\)), and modality selection (\({{\mathscr{K}}}_{ALL}\)) approaches, including the simple single modality (\({{\mathscr{K}}}_{MRI}\), \({{\mathscr{K}}}_{PET}\), \({{\mathscr{K}}}_{CSF}\), \({{\mathscr{K}}}_{PP}\), \({{\mathscr{K}}}_{APOE}\), \({{\mathscr{K}}}_{ADAS}\)) classification. For individual modality experiments, PCA was applied to the experiments where the number of features were larger than the number of samples to avoid curse of dimensionality. For fused and concatenated classifiers, the number of reduced dimensions was optimized on the training set. Therefore, we consider all the combinations of modalities and fusion methods listed below:
Experiment 2: Comparison of Multi-Class Classification Strategies for Fused Predictors
The objective of this experiment is to compare the cascaded classification method \({{\mathscr{C}}}_{CAS}\) used in CaMCCo (\({ {\mathcal H} }_{CAMCCO}={{\mathscr{C}}}_{CAS}+{ {\mathcal F} }_{SMVCCA}+{{\mathscr{K}}}_{SEL}\)) with other multiclass classification methods including OVA (\({{\mathscr{C}}}_{OVA}\)) and OSC (\({{\mathscr{C}}}_{OSC}\)). To ensure that only the classification module of the CaMCCo framework is evaluated, comparative classification strategies are combined with the same data fusion (\({ {\mathcal F} }_{SMVCCA}\)) and modality selection method (\({{\mathscr{K}}}_{SEL}\)) as CaMCCo. Therefore,\({ {\mathcal H} }_{OVA}={{\mathscr{C}}}_{OVA}+{ {\mathcal F} }_{SMVCCA}+{{\mathscr{K}}}_{SEL}\), and \({ {\mathcal H} }_{OSC}={{\mathscr{C}}}_{OSC}+{ {\mathcal F} }_{SMVCCA}+{{\mathscr{K}}}_{SEL}\). As with CaMCCo, the optimal set of modalities to combine for each classification task associated with OVA and OSC are determined experimentally from the training set.
Experiment 3: Evaluation of Fused Representation on Binary Classification Tasks
We perform binary classification (\({{\mathscr{C}}}_{BIN}\)) for the following two sets of classes, HC vs. AD and MCI vs. HC, in order to allow for direct comparison of the performance of fusion approach used in CaMCCo (\({ {\mathcal F} }_{SMVCCA}\) + \({{\mathscr{K}}}_{SEL}\)) with that reported in literature. As with CaMCCo, the optimal set of modalities to combine for each classification task are determined experimentally from the training set. In addition, we also report binary classification results achieved by individual modalities to examine the effect of fusion for these classification tasks and also to gain insight into the differences in classifier performance on account of the data cohort used in this study as compared to those in other studies.
Results and Discussion
Experiment 1: Single Modality and Multi-Modality Cascaded Classification
Figure 3 shows the performance of cascaded classifier when applied to (i) single modalities (\({ {\mathcal H} }_{MRI}\), \({ {\mathcal H} }_{PET}\), \({ {\mathcal H} }_{CSF}\), \({ {\mathcal H} }_{PP}\), \({ {\mathcal H} }_{APOE}\), \({ {\mathcal H} }_{ADAS}\)), (ii) fusion of all modalities (\({ {\mathcal H} }_{ALL}\), \({ {\mathcal H} }_{PCAL}\)) and (iii) fusion of selected modalities with multiple fusion methods (\({ {\mathcal H} }_{CAMCCO}\), \({ {\mathcal H} }_{PCA}\)) for prediction of HC, MCI and AD on the testing cohort. As shown in Fig. 1, ADAS-Cog, CSF and APOE were combined at the first cascade level (HC vs. All) and ADAS-Cog, and PET were combined at the second level (AD vs. MCI) in both \({ {\mathcal H} }_{CAMCCO}\) and \({ {\mathcal H} }_{PCA}\). For HC vs. all, \({ {\mathcal H} }_{CAMCCO}\) shows higher performance (AUC = 0.97) as compared to all individual modalities (max AUC = 0.93), \({ {\mathcal H} }_{PCA}\) (AUC = 0.94), \({ {\mathcal H} }_{PCAL}\) and \({ {\mathcal H} }_{ALL}\) (AUC = 0.52). Among the individual modalities, \({ {\mathcal H} }_{ADAS}\), \({ {\mathcal H} }_{CSF}\) and \({ {\mathcal H} }_{APOE}\) provided the top 3 classification AUCs, which was consistent with observations in the training set which led to these three modalities being selected for fusion in CaMCCo.
For AD vs. MCI, \({ {\mathcal H} }_{CAMCCO}\), \({ {\mathcal H} }_{PCA}\) and \({ {\mathcal H} }_{ADAS}\) showed similar performances (AUC = 0.89). This may, in part, be on account of the lack of orthogonality in the features being fused. A correlation test between the ADAS and PET features showed correlation coefficients between −0.49 and −0.51 with p-value < 0.01. In fact, the modality selection strategy employed in this work is limited in that it does not account for relationships between modalities to identify those that optimize the performance when fused. Instead, the selection of modalities are simplified and are based on their individual performances. However, it is interesting to note that despite the significantly poorer performance of \({ {\mathcal H} }_{PET}\) as compared to \({ {\mathcal H} }_{ADAS}\), combining PET with ADAS-Cog does not degrade the performance. We note that, similar to HC vs. All, \({ {\mathcal H} }_{CAMCCO}\) significantly outperforms \({ {\mathcal H} }_{ALL}\).
Experiment 2: Comparison of Multi-Class Classification Strategies for Fused Predictors
Table 6 shows the performance of \({ {\mathcal H} }_{CAMCCO}\), \({ {\mathcal H} }_{OVA}\) and \({ {\mathcal H} }_{OSC}\) for prediction of HC, MCI and AD. Across all 3 classes, it is evident that \({ {\mathcal H} }_{OVA}\) and \({ {\mathcal H} }_{CAMCCO}\) outperform \({ {\mathcal H} }_{OSC}\). \({ {\mathcal H} }_{OVA}\) and \({ {\mathcal H} }_{CAMCCO}\) show comparable AUCs for AD classification, although \({ {\mathcal H} }_{OVA}\) shows incrementally higher accuracy, sensitivity and specificity as compared to \({ {\mathcal H} }_{CAMCCO}\). For MCI classification however, \({ {\mathcal H} }_{CAMCCO}\) significantly outperforms \({ {\mathcal H} }_{OVA}\) in terms of all metrics (OVA AUC = 0.78 vs. CaMCCo AUC = 0.88). This is on account of the lower classification performance of MCI vs. all which is a challenging task provided the heterogeneity of the ‘all’ category which consists of both AD and HC patients. Therefore, CaMCCo provides the most optimal performance overall, across all 3 classes.
Experiment 3: Evaluation of Fused Representation on Binary Classification Tasks
Table 7 shows \({ {\mathcal H} }_{BIN}\) results obtained by combining select few modalities (\({{\mathscr{K}}}_{SEL}\)) via sMVCCA (\({ {\mathcal F} }_{SMVCCA}\)) for the following binary classification tasks: (i) AD vs. HC and (ii) MCI vs. HC. On the training set, the fusion of ADAS-Cog and CSF provided the best classification AUC for AD vs. HC whereas the fusion of ADAS-Cog, CSF and PET provided the best classification for MCI vs. HC. Thus, \({ {\mathcal H} }_{BIN}\) for the two classification tasks fused the respective, aforementioned modalities for the test set. For the former classification task, the performance of \({ {\mathcal H} }_{BIN}\) was similar to that of the best performing individual modality, ADAS-Cog, which already provided near perfect AUC leaving little scope for improvement. According to other evaluation metrics, ADAS-Cog outperforms the fused representation. For the more challenging MCI vs. HC classification task however, \({ {\mathcal H} }_{BIN}\) improves classifier performance slightly in terms of AUC (0.92 vs. 0.93) but more significantly in terms of BACC (0.77 vs. 0.82) and SPEC (0.65 vs. 0.71). In comparison to most previous work, our individual modality and fused modality results appear to be slightly higher possibly on account of the features that were considered in this work, all of which were quality controlled and independently proven to provide good performance previously. In addition, this work considers a neurocognitive score (ADAS-Cog), a measure that is mostly either used as a response variable or unconsidered in many fusion studies. The ADAS score appears to be strongly predictive of all classification tasks, possibly on account of a strong correlation with the MMSE scores, which were used to derive the ground truth class labels. Therefore, most gains in classification accuracy appears to be only slightly incremental. A correlation test between ADAS scores and MMSE scores across 118 patients, who had the latter data available, showed that the two were indeed highly correlated with a coefficient of −0.65 and p-value < 0.01.
Conclusion
In this work, we present a joint cascaded classification and radio-omics data fusion framework, called Cascaded Multiview Canonical Correlation (CaMCCo), for early diagnosis of Alzheimer’s disease. CaMCCo employs a unique strategy as compared to most previous approaches in that it accounts for multiclass classification while attempting to optimize classification accuracy by fusing a select subset of modalities for prediction of each class. As a framework, CaMCCo is comprised of three modules: (i) data fusion, (ii) modality selection and (iii) multiclass classification. Experiments were designed to investigate the choice of methods used for each CaMCCo module independently. In the first experiment, for instance, classification method was held constant while the data fusion and modality selection modules were varied and compared with that of CaMCCo. In the second experiment, the modality selection and data fusion methods were held constant and the cascaded classifier in CaMCCo was compared against other multiclass classification methods. Experimental findings on the ADNI dataset, comprising imaging, proteomics, genomics and neurophysiological data, consistently indicated that fusion of select multi-scale data channels, as in CaMCCo, outperforms fusion of all available modalities. In addition, the results showed that cascaded classification used in CaMCCo is better suited than other multi-class classification methods for MCI prediction. Finally, CaMCCo was compared against individual modalities for the two most commonly investigated binary classification tasks in most related studies, AD vs. HC and MCI vs. HC. While AD vs. HC was a simpler task well resolved by a single modality in our study, MCI vs. HC was a more challenging task where the application of CaMCCo appeared to improve classification, most significantly in terms of specificity. CaMCCo appears to be better able to distinguish between MCI and HC as compared to most previous studies, some of which are listed in Table 5.
However, the work presented in this paper is limited mainly by the method with which the modalities to be combined at each level of the cascade is determined. We only combine the modalities that independently provide the best accuracies on the training set, which may not be complementary. Nonetheless, we found that considering a subset of modalities provides improved performance over fusing all modalities. These findings indicate that incorporation of a more advanced modality selection method and additionally a feature selection method into the framework may provide further improvement in performance. Another limitation of the proposed strategy is the propagation of error from one level of the cascade to the next. To minimize this error, we therefore begin the cascade with the one-vs-all classification providing the least error. Despite these limitations, current findings indicate that the presented framework provides a promising platform for fusion of multiscale, multimodal data for early diagnosis of Alzheimer’s Disease.
References
McKhann, G. M. et al. The diagnosis of dementia due to alzheimer’s disease: Recommendations from the national institute on aging-alzheimer’s association workgroups on diagnostic guidelines for alzheimer’s disease. Alzheimer’s & Dementia 7, 263–269 (2011).
Association, A. et al. Alzheimer’s disease facts and figures. Alzheimer’s & dementia: the journal of the Alzheimer’s Association 8, 131 (2012).
Brookmeyer, R., Gray, S. & Kawas, C. Projections of alzheimer’s disease in the united states and the public health impact of delaying disease onset. American journal of public health 88, 1337–1342 (1998).
Knopman, D. et al. Practice parameter: Diagnosis of dementia (an evidence-based review) report of the quality standards subcommittee of the american academy of neurology. Neurology 56, 1143–1153 (2001).
Carrillo, M. C. et al. Revisiting the framework of the national institute on aging-alzheimer’s association diagnostic criteria. Alzheimer’s & Dementia 9, 594–601 (2013).
Mattsson, N. et al. Csf biomarkers and incipient alzheimer disease in patients with mild cognitive impairment. Jama 302, 385–393 (2009).
Hansson, O. et al. Association between csf biomarkers and incipient alzheimer’s disease in patients with mild cognitive impairment: a follow-up study. The Lancet Neurology 5, 228–234 (2006).
Wallin, A., Blennow, K., Andreasen, N. & Minthon, L. Csf biomarkers for alzheimer’s disease: levels of beta-amyloid, tau, phosphorylated tau relate to clinical symptoms and survival. Dementia and geriatric cognitive disorders 21, 131–138 (2005).
Saunders, A. et al. Specificity, sensitivity, and predictive value of apolipoprotein-e genotyping for sporadic alzheimer’s disease. The Lancet 348, 90–93 (1996).
Deweer, B. et al. Memory disorders in probable alzheimer’s disease: the role of hippocampal atrophy as shown with mri. Journal of Neurology, Neurosurgery & Psychiatry 58, 590–597 (1995).
Coleman, R. E. Positron emission tomography diagnosis of alzheimer’s disease. PET Clinics 2, 25–34 (2007).
Madabhushi, A., Agner, S., Basavanhally, A., Doyle, S. & Lee, G. Computer-aided prognosis: predicting patient and disease outcome via quantitative fusion of multi-scale, multi-modal data. CMIG 35, 506–14 (2011).
Madabhushi, A. et al. Integrated diagnostics: a conceptual framework with examples. Clinical chemistry and laboratory medicine 48, 989–998 (2010).
Lee, G. et al. A knowledge representation framework for integration, classification of multi-scale imaging and non-imaging data: Preliminary results in predicting prostate cancer recurrence by fusing mass spectrometry and histology. In Biomedical Imaging: From Nano to Macro, 2009. ISBI’09. IEEE International Symposium on, 77–80 (IEEE, 2009).
Tiwari, P., Viswanath, S., Lee, G. & Madabhushi, A. Multi-modal data fusion schemes for integrated classification of imaging and non-imaging biomedical data. In Biomedical Imaging: From Nano to Macro, 2011 IEEE International Symposium on, 165–168 (IEEE, 2011).
Kern, S. E. Why your new cancer biomarker may never work: recurrent patterns and remarkable diversity in biomarker failures. Cancer research 72, 6097–6101 (2012).
Rohlfing, T. & Maurer, C. R. Multi-classifier framework for atlas-based image segmentation. Pattern Recognition Letters 26, 2070–2079 (2005).
Da, X. et al. Integration and relative value of biomarkers for prediction of mci to ad progression: Spatial patterns of brain atrophy, cognitive scores, apoe genotype and csf biomarkers. NeuroImage: Clinical 4, 164–173 (2014).
Davatzikos, C., Bhatt, P., Shaw, L. M., Batmanghelich, K. N. & Trojanowski, J. Q. Prediction of mci to ad conversion, via mri, csf biomarkers, and pattern classification. Neurobiology of aging 32, 2322–e19 (2011).
Zhang, D. et al. Multimodal classification of alzheimer’s disease and mild cognitive impairment. Neuroimage 55, 856–867 (2011).
Hinrichs, C. et al. Predictive markers for ad in a multi-modality framework: an analysis of mci progression in the adni population. Neuroimage 55, 574–589 (2011).
Gray, K. R. et al. Random forest-based similarity measures for multi-modal classification of alzheimer’s disease. NeuroImage 65, 167–175 (2013).
Suk, H.-I., Lee, S.-W., Shen, D. & Initiative, A. D. N. et al. Hierarchical feature representation and multimodal fusion with deep learning for ad/mci diagnosis. NeuroImage 101, 569–582 (2014).
Liu, S. et al. Multimodal neuroimaging feature learning for multiclass diagnosis of alzheimer’s disease. IEEE Transactions on Biomedical Engineering 62, 1132–1140 (2015).
Lewis, D. P., Jebara, T. & Noble, W. S. Support vector machine learning from heterogeneous data: an empirical analysis using protein sequence and structure. Bioinformatics 22, 2753–2760 (2006).
Golugula, A. et al. Supervised regularized canonical correlation analysis: integrating histologic and proteomic measurements for predicting biochemical recurrence following prostate surgery. BMCB 12, 483 (2011).
Singanamalli, A. et al. Supervised multi-view canonical correlation analysis: Fused multimodal prediction of disease prognosis. In SPIE Medical Imaging, 903805–903805 (2014).
Lee, G. et al. Supervised multi-view canonical correlation analysis (smvcca): integrating histologic and proteomic features for predicting recurrent prostate cancer. IEEE transactions on medical imaging 34, 284–297 (2015).
Richard, E., Schmand, B. A., Eikelenboom, P. & Van Gool, W. A. Mri and cerebrospinal fluid biomarkers for predicting progression to alzheimer’s disease in patients with mild cognitive impairment: a diagnostic accuracy study. BMJ open 3, e002541 (2013).
Kettenring, J. R. Canonical analysis of several sets of variables. Biometrika 58, 433–451 (1971).
Hotelling, H. Relations between two sets of variates. Biometrika 28, 321–377 (1936).
Sun, T. & Chen, S. Class label versus sample label-based cca. Applied Mathematics and computation 185, 272–283 (2007).
Mosconi, L. et al. Reduced hippocampal metabolism in mci and ad automated fdg-pet image analysis. Neurology 64, 1860–1867 (2005).
Li, Y. et al. Regional analysis of fdg and pib-pet images in normal aging, mild cognitive impairment, and alzheimer’s disease. European journal of nuclear medicine and molecular imaging 35, 2169–2181 (2008).
Petersen, R. C. et al. Vitamin e and donepezil for the treatment of mild cognitive impairment. New England Journal of Medicine 352, 2379–2388 (2005).
Friedman, J., Hastie, T. & Tibshirani, R. The elements of statistical learning, vol. 1 (Springer series in statistics Springer, Berlin, 2001).
Brodersen, K. H., Ong, C. S., Stephan, K. E. & Buhmann, J. M. The balanced accuracy and its posterior distribution. In Pattern recognition (ICPR), 2010 20th international conference on, 3121–3124 (IEEE, 2010).
Fawcett, T. An introduction to roc analysis. Pattern recognition letters 27, 861–874 (2006).
Westman, E., Muehlboeck, J.-S. & Simmons, A. Combining mri and csf measures for classification of alzheimer’s disease and prediction of mild cognitive impairment conversion. Neuroimage 62, 229–238 (2012).
Zhu, X., Suk, H.-I. & Shen, D. Sparse discriminative feature selection for multi-class alzheimer?s disease classification. In Machine Learning in Medical Imaging, 157–164 (Springer, 2014).
Mohs, R. C. et al. Development of cognitive instruments for use in clinical trials of antidementia drugs: additions to the alzheimer’s disease assessment scale that broaden its scope. Alzheimer Disease & Associated Disorders 11, 13–21 (1997).
Binukumar, B. & Pant, H. C. Candidate Bio-Markers of Alzheimer’s Disease (INTECH Open Access Publisher, 2013).
Ray, S. et al. Classification and prediction of clinical alzheimer’s diagnosis based on plasma signaling proteins. Nature medicine 13, 1359–1362 (2007).
Acknowledgements
Research reported in this publication was supported by the National Cancer Institute of the National Institutes of Health under award numbers 1U24CA199374-01, R01CA202752-01A1, R01CA208236-01A1, R21CA179327-01, R21CA195152-01, the National Institute of Diabetes and Digestive and Kidney Diseases under award number R01DK098503-02, National Center for Research Resources under award number 1 C06 RR12463-01, the DOD Prostate Cancer Synergistic Idea Development Award (PC120857); the DOD Lung Cancer Idea Development New Investigator Award (LC130463), the DOD Prostate Cancer Idea Development Award, the DOD Peer Reviewed Cancer Research Program W81XWH-16-1-0329; the Case Comprehensive Cancer Center Pilot Grant VelaSano Grant from the Cleveland Clinic the Wallace H. Coulter Foundation Program in the Department of Biomedical Engineering at Case Western Reserve University. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen Idec Inc.; Bristol-Myers Squibb Company; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare;; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Medpace, Inc.; Merck & Co., Inc.; Meso Scale Diagnostics,LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Synarc Inc.; and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
Author information
Authors and Affiliations
Author notes
A comprehensive list of consortium members appears at the end of the paper
Consortia
Contributions
A.S. designed the study, conducted the experiments and prepared the manuscript. H.W. provided expert advice and contributed to methods development. A.M. provided supervision. All authors reviewed the manuscript. Data used in preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (www.loni.ucla.edu/ADNI). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf.
Corresponding authors
Ethics declarations
Competing Interests
Conflict of interest disclosures for Anant Madabhushi: Inspirata-Stock Options/Consultant/Scientific Advisory Board Member, Elucid Bioimaging Inc.-Stock Options, Siemens, GE-NIH Academic Industrial Partnership.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Singanamalli, A., Wang, H., Madabhushi, A. et al. Cascaded Multi-view Canonical Correlation (CaMCCo) for Early Diagnosis of Alzheimer’s Disease via Fusion of Clinical, Imaging and Omic Features. Sci Rep 7, 8137 (2017). https://doi.org/10.1038/s41598-017-03925-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-03925-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.