Abstract
We present a fully digital procedure of designing reflective coding metasurfaces to shape reflected electromagnetic waves. The design procedure is completely automatic, controlled by a personal computer. In details, the macro coding units of metasurface are automatically divided into several types (e.g. two types for 1-bit coding, four types for 2-bit coding, etc.), and each type of the macro coding units is formed by discretely random arrangement of micro coding units. By combining an optimization algorithm and commercial electromagnetic software, the digital patterns of the macro coding units are optimized to possess constant phase difference for the reflected waves. The apertures of the designed reflective metasurfaces are formed by arranging the macro coding units with certain coding sequence. To experimentally verify the performance, a coding metasurface is fabricated by automatically designing two digital 1-bit unit cells, which are arranged in array to constitute a periodic coding metasurface to generate the required four-beam radiations with specific directions. Two complicated functional metasurfaces with circularly- and elliptically-shaped radiation beams are realized by automatically designing 4-bit macro coding units, showing excellent performance of the automatic designs by software. The proposed method provides a smart tool to realize various functional devices and systems automatically.
Similar content being viewed by others
Introduction
In modern information science and technology, the printed microstrip reflectarray has been widely used as a kind of flat reflection-type antennas, which is generally composed of an array of radiating elements on a grounded substrate1. A lot efforts have been devoted to the researches of the printed microstrip reflectarray, which features the advantages of versatile radiation performances, compact structure, simple profile, and low cost as high-gain antennas2. Owning to such desirable features of traditional parabolic reflectors and planar phased arrays, it is more convenient for the reflectarray to produce the directive and shaped beams through the reflection phases of array elements3. In virtue of the diversity of element structures and relevant parameters, there are different reflection phases when the feeding source irradiates the microstrip patch elements4,5,6. Every element is independently controllable for the compensated phase of the phase delay caused by the path difference. However, one serious weakness of the printed microstrip reflectarray is the limited bandwidth7. Many techniques have been proposed to expand the working bandwidth, including using multilayer structure, true-time delay, subwavelength patch elements and dual-frequency phase synthesis method8,9,10,11,12.
On the other hand, various kinds of metasurfaces have been presented in recent years to control the radiation and scattered electromagnetic beams by designing gradient phases profiles on the metasurface, for example the anomalous reflection and refraction governed by the generalized Snell’s law13,14,15,16, polarization-state conversions17,18,19, conversions from spatial modes to surface modes20, optical-vortex generations21,22,23, and photonic spin hall effect24,25,26, etc. More recently, novel concepts of coding metasurface, digital metasurface, programmable metasurface, and reconfigurable reflectarray have been proposed27,28,29,30,31,32, which provide more freedoms and capabilities to control the electromagnetic waves and lights. However, most of the designs of reflectarrays and metasurfaces require many manual works (i.e. numerical simulations) to achieve the desired reflection phases of array elements.
To solve this problem, we propose in this work a software-based automatic-approach to provide an efficient way for automatic designs of unit cells using the optimization algorithm and commercial electromagnetic software. The particle swarm optimization (PSO) is an evolutionary computation model based on the swarm intelligence, which has been utilized in the function optimization, artificial neural network training, fuzzy control and other fields33,34,35,36. To solve the discrete combinatorial optimization problem, Kennedy and Eberhart have put forward the binary PSO (BPSO), whose particles are composed of binary encoding37. Because both discrete and continuous problems can be expressed by binary encoding, BPSO has much more practical application values38, 39. BPSO can be performed easily with profound intelligent background, and some improved algorithms have been developed in the scientific research and engineering applications40,41,42.
In this paper, we present software-automatically-designed unit cells based on the combination of discretely random square lattice, BPSO optimization, and electromagnetic computing software. We propose a software-based automatic-approach for the discretely random arrangement of micro coding units with the four-fold symmetry. The pattern of the micro coding units consists of many square metal sub-blocks, and different combinations of such sub-blocks will attach different phase compensations to the reflected waves. To get the desirable phase performance, we build up a bridge between the BPSO optimization algorithm and commercial software, CST Microwave Studio, to achieve the optimal arrangement of the square metal sub-blocks. On the basis of this method, we can obtain macro coding units of 1-bit coding elements with the phase difference of 180°, 2-bit coding elements with the phase difference of 90°, and so on, automatically over a broad operating frequency band. To verify the proposed method experimentally, we realize four-beam generations using the 1-bit coding elements, and circular/elliptical beam radiations using the automatically designed 4-bit coding elements with the constant phase difference of 22.5°. The numerical and experimental results are presented to confirm the good performance of the software-automatically-designed unit cells. The proposed method enables the automatic design of coding unit cells and provides us a smart tool for realizing multi-functional metasurface devices and systems.
Results
Micro macro coding units
In order to realize the automatic designs of metasurface elements, we propose a software-based automatic-approach for the discretely random arrangement of micro coding units which is divided into 16 × 16 square sub-blocks with the four-fold symmetry imposed on the design, as illustrated in Fig. 1. Hence we just need to optimize one quarter of the unit cell in the automatic design. The 16 × 16 square sub-blocks are either covered with the metal thin film or not, in which the sub-blocks with metal are shown by yellow color, representing with ‘1’ in the BPSO particles, whereas the sub-blocks without metal are shown by white color, representing with ‘0’ in the BPSO particles, as demonstrated in Fig. 1(a). The parameters l 1 = 10 mm and l 2 = 8 mm are respectively chosen to describe the lengths of the square unit cell and the pattern, and hence the length of the sub-block is l = 0.5 mm. There is an obvious space between adjacent unit cells to decrease mutual coupling. The metallic patterns are printed on a commercial dielectric substrate, F4B, with the relative permittivity of 2.65 (1 + 0.003i) and thickness of t 1 = 1 mm. The other side of the dielectric layer is the grounded substrate with annealed copper (electric conductivity σ = 5.8e + 007 S/m), and the thickness of the metallic layer is t = 0.018 mm, as depicted in Fig. 1(b).
Different compositions of ‘0’ and ‘1’ sub-blocks make it possible to realize the required amplitude and phase responses of unit cell. However, the manual sorting and designing of ‘0’ and ‘1’ sub-blocks is time-consuming, hard sledding, and has low efficiency owing to too many sub-blocks and too many arrangement possibilities. Here, we propose a software-based automatic-approach for the unit cell by optimizing the compositions of ‘0’ and ‘1’ sub-blocks using commercial software, CST Microwave Studio (MWS). To make automatic connection between the numerical simulations of unit cells and optimization algorithm, we firstly set up a bridge between the CST Microwave Studio and Matlab, the commercial mathematical software, in which CST MWS can call Matlab, and also be called by Matlab. When Matlab calls CST MWS, the CST MWS is the service system and Matlab is the management system. Because the two-dimensional array of ‘0’ and ‘1’ in Matlab has the capacity to tune the pattern of the unit cell, we can exploit MATLAB to create the ‘0’ and ‘1’ pattern and update the mode for CST MWS.
Here, the BPSO algorithm is utilized to achieve the optimal arrangement of the sub-blocks for our targets. In the PSO algorithm, the potential solution is regarded as a particle. In this BPSO algorithm, every particle is an n-dimensional vector, and every element of the vector is described by 0 or 1, for corresponding to a pattern of the unit cell. The speed of the particle indicates the probability of position change of the particle, which can be calculated analytically as
where rand 1 and rand 2 are the random numbers between 0 and 1 in Matlab, c 1 and c 2 are the acceleration constants, w is the inertia coefficient, \({{\rm{pbset}}}_{ij}^{k}\) is the individual optimal position, and \({{\rm{gbset}}}_{ij}^{k}\) is the global optimal position. In this design, x donates whether the sub-block is metal or not. In virtue of the expression of probability, the value of the speed should be confined to the range of 0 and 1. The Sigmoid function is usually used for the mapping whose formula is
Therefore, the particles are assigned through
The targets to be optimized are then evaluated by the function fitness(x) looking for the best parameters.
Figure 2 depicts the automatic-design flow of the micro coding unit cell, in which we do no need any manual interventions, except setting the initial conditions and pressing the start button at the beginning. In the CST module, the unit cell mode without pattern should be built before running the algorithm. The initial population is a set of two-dimensional arrays just containing 0 and 1, which are randomly generated by Matlab. Inputting the pattern homologous array to the unit cell mode, we can acquire the phase and amplitude of every unit cell for evaluating the fitness to the required values. Then the PSO module updates the particle speed and the population location in each step of iterations, and sends the updated pattern to the execute simulation calculation by CST. At last, through multiple iterations and evaluating the fitness, it is convenient to get the optimal pattern automatically for the desired target.
Because of the four-fold symmetry imposed on the design, the unit cell is not sensitive to the polarization direction for the normally incident waves. That is to say, there are the same responses for the transverse-electric (TE) and transverse-magnetic (TM) polarized waves, and hence we choose the TE polarized wave in all designs and simulations. As the first example, to obtain the broadband 1-bit micro coding units, the optimization target is set to the bandwidth for two unit cells with the phase difference of 180°. In order to simplify the optimization procedure, every particle is shown as a row vector containing 512 numbers of 0 or 1. The first half of the row vector is relative to the pattern of the first lattice unit cell, and the rest depicts the second lattice unit cell. The fitness function used for this optimization is
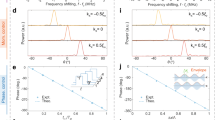
representing the bandwidth of the phase difference between 170° and 190° within the X band. An initial population of 30 particles is evolved for a maximum of 100 iterations. As geometrically illustrated in Figs. 3(a) and (b), we finally get the two optimized 1-bit micro coding units. From the reflection phases and amplitudes shown in Figs. 3(c) and (d), it is expedient to observe that the phase difference of the two unit cells satisfies the criterion aforementioned in the frequency band from 9.5 GHz to 10.3 GHz, while their reflection amplitudes are very close to 1.
Models, reflection phases and amplitudes of the 1-bit coding unit cells. (a) The geometry of the first coding unit cell. (b) The geometry of the second coding unit cell. (c) The reflection phases of the 1-bit coding unit cells and their phase difference. (d) The reflection amplitudes of the 1-bit coding unit cells.
Owing to the maneuverability of the automatic optimization method, we design broadband 2-bit coding unit cells, which consist of four coding unit cells with phase difference of 90°. The procedure of the automatic-design is running with three steps, each invoking three fitness functions. Firstly, Eq. (4) is employed to provide a pair of unit cells with 180° out of reflection phases, as shown geometrically in Figs. 4(b) and (d). The corresponding reflection phases and amplitudes of the two unit cells are donated as blue and red lines in Figs. 4(e) and (f), respectively. Then based on one of the two unit cells, the second and third fitness functions are added to search for the unit cells whose reflection phases differ from the basic unit cells by 90° and 270° phases. Two fitness functions are depicted as
and
Models, reflection phases and amplitudes of the 2-bit coding unit cells. (a) The geometry of the first coding unit cell. (b) The geometry of the second coding unit cell. (c) The geometry of the third coding unit cell. (d) The geometry of the fourth coding unit cell. (e) The reflection phases of the 2-bit coding unit cells. (f) The reflection amplitudes of the 2-bit coding unit cells.
In the second and third steps, every particle just needs 256 numbers for one pattern because the basic unit cell is ready. A population size of 60 and the maximum iterations of 100 are predefined. Figures 4(a) and (c) represent the remaining two unit cells of the 2-bit coding units, and their reflection phases and amplitudes are respectively presented by the black and green lines in Figs. 4(e) and (f). We note a frequency band from 10.6 to 11.1 GHz, where the reflection phases of these unit cells meet the requirement of 2-bit coding elements with almost zero boil-off.
Experiments and measured results
Based on the 1-bit coding unit cells, we design and fabricate a coding metasurface with periodic coding sequence 0101…/1010… for checking the performance of the automatic design of the macro coding unit cells, in which 4 × 4 arrays of 1-bit coding elements (supper lattices) constitute the digital codes ‘0’ and ‘1’. The coding metasurface contains 6 × 6 supper lattices under the periodic arrangement of 0101…/1010…, as shown in Fig. 5(a). The three-dimensional full- wave simulation results of the coding metasurface are illustrated in Fig. 5(b) at 10.2 GHz in the working frequency band, and we can observe four main beams obviously and intuitively. The working frequency band of the simulated results ranges from 9.6 to 10.4 GHz, and the small frequency offset with the designed unit cells mentioned above is mainly caused by the coupling between different unit cells. Figure 5(c) depicts the physically testing environment in the microwave chamber where the receiving horn antenna is connected to a vector network analyzer (Agilent N5230C) for showing the far-field radiation patterns. Because the macro coding unit cells are designed with four-fold symmetry, the coding metasurface is insensitive to the polarization direction of the normally incident waves. In order to view the testing results clearly, the sample is placed on a square foam with the angle of 45°. From the two-dimensional normalized radiation patterns at azimuth phi = 45°/225° in Figs. 5(d) and (e), we apparently observe two main beams and lower side lobes at 10.2 GHz for simulated results and 10.7 GHz for measured results, respectively. We can also notice the discrepancy and frequency offset between measured and simulated results. The reason for the gaps may be caused by the machining tolerance in fabrication and the influence of the testing environment such as the misalignment of the center of horns and testing sample.
Simulated and measured scattering patterns for coding metasurface with 1-bit macro coding units. (a) Geometry of the coding metasurface with periodic coding sequence 0101…/1010…. (b) 3D full-wave simulation results of the coding metasurface. (c) The experimental setup for the far-field measurement in the microwave chamber. The (d) simulated, and (e) measured results of the 2D normalized radiation patterns at azimuth phi = 45°/225°.
4-bit macro coding units
Since the random square lattice structures and their software-based automatic-approach have the characteristics of simplicity, convenience, and versatility, it is flexible to cope them with various complexities. There is a concise and fast procedure to create a series of multifarious reflection phases at specific frequencies. We choose 4-bit unit cells to cover the phase range of 360° at 10 GHz, so that the phase difference between two adjacent unit cells is assigned to 22.5° for uniformity. In order to facilitate the operation, the ideal reflection phases of 4-bit unit cells are programmed as
Based on the ideal values, the fitness function is set to
Here, every particle is composed of 256 numbers for one pattern, and the initial population has 80 particles. After the maximum iterations scheduled for 100, the final optimized patterns of the 4-bit macro coding unit cells are described in Figs. 6(a–p), in which the inserted digits indicate the actual reflection phases, possessing 180.316°, 157.633°, 134.762°, 112.582°, 89.612°, 67.578°, 45.129°, 23.052°, 0.105°, −22.560°, −45.100°, −67.780o, −89.786o, −112.640o, −134.875o and −157.532°. Compared with the ideal reflection phases, the maximum deviation of the automatic designed values is less than 0.6°.
To verify the practicability of the automatic designs, we use such 4-bit macro coding units to fabricate two complicated functional metasurfaces, whose radiation beams are shaped as a circle and an ellipse, respectively. There are a variety of radiation effects by adjusting the arrangements of the macro unit cells. In order to radiate the corresponding shapes of beams, the required compensation phase for every unit cell is calculated as
where k 0 is the free space wavenumber, θ is the pitch angle, f(x, y) is the function of the desired radiation beam (circle or ellipse in this design), and (x, y) is the coordinate of the macro unit. For the convenience of computing, the substrate center is selected as the origin of the coordinate system. Thus we just need to calculate the compensation phase of a quarter of the metasurfaces because of the symmetry of the circular and elliptical beams. Benefiting from the automatic and software design by Matlab calling CST MWS, it is easy to create various metasurface such as quasi-circular and quasi-elliptic metasurface we choose. As shown in Figs. 7(a) and 8(a), the radius of the quasi-circular metasurface is 240 mm, and two semi-axis of the quasi-elliptic metasurface are respectively 240 mm, 120 mm. For the sake of the circular and elliptical beams, the function f(x, y) is respectively chosen as
Simulated 3D and 2D scattering patterns for the quasi-circular metasurface with the circularly shaped radiation beam. (a) Geometry of quasi-circular metasurface. (b) The 3D full-wave simulation result of the metasurface at 10 GHz. (c) The simulated 2D scattering far-field pattern at 10 GHz. (d) The simulated 2D normalized radiation pattern in the Cartesian coordinate at 10 GHz.
Simulated 3D and 2D scattering patterns for the quasi-elliptic metasurface with the elliptically shaped radiation beam. (a) Geometry of quasi-elliptic metasurface with the elliptically shaped radiation beam; (b) The 3D full-wave simulation result of the metasurface at 10 GHz; (c) The simulated 2D scattering far-field pattern at 10 GHz; (d) The simulated 2D normalized radiation pattern in the Cartesian coordinate at 10 GHz.
Substituting Eqs. (10) and (11) into (9), respectively, we can calculate the compensation phase distributions of the circle metasurfaces with θ = 36° and ellipse metasurface with θ = 40° at 10 GHz. If the compensation phase is in the range between P(i)−11.25° and P(i) + 11.25°, the macro unit cell i should be placed at that position. Thus the arrangements of the two complicated functional metasurfaces are illustrated in Figs. 7(a) and 8(a), respectively, radiating the circularly and elliptically shaped beams. From the 3D full- wave simulation results in Figs. 7(b) and 8(b), it is intuitive to see a circular beam and an elliptical beam above the substrate at 10 GHz. Imperfect cone-shaped beams are mainly due to the coupling among macro unit cells and the discretization of the phase and location. Figures 7(c) and 8(c) depict the simulated 2D scattering far-field pattern, showing complete circle and ellipse beams. As shown the 2D normalized radiation pattern of quasi-circular metasurface in the Cartesian coordinate in Fig. 7(d) at azimuth phi = 70°/250°, we can observe that the radiation direction of main lobe is 36° in any azimuth angle. Similarly, from Fig. 8(d) for the 2D normalized radiation patterns of quasi-elliptic metasurface, the radiation direction of main lobe of major axis is 20° at azimuth phi = 0°/180°, and the radiation direction of main lobe of minor axis is 40° at azimuth phi = 90°/270°. Thus, both the quasi-circular metasurface with radiating the circularly shaped beam and the quasi-elliptic metasurface with radiating the elliptically shaped beam have excellent agreements to the designed values.
Conclusion
Taking advantages of the novel optimization algorithm BPSO and the commercial software CST MWS, we can automatically obtain the satisfactory patterns of the random square lattice units (macro coding unit cells), which are composed of many square metal sub-blocks (micro coding unit cells) through different 2D arrangements. The software-based automatic-approach can achieve a maximum bandwidth for two macro coding units with phase difference of 180° and four macro coding units with phase difference of 90°, etc. In order to examine the performance of the software-based automatic-approach, we simulated and measured a coding metasurface with 0101…/1010… periodic coding sequence using the 1-bit macro coding elements. The numerical and experimental results demonstrated excellent performance of the 1-bit coding elements in a broad bandwidth. The software-based automatic-approach can also be used to search 4-bit macro coding units with sixteen fixed phases. We employ the 4-bit macro coding units to design two complicated functional metasurfaces, respectively, for radiating circularly and elliptically shaped beams. The full-wave simulated results are in excellent agreements with the design target. The proposed software-based automatic-approach for provides the versatility of coding units, and the novel optimization algorithm helps automatic designs of coding metasurfaces.
Methods
A bridge is built up between the BPSO optimization algorithm and commercial software, CST MWS, for numerical simulation to achieve the optimal arrangement of the square metal sub-blocks. Figure 2 vividly describe the detailed process of the connection between Matlab (BPSO) and CST MWS. The BPSO optimization algorithm run in Matlab which generate initial population and update the speed and the location of particles in each step of iterations through judging the termination condition. Then, Matlab call CST MWS, and input the particle for updating the pattern and mode of unit cell in CST MWS. CST MWS simulates the phase and amplitude of each unit cell and output the information to evaluate the fitness. If the value of fitness cannot meet the termination condition, the program will update the particle for next iteration. Through multiple iterations and judging the termination condition, we can obtain the optimal pattern automatically of the desired target.
The 1-mm thin and flexible dielectric film (F4B) with the relative permittivity 2.65 (1 + 0.003i) is used to fabricate the metasurfaces. The metal layers with thickness 0.018 mm are adopted as a kind of annealed copper (electric conductivity σ = 5.8e + 007 S/m). As depicted in Fig. 5(c), the experiment is conducted in the microwave chamber. The sample and the transmitting antenna are placed on a rotary platform, which can automatically rotate of 360° in the horizontal plane. The receiving horn antenna,connected to a vector network analyzer (Agilent N5230C), is used to measure the radiated field to obtain far-field radiation patterns.
References
Berry, D. C., Malech, R. G. & Kennedy, W. A. The reflectarray antenna. IEEE Trans. Antennas Propag 11, 645–651 (1963).
Huang, J. & Jose A. Encinar. Reflectarray Antennas, a John Wiley & Sons. Inc., Publication (2008).
Pozar, D. M., Targonski, S. D. & Pokuls, R. A shaped-beam microstrip patch reflectarray. IEEE Trans. Antennas Propag. 47, 1167–1173 (1999).
Huang, J. & Pogorzelski, R. J. A Ka-band microstrip reflectarray with elements having variable rotation angles. IEEE Trans. Antennas Propag. 46, 650–656 (1998).
Chaharmir, M. R., Shaker, J., Cuhaci, M. & Sebak, A. Reflectarray with variable slots on ground plane. IEE Proc.-Microw. Antennas Propag. 150, 436–439 (2003).
Encinar, J. A. Design of a dual frequency reflectarray using microstrip stacked patches of variable size. Electron. Lett. 32, 1049–1050 (1996).
Pozar, D. M. Bandwidth of reflectarrays. Electron. Lett. 39, 1490–1491 (2003).
Han, C., Rodenbeck, C., Huang, J. & Chang, K. AC/Ka dual frequency dual layer circularly polarized reflectarray antenna with microstrip ring elements. IEEE Trans. Antennas Propag. 52, 2871–2876 (2004).
Hsu, S. H., Han, C., Huang, J. & Chang, K. An offset linear-array-fed Ku/Ka dual-band reflectarray for planet cloud/precipitation radar. IEEE Trans. Antennas Propag. 55, 3114–3122 (2007).
Carrasco, E., Encinar, J. A. & Barba, M. Bandwidth improvement in large reflectarrays by using true-time delay. IEEE Trans. Antennas Propag. 56, 2496–2503 (2008).
Nayeri, P., Yang, F. & Elsherbeni, A. Z. Broadband reflectarray antennas using double-layer subwavelength patch elements. IEEE Antennas Wireless Propag. Lett 9, 1139–1142 (2010).
Mao, Y., Wang, C., Yang, F. & Elsherbeni, A. Z. A single-layer broad-band reflectarray design using dual-frequency phase synthesis method. Microwave Conference Proceedings (APMC), 2012 Asia-Pacific. IEEE, 64–66 (2012).
Ni, X., Emani, N. K., Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Broadband light bending with plasmonic nanoantennas. Science 335, 427–427 (2012).
Sun, S. et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett. 12, 6223–6229 (2012).
Zhang, J., Mei, Z. L., Zhang, W. R., Yang, F. & Cui, T. J. An ultrathin directional carpet cloak based on generalized Snell’s law. Appl. Phys. Lett. 103, 151115 (2013).
Li, Y., Liang, B., Gu, Z. M., Zou, X. Y. & Cheng, J. C. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Sci. Rep. 3, 2546 (2013).
Niziev, V. G. & Nesterov, A. V. Influence of beam polarization on laser cutting efficiency. J. Phys. D: Appl. Phys. 32, 1455 (1999).
Grady, N. K. et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 340, 1304–1307 (2013).
Ma, H. F., Wang, G. Z., Kong, G. S. & Cui, T. J. Broadband circular and linear polarization conversions realized by thin birefringent reflective metasurfaces. Opt. Mater. Express 4, 1717–1724 (2014).
Sun, S. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 11, 426–431 (2012).
Masajada, J. & Dubik, B. Optical vortex generation by three plane wave interference. Opt. Commun. 198, 21–27 (2001).
Beresna, M., Gecevičius, M., Kazansky, P. G. & Gertus, T. Radially polarized optical vortex converter created by femtosecond laser nanostructuring of glass. Appl. Phys. Lett. 98, 201101 (2011).
Yang, Y. et al. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Lett. 14, 1394–1399 (2014).
Bernevig, B. A., Hughes, T. L. & Zhang, S. C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Hosten, O. & Kwiat, P. Observation of the spin Hall effect of light via weak measurements. Science 319, 787–790 (2008).
Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic spin Hall effect at metasurfaces. Science 339, 1405–1407 (2013).
Cui, T. J., Qi, M. Q., Wan, X., Zhao, J. & Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light: Sci. Appl. 3, e218 (2014).
Liang, L. et al. Anomalous Terahertz Reflection and Scattering by Flexible and Conformal Coding Metamaterials. Adv. Opt. Mater. 3, 1374–1380 (2015).
Gao, L. H. et al. Broadband diffusion of terahertz waves by multi-bit coding metasurfaces. Light: Sci. Appl. 4, e324 (2015).
Liu, S. et al. Polarization-controlled anisotropic coding metamaterials at terahertz frequencies. arXiv preprint arXiv: 1509.03692 (2015).
Moessinger, A., Marin, R., Mueller, S., Freese, J. & Jakoby, R. Electronically reconfigurable reflectarrays with nematic liquid crystals. Electron. Lett. 42, 1 (2006).
Rajagopalan, H., Rahmat-Samii, Y. & Imbriale, W. A. Imbriale. RF MEMS actuated reconfigurable reflectarray patch-slot element. IEEE Trans. Antennas Propag. 56, 3689–3699 (2008).
Kennedy, J. Particle swarm optimization. Encyclopedia of machine learning. Springer US, 760–766, (2011).
Eberhart, R. & Kennedy, J. A new optimizer using particle swarm theory. Proceedings of the sixth international symposium on micro machine and human science IEEE, 39–43 (1995).
Xie, X. F., Zhang, W. J. & Yang, Z. L. Dissipative particle swarm optimization. In Evolutionary Computation, 2002. CEC'02. Proceedings of the 2002 Congress on IEEE 2, 1456-1461 (2002).
Morten, L. & Krink, T. Extending Particle Swarm Optimizers with Self-Organized Criticality. In Proc. 4th Congress on Evolutionary Computation (CEC) (2002).
Kennedy, J. & Eberhart, R. C. A discrete binary version of the particle swarm algorithm. In Systems, Man, and Cybernetics, 1997. Computational Cybernetics and Simulation. 1997 IEEE International Conference on. 5, 4104-4108 (1997).
Salman, A., Ahmad, I. & Al-Madani, S. Particle swarm optimization for task assignment problem. Microprocess. Microsy. 26, 363–371 (2002).
Sudholt, D. & Witt, C. Runtime analysis of binary PSO. Proceedings of the 10th annual conference on genetic and evolutionary computation. ACM 135-142 (2008).
Clerc, M. Discrete particle swarm optimization, illustrated by the traveling salesman problem. New optimization techniques in engineering. Springer Berlin Heidelberg, 219–239 (2004).
Yin, P. Y. A discrete particle swarm algorithm for optimal polygonal approximation of digital curves. J. Vis. Commun. Image R. 15, 241–260 (2004).
Liao, C. J., Tseng, C. T. & Luarn, P. A discrete version of particle swarm optimization for flowshop scheduling problems. Comput. Oper. Res. 34, 3099–3111 (2007).
Acknowledgements
This work was supported in part from the National Natural Science Foundation of China under Grant Nos 61401089, 61522106, 61501112, 61501117, 61571117, 61631007, and in part from the Foundation of National Excellent Doctoral Dissertation of China under Grant No. 201444.
Author information
Authors and Affiliations
Contributions
Q.Z. was responsible for the analytical modelling, software design, numerical simulations, sample fabrication, and measurements. T.J.C. provided ideas and scientific explanations. Q.Z., J.Y.Y. and L.Z. took part in performing measurements. Q.Z., X.W., S.L. and T.J.C. participated in writing the paper. All authors devoted to the preparation and the discussions.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Q., Wan, X., Liu, S. et al. Shaping electromagnetic waves using software-automatically-designed metasurfaces. Sci Rep 7, 3588 (2017). https://doi.org/10.1038/s41598-017-03764-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-03764-z
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.