Abstract
Three-dimensional confinement allows semiconductor quantum dots to exhibit size-tunable electronic and optical properties that enable a wide range of opto-electronic applications from displays, solar cells and bio-medical imaging to single-electron devices. Additional modalities such as spin and valley properties in monolayer transition metal dichalcogenides provide further degrees of freedom requisite for information processing and spintronics. In nanostructures, however, spatial confinement can cause hybridization that inhibits the robustness of these emergent properties. Here, we show that laterally-confined excitons in monolayer MoS2 nanodots can be created through top-down nanopatterning with controlled size tunability. Unlike chemically-exfoliated monolayer nanoparticles, the lithographically patterned monolayer semiconductor nanodots down to a radius of 15 nm exhibit the same valley polarization as in a continuous monolayer sheet. The inherited bulk spin and valley properties, the size dependence of excitonic energies, and the ability to fabricate MoS2 nanostructures using semiconductor-compatible processing suggest that monolayer semiconductor nanodots have potential to be multimodal building blocks of integrated optoelectronics and spintronics systems.
Similar content being viewed by others
Introduction
Semiconductor quantum dots (QDs) exhibit optical properties that can be tailored for diverse opto-electronic applications ranging from light emitting devices1, energy harvesting technologies2, and medical therapies3, to enabling rich fundamental advances in low-dimensional spintronics and quantum information processing4,5,6. In typical QDs, carrier wavefunctions are confined in all three dimensions. In the weak confinement regime, with radius R greater than the exciton Bohr radius a B, optical properties display size-tunable finite size effects in electronic structure, whereas the strong confinement (\(R\lesssim {a}_{{\rm{B}}}\)) enables discrete energy levels and fermionic exciton behavior useful for quantum devices.
The recent interest in atomically-layered transition metal dichalcogenides (TMDs) such as MoS2 has revealed a class of two-dimensional (2D) semiconductors showing strong carrier confinement in one dimension while preserving a bulk-like dispersion in the 2D plane7. Although small TMD nanoflakes made with liquid exfoliation show blue-shifted emission for reduced lateral dimensions8,9,10,11,12, the dynamics of excitonic emission in monolayer (ML) TMD nanostructures, such as laterally-confined 2D QDs (Fig. 1a), and the emergence of defect and edge states, such as seen in graphene QDs13, are not systematically well-understood. Distinct from traditional semiconductors, the spatial inversion asymmetry of the hexagonal crystal structure of ML TMD semiconductors combined with large spin-orbit coupling creates degenerate valleys in the band structure with opposite spin, Berry curvature, and effective magnetic moment14. ML TMDs thus support several internal electronic degrees of freedom in the spin and valley pseudospin14, 15. The coupled spin-valley dynamics have been extensively studied both electrically and optically16,17,18, with control over the electronic spin and valley pseudospin suggested as potential for information processing19, 20. As observed in silicon and graphene QDs4, 21,22,23,24, confinement can cause intervalley coupling and valley hybridization that render the valley pseudospin to no longer be a good quantum number. The robustness of valley polarization to lateral confinement in ML TMDs remains an open fundamental question with implications for valley control schemes (Fig. 1b,c)19, 25,26,27.
(a) Patterning of a 2D semiconductor into laterally-confined ML nanodots. (b) 2D confinement of excitons of Bohr radius a B in a potential well of radius R. (c) Spin-orbit coupling and inversion asymmetry in ML MoS2 give rise to valley-specific coupling to circularly-polarized light. Confinement can potentially enhance intervalley scattering (black lines) and suppress valley polarization.
Here, we create laterally-confined size-tunable atomically-thin TMD semiconductors through nanopatterning, demonstrating controlled continuous tuning of emission from bulk to a size scale down to 15 nm. Our measurements show that ML TMD nanodots in the weak confinement regime inherit the valley-selective band structure of the continuous ML while exhibiting controlled optical properties that depend on their lateral size. The semiconductor-compatible nanofabrication of ML nanostructures enables simultaneous tailoring of TMD optical properties and investigation of valley polarization in a regime of controlled lateral dimension with the possibility for integration into more complex devices for opto-electronic and valleytronics applications.
Results
Size-tunable optical properties
The hallmark features of confinement effects are size-dependent electronic and optical properties. We develop a top-down method to fabricate size-controlled ML MoS2 nanodots using electron beam lithography. Semiconductor processing allows for highly accurate registration of TMD nanodot patterns with respect to other features at the 10 nm length scale, while size is controlled using etching conditions. For each sample, a partial region of a continuous monolayer flake is patterned. The un-patterned monolayer region from the same exfoliated flake is used for control measurements, as shown in Fig. 2a. Figure 2b shows an atomic force microscope (AFM) image from one sample with its size distribution shown in Fig. 2c. The patterned nanodot sizes are approximately normally distributed. Samples with an average dot radius measured as small as 20 nm were fabricated, representing the weak confinement regime in which electronic properties become size-tunable. Unlike localized defects28,29,30,31 or chemically prepared TMD nanoflakes9, 10, 12, our top-down fabrication process allows control of the position and of the lateral size of the delocalized exciton in a TMD nanodot. To differentiate from TMD QDs in a strong confinement regime9, 10, 12, we refer to these patterned weakly-confined monolayers as ML nanodots. Details of the fabrication, AFM size characterization, and Raman characterization of TMD nandots are given in the Methods and Supplementary Information.
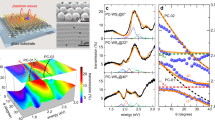
(a) Optical image of a nanopatterned sample. A 12 μm × 12 μm square of the ML MoS2 flake is processed into laterally confined nanodots. (b) AFM scan of a 1 μm × 1 μm region of patterned nanodots with dot spacing of 150 nm. (c) Nanodot size distribution from the AFM scan in (a). The size distribution is characterized by a normal distribution (red). For the sample shown, the average radius is R = 25 nm with a standard deviation of 3 nm. (d) PL spectra of nanodots (on dots, blue) and the continuous ML (off dots, black) from a single ML flake. (e) Size dependent exciton energy shift measured in ambient (blue square) and vacuum (red circle) conditions. (f) Linewidth reduction of nanodots measured in ambient (blue square) and in vacuum (red circle) conditions. All data in this figure are at room temperature.
The effect of lateral confinement on the MoS2 is measured by photoluminescence (PL) spectroscopy. A representative PL spectrum from a sample with average dot radius R = 25 nm (Fig. 2c) is shown in Fig. 2d. Compared to the un-patterned ML PL, the peak PL energy of the nanodots made from the same ML flake blue shifts and the linewidth (full width at half maximum) narrows. The unpatterned ML PL has comparable energy and linewidth to ML MoS2 exciton peaks typically identified7. The size-dependent energy shift of the nanodot PL relative to the continuous ML emission is evident in Fig. 2e. The energy shift is consistently smaller when measured in a vacuum chamber with pressure lower than 200 mTorr compared to in ambient conditions. The larger energy shift in air can be caused by adsorption of water molecules and oxygen32, which can modify monolayer electronic properties such as effective mass33 through doping and reduce the effective size of the confinement potential. Similar increased confinement and reduced effective size have been observed in semiconductor nanocrystal QDs while exposed to air34,35,36.
The size-dependent PL can be understood by considering excitons in the weak confinement regime. The modified eigenenergies of the exciton center-of-mass wavefunction are estimated from the envelope function approach by approximating the nearly-circular ML nanodots as a two-dimensional axisymmetric infinite potential of radius R. Lateral 2D confinement leads to a 1/R 2 dependence for the exciton energy levels37, 38. The envelope function approach is a good approximation in the weak confinement regime (\(R\gg {a}_{B}\)) when the exciton has large binding energy and the internal levels can be ignored38. This is valid for ML MoS2, in which a B ~ 1 nm is small compared to the patterned radius in our experiment and the exciton binding energy is approximately 0.9 eV33, 39. In the weak confinement regime here, the center-of-mass confinement manifests as a shift in the emission rather than resolved energy levels familiar from strongly confined QDs.
Motivated by the center-of-mass energy levels of weakly confined QDs, the size-dependent PL energy shift of the patterned nanodots is characterized by a phenomenological inverse square function
Here, E0 is the PL energy without in-plane confinement (including binding energy), ħ is the reduced Planck’s constant, R − ΔR is the effective nanodot radius, \({\rho }_{0}\simeq 2.4048\) is the first root of the zero-order Bessel function, and \({M}_{{\rm{ex}}}^{\ast }\) is an effective mass fit parameter. Since the dot size measured by AFM is a convolution of the tip and dot geometry, and the reactive etching process or environment can alter the electronic properties of the monolayer edge, the effective nanodot radius can be several nanometers smaller than the measured size (see Supplementary Information). Measurements in both ambient and vacuum conditions show a shift of effective radius ΔR ~ 8 nm and are otherwise consistent with the 1/R 2 confinement behavior. The mass \({M}_{{\rm{ex}}}^{\ast }\) in vacuum (ambient) is extracted from the fit to be M ex = 0.12 ± 0.03 m 0 (0.058 ± 0.006 m 0), where m 0 is the free electron mass. The difference between the ambient and vacuum parameters suggests that the nanodots are influenced by adsorption from the environment32, which would be expected to be increasingly significant in nanostructures with increased surface-to-volume ratio. Photocarrier relaxation processes from the non-equilibrium optical excitation impact the observed emission energy shift. The energy scaling is also influenced by electron-electron interactions, doping, strain, and dielectric environment, all of which are known to influence monolayer electronic properties33, 39,40,41,42,43. Additional discussion of the energy shift is provided in the Supplementary Information.
The PL linewidth Γ decreases with confinement compared to the linewidth in un-patterned MoS2 ML as shown in Fig. 2f. The linewidth reduction is larger for smaller nanodots, with the narrowest linewidth measured to be about 25 meV smaller compared to a typical MoS2 ML PL linewidth. The reduction measured in vacuum is smaller compared to that in ambient conditions. Although the difference between vacuum and ambient conditions warrants further investigation, the 1/R 2 dependence of the exciton energy shift and narrower PL linewidth demonstrate controlled lateral size-dependent effects in a TMD monolayer.
Temperature dynamics of laterally confined nanodots
Figure 3a shows low-temperature PL spectra collected when the excitation is either on the dots or the continuous ML control region. A peak at about 1.9 eV and a low-energy state at 1.77 eV are evident. The peak energy and lineshape are both consistent with ML exciton emission reported in other studies44,45,46. ML MoS2 is well-known to exhibit lower-energy bound state luminescence at low temperatures47, 48. The lateral confinement in our nanodots does not modify the energy of this bound state PL at 1.77 eV, indicating that the bound state is formed by localized defect states49 rather than free band excitons. Temperature dependence of the emission energy and linewidth are shown in Fig. 3b. The energy difference between ML and nanodots is independent of temperature, consistent with the shift arising from a size-dependent confinement energy rather than thermally-activated defect doping or redistribution of trion and exciton populations. Additional discussion of the PL behavior appears in the Supplementary Information.
PL spectra characterization. (a) The PL of the nanodots (red) and continuous ML (blue) at 6 K both show features of excitonic and low-energy bound state emission. (b) Temperature dependence of the exciton energy E ex (solid) and linewidth Γ (empty) for nanodots (circles) and ML (squares). The lines are fits to the Manoogian-Wooley equation62 and Eq. (2), respectively.
The linewidth Γ provides information on homogeneous broadening and inhomogeneity of the material43, 50. At low temperatures, the homogeneous linewidth is dominated by the acoustic (AC) phonon dephasing that scatters excitons to intraband states. At higher temperatures, the longitudinal optical (LO) phonon interaction scatters excitons to both bound and continuum states, with contribution to the linewidth proportional to LO phonon number50, 51. Neglecting any screening and doping effects specific to ML materials, the temperature dependence of Γ for excitons in a continuous dispersion band can be expressed as
where Γ0 includes the inhomogeneous and radiative linewidth, γ AC and γ LO are the exciton-AC and exciton-LO phonon coupling strengths, and E LO is the LO phonon energy.
Figure 3b shows fits of the linewidth of continuous ML and nanodots to Eq. (2). As with emission energy, the temperature dynamics of Γ are similar for both ML and nanodot regions, but Γ for the nanodots is somewhat reduced (details of the fits are in the Supplementary Information). Inhomogeneous broadening in Γ0 is expected to be much larger than the small intrinsic linewidth43 and will dominate the overall linewidth Γ. Γ0 is similar in ML and nanofalkes (Γ0 is 67 ± 1 meV and 65 ± 1 meV, respectively), suggesting that unintentional doping from fabrication is not influencing emission. Rather, the inhomogeneities are caused by local disorder potentials from lattice, surface, and substrate defects that remain significant across the wavefunction scale. Broad PL linewidths have also been reported in single chemically-exfoliated nanoflakes in a stronger confinement regime, so confinement with controlled nanopatterning in the regime here is not expected to narrow the low temperature exciton linewidth12.
The change of the PL linewidth of the nanodot ensemble is determined by two competing mechanisms. Confinement narrows the homogeneous linewidth by reducing the available acoustic phonon states, whereas the inhomogeneous size distribution broadens the linewidth. We indeed find that the γ AC in the nanodots (12 μeV/K) is smaller than that in the monolayer (42 μeV/K). The 10% width of the nanodot size distributions (Fig. 2b) introduces a 20% variation in confinement energy due to the 1/R 2 dependence. Because of the small energy shifts in this regime, the size distribution only causes less than 2 meV of broadening. This interpretation is supported by measurement of PL from a few WSe2 nanodots, which also shows a similarly broad linewidth (see Supplementary Information). The reduction of Γ at high temperatures implies that the confinement effects dominate the inhomogeneous broadening introduced by fabrication, consistent with observations in other confined systems such as GaAs51,52,53.
Similar lithographically-defined laterally confined structures have been etched from semiconductor quantum wells. In contrast to the monolayer TMD nandots, the etched quantum wells typically exhibit non-radiative PL broadening54, 55. This non-radiative broadening originates from defects at the etched sidewall edges. The weakly confined excitons of the TMD, with Bohr radius a B ~ 1 nm, are less sensitive to edge defects and surface chemistry than in conventional quantum wells with larger Bohr radius typically on the order of 10 nm; phonon processes dominate over edge effects in the TMD nanodots. Smaller chemically exfoliated TMD nanoflakes in the strong confinement regime do exhibit non-radiative broadening likely from exciton coupling to surface defects similar to etched quantum wells12.
Valley polarization in weakly confined monolayer MoS2 nanodots
The spin-orbit coupling and inversion asymmetry in the TMD monolayer allow selective optical excitation of different valleys using circularly polarized light, which can be detected as circularly-polarized PL emission14, 16, 17. Valley hybridization from intervalley scattering can reduce emission polarization, as would be expected at elevated temperatures or near monolayer edges16, 44. To investigate the impact of quantum confinement on valley hybridization in MoS2 nanodots, we measure polarized PL.
Figure 4 shows polarized PL measured on and off nanodots with R = 25 nm using two different pump energies, 2.07 eV and 2.00 eV. The spectrally-resolved PL polarization is defined by
where I + and I − are the right (σ +) and left (σ −) circular polarization-resolved PL spectral intensities. The nanodot emission exhibits similar polarization to that of the ML for each pump energy as shown in Fig. 4c,f. The slightly smaller nominal nanodot polarization is due to the higher relative intensity of the tail from the unpolarized low-energy bound state at 1.77 eV and the background. After subtracting a fit to the bound state PL and background, we observe almost identical (within our measurement accuracy) pump-dependent polarization of nanodot and ML emission as shown in Fig. 4g, where the polarization is calculated similarly to Eq. (3) but using the integrated intensities of the exciton PL peak. For both nanodots and ML, the polarization increases for pump energy closer to the exciton resonance. The pump energy dependence (Fig. 4g) can be characterized by a phenomenological exponential curve \(P\sim \exp \,[-({E}_{{\rm{pump}}}-{E}_{{\rm{ex}}})/\xi ]\), where E pump is the pump energy, E ex is the exciton energy, and ξ describes the energy decay scale. The fit to nanodots and ML show similar decay scale ξ = 0.074 ± 0.006 (0.079 ± 0.013) eV. The pump energy dependence of P is similar to that previously reported for MoS2 and associated with acoustic phonon-driven intervalley scattering45. Figure 4h shows the difference of emission polarization between nanodots and continuous ML sheet for varying nanodot size. Within the measurement precision, nearly unchanged polarization is observed across all the nanodot sizes.
Valley polarization characterization from a continuous ML and nanodots. (a,b) Circularly-polarized emission with pump energy of 2.07 eV. (c) Polarization P of PL with pump energy of 2.07 eV. (d,e) Circularly polarized PL with pump energy of 2.00 eV. (f) Polarization P with pump energy 2.00 eV. (g) Pump energy dependence of the continuous ML (off dots) and nanodots (on dots). The characteristic energy exponential decay scale is ξ = 74 meV for nanodots (red) and ξ = 79 meV for a continuous ML (blue). (h) The negligible change in PL circular polarization with confinement is independent of nanodot size. Polarization is measured with pump energy at 2.00 eV for (g,h). PL in this figure is collected at 6 K.
The persistence of valley polarization in weakly confined ML TMD quantum dots is expected from theoretical predictions25. Despite the strong dependence of intervalley scattering on confinement potential, the upper bound of the intervalley coupling in ML MoS2 dots is 0.1 meV for small sizes (20 nm in diameter)25 which is negligible compared to the energy difference between the same spin states in different valleys, for both electrons (several meV)56 and holes (~150 meV)14, 56. Therefore, valley polarization is expected to be only weakly perturbed in this size nanodot. Although in graphene nanoribbons a width of 30 nm is enough to create tens of meV valley splitting4, excitons in TMD nanodots exhibit weaker wavefunctions near the boundaries where intervalley coupling is significant, leading to correspondingly weaker valley hybridization25. Our observation of valley-polarized emission in quantum confined ML nanodots confirms the theoretical prediction of Liu25 that intervalley scattering is negligibly increased in ML MoS2 dots with radii as low as 15 nm.
Discussion
The evolution of valley polarization in TMD nanostructures with lateral confinement has not been explored in previous experiments. Polarized PL is not reported from highly confined monolayer nanoflakes8,9,10,11,12. Our work demonstrates that lateral confinement does not measurably increase intervalley scattering in ML MoS2 dots down to the size of 15 nm, illuminating optical behavior in this intermediate size-dependent regime. If the valley polarization is unperturbed by even stronger lateral confinement, ML TMD nanostructures might be a viable platform for exploring the valley degrees of freedom of a single electron20. The techniques required to achieve strong lateral confinement in smaller patterned monolayer nanostructures and the new quantum phenomena and edge effects that would arise in this regime19, 26, 27 are beyond the scope of this work.
The controlled size-dependence of low-dimensional excitons is an important consequence of lateral confinement useful for many applications of semiconductor nanomaterials and heterostructures57,58,59,60. Our nanofabrication approach enables size-tunable lateral confinement in ML MoS2 nanodots using a controllable top-down semiconductor-compatible fabrication process. The size-dependent, but temperature independent, energy shift indicates that its origin is not unintentional edge or fabrication doping. Recently, quantum emitters in 2D TMDs have been demonstrated from defect states in monolayer WSe2 28,29,30,31. Although interesting for quantum information applications, these randomly distributed localized states do not exhibit size-dependent excitonic properties indicative of lateral confinement or the valley polarization of excitons in the monolayer TMD band structure. Distinct from these defect emitters, our results demonstrate controlled size-dependent confinement of delocalized band carriers. Since excitons in monolayer TMDs have very large binding energies and small Bohr radii (a B ~ 1 nm), it is challenging to reach a strong confinement regime with an anharmonic spectrum and antibunched emission using top-down processing.
Systematic control of size in TMD nanodots allows exploration of the optical properties of isolated ML nanostructures. Our work demonstrating size-tunable lateral confinement is a first step toward control of three-dimensional confinement in monolayer semiconductors. The inheritance of ML valley properties in ML semiconductor nanodots with size-controlled exciton energies suggests that TMD ML nanostructures are a potential platform for harnessing the valley degree of freedom of a single electron19, 20, 25. Extending semiconductor-compatible nanofabrication of laterally-confined ML nanodots with controlled size-dependent features can help to realize low-dimensional building blocks for integrated opto-electronic systems11 based on spin and valley.
Methods
Sample preparation
ML MoS2 flakes are obtained from a bulk crystal (SPI Supplies) using mechanical exfoliation. The flakes are dry transferred onto a SiO2/Si substrate with pre-written alignment marks61. Identification of ML MoS2 is done using atomic force microscopy (AFM), optical contrast, and PL spectroscopy following documented procedures61. Samples are annealed in an Ar/H2 environment at 400 ºC before patterning with electron beam lithography and reactive ion etching using CHF3/O2 gas. The resist is not removed at the end of processing to prevent destruction of the ML nanodots. Additional sample fabrication and material characterization details can be found in the Supplementary Information.
Optical measurement
PL characterization was performed with a 532 nm semiconductor laser, and near-resonant circularly-polarized PL is measured with a tunable pulsed femotosecond optical parametric oscillator whose linewidth was narrowed to approximately 1 nm using a double-grating system. The pump laser is focused through a 100× long-working distance objective with numerical aperture of 0.65 and a spot size near 1 μm. The pump power is kept less than 40 μW to suppress heating effects. The sample is mounted in a closed-cycle cryostat capable of reaching temperatures between 4 K and 350 K. The objective can be scanned across the sample with sub-micron resolution. The PL is collected through the same objective and analyzed by a spectrometer with a CCD. Energy and linewidth shifts for nanodots are reported relative to the continuous ML control region from the same exfoliated flake. The low areal density of the sparse array pattern precludes absorption measurements of the processed monolayer nanodots. For circularly-polarized PL, the samples are stabilized at 6 K. The pump polarization is controlled using a linear polarizer and a liquid crystal retarder. The emitted PL is analyzed using a quarter waveplate and a linear polarizer before being coupled into the spectrometer. The polarization of the pump laser is measured to be greater than 99.5% with this apparatus. Reported best-fit parameters are obtained from weighted least-squares fitting with parameter uncertainties estimated using resampling.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Sun, Q. et al. Bright, multicoloured light-emitting diodes based on quantum dots. Nature Photon. 1, 717–722 (2007).
Kramer, I. J. & Sargent, E. H. The architecture of colloidal quantum dot solar cells: Materials to devices. Chem. Rev. 114, 863–882 (2013).
Azzazy, H. M. E., Mansour, M. M. H. & Kazmierczak, S. C. From diagnostics to therapy: Prospects of quantum dots. Clin. Biochem. 40, 917–927 (2007).
Trauzettel, B., Bulaev, D. V., Loss, D. & Burkard, G. Spin qubits in graphene quantum dots. Nature Phys. 3, 192–196 (2007).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120 (1998).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Kang, J. et al. Thickness sorting of two-dimensional transition metal dichalcogenides via copolymer-assisted density gradient ultracentrifugation. Nature Commun. 5 (2014).
Gan, Z. X. et al. Quantum confinement effects across two-dimensional planes in MoS2 quantum dots. Appl. Phys. Lett. 106, 233113 (2015).
Gopalakrishnan, D. et al. Electrochemical synthesis of luminescent MoS2 quantum dots. Chem. Commun. 51, 6293–6296 (2015).
Mukherjee, S., Maiti, R., Katiyar, A. K., Das, S. & Ray, S. K. Novel colloidal MoS2 quantum dot heterojunctions on silicon platforms for multifunctional optoelectronic devices. Sci. Rep. 6 (2016).
Jin, H. et al. Colloidal single-layer quantum dots with lateral confinement effects on 2D exciton. J. Am. Chem. Soc. 138, 13253–13259 (2016).
Lee, J. et al. Uniform graphene quantum dots patterned from self-assembled silica nanodots. Nano Letters 12, 6078–6083 (2012).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nature Phys. 10, 343–350 (2014).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nature Nanotech. 7, 490–493 (2012).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nature Nanotech. 7, 494–498 (2012).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Kormányos, A., Zólyomi, V., Drummond, N. D. & Burkard, G. Spin-orbit coupling, quantum dots, and qubits in monolayer transition metal dichalcogenides. Phys. Rev. X 4, 011034 (2014).
Wu, Y., Tong, Q., Liu, G.-B., Yu, H. & Yao, W. Spin-valley qubit in nanostructures of monolayer semiconductors: Optical control and hyperfine interaction. Phys. Rev. B 93, 045313 (2016).
Goswami, S. et al. Controllable valley splitting in silicon quantum devices. Nature Phys. 3, 41–45 (2007).
Saraiva, A. L., Calderón, M. J., Hu, X., Sarma, S. D. & Koiller, B. Physical mechanisms of interface-mediated intervalley coupling in Si. Phys. Rev. B 80, 081305 (2009).
Han, M. Y., Özyilmaz, B., Zhang, Y. & Kim, P. Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 98, 206805 (2007).
Libisch, F., Rotter, S., Güttinger, J., Stampfer, C. & Burgdörfer, J. Transition to Landau levels in graphene quantum dots. Phys. Rev. B 81, 245411 (2010).
Liu, G.-B., Pang, H., Yao, Y. & Yao, W. Intervalley coupling by quantum dot confinement potentials in monolayer transition metal dichalcogenides. New J. Phys. 16, 105011 (2014).
Pavlović, S. & Peeters, F. M. Electronic properties of triangular and hexagonal MoS2 quantum dots. Phys. Rev. B 91, 155410 (2015).
Pei, L., Tao, S., Haibo, S. & Song, X. Structural stability, electronic and magnetic properties of MoS2 quantum dots based on the first principles. Solid State Commun. 218, 25–30 (2015).
He, Y.-M. et al. Single quantum emitters in monolayer semiconductors. Nature Nanotech. 10, 497–502 (2015).
Srivastava, A. et al. Optically active quantum dots in monolayer WSe2. Nature Nanotech. 10, 491–496 (2015).
Koperski, M. et al. Single photon emitters in exfoliated WSe2 structures. Nature Nanotech. 10, 503–506 (2015).
Chakraborty, C., Kinnischtzke, L., Goodfellow, K. M., Beams, R. & Vamivakas, A. N. Voltage-controlled quantum light from an atomically thin semiconductor. Nature Nanotech. 10, 507–511 (2015).
Late, D. J., Liu, B., Matte, H. R. S. R., Dravid, V. P. & Rao, C. N. R. Hysteresis in single-layer MoS2 field effect transistors. ACS Nano 6, 5635–5641 (2012).
Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012).
Cordero, S. R., Carson, P. J., Estabrook, R. A., Strouse, G. F. & Buratto, S. K. Photo-activated luminescence of CdSe quantum dot monolayers. J. Phys. Chem. B 104, 12137–12142 (2000).
van Sark, W. G. J. H. M. et al. Photooxidation and photobleaching of single CdSe/ZnS quantum dots probed by room-temperature time-resolved spectroscopy. J. Phys. Chem. B 105, 8281–8284 (2001).
Sykora, M. et al. Effect of air exposure on surface properties, electronic structure, and carrier relaxation in PbSe nanocrystals. ACS Nano 4, 2021–2034 (2010).
Bera, N., Bhattacharjee, J. K., Mitra, S. & Khastgir, S. P. Energy levels of a particle confined in a super-circular box. Eur. Phys. J D 46, 41–50 (2008).
Woggon, U. Optical Properties of Semiconductor Quantum Dots (Springer, 1997).
Cheiwchanchamnangij, T. & Lambrecht, W. R. L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 85, 205302 (2012).
Peelaers, H. & Van de Walle, C. G. Effects of strain on band structure and effective masses in MoS2. Phys. Rev. B 86, 241401 (2012).
Ugeda, M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nature Mater. 13, 1091–1095 (2014).
Lin, Y. et al. Dielectric screening of excitons and trions in single-layer MoS2. Nano Letters 14, 5569–5576 (2014).
Moody, G. et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nature Commun. 6, 8315 (2015).
Lagarde, D. et al. Carrier and polarization dynamics in monolayer MoS2. Phys. Rev. Lett. 112, 047401 (2014).
Kioseoglou, G. et al. Valley polarization and intervalley scattering in monolayer MoS2. Appl. Phys. Lett. 101, 221907 (2012).
Sallen, G. et al. Robust optical emission polarization in MoS2 monolayers through selective valley excitation. Phys. Rev. B 86, 081301 (2012).
Korn, T., Heydrich, S., Hirmer, M., Schmutzler, J. & Schüller, C. Low-temperature photocarrier dynamics in monolayer MoS2. Appl. Phys. Lett. 99, 102109 (2011).
Tongay, S. et al. Defects activated photoluminescence in two-dimensional semiconductors: Interplay between bound, charged, and free excitons. Sci. Rep. 3, 2657 (2013).
Hong, J. et al. Exploring atomic defects in molybdenum disulphide monolayers. Nature Commun. 6, 6293 (2015).
Rudin, S., Reinecke, T. L. & Segall, B. Temperature-dependent exciton linewidths in semiconductors. Phys. Rev. B 42, 11218 (1990).
Zhao, H., Wachter, S. & Kalt, H. Effect of quantum confinement on exciton-phonon interactions. Phys. Rev. B 66, 085337 (2002).
Bockelmann, U. & Bastard, G. Phonon scattering and energy relaxation in two-, one-, and zero-dimensional electron gases. Phys. Rev. B 42, 8947–8951 (1990).
Borri, P., Langbein, W., Hvam, J. M. & Martelli, F. Well-width dependence of exciton-phonon scattering in In x Ga1−x As/GaAs single quantum wells. Phys. Rev. B 59, 2215 (1999).
Verma, V. B. & Coleman, J. J. High density patterned quantum dot arrays fabricated by electron beam lithography and wet chemical etching. Appl. Phys. Lett. 93, 111117, (2008).
Lee, L. K., Zhang, L., Deng, H. & Ku, P.-C. Room-temperature quantum-dot-like luminescence from site-controlled InGaN quantum disks. Appl. Phys. Lett. 99, 263105, (2011).
Liu, G.-B., Shan, W.-Y., Yao, Y., Yao, W. & Xiao, D. Three-band tight-binding model for monolayers of group-VIB transition metal dichalcogenides. Phys. Rev. B 88, 085433 (2013).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Cheng, R. et al. Electroluminescence and photocurrent generation from atomically sharp WSe2/MoS2 heterojunction p-n diodes. Nano Letters 14, 5590–5597 (2014).
Yu, W. J. et al. Highly efficient gate-tunable photocurrent generation in vertical heterostructures of layered materials. Nature Nanotech. 8, 952–958 (2013).
Novoselov, K. S. & Neto, A. H. C. Two-dimensional crystals-based heterostructures: Materials with tailored properties. Physica Scripta 2012, 014006 (2012).
Wei, G., Stanev, T. K., Czaplewski, D. A., Jung, I. W. & Stern, N. P. Silicon-nitride photonic circuits interfaced with monolayer MoS2. Appl. Phys. Lett. 107, 091112 (2015).
Manoogian, A. & Woolley, J. Temperature dependence of the energy gap in semiconductors. Can. J. Phys. 62, 285–287 (1984).
Acknowledgements
This work is supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering (DE-SC0012130) (dot spectroscopy), the Institute for Sustainability and Energy at Northwestern (device fabrication), and Argonne National Laboratory. This work was partially supported (sample characterization) by the National Science Foundation’s MRSEC program (DMR-1121262) and made use of its Shared Facilities at the Materials Research Center of Northwestern University. Use of the Center for Nanoscale Materials was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. Characterization and device fabrication made use of the EPIC and SPID facilities of the NUANCE Center at Northwestern University and the Northwestern University Micro/Nano Fabrication Facility (NUFAB), which have received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF NNCI-1542205); the MRSEC program (NSF DMR-1121262) at the Materials Research Center; the International Institute for Nanotechnology (IIN); the Keck Foundation; and the State of Illinois. The authors thank S. Davis and V. Chandrasekhar for assistance with facilities and instrumentation. N.P.S. gratefully acknowledges support as an Alfred P. Sloan Research Fellow.
Author information
Authors and Affiliations
Contributions
N.P.S. and G.W. conceived the experiments. G.W., D.C., and I.J. developed the sample fabrication process. E.J.L. and T.K.S. assisted with sample fabrication and characterization. G.W. conducted the measurements and the modelling. G.W. and N.P.S. co-wrote the paper. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wei, G., Czaplewski, D.A., Lenferink, E.J. et al. Size-tunable Lateral Confinement in Monolayer Semiconductors. Sci Rep 7, 3324 (2017). https://doi.org/10.1038/s41598-017-03594-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-03594-z
This article is cited by
-
Confinement of excited states in two-dimensional, in-plane, quantum heterostructures
Nature Communications (2024)
-
Coupled Charge Transfer Dynamics and Photoluminescence Quenching in Monolayer MoS2 Decorated with WS2 Quantum Dots
Scientific Reports (2019)
-
Material platforms for spin-based photonic quantum technologies
Nature Reviews Materials (2018)
-
Emerging nanofabrication and quantum confinement techniques for 2D materials beyond graphene
npj 2D Materials and Applications (2018)
-
Environmental engineering of transition metal dichalcogenide optoelectronics
Frontiers of Physics (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.