Abstract
Dielectric multilayer structures with a grating profile on the top-most layer adds an additional degree of freedom to the phase matching conditions for Bloch surface wave excitation. The conditions for Bloch surface wave coupling can be achieved by rotating both polar and azimuthal angles. The generation of Bloch surface waves as a function of azimuthal angle has similar characteristics to conventional grating coupled Bloch surface waves. However, azimuthally generated Bloch surface waves have enhanced angular sensitivity compared to conventional polar angle coupled modes, which makes them appropriate for detecting tiny variations in surface refractive index due to the addition of nano-particles such as protein molecules.
Similar content being viewed by others
Introduction
Bloch surface waves (BSW) are electromagnetic modes propagating at the interface of truncated dielectric multilayer structures and a homogeneous medium. The resonant generation of these modes via prism or grating coupling is an active field of current research. Following the prediction1 and experimental observation2 of BSWs in photonic crystals, these modes have been studied, both theoretically and experimentally, in various configurations3,4,5,6. The resulting strong field/energy localization at the surface layer and the evanescently extending field in the homogeneous medium are of interest in applications such as label-free biosensing based on enhanced diffraction7,8,9, surface-enhanced Raman spectroscopy10, 11, spectral and angular resonance shift12,13,14,15,16, fluorescence-based detection17,18,19,20, slow-light enhanced nonlinear effects21, 22, integrated optical circuits23, and optical slow-light devices and sensors24, 25. BSWs are evanescent in nature; they are perfectly bound non-radiative states that lie below the light line of the homogeneous layer material. However, it was recently shown that if the surface layer is periodically corrugated and the dielectric constant of the dielectric medium is real, positive, and large, it can support a leaky BSW26. Such leaky modes still lie below the light line of the homogeneous layer material but fall above that of the dielectric multilayer material. As a result, this leaky BSW is bound to the surface in the homogeneous region but is radiative into the dielectric multilayer. Moreover, under appropriate conditions, it is possible to excite photonic surface states inside the radiation continuum27,28,29. Although these states are radiative into the homogeneous medium, they can have a long lifetime assisted by destructive interference between different leakage channels. Such leaky-mode resonances, with moderate to infinitely high quality factor (Q) that confine freely propagating electromagnetic waves at a periodically modulated surface, are of interest in applications such as lossless mirrors30, high-performance optical filters31, label-free biosensors32, dielectric metasurfaces33, 34, dielectric-based optical magnetism35, and many others36, 37.
In this paper, we show through computational simulation that moderate-Q leaky BSWs on a dielectric multilayer surface with periodic corrugation can be used to significantly enhance the sensitivity of biosensors. To enhance the sensitivity we take advantage of the fact that the periodic corrugation of the surface layer allows us an additional degree of freedom over the azimuthal angle of the incident beam, which is not possible on a planar uncorrugated surface. In an experimental setup, this additional degree of freedom can be accessed by rotating the multilayer platform itself azimuthally. To our best knowledge however, little has been done in this regards38, 39. Previous related studies were done on surface plasmon polaritons (SPPs)—electromagnetic modes propagating at the interface of a metal and a dielectric medium—where the reflectivity is measured by fixing the azimuthal angle to a certain value followed by the conventional polar incident angle sweep. Here we propose a new technique of sensing using leaky BSWs, wherein we fix the polar incident angle to a specific value and then sweep over the azimuthal angle to fulfill the phase matching requirement to excite leaky BSWs. The advantages of this technique are twofold. First, it mitigates the requirement of a bulky prism to excite BSWs and thus affords the opportunity to engineer nanoscale lab-on-chip biosensors. Second, it can be used to make polarization independent biosensors, due to the fact that a linear grating profile facilitates polarization conversion40,41,42.
Computational Method
A schematic of the computational setup considered in this study is shown in Fig. 1. We use a sixteen layered TiO2-SiO2 multilayer on a SiO2 substrate. The grating profile on the surface of the SiO2 layer is SiO2 as well. We consider the wavelength (λ) dependent refractive index of both TiO2 43 and SiO2 44 over the range of 0.43 μm to 0.8 μm as given by:
and
respectively. In the rest of the paper however, λ is given in nm. The index value of SiO2 films is well established. For TiO2 the presence of voids can reduce the index from that predicted; however, with careful fabrication45, the values used here are valid. There is ample evidence in the experimental literature that such multilayers, including those with surface grating structures2, 4, 12, 13, 20, 23, can be readily fabricated.
The thicknesses of TiO2 and SiO2 layers are 126.13 nm and 205.41 nm respectively. The excitation and confinement of BSWs on the surface of one-dimensional (1D) photonic crystals are highly sensitive to the thickness of the surface defect layer due to the effects of multiple reflections from the periodic dielectric multilayer beneath46. For this reason, we set the thickness of the top SiO2 layer to 280.03 nm. The grating height is set to 70 nm with a fill factor of 0.5a, where a is the grating period set to 510 nm. The refractive index of the superstrate layer (n sup) considered in our study is 1.26–1.4. The polar incident angle (θ inc) is measured relative to the surface normal, while the azimuthal angle (ϕ) is measured with respect to the plane perpendicular to the grating profile.
We use an in-house three-dimensional (3D) scattering-matrix-based rigorous coupled wave analysis (SMRCWA) method to simulate the electric/magnetic field (TE-polarized) distribution in the computational domain containing the multilayer structure, the SiO2 substrate, and the superstrate. The incident electric and magnetic fields are expressed in their Fourier expansion as
where
\({k}_{{\rm{x}},{\rm{inc}}}=\frac{2\pi }{\lambda }{n}_{{\rm{\sup }}}\sin ({\theta }_{{\rm{inc}}})\cos (\varphi )\) and \({k}_{{\rm{y}},{\rm{inc}}}=\frac{2\pi }{\lambda }{n}_{{\rm{\sup }}}\sin ({\theta }_{{\rm{inc}}})\sin (\varphi )\) are the x and y components of k inc. Λx = a is the grating period in the x direction. The structure considered in this paper does not have any periodicity in the y direction. Thus Λy can be set to any non-zero value. For simplicity however, here we set Λy = a as well. S m,n(z) and U m,n(z) in Eqns (3) and (4) are the Fourier coefficients, which can be computed by solving Maxwell’s equations in Fourier space. The method is described in detail in Supplementary notes 1.
To verify the results obtained from the 3D SMRCWA method, we also do a 3D implementation of the structure in the commercial Finite Element Method software COMSOL Multiphysics. The results from both the methods are in good agreement. Moreover, the dispersion curves and the mode profiles were verified using Meep (an open source finite-difference time-domain (FDTD) software from MIT) as well.
Results & Discussion
The proposed method consists in taking advantage of the surface grating profile, as illustrated in Fig. 1, to achieve sensing by selectively exciting BSWs via azimuthal interrogation. It is crucial to realize BSWs first in a setting where ϕ = 0°. A cross-section of a one period structure for this purpose is shown in Fig. 2(a). The surface grating serves as an input coupler that couples a plane wave (PW) into BSW mode. This BSW mode excitation is assisted by the constructive interference of PWs. At the correct incidence angle and groove spacing, a maximum coupling of the PWs to the BSW mode on the grating can be achieved, as summarized by Eqn. (7).
where k 0 = 2π/λ and k BSW are the magnitudes of the free space wave vector and grating BSW wave vector respectively, n sup is the refractive index of the superstrate, θ inc is the incident angle, a is the grating period, and m is an integer47.
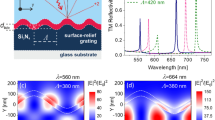
Leaky Bloch surface wave at ϕ = 0°. (a) TiO2-SiO2 multilayer with grating on the top layer. (b) Dispersion curves of the leaky BSWs supported by the structure. The green region is the radiative region (c,d) Reflectance of BSW as a function of incident angle and wavelength respectively. (e,f) Electric field profiles of BSW modes. The red and blue circles at the resonance peaks represent the reflectance at the corresponding circles in (b).
To excite grating-coupled BSWs for a given incident wavelength, the grating period a is chosen such that there is at least one angle that satisfies Eqn. (7), which leads to \(\lambda /a < {k}_{{\rm{BSW}}}/{k}_{0}+1\). In this paper, we choose m = 1 and θ inc > 0, such that \(2\pi /a > {k}_{{\rm{BSW}}}\). Given that \({k}_{BSW} > {k}_{0}\), we get \(\lambda /a/ > {k}_{{\rm{BSW}}}/{k}_{0} > 1\). Therefore, the range of appropriate grating periods can be summarized as \({k}_{{\rm{BSW}}}/{k}_{0} < \lambda /a < {k}_{{\rm{BSW}}}/{k}_{0}+1\).
The surface mode band structures of BSW modes for the structure are shown in Fig. 2(b). By terminating the surface layer with an additional thickness to act as a defect, we can create a platform for exciting BSWs. By etching a grating profile on top of it, we can mitigate the necessity of a prism to excite them. Periodicity on the surface plays an important role on these modes. The evanescent fields in the superstrate layer, in the presence of periodicity, can have wavevectors k x in the reciprocal lattice that are integer multiples of 2π/a, resulting in BSW resonances. We observe two distinct BSW modes, highlighted in red and blue, in Fig. 2(b). Reflectivity curves of these modes, as a function of angle of incidence and wavelength, are shown in Fig. 2(c,d) respectively, where the colored tips correspond to their respective colored circle marks in Fig. 2(b). As can be seen in these figures, these modes have sharp resonance features at their excitation both as a function of angle and wavelength. Figure 2(e,f) show the field profile E y of the BSW modes at the red (λ = 660 nm) and blue (λ = 710 nm) circles in Fig. 2(b) at \({\theta }_{{\rm{inc}}}\approx {2.5}^{\circ }\). At these surface-parallel wavevectors near \({k}_{{\rm{x}},{\rm{inc}}}\approx 0.04\times 2\pi /a\), the E y field is highly confined to the surface giving rise to the BSW modes. We can also see a slight leakage in the superstrate layer. Time-domain field profiles of these modes are shown in Supplementary Videos 1 and 2. The direction of propagation of these modes in Fig. 2(d,e) are opposite however, which can be clearly seen in their time-domain profiles (see Supplementary Videos 1 and 2). This difference in the direction of propagation can be explained by the opposite sign slopes of the red and blue BSW modes in Fig. 2(b). These modes are different than conventional BSW modes as they exist in the radiative region. BSWs in general, only exist in the non-radiative region where they are perfectly bound to the surface. The BSW modes under consideration in this paper are not perfectly bound and are somewhat leaky. However, the quality factor (\(Q=\omega \tau /2=(1/{Q}_{{\rm{r}}})+(1/{Q}_{{\rm{nr}}})\), where Q r and Q nr are the normalized radiative and non-radiative lifetimes due to leakage into free space) of these modes are high enough \((Q\approx 6000)\) that they can safely be used for practical applications in bio-sensing. The resonance lifetimes are extracted from the Fano features28 by fitting the reflectivity of the grating coupled multilayer structure to the thin-film reflectivity with the Fano features described by
where ω 0 is the resonance frequency, and r slab and t slab are the reflection and transmission coefficients of a homogeneous slab, respectively. We further confirmed the quality factors of these modes using 2D FDTD simulations with point-dipole sources on the surface to perform harmonic analysis to compute the lifetime τ and Q of these resonant modes. The FDTD simulations were only performed for ϕ = 0°. The superstrate and substrate layers were terminated by perfectly matched layers, whereas the side boundaries were considered to be Floquet periodic boundaries. The mesh resolution was set to about 120 pixels per wavelength.
The previous paragraphs outline the conditions for coupling to BSWs by varying the polar angle, θ inc, with ϕ = 0°. We now examine the effect of altering the azimuthal angle ϕ to achieve BSW excitation. For this study we chose wavelengths in the vicinity of 632.8 nm corresponding to an experimental realization with a Helium-Neon laser. In this analysis the polar angle of the incident light was set to θ inc = 5.4°. This angle is slightly greater than the resonant angle for polar coupling θ BSW = 5.2°. The parallel wave vector of the incident light, allowing for variable ϕ, is given by \({k}_{x,\mathrm{inc}}=\frac{2\pi }{\lambda }{n}_{{\rm{\sup }}}\,\sin ({\theta }_{{\rm{inc}}})\cos (\varphi )\). With θ inc fixed, the coupling of incident light to BSWs is realized by altering ϕ. Resonant generation of BSWs occurs when k x,inc = k BSW. Fig. 3 shows the surface mode coupling to BSWs as a function of azimuthal angle and wavelength for different values of superstrate refractive indices. This figure indicates directly how azimuthal angle sensing is achieved. For a fixed incident wavelength the azimuthal angle of coupling changes with superstrate refractive index. Similarly, at fixed azimuthal angle, the coupling wavelength alters with superstrate index.
The question of sensitivity of biosensors based on surface electromagnetic wave resonance - either surface plasmon polaritons48,49,50 or Bloch surface waves12, 13, 16, 17 - is an active research topic. For biosensing applications these sensors operate by detecting the change in dielectric loading at the surface of excitation due to reactions such as antibody-antigen binding of proteins or DNA-probe reactions13. However, because such reactions are widely variable, the use of sensitivity to index change of the analyte is used to compare different sensor designs. The Kretschmann and Otto prism configurations are the most widely used surface wave resonance sensors with angular sensitivity in the range of 50–100°/RIU and wavelength sensitivity (at 630 nm) in the range of 970 nm/RIU51. In general the grating coupling technique, although having an advantage of not requiring a voluminous prism, has suffered with lower sensitivity compared to prism coupling techniques.
However, all the studies on sensitivity analysis of grating coupling techniques have utilized only polar angle interrogation. Recently, Romanato et al.39 studied sensitivity enhancement in grating coupled surface plasmon resonance by azimuthal control. The authors search for an optimal value of the azimuthal angle, set to that value, and sweep over the polar θ inc angle. In this paper, we take an opposite approach. First the θ inc angle is set to an angle greater than θ BSW for ϕ = 0°, then the azimuthal angle is swept over to excite azimuthal BSW at appropriate ϕ.
Figure 4(a) shows BSW modes supported by the structure as a function of superstrate refractive indices and azimuthal angle for different values of polar incident angles at the wavelength of 632.8 nm. We observe that for high values of θ inc, the azimuthal angular range for BSWs get wider. More importantly, at smaller azimuthal angles, the dispersion curves tend to flatten, i.e., for a small change in the superstrate refractive index, the change in the azimuthal angle is signifantly larger. This behavior has a crucial impact in increasing the azimuthal sensitivity of BSWs. The azimuthal sensitivity \(({S}_{{n}_{{\rm{\sup }}},\varphi })\) is defined as
where, Δϕ is the change in the azimuthal angle and Δn sup is the change in the superstrate refractive index. The results for the azimuthal sensitivity given by Eqn. 9 are shown in Fig. 4(b). The sensitivity curves are computed from their respective colored BSW modes in Fig. 4(a). The improvement in the sensitivity can be clearly seen from the figure, with the azimuthal sensitivity as high as ~2500°/RIU. Higher sensitivity is especially useful for detecting tiny variations in the refractive index, as well as in detecting antibody-protein binding for disease detection. The sensitivity enhancement reported here is an order of magnitude higher compared to the previously reported grating coupled surface plasmon/BSW sensivities5, 52,53,54,55, which typically is in the range of 50–200°/RIU.
Figure 5(a) shows the reflectivity curves of the azimuthal BSWs for different values of the superstrate refractive indices. The solid curves are obtained using the 3D SMRCWA method, whereas the open circle curves are computed from COMSOL multiphysics. The results from both the numerical techniques are in excellent agreement with each other. We can observe from the figure that for a small change in the refractive index value \(({\rm{\Delta }}{n}_{{\rm{\sup }}}=0.005)\), the azimuthal angular shift between the resonance peaks get larger at small azimuthal angles. Finally, the field profile of azimuthal BSW for the superstrate refractive index of 1.33 (water) is shown in Fig. 5(b–d). The corresponding resonance peak is indicated in Fig. 5(a) by the arrows. As in the case of conventional BSW (ϕ = 0°), the surface field intensity is highly amplified, and the mode is slightly leaky as well.
(a) Reflectivity curves as a function of azimuthal angle for different values of n sup. The wavelength (λ) and incident angle (θ) are fixed at 632.8 nm and 5.4° respectively. The results obtained using COMSOL (circles) and an in-house 3D RCWA code (solid lines) show good agreement. (b) x-y (c) x-z (d) y-z plane views of azimuthal BSW at the resonance peak indicated by the arrows in (a).
Conclusion
In conclusion, we have studied a new way of exciting Bloch surface waves in dielectric multilayer structures with grating profile on the top-most layer via azimuthal interrogation. Fixing the polar incident angle to a value slighly higher than the BSW angle (for ϕ = 0° configuration), azimuthal BSWs can be excited by sweeping over the azimuthal angle. We show that as the refractive index of the superstrate layer increases, the azimuthal angular displacement between the BSW resonances increases as well. This change significantly increases the sensitivity of azimuthal BSWs. We report an order of magnitude higher sensitivity compared to the sensitivity of conventional BSWs.
References
Meade, R. D., Brommer, K. D., Rappe, A. M. & Joannopoulos, J. D. Electromagnetic Bloch waves at the surface of a photonic crystal. Phys. Rev. B 44, 10961 (1991).
Robertson, W. M. et al. Observation of surface photons on periodic dielectric arrays. Opt. Lett. 18, 528 (1993).
Robertson, W. M. & May, M. S. Surface electromagnetic wave excitation on one-dimensional photonic band-gap arrays. Appl. Phys. Lett. 74, 1800–1803 (1999).
Robertson, W. M. Experimental measurement of the effect of termination on surface electromagnetic waves in one-dimensional photonic bandgap arrays. J. Lightwave Tech. 54, 2013 (1999).
Rodriguez, R. G., Ryckman, J. D., Jiao, Y. & Weiss, S. M. A size selective porous silicon grating-coupled Bloch surface and sub-surface wave biosensor. Biosensors and Bioelectronics 53, 486–493 (2014).
Koju, V. & Robertson, W. M. Excitation of Bloch-like surface waves in quasi-crystals and aperiodic dielectric multilayers. Opt. Lett. 41(13), 2915–2918 (2016).
Liscidini, M. & Sipe, J. E. Enhancement of diffraction for biosensing application via Bloch surface waves. Appl. Phys. Lett. 91, 253125 (2007).
Liscidini, M. et al. Demonstration of diffraction enhancement via Bloch surface waves in a-SiN:H multilayers. Appl. Phys. Lett. 94, 043117 (2009).
Liscidini, M. & Sipe, J. E. Analysis of Bloch-surface-wave assisted diffraction-based biosensors. Virtual J. Biomed. Opt. 26, 279 (2009).
Delfan, A., Liscidini, M. & Sipe, J. E. Surface enhanced Raman scattering in the presence of multilayer dielectric structures. J. Opt. Soc. Am. B 29, 1863 (2012).
Pirotta, S. et al. Surface-enhanced Raman scattering in the presence of multilayer dielectric structures via Bloch surface waves. J. Phys. Chem. C 117, 6821 (2013).
Shinn, M. & Robertson, W. M. Surface plasmon-like sensor based on surface electromagnetic waves in a photonic band-gap material. Sensors and Actuators B 105, 360–364 (2005).
Farmer, A., Friedli, A. C., Wright, S. M. & Robertson, W. M. Biosensing using surface electromagnetic waves in photonic band gap multilayers. Sensors and Actuators B 173, 79–84 (2012).
Rizzo, R. et al. Optimization of angularly resolved Bloch surface wave bio-sensors. Opt. Exp. 22, 2566–2578 (2013).
Sinibaldi, A. et al. Direct comparison of the performance of Bloch surface wave and surface plasmon polariton sensors. Sensors and Actuators B 174, 292–298 (2012).
Giorgis., F., Descrovi, E., Summonte, C., Dominici, L. & Michelotti, F. Experimental determination of the sensitivity of Bloch surface waves based sensors. Opt. Exp. 18, 8087–8083 (2013).
Toma, K. et al. Bloch surface wave-enhanced fluorescence biosensor. Bio-sensors and Bioelectronics 43, 108–114 (2013).
Angelini, A. et al. Fluorescence diffraction assisted by Bloch surface waves on a one-dimensional photonic crystal. New Jour. of Phys. 15, 073002 (2013).
Frascella, F. et al. A fluorescent one-dimensional photonic crystal for label-free biosensing based on Bloch surface waves. Sensors 13, 2011–2022 (2013).
Frascella, F. et al. Enhanced fluorescence detection of miRNA-16 on a photonic crystal. Analyst 140, 5459–5463 (2015).
Soljačić, M. & Joannopoulos, J. D. Enhancement of nonlinear effects using photonic crystals. Nat. Mater. 3, 211–219 (2004).
Inoue, K., Oda, H., Ikeda, N. & Asakawa, K. Enhanced third-order nonlinear effects in slowlight photonic-crystal slab waveguides of line defect. Opt. Exp. 17, 7206–7216 (2009).
Kovalevich, T. et al. Opt. Express 25(5), 5710–5715 (2017).
Koju, V. & Robertson, W. M. Slow light by Bloch surface wave tunneling. Opt. Exp. 22, 15679 (2014).
Jamois, C., Li, C., Orobtchouk, R. & Benyattou, T. Slow Bloch surface wave devices on porous silicon for sensing applications. Phot. and Nano.-Fund. and Appli. B 8, 72–77 (2010).
Maradudin, A. A., Simonsen, I. & Zierau, W. Leaky surface electromagnetic waves on a high-index dielectric grating. Opt. Lett. 41(10), 2229–2232 (2016).
Hsu, C. W. et al. Bloch surface eigenstates within the radiation continuum. Light: Science & Applications 2, e84 (2013).
Hsu, C. et al. Observation of trapped light within the radiation continuum. Nature 499, 188–191 (2013).
Yoon, J. W., Song, H. S. & Magnusson, R. Critical field enhancement of asymptotic optical bound states in the continuum. Sci. Rep. 5, 18301 (2015).
Ding, Y. & Magnusson, R. Resonant leaky-mode spectral-band engineering. Opt. Express 12, 5661–5674 (2004).
Wang, S. S. & Magnusson, R. Theory and applications of guided-mode resonance filters. Appl. Optc. 32(14), 2602–2613 (1993).
Magnusson, R., Yoon, J. & Wawro, D. Properties of resonant modal-plasmonic multiparametric biosensors. Proc. SPIE. Frontiers in Biological Detection: From Nonosensors to Systems V 8570, 85700K, doi:10.1117/12.2004550 (2013).
Fattal, D., Li, J., Peng, Z., Fiorentino, M. & Beausoleil, R. G. Flat dielectric grating reflectors with focusing abilities. Nat. Photon. 4, 466–470 (2010).
Lee, J. H. et al. A semiconductor metasurface with multiple functionalities: A polarizing beam splitter with simultaneous focusing ability. Appl. Phys. Lett. 104, 233505 (2014).
Ginn, J. C. et al. Realizing optical magnetism from dielectric metamaterials. Phys. Rev. Lett. 108, 097402 (2012).
Monticone, F. & Alù, A. Leaky-wave theory, techniques, and applications: from microwaves to visible frequencies. Proc. IEEE 103(5), 793–821 (2015).
Collin, S. Nonostructure arrays in free-space: optical properties and applications. Rep. Prog. Phys. 77, 126402 (2014).
Kim, D. Y. Effect of the azimuthal orientation on the performance of grating-coupled surface-plasmon resonance biosensors. Appl. Opt. 44(6), 3218–3223 (2005).
Romanato, R., Lee, K. H., Kang, H. K., Ruffato, G. & Wong, C. C. Sensitivity enhancement in grating coupled surface plasmon resonance by azimuthal control. Opt. Exp. 17(14), 12145–12154 (2009).
Elston, S. J., Bryan-Brown, G. P. & Sambles, J. R. Polarization conversion from diffraction gratings. Phys. Rev. B 44, 6393 (1991).
Passilly, N. et al. Polarization conversion by dielectric subwavelength gratings in conical mounting. J. Euro. Opt. Soc. 3, 08009 (2008).
Laroche, M., Marquier, F., Vandenbem, C. & Greffet, J. Polarization conversion with a photonic crystal slab. J. Euro. Opt. Soc. 3, 08038 (2008).
Devore, J. R. Refractive indices of Rutile and Sphalerite. J. Opt. Soc. Am. 41, 416 (1951).
Malitson, I. H. Interspecimen comparison of the refractive index of Fused Silica. J. Opt. Soc. Am. 55, 1205 (1965).
Kim, S. Y. Simultaneous determination of refractive index, extinction coefficient, and void distribution of titanium dioxide thin film by optical methods. Applied Optics 35(34), 6703–6707 (1996).
Joannopoulos, J. D., Johnson, S. D., Winn, J. N. & Meade, R. D. Photonic crystals: Molding the Flow of Light (Princeton University Press, 2008).
Koev, S. T., Agrawal, A., Lezec, H. J. & Aksyuk, V. A. An efficient large-area grating coupler for suface plasmon polaritons. Plasmonics 7, 269 (2012).
Matsubara, K., Kawata, S. & Minami, S. Optical chemical sensor based on surface plasmon measurement. Appl. Opt. 27, 1160 (1988).
Zhang, L. M. & Uttamchandani, D. Optical chemical sensing employing surface plasmon resonance. Electron. Lett. 23, 1469 (1988).
Vukusic, P. S., Bryan-Brown, G. P. & Sambles, J. R. Surface plasmon resonance on grating as novel means for gas sensing. Sensors and Actuators B 8, 155 (1992).
Homola, J., Yee, S. S. & Gauglitz, G. Surface plasmon resonance sensors: review. Sensors and Actuators B 54, 3–15 (1999).
Byun, K. M., Kim, S. J. & Kim, D. Grating-coupled transmission-type surface plasmon resonance sensors based on dielectric and metallic gratings. Appl. Opt. 46(23), 5703 (2007).
Hu, C. & Liu, D. High-performance grating coupled surface plasmon resonance sensor based on Al-Au bimetallic layer. Mod. Appl. Sci. 4(6), 8 (2010).
Kadomina, E. A., Bezus, E. A. & Doskolovich, L. L. Diffraction-grating-based Bloch surface wave refractive index sensors. Comp. Opt. and Nanophotonics, Information Technology and Nanotechnology (ITNT-2016).
Kang, X., Wen, L. & Wang, Z. Design of guided Bloch surface wave resonance bio-sensors with high sensitivity. Opt. Comm. 383, 531 (2017).
Author information
Authors and Affiliations
Contributions
V.K. and W.M.R. conceived the project and V.K. performed numerical simulations. V.K. and W.M.R. both wrote and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Koju, V., Robertson, W.M. Leaky Bloch-like surface waves in the radiation-continuum for sensitivity enhanced biosensors via azimuthal interrogation. Sci Rep 7, 3233 (2017). https://doi.org/10.1038/s41598-017-03515-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-03515-0
This article is cited by
-
Highly sensitive refractive index sensor based on Bloch surface waves with lithium niobate film
Applied Physics A (2022)
-
Novel Bloch wave excitation platform based on few-layer photonic crystal deposited on D-shaped optical fiber
Scientific Reports (2021)
-
Correcting the formalism governing Bloch Surface Waves excited by 3D Gaussian beams
Communications Physics (2020)
-
Two-Dimensional Hole-Array Grating-Coupling-Based Excitation of Bloch Surface Waves for Highly Sensitive Biosensing
Nanoscale Research Letters (2019)
-
Inverse photonic design of functional elements that focus Bloch surface waves
Light: Science & Applications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.