Abstract
DNA shape is emerging as an important determinant of transcription factor binding beyond just the DNA sequence. The only tool for large scale DNA shape estimates, DNAshape was derived from Monte-Carlo simulations and predicts four broad and static DNA shape features, Propeller twist, Helical twist, Minor groove width and Roll. The contributions of other shape features e.g. Shift, Slide and Opening cannot be evaluated using DNAshape. Here, we report a novel method DynaSeq, which predicts molecular dynamics-derived ensembles of a more exhaustive set of DNA shape features. We compared the DNAshape and DynaSeq predictions for the common features and applied both to predict the genome-wide binding sites of 1312 TFs available from protein interaction quantification (PIQ) data. The results indicate a good agreement between the two methods for the common shape features and point to advantages in using DynaSeq. Predictive models employing ensembles from individual conformational parameters revealed that base-pair opening - known to be important in strand separation - was the best predictor of transcription factor-binding sites (TFBS) followed by features employed by DNAshape. Of note, TFBS could be predicted not only from the features at the target motif sites, but also from those as far as 200 nucleotides away from the motif.
Similar content being viewed by others
Introduction
The physical basis of protein-DNA interactions has been explained from the perspective of direct recognition of nucleic acid bases by complementary TF residues or through an indirect recognition of sequence-dependent DNA structure, more appropriately termed as base and shape readout respectively in the recent literature1,2,3,4. While the former ignores the differential accessibilities of DNA bases in the double helix, the latter assumes the existence of a unique and exclusive structure of the DNA. Base readout having been the primary focus of investigations, numerous methods to model sequence features of TF binding sites as a consensus motif or position weight matrices (PWMs) have been successfully developed5,6,7,8,9. However, the number of studies focusing on DNA shape or conformational dynamics has been limited2, 3, 10,11,12,13. Part of the problem is the lack of tools to rapidly estimate the DNA conformation or its dynamics directly from the sequence. The DNA shape prediction tool, “DNAshape” provided a major innovation in the computational determination of DNA shape and allowed genome-scale study of the contribution of DNA shape to TF binding site recognition2. Trained on Monte Carlo simulation data, DNAshape takes a nucleic acid sequence as its input and predicts four sequence-dependent shape features. It uses a five-nucleotide window (for the base-pair features) and a six-nucleotide window for the base-step features and can be thought of as a dictionary to translate an exhaustive set of small DNA fragments into their corresponding shape features. Use of the four features, predicted by DNAshape has resulted in highly accurate classifiers to distinguish between TF binding and non-binding DNA sequences e.g. in explaining the data from the DREAM5 competition for predicting TF binding specificities14. Despite these successful implementations and substantial evidence that DNA shape encoded in the sequences is critical for TF recognition, the body of work available on the subject is limited compared to sequence-only analyses. For example, most of the TF target search methods such as Transfac or Uniprobe have not yet implemented a shape based analysis15, 16. Even in the studies employing DNA shape, the focus has been limited to a relatively small number of shape features. It may be intuitive that a simpler model, utilizing fewer features is easier to interpret, but we believe it may not necessarily reflect the entire picture of TF-target recognition. Consequently, it is helpful to explore more shape features and hence verify both the completeness and competitiveness of DNAshape. For this purpose, predictive models for much larger set of DNA shape features need to be developed.
We have previously developed techniques to thread DNA sequences onto the structure of a known protein-DNA complex and to determine the energy of cognate and designed sets of sequences17,18,19,20,21,22,23. This approach was based on developing a statistical force field from the observed co-variances in 12 DNA shape features. Trained force field features could estimate the intrinsic sequence energies for a given DNA shape and thereby return the specificities of sequence-dependent structures. Using a combination of base readout energies and those predicted from our statistical force fields, we successfully explained the specificities of the observed DNA sequences in the known protein-DNA complexes. Realizing the inadequacies of the data taken from the crystal structures of protein-DNA complexes, we have also employed molecular dynamics (MD) derived shape data to make more accurate estimates of force field parameters20. Separately, we have tried to explore and predict the sequence-dependence of DNA solvent accessibility by analyzing their structures available from the Protein Data Bank (PDB)24. However, in most of these works, we focused on shape specificity in terms of sequence-structure relationships and the shape dynamics itself was not incorporated into the predictive models. Moreover, our evaluation of sequence specificities was focused on high-resolution structures of protein-DNA complexes and not on the genome-wide TF-target associations.
Here, we present a novel approach, called DynaSeq to model DNA sequence specificities using MD-derived sequence-dependent conformational ensembles, instead of their static values. We define and predict an ensemble each for an exhaustive set of 13 shape features or conformational parameters, of which 12 (Shift, Slide, Roll, Buckle, Helical Twist, Propeller Twist, Stagger, Shear, Tilt, Rise, Stretch and Opening) completely describe its atomic structure, and the 13th (Minor Groove Width; MGW) is used to draw comparisons with DNAshape features25. DynaSeq is a set of support vector regression models (SVRs), trained to predict conformational ensemble occupancies at different nucleotide positions in a given sequence environment. Ensemble definitions are obtained from a data pool of MD simulation snapshots for 136 unique tetrameric DNA sequences and ensemble occupancies are obtained at each base position in each sequence independently. Subsequently trained models are capable of predicting ensemble occupancies for any nucleotide-sequence in much the same way as DNAshape but for a much larger feature set. Upon comparison between DNAshape features and the corresponding values derived from DynaSeq, we observe a good agreement in the predicted values for the common feature sets. Yet the latter allowed us to investigate the predictability of TFBS from other shape features both as ensembles of single individual parameters as well as a single superset of them all.
For a large scale assessment of the power of the different feature sets of DynaSeq (and for comparison, DNAshape) to predict TFBS, we utilized the available data set of TFBS for a large number (1312) of TFs identified by the Protein Interaction Quantification (PIQ) algorithm under similar conditions for the same cell type (mouse embryonic stem cells; mESCs)26. Developing predictors employing ensemble occupancies of one (out of 13) shape feature at a time we assessed the ability of individual conformational parameters to model TFBS. Results indicated that “base pair opening” was the most powerful predictor in majority of the cases followed by some of the features currently employed in DNAshape. For models employing a large feature set of all ensemble occupancies of all parameters, D ynaSeq successfully explained the observed genome-wide binding data with high accuracy. Thus, our results suggest that the performance of DynaSeq is comparable to and arguably better than the similar models built on DNAshape features. Both DNAshape and DynaSeq based models revealed that in most cases, TFBS could be predicted not only from the shape of the target motifs but also from the flanking regions as far as 200 bases away in a 5′ or a 3′ direction.
Taken together, this study provides a novel approach to study DNA structural dynamics at a genomic scale and indicates that information about TF-DNA binding is contained not only in the exact site of TF-binding but also extends to much larger flanking region of DNA. The dictionary of the current implementation of DynaSeq can be accessed from http://dynaseq.sciwhylab.org.
Results
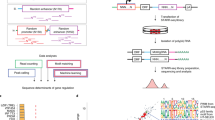
The overall design of the study is shown in Fig. 1. As shown, the study consists of three components viz. (1) Defining and generating a conformational ensemble for an exhaustive set of tetrameric DNA sequences flanked by a GCGC tetramer on both 3′ and 5′ terminals. (2) Developing and benchmarking DynaSeq as a sequence-based tool for predicting shape ensemble occupancies of nucleotides in different sequence environments and finally (3) Applying DynaSeq to predict genome-wide binding sites for 1312 TFs and identifying the most predictive shape feature in each of them. Results obtained from these analyses are presented below.
Overall design of the present study. The study consisted of three steps. (a) Molecular dynamics (MD) simulations were performed for all the unique tetramers flanked by a fixed tetramer on both terminals and the conformational trajectory of the central four nucleotides was converted into a conformational ensemble by defining equal frequency ensemble bins from the entire data. (b) A set of 65 SVR models were trained, one each for the five ensemble bins of the 13 conformational parameters. Models could then use a nucleotide sequence as the input and predict 65 features (representing ensemble bin occupancies) of a nucleotide in the corresponding sequence environment. A number of benchmarks for the effectiveness of DynaSeq were performed. These included the models’ performance in recalling PDB deposited structures (using predicted occupancy-weighted averages of ensemble bins) and DREAM5 TF specificities (from the ensemble occupancies for a sequence window). (c) Benchmarks on DynaSeq’s ability to classify TFBS from genomic controls were performed. Predictors were trained by pooling all the 65 features together and also by using just a 5-bin ensemble of a single conformational parameter at a time as the sequence feature.
Global conformational ensemble
DynaSeq consists of 65 SVR models trained on Molecular dynamic (MD) simulation data of 136 tetranucleotides, represented by five ensemble bins for each of the 13 helical/step conformational features for each base of the DNA sequence. The observed values of conformational features from the pooled poses of MD trajectories (544 × 105 values) have been used to define five equal probability bins. The exact ranges or bin boundaries, are shown in Supplementary Figure SF1(a). By definition each bin is expected to have an equal (20%) occupancy, in the global ensembles. However, individual bases and their sequence neighbors, specifically alter these globally deduced values, quantifying the sequence-dependent DNA shape dynamics. General variations in the occupancies across individual ensembles in the MD data (corresponding to various bases under different environments) are plotted in the form of their standard deviations in Supplementary Figure SF1(b). At the first level of specificity, each of the four bases (pooling together all occurrences of the corresponding base irrespective of their flanking bases) has a unique ensemble profile as shown in Supplementary Figure SF1(c). Explicit interpretation of this profile is not possible, but the existence of specific variations, which may play a role in recognizing unknown complementary TF structures, can be noted. For example, the first bin of shear is depleted in the case of Adenine and Cytosine and enriched for Guanine and Thymine. On the other hand both of the triple-hydrogen bond forming bases, Guanine and Cytosine, have an enriched first bin for stretch, which is opposite to what we observe for Adenine and Thymine. Subtle variations are also observed for other conformational features. In addition to the base-wise variations, sequence neighbors also specifically alter these conformational ensembles, leading to the sequence-dependent DNA conformational dynamics (for reference, specificities caused by a single base neighbor for all 64 possible combinations are shown in Supplementary Figure SF1(d)). Modulation of ensemble bin occupancies by neighboring nucleic acid bases forms the basis of DynaSeq. Conceptually, this is similar to the sequence-dependent shape features in DNAshape. However, the origin of reference data, scope and the content of the two tools are different as outlined above.
DynaSeq: Sequence to ensemble predictor
Cross-validation and prediction performance
To develop DynaSeq and evaluate its power to predict shape ensembles defined from our MD trajectory data, we created independent training and test data sets in a leave-one-out fashion; trained the ensemble occupancies for all base positions in 135 DNA sequences and tested the predictive power for the left-out 136th. Results from an exhaustive set of 136 combinations were pooled and evaluated.
Each of the 65 SVR models in DynaSeq, takes identities (A, C, G or T) of a DNA base and its sequence neighbors within a defined window as inputs and is trained to return the corresponding ensemble bin occupancies as the output. The whole set of 65 occupancy values returned from the models is also referred to as predicted ensemble in the manuscript. Figure 2 summarizes the prediction performance of cross-validated SVR models. We trained and tested various window spans and found that a 5-nucleotide window is optimum for the prediction models on the current data. Based on this optimized model, most of the ensemble bin occupancies are predicted well (~80% with an absolute error of 5 percentage points (Fig. 2b)). A high correlation (R = 0.94) between the predicted and observed values in the entire population range further indicates the stability of the prediction model (Fig. 2c). Furthermore Fig. 2(c) and (d) indicate that the populations, highly skewed from their global 20% average value, are also estimated well, albeit with a slightly higher error rate for the first and last bins than for the values in the middle. However, the worst-case Mean Absolute Error (MAE) is still less than 6% (observed in the first bin of slide).
Cross-validation and predictability of DNA conformational ensemble occupancy at each base position. (a) Variation of mean absolute error (absolute difference between prediction and observed ensemble occupancy in each bin) with training window sizes. Standard deviation in the overall data is shown in red, whereas other values represent cross-validation performances. (b) Overall cumulative frequency of absolute error distribution at window size = 5. Prediction for each base in any position of a tetranucleotide is counted once and errors computed are for the left out sets in leave-one-tetranucleotide cross-validations. (c) Scatterplot of predicted versus observed occupancies in all bins and all conformational parameters (d) Mean absolute error averages for each bin occupancy.
Cross-validation results provided above indicate the robustness of the predictions of sequence-dependent ensembles across 136 independently generated MD trajectories on different unique tetramers. To further evaluate the power of DynaSeq models critically, we performed additional benchmarks as described below.
Comparison with DNAshape on the common descriptors
We have used 3DNA25 a widely popular DNA structural analysis tool to describe DNA shape features. 3DNA generates two types of conformational features from the atomic coordinates of a DNA structure: the deformations in complementary bases, also called base-pair features and the deformation with respect to the stacking of base pairs along the helical axis, also called the base-step features. DNAshape assigns base-step and base-pair parameters to a pair of bases and an individual base respectively, which is technically appropriate but causes an offset between the two sets of values. To describe a DNA sequence and corresponding shape more uniformly, in DynaSeq, we assigned both the base-pair and base-step parameter to a single base position as described in supplementary methods. Thus DynaSeq global dictionary for the finally selected 5-base window consists of 45 values, whereas the number is 46 for DNAshape.
Further, DynaSeq models DNA dynamics instead of its static structures and therefore a comparison with DNAshape was made after converting the DynaSeq-predicted ensembles to their averaged shape feature values (see Methods).
Having addressed the issues described above, we computed DNAshape and DynaSeq features for all the possible 6-mers (46 = combination; with third base position in DynaSeq corresponding to 4th in DNAshape for the base-step parameters) and evaluated the agreement between DynaSeq-derived equilibrium values and the corresponding DNAshape predictions (Fig. 3). We observed a good correlation between the predicted values by the two methods with Pearson’s correlation ranging from 0.61 to 0.73 (Fig. 3(a)). We also observed that several conformational features in DynaSeq are not well correlated with any of the four DNAshape features, thereby suggesting that DynaSeq provides more clues about the DNA conformations than DNAshape (Fig. 3(b)). However, at the outset it is unclear whether this information, even though different from DNAshape is actually useful for modeling transcription factor specificities or otherwise. In the following sections, we present results that highlight what DynaSeq could achieve that DNAshape could not.
Agreement between DNAshape and DynaSeq features. The four conformational features provided by DNAshape have also been predicted using DynaSeq (occupancy-weighted average of ensemble bins). All the four features show strong correlation, supporting the evidence of sequence-dependent specificity in DNA structures. (a) Detailed scatterplot of each of the overlapping features. Even though, there is an implicit offset between the MGW values reported in DNAshape and DynaSeq (due to the use of different definitions and software to compute MGW), the general agreement observed through Pearson’s correlation remains strong. (b) Comparison between the 12 DynaSeq features and their mutual correlation with the four DNAshape features shows that several of the 12 parameters (e.g. shift and tilt) are significantly novel as they show no correlation with any of the DNAshape features.
Evaluating sequence-specificity of known three-dimensional DNA-structures
DNAshape predicts only four shape features, which are not adequate to model complete DNA structures in atomic details. On the other hand DynaSeq is capable of predicting all the parameters required for rebuilding complete three-dimensional structures for DNA and could therefore be useful in docking and other problems of protein-DNA complex design. We evaluated whether the DynaSeq-predicted structures of DNA sequences in the protein data banks (PDB) are any closer to the reported structures compared to those predicted for a set of randomly generated sequences of the same length. To avoid, confounding factors from other proteins, we used only the free DNA structures for this purpose. The results indicate that the known DNA structures could be favorably recalled from their predicted ensembles using only the DNA sequence with an RMSD (root-mean square deviation) of 4.2 Å compared to 7.5 Å for the randomly generated sequences (Z-score = −1.48) (summary in Table 1; Detailed results in Supplementary Table ST1). These results provide promise for DynaSeq’s ability to help in more accurate design and modeling of protein-DNA complexes27.
DynaSeq’s ability to predict TF specificities for DREAM5 data sets
Dialogue for Reverse Engineering Assessments and Methods (DREAM) is a series of crowdsourcing challenges to solve biological and medical problems28. The fifth of this series of challenges, DREAM5 consisted of a competition to predict TF binding specificities for an exhaustive list of fixed length DNA sequences in a hold-out blind prediction manner14. Results of one binding assay were made available to train models and the predictions on a similar assay were tested in a blind experiment. Even though the training and test data sets are somewhat redundant in the two cases, it would be interesting to note how well DynaSeq could have performed by doing a retrospective analysis. DynaSeq provided highly accurate recall of TF specificities on DREAM5 data sets trained in the manner similar to the conditions of the competition (Supplementary Methods and Supplementary Figure SF2). Prediction was evaluated by AUC (area under the curve) of a receiver operating characteristic curve (i.e. true positive rate plotted against false positive rate), which is used in optimal model selection.
When using the common features in DNAshape and DynaSeq, AUC results agreed with each other (Figure SF2(a)). When a consensus was taken between results obtained by DNAshape and DynaSeq models, the AUC shows significant improvement over DNAshape-only results with a mean AUC rising from 75.68% to 77.60% (p-value from a paired Student’s t-test = 0.0015) (Figure SF2(b)). Finally, when all the 65 features were used in the prediction model, DynaSeq outperformed DNAshape by raising the average AUC to 93% (a gain of 18% AUC) (Figure SF2(c)). In particular, DynaSeq with the full set of features improved lower AUCs yielded by DNAshape (Figure SF2(d)). Some of this improvement could be caused because of high redundancy in DREAM5 experiments and larger number of features in DynaSeq compared to DNAshape. Even so, in terms of the conditions set out in DREAM5, the proposed DynaSeq approach had a clear advantage over DNAshape and at the very least provides an alternative route to perform DNA shape analysis at a large scale.
It should be noted that, while this work was being prepared for submission, another study using DREAM5 data for benchmarking DNAshape performance in identifying TFBS was reported29. However, that work corresponds to a different perspective, demonstrating how k-mer information could be combined with shape features and the detailed results about AUC, we employed here are not available. Our focus in the above has been how DNAshape and DynaSeq predicted features produce similar or different levels of TFBS specificity predictions.
Predictability of TFBS from DynaSeq features in a sliding window
We next set out to evaluate DynaSeq’s performance in predicting TFBS using a sliding window on and around the sequence motifs. For this purpose we used the recently reported binding site information for a comprehensive list of TFs identified by a computational algorithm (Protein Interaction Quantitation or PIQ) using DNase-Seq data30. A number of attributes of this database make it a good choice to evaluate and compare TF binding site prediction methods. First, the database reports the binding sites of a large number of TFs (1,312). Secondly, binding sites are assigned based on the experimental chromatin accessibility data (DNase-Seq) followed by PWM-based motif assignment, thereby ensuring that the annotated regions are indeed the binding sites of a given TF (and not its co-factor, as could be the case in a ChIP-Seq experiment). Thirdly, genome-wide binding and control data come from identical cellular and processing conditions. We evaluated the ability of DynaSeq-predicted ensembles to classify TFBS from genomic controls by creating sequence windows at different positions with respect to the motif start position and using their conformational ensembles to create cross-validated classifiers.
We placed a sliding window covering a fixed number of nucleotides at different distances from the motif start positions (motif start site is defined as per the PIQ annotations) and trained an elastic-net regularized logistic regression model to classify binding sites from non-binding sites (see Methods) using 10-fold cross validation. All the binding sites of a TF and the control regions are collected individually and prediction models are trained for each pair of binding and control regions of the TF. The AUC of ROC for a classifier in this 10-fold cross-validated predictive modeling is used to evaluate the performance of DynaSeq features to predict TFBS compared to DNAshape features. AUC is determined at all positions for all TFs individually and the entire set of 1312 values is averaged to estimate the performance levels across all TFs.
Prediction models were developed in two ways to draw an unbiased comparison. First, predicted ensemble bin occupancies for only one conformational feature was used and 13 cycles of such predictions were made to assess which of the 13 parameters had the most accurate predictions. Secondly, all the ensembles from all of the 13 parameters were put together to create an all-feature model, primarily to compare it with models trained with the smaller number of static features from DNAshape.
TFBS predictions from single parameter ensembles
We examined the performance of each feature by feeding ensembles of only one shape parameter into TFBS prediction models. We observed that even though the ensembles of all the 13 parameters considered here lead to comparable performance levels (Fig. 4a,b), two of the four parameters, Roll and Prop-Tw used in DNAshape are among the top five (Fig. 4d). This validates the choice of the parameters in DNAshape and highlights the critical nature of these shape properties. Surprisingly, however, the top ranked feature in our analysis was “base-pair opening”, a feature not used by DNAshape. It is intuitive to think that base-pair opening may represent the DNA base accessibility better than other shape parameters (Supplementary Table ST1). Although detailed experiments will be needed to determine the physical effect of base-pair opening on TFBS, its ability to predict TFBS better than any other single conformational parameter is a surprising outcome of our analysis. It is possible that base-pair opening is indeed a critical mechanism of strand separation required for TF binding as argued in earlier works31.
Ability of single parameter conformational ensembles to predict TFBS in PIQ data. (a) TFBS’s were classified from genomic control positions using 65 ensemble features at motif site and its +/−200-nt distance using 7-nt window at each position in each of the 1312 TFs and distribution of AUC for all such predictions was represented in a boxplot. (b) The data were separated for motif positions (0 to 15 bases from motif start) and (c) outside of it. Results in (a–c) indicated that “opening” ensemble is the best predictor of TFBS in both regions (even if the difference between AUC is small), followed by parameters whose static values are also used in DNAshape (see (d)) (d) Relative number of times a conformational parameter appeared in the top-ranked position in all positions in all TFs was counted.
From the perspective of accurate prediction of binding sites, it is evident that DynaSeq can provide an alternative approach for modeling of genome-wide TFBS.
Comprehensive modeling of genome-wide binding sites in 1312 TFs
To further evaluate how DynaSeq-derived shape ensembles can model TFBS dynamics, we created their predictive models from an exhaustive set of features in our models. Figure 5 shows the comparison between prediction models trained using four DNAshape features versus those which employ all the 65 bin occupancies used by DynaSeq for a range of window sizes. Cross-validation and regularization in the elastic net attempts to ensure that the models are not over-fitted for DynaSeq (See Supplementary Methods SM2).
Comparison between DNAshape and DynaSeq implementations to discriminate TFBS from genome-wide controls. Different sliding windows are placed at the motif start positions and performance levels are scanned +/−200 bases away from motif sites assigned by PIQ. AUC results are computed on 1312 TFs in PIQ data and averaged to produce these plots to have a comprehensive global view. Performance of DynaSeq is comparable with DNAshape in most cases and seems to be slightly better for smaller window sizes but difference in performances of DNAshape and DynaSeq diminishes at large window sizes because of strict cross-validation which penalizes models with higher number of features.
We observe that DynaSeq could more accurately distinguish binding sites from control as compared to DNAshape at the motif position as well as its flanking regions, especially for smaller sliding windows. However, at large window sizes, difference in DNAshape and DynaSeq performances starts to disappear, presumably because of the use of a strict cross-validation and elastic net regularization, both of which penalize models using more features. This is supported by the fact that AUC values for neither DNAshape, nor DynaSeq based models increase significantly beyond this point. More work would be needed to enable utilization of very large sequence windows for modeling TFBS using DynaSeq, although encouragingly DynaSeq performs at the same level as DNAshape for a window size of 7 nucleotides or smaller. This window size is used for evaluating contributions from an exhaustive set of conformational parameters only few of which are covered in DNAshape. Recently, another study also addressed the analysis of the DREAM5 by employing DNAshape, they also reported that the models combining k-mers with DNA shape are more successful at smaller windows, presumably due to the arguments we present above29.
With a window size of 7 nucleotides, even though on average the performance levels appear similar, there is still a statistically significant difference in favor of DynaSeq in comparison to DNAshape. While for reasons discussed above this difference does not hold for larger window sizes, the TF-wise scatterplot of performances (Fig. 6(b)) shows that the general trends are very similar across various TFs. However, 91 TFs show improved performance of more than 5% AUC with DynaSeq compared to DNAshape, whereas only 12 of them showed the opposite trend. The identities of the two TFs groups are presented in Table 2. A quick look suggests that many of the TFs whose binding sites are better predicted by DynaSeq are minor groove binders such as TATA box binding and those known for causing large scale DNA bending in their targets. A comprehensive analysis of their functional implications is being carried out and will be reported separately.
Performance evaluation of DynaSeq for individual TFs and in comparison to DNAshape and GC content based models for a 7-nt window. (a) Each TF is represented by a single AUC, which is the highest value from the 401 AUC values computed at each of the +/−200 nt positions from the motif start position of that TF. (b) Correlation between the best AUC values by DynaSeq and those by DNAshape. (c) A single cumulative performance level is obtained by averaging AUCs of all TFs at each of the 401 positions relative to their motif start site and shows how the perfomance levels vary when DNAshape and DynaSeq features from these positios are used in predictive models. However, such changes are not observed when GC content used. (d) AUC values plotted as a function of distance from motif. The values were calculated using data of Fig. 6(c). The plot gives a directionless estimate of predictability of TFBs from non-motif positions.
A comparison with GC-content based predictions
Some shape features such as propeller-twist and opening have been reported to be highly related with GC-content30,31,32. One wonders if some of the predictive ability in the above models is caused by the GC-content of the binding sites. To address this question, we trained models to predict TFBS using GC content in a 7-nt window for all the considered positions similar to DNAshape and DynaSeq. Figure 6(c,d) shows the results obtained by DynaSeq, DNAshape and GC-content in the same plot both in terms of the absolute and signed distances from the motif sites. It is clear that at, and even as far as 200 bases from the motif location, the shape-based models carry significantly more information than the GC-content alone. Thus, we conclude that the analysis based on shape and dynamics in this work goes beyond the standard considerations of compositional biases in genomic TF targets. This holds true not only for the composite models with integrated feature sets but also for those based on single conformational parameters as in section 2.3.1 as the latter shows an AUC close to 60%, which is about 5% better than the GC-content based model shown in Fig. 6(c,d).
Discussion
DNA conformational dynamics is known to play a crucial role in its recognition by proteins. Several approaches to model it from sequence have been developed resulting in increasingly deeper insights33,34,35,36,37,38,39. The only method for genome-wide prediction of DNA shape available in public domain provides its estimates in terms of static values, which cannot directly capture significant DNA properties such as sequence-dependent polymorphism38, 39. In this work, we have shown how the static equilibrium values of DNAshape parameters may be augmented with the introduction of a shape ensemble instead of shape parameter values. Further, we include additional parameters that enable modeling the complete atomic structure of DNA for a give sequence.
The exact nature of conformational dynamics in TF recruitment, target search and complex stabilization is not well understood even though the role of binding site proximal and contiguous regions at genomic scales has been recently reported40. This study provides support for the results reported in ref. 40 from a different perspective and goes on to look at a more comprehensive description of structure. Conformational dynamics of TFs’ genomic targets has been elusive partly due to the lack of methods to perform large-scale simulations. In this work, we attempt to bridge this gap and show that predicted conformational dynamics provide important biological insights into TF recognition of its genomic targets.
TFs in general show highly redundant sequence-specific DNA binding41, yet they can exhibit highly specific cell-type activity42. Here we show that DNA regions much larger than the well-known TF binding sequence motifs encode shape and specificity information for TFs, indicating that genomic DNA is not just a ‘passive observer’ of TF binding. Instead, TF-DNA interaction is a mutual event between the DNA sequence and the TF, which acts in unison to bring about specific biological activity, as highlighted earlier43. This also reiterates the significance of allostery and cooperativity in protein-DNA recognition as implied from our previous works44,45,46,47. The allosteric effect in DNA targets in the recognition process is a subject of great interest 44,45,46, 48,49,50,51. An analysis at a scale done in this work is not available and our results suggest a role for allosteric control in target recognition of most TF targets.
In this work, we present a novel approach to predict sequence-dependent DNA-conformational ensembles directly from sequences, which does not require detailed simulations of their structures. Models were trained and cross-validated on MD simulations of all unique tetrameric DNA sequences and perform well in various evaluation tests. Model systems representing genome-wide binding preferences of TFs were analyzed. Genome-wide binding preferences of 1312 TFs could be modeled using features derived from predicted conformational ensembles. Together, these results suggest the cooperation of much larger chromatin regions and potential modularity between them for many TF-target associations than realized so far.
Base-pair opening is a fundamental molecular process in strand separation which is essential in transcription, DNA replication and recombination52. It has been suggested that negative supercoiling of DNA or intermolecular DNA-DNA interactions33 induces the strand separation. Thermal fluctuations leading to base-pair opening, also called DNA breathing are known to be sequence-dependent53, which seems to be well-represented by our conformational ensemble. In this study, we found that the base-pair opening feature contributed the most in predicting TFBS, indicating that the energy barrier in the strand separation is lower at TFBS as well as within the 200 upstream and downstream of TFBS. The genomic positions where the strand separation should occur might actually be encoded in the DNA-sequence itself, so that transcription can smoothly start.
In summary, this work presented a novel approach to predict DNA shape in the form of a conformational ensemble and depicted its practical applicability in modeling large scale TFBS data from multiple sources. In particular, the role of DNA shape in protein-DNA interactions is vindicated and a step in understanding them better is made possible.
Methods
The detailed methods for each one of the three components of this study as outlined in Fig. 1 are explained in the following.
MD trajectory to conformational ensemble
Molecular Dynamic (MD) simulation of 12-mers
DynaSeq predictions are based on conformational ensembles obtained by molecular dynamics (MD) simulations. MD simulations were performed for 100 ns on each of the 136 unique (12 mer) DNA sequences with an explicit solvent model. Each of these 12 mers has a unique tetrameric DNA sequences at the center and flanked by GCGC on terminal positions. The detailed simulation conditions in this study were the same as described in our previous work18. This method of collecting MD trajectory data to analyze sequence-dependent effects is consistent with our previously reported works18, 54 and one by the ABC project55. The latter has grown in size and scope over a period of time, but due to practical reasons of data accessibility we retained our method, which has been shown to produce sound scientific insights into sequence-dependent DNA dynamics.
However, as an advance over our previous works, in the current study, we have opted for bsc0 force field to describe nucleic acid atomic interactions56 (After this study was completed, another version of this force field parambsc1 57 was released, which addresses some of the limitations observed in bsc0. Since the approach presented here is based on a high degree of coarse-graining of ensemble populations, we do not expect a dramatic change by using the new version. Notwithstanding, we plan on detailed comparisons that will be reported in the future.) Snapshots were saved every 1 ps (500 steps), yielding 100,000 snapshots for each tetrameric sequence.
Computation of conformational features of all poses in central tetramers
From the snapshots obtained above, 13 conformational features at each base position in the central tetramer were computed, leading to 136 × 4 = 544 sets of 13 such values each from a snapshot. A list of 12 of these features (Supplementary Table ST1) and their definitions is provided in Supplementary Materials, while the minor groove width (MGW) forms the 13th feature (not shown in the table). Conformational feature values were computed using a local installation of the 3DNA program25. Both base pair helical and base pair step parameters are adopted from the bp_step.par file generated by the “analyze module” of 3DNA program. As per the convention of this software, base step parameters between the i-1 th and i th positions are assigned to the i th position in a nucleotide sequence.
Definition of global conformational ensemble using 5 equal-frequency bins
Each of the 13 conformational features from the snapshots were pooled together to define five equal frequency bins. Conformational feature values were split into five ranges using four break points such that each range was occupied by 20% of the snapshots or poses from all base positions (Figure SF1(a)). For example, all values of twist were pooled together from all positions of all tetramers and sorted in ascending order. Between the extreme observed values and four break points are defined to create five bins, each of which is expected to have 20% poses in a global data. These ranges were termed as global ensemble bins. These occupancies differ from the 20% when data from only specific positions are considered, as seen in (Figure SF1(b–d)). This specificity of different base environments needs to be captured by a training model and forms the basis of most analyses in this work.
Mapping MD trajectory data of all nucleotides to the global ensemble bins
As stated above, the individual positions of the 12-mer MD trajectories do not have the same occupancy profile as the global ensemble. To describe the specific divergences from the global values, the ensemble occupancies at each of the 544 base positions in the 136 12-mers were computed. These occupancies were computed in reference to the same global ensemble bins as defined above (employing pooled data) but a 20%-occupancy of in each bin is no longer guaranteed (Figure SF1(b–d)).
Sequence to ensemble predictor: training and validation of DynaSeq
For the purpose of training and cross-validating DynaSeq, we used 65 ensemble features on the 544 positions, which form the desired output of a trained model. We described the sequence environment of each of the 544 base positions by the identity of the base at that location and its flanking bases, which formed the input for our training model. Each of the corresponding 65 values can be predicted by one support vector regression (SVR) model. Thus, we created 65 SVR models, each of which takes the sparse-encoded DNA sequence as the input and returns the ensemble occupancy for the central nucleotide position as the output. Once a trained model is ready, a strategy to convert ensemble into averaged structure and comparing predicted values of DNAshape and DynaSeq for an exhaustive list of 6-mers was developed. These steps are summarized below.
Sparse-encoding of DNA sequence
Machine-readable, unique representations of DNA sequences are sparse encoded, as in our previous works on nucleic acids and proteins24, 58, 59. In this work each base position (or its n th neighbor) is occupied by one of the four bases A, C, G or T. A four-dimensional vector- in which all but one dimension denoting the identity of the base are zero- represents these four possibilities. A DNA sequence segment is a systematic concatenation of these vectors encoding the occurrence of a given base at individual positions.
Training and cross-validation of DynaSeq
To ensure that the 544-training instances are not over-fitted, cross-validation was performed by separating trajectories from each of the 136 sequences in the MD data and training the data over 135 cases, and testing how well such models can make predictions for the left-out set of ensemble occupancies. All SVR models were implemented using e1071 package60 in the R programming environment, using RBF kernel and default cost and gamma values61. Finally a trained model of window size 5 can be thought of as a dictionary of 1024 5-mer sequences mapped to their corresponding 65-dimensional ensemble populations of 13 parameters. This dictionary of the current implementation of DynaSeq can be accessed from http://dynaseq.sciwhylab.org as stated in the abstract.
Computing average structure from predicted ensembles
DNAshape predicts 4 static values, whereas DynaSeq is trained to predict 65 values of the ensemble bin occupancies. To convert ensemble bin occupancies of a given base in a DNA sequence, we used a simple approach of computing the statistical average using the following formula.
where 〈Cij〉 is the predicted mean structure for the conformational parameter C at i th base-position in the sequence j and M k and C ijk are the mid-point values of the k th bin and their predicted occupancies respectively.
Comparing corresponding features in DNAshape and DynaSeq
To estimate how the predicted values from DNAshape compare with DynaSeq derived static values defined in this way, we created an exhaustive list of 6-mers (46 in number) and obtained predictions from both tools (see Results). Pearson’s coefficients of correlation between the two predicted values were used to assess the agreement between DNAshape and DynaSeq.
DynaSeq benchmarks on PDB structures and DREAM5 data on TF specificities
In contrast to DNAshape, DynaSeq predicts all conformational parameters sufficient to rebuild complete three-dimensional structure of DNA. We evaluated if the DynaSeq predicted structure of the ‘original’ or ‘native’ sequence from Protein Data Bank (PDB) is closer to its crystal structure, compared to the predictions from random sequences of the same length. Similarly, DynaSeq was evaluated if a model trained on DREAM5 training data could correctly recall TF-binding specificities in its test data. Detailed methods to perform both these step and corresponding additional results are provided in the Supplementary Material.
Evaluating predictability of TFBS from DynaSeq-derived features
Extracting genome-wide TFBS for 1312 TFs in ES cells from PIQ study
Genome-wide binding sites of 1312 TFs are available from a recent study establishing the directionality of binding in some TFs26. Binding site coordinate data was taken from the same study as available from related online resource located at (http://piq.csail.mit.edu/data/v1.3.calls/140906.mES.calls.tar.gz) (data was downloaded on October 1, 2014 and has been reorganized on the authors’ website since then). In the study authors eventually examined the binding sites of only 733 TFs after post processing to discard TFs with insignificant profile strength and merging sets of motifs with similar binding patterns. However, for the present study we have utilized the entire data set of 1312 TFs. Binding sites from both forward and reverse strands are selected from “calls” data and equally sized corresponding controls are sampled at low binding scores assigned by PIQ (0.25 or lower scores; with cutoffs adjusted if the number of reads at this cutoff was too small). Typically the number of binding sites and control in a TF ranges from around 100 to as many as tens of thousands. In the latter case, maximum number of binding sites considered was fixed at 2000, selected by random sampling.
Computing DynaSeq -predicted ensembles at each binding site and in the 200 upstream and downstream sequence positions
PIQ data consists of TFs with different motif sizes and there is no natural way to align all of them with respect to one another to develop a cumulative understanding of position dependent predictability of TFBS from DNA shape or dynamics. Nonetheless, motif start site provides a good reference point as regions following this are enriched in motif residues and away from it are depleted in it. Using motif start site as a reference point, we predicted 65-dimensional DynaSeq features at all DNA positions within 200 bases upstream and downstream from the start site. At any given sequence position, where we wish to determine the prediction performance, we utilized these predicted 65 DynaSeq features each for all the positions within a window. These features for a window are then concatenated to form the inputs of a new cross-validated prediction model employing elastic nets. Similar treatment was given to four-dimensional predictions from DNAshape i.e. prediction models for DNAshape-based features were also based on the predict shape features for all nucleotide positions within a window.
Evaluating DynaSeq performance on PIQ data
Using feature sets and DNA positions as described above, we created new cross-validated prediction models, whose inputs are shape or ensemble features of DNA sequence in a window and outputs are class labels indicating if the sequence is derived from a TFBS or a genomic control. For all such binding site prediction models, we used elastic net regularized logistic regression models, implemented in the R-package glmnet 62. Elastic nets provide robust models free from over-fitting with appropriate penalties for large number of features via its adjustable parameter alpha, which was selected to be 0.1 in all models being discussed here. In all cases a 10-fold cross-validation was used to estimate strictly independent performance of these models61. Elastic net implementation in glmnet produces multiple prediction models by adjusting a tunable parameter lambda. Out of all such models in each case, we have used the one with highest AUC for all comparisons (see Supplementary Methods SM2).
Training TFBS predictor with one parameter ensemble at a time
To assess the extent to which each of the 13 shape features studied in this work contribute to predictions, we repeated the PIQ TFBS prediction steps described above by creating multiple prediction models at each position of each TF. One model each was created for 5-dimensional ensemble of one conformational parameter at one time at each base position in the TFBS of each TF. Average AUC of all TFs for positions enriched in motif (motif start site and a fixed distance on 5′ sequence neighborhood) and remaining regions are considered. In addition, at each base position relative to motif start site, the name of the parameter whose ensemble gave the best prediction performance was retained and finally a frequency of occurrences of each of the 13 feature names corresponding to conformational parameters were compared.
References
Slattery, M. et al. Absence of a simple code: how transcription factors read the genome. Trends Biochem Sci 39, 381–399 (2014).
Zhou, T. et al. DNAshape: a method for the high-throughput prediction of DNA structural features on a genomic scale. Nucleic Acids Res 41, W56–62, doi:10.1093/nar/gkt437 (2013).
Lazarovici, A. et al. Probing DNA shape and methylation state on a genomic scale with DNase I. Proc Natl Acad Sci USA 110, 6376–6381, doi:10.1073/pnas.1216822110 (2013).
Rohs, R. et al. Origins of specificity in protein-DNA recognition. Annu Rev Biochem 79, 233–269, doi:10.1146/annurev-biochem-060408-091030 (2010).
Gershenzon, N. I., Stormo, G. D. & Ioshikhes, I. P. Computational technique for improvement of the position-weight matrices for the DNA/protein binding sites. Nucleic Acids Res 33, 2290–2301, doi:10.1093/nar/gki519 (2005).
Tan, K., McCue, L. A. & Stormo, G. D. Making connections between novel transcription factors and their DNA motifs. Genome Res 15, 312–320, doi:10.1101/gr.3069205 (2005).
Benos, P. V., Lapedes, A. S. & Stormo, G. D. Is there a code for protein-DNA recognition? Probab(ilistical)ly …. BioEssays 24, 466–475 (2002).
Stormo, G. D. DNA binding sites: representation and discovery. Bioinformatics 16, 16–23 (2000).
Chen, Q., Hertz, G. & Stormo, G. D. MATRIX SEARCH 1.0: a computer program that scans DNA sequences for transcriptional elements using a database of weight matrices. Computer Applications in the Biosciences: CABIOS 11, 563–566 (1995).
Barozzi, I. et al. Coregulation of Transcription Factor Binding and Nucleosome Occupancy through DNA Features of Mammalian Enhancers. Mol Cell 54, 844–857, doi:10.1016/j.molcel.2014.04.006 (2014).
Yang, L. et al. TFBSshape: a motif database for DNA shape features of transcription factor binding sites. Nucleic Acids Res 42, D148–155, doi:10.1093/nar/gkt1087 (2014).
Dror, I., Zhou, T., Mandel-Gutfreund, Y. & Rohs, R. Covariation between homeodomain transcription factors and the shape of their DNA binding sites. Nucleic Acids Res 42, 430–441, doi:10.1093/nar/gkt862 (2014).
Rohs, R. et al. The role of DNA shape in protein-DNA recognition. Nature 461, 1248–1253, doi:10.1038/nature08473 (2009).
Weirauch, M. T. et al. Evaluation of methods for modeling transcription factor sequence specificity. Nat Biotechnol 31, 126–134, doi:10.1038/nbt.2486 (2013).
Wingender, E. The TRANSFAC project as an example of framework technology that supports the analysis of genomic regulation. Brief Bioinform 9, 326–332, doi:10.1093/bib/bbn016 (2008).
Hume, M. A., Barrera, L. A., Gisselbrecht, S. S. & Bulyk, M. L. UniPROBE, update 2015: new tools and content for the online database of protein-binding microarray data on protein-DNA interactions. Nucleic Acids Res 43, D117–122, doi:10.1093/nar/gku1045 (2015).
Arauzo-Bravo, M. J. & Sarai, A. Indirect readout in drug-DNA recognition: role of sequence-dependent DNA conformation. Nucleic Acids Res 36, 376–386, doi:10.1093/nar/gkm892 (2008).
Fujii, S., Kono, H., Takenaka, S., Go, N. & Sarai, A. Sequence-dependent DNA deformability studied using molecular dynamics simulations. Nucleic Acids Res 35, 6063–6074, doi:10.1093/nar/gkm627 (2007).
Ahmad, S., Kono, H., Araúzo-Bravo, M. J. & Sarai, A. ReadOut: structure-based calculation of direct and indirect readout energies and specificities for protein–DNA recognition. Nucleic Acids Res 34, W124–W127 (2006).
Araúzo-Bravo, M. J., Fujii, S., Kono, H., Ahmad, S. & Sarai, A. Sequence-dependent conformational energy of DNA derived from molecular dynamics simulations: toward understanding the indirect readout mechanism in protein-DNA recognition. Journal of the American Chemical Society 127, 16074–16089 (2005).
Kono, H. & Sarai, A. Structure-based prediction of DNA target sites by regulatory proteins. Proteins 35, 114–131 (1999).
Selvaraj, S., Kono, H. & Sarai, A. Specificity of Protein-DNA Recognition Revealed by Structure-based Potentials: Symmetric/Asymmetric and Cognate/Non-cognate Binding. J Mol Biol 322, 907–915 (2002).
Gromiha, M. M., Siebers, J. G., Selvaraj, S., Kono, H. & Sarai, A. Intermolecular and intramolecular readout mechanisms in protein–DNA recognition. J Mol Biol 337, 285–294 (2004).
Ahmad, S. Sequence-dependence and prediction of nucleotide solvent accessibility in double stranded DNA. Gene 428, 25–30 (2009).
Lu, X. J. & Olson, W. K. 3DNA: a versatile, integrated software system for the analysis, rebuilding and visualization of three-dimensional nucleic-acid structures. Nature protocols 3, 1213–1227, doi:10.1038/nprot.2008.104 (2008).
Sherwood, R. I. et al. Discovery of directional and nondirectional pioneer transcription factors by modeling DNase profile magnitude and shape. Nat Biotechnol 32, 171–178, doi:10.1038/nbt.2798 nbt.2798 [pii] (2014).
Limin Angela Liu, P. B. Atomistic modeling of protein–DNA interaction specificity: progress and applications. Current Opinion in Structural Biology 22, 397–405 (2012).
Stolovitzky, G., Monroe, D. G. & Califano, A. Dialogue on Reverse-Engineering Assessment and Methods. Annals of the New York Academy of Sciences 1115, 1–22, doi:10.1196/annals.1407.021 (2007).
Ma, W., Yang, L., Rohs, R. & Noble, W. S. DNA sequence + shape kernel enables alignment-free modeling of transcription factor binding. Bioaxive, https://doi.org/10.1101/089441 (2016).
El Hassan, M. A. & Calladine, C. R. Propeller-Twisting of Base-pairs and the Conformational Mobility of Dinucleotide Steps in DNA. Journal of Molecular Biology 259(1), 95–103 (1996).
Krueger, A., Protozanova, E. & Frank-Kamenetskii, M. D. Sequence-Dependent Basepair Opening in DNA Double Helix. Biophysical Journal 90(9), 3091–3099 doi:10.1529/biophysj.105.078774 (2006).
Akan, P. & Deloukas, P. DNA sequence and structural properties as predictors of human and mouse promoters. Gene 410(1), 165–176 doi:10.1016/j.gene.2007.12.011 (2008).
Lipovich, L. et al. Developmental changes in the transcriptome of human cerebral cortex tissue: long noncoding RNA transcripts. Cerebral cortex 24, 1451–1459, doi:10.1093/cercor/bhs414 (2014).
Timsit, Y. DNA-directed base pair opening. Molecules 17, 11947–11964, doi:10.3390/molecules171011947 (2012).
Dans, P. D., Walther, J., Gomez, H. & Modesto, O. Multiscale simulation of DNA. Current Opinion in Structural Biology 37, 29–45 (2016).
Dans, P. D. et al. How accurate are accurate force-fields for B-DNA? Nucleic Acids Res, doi: 10.1093/nar/gkw1355 (2017).
Hospital, A. et al. BIGNASim: a NoSQL database structure and analysis portal for nucleic acids simulation data. Nucleic Acids Res 44, D272–278, doi:10.1093/nar/gkv1301 (2016).
Dans, P. D. et al. Unraveling the sequence-dependent polymorphic behavior of d(CpG) steps in B-DNA. Nucleic Acids Res. doi:10.1093/nar/gku809 (2014).
Dans, P. D., Perez, A., Faustino, I., Lavery, R. & Orozco, M. Exploring polymorphisms in B-DNA helical conformations. Nucleic Acids Res 40, 10668–10678, doi:10.1093/nar/gks884 (2012).
Dror, I., Golan, T., Levy, C., Rohs, R. & Mandel-Gutfreund, Y. A widespread role of the motif environment in transcription factor binding across diverse protein families. Genome Research 25, 1268–1280 (2015).
Jolma, A. et al. DNA-binding specificities of human transcription factors. Cell. 2013 Jan 17;152(1–2):327-39. Cell 152, 327–329 (2013).
Hutchins, A. P. et al. Distinct transcriptional regulatory modules underlie STAT3’s cell type-independent and cell type-specific functions. Nucleic Acids Res 41, 2155–2170, doi:10.1093/nar/gks1300gks1300 [pii] (2013).
Fogg, J. et al. Bullied no more: when and how DNA shoves proteins around. Q Rev Biophys 45, 257–299, doi:10.1017/S0033583512000054 (2012).
Pan, Y., Tsai, C. J., Ma, B. & Nussinov, R. How do transcription factors select specific binding sites in the genome? Nature Structural & Molecular Biology 16, 1118–1120 (2009).
Pan, Y., Tsai, C. J., Ma, B. & Nussinov, R. Mechanisms of transcription factor selectivity. Trends in genetics: TIG 26, 75–83, doi:10.1016/j.tig.2009.12.003 (2010).
Ma, B., Tsai, C. J., Pan, Y. & Nussinov, R. Why does binding of proteins to DNA or proteins to proteins not necessarily spell function? ACS chemical biology 5, 265–272, doi:10.1021/cb900293a (2010).
Pan, Y. & Nussinov, R. Cooperativity dominates the genomic organization of p53-response elements: a mechanistic view. PLoS Comput Biol 5, e1000448, doi:10.1371/journal.pcbi.1000448 (2009).
Chen, I. Allostery through DNA. Nat Struct Mol Biol 20, 410, doi:10.1038/nsmb0413-410 (2013).
Kim, S. et al. Probing allostery through DNA. Science 339, 816–819, doi:10.1126/science.1229223 (2013).
Chaires, J. B. Allostery: DNA does it, too. ACS chemical biology 3, 207–209, doi:10.1021/cb800070s (2008).
Pan, Y. & Nussinov, R. Lysine120 interactions with p53 response elements can allosterically direct p53 organization. PLoS Comput Biol 6, doi: 10.1371/journal.pcbi.1000878 (2010).
Travers, A. & Muskhelishvili, G. A common topology for bacterial and eukaryotic transcription initiation? EMBO reports 8, 147–151 (2007).
Krueger, A. & Protozanova, E. & Frank-Kamenetskii. Sequence-dependent base pair opening in DNA double helix. Biophysical Jounal 90, 3091–3099 (2006).
Arauzo-Bravo, M. J., Fujii, S., Kono, H., Ahmad, S. & Sarai, A. Sequence-dependent conformational energy of DNA derived from molecular dynamics simulations: toward understanding the indirect readout mechanism in protein-DNA recognition. J Am Chem Soc 127, 16074–16089, doi:10.1021/ja053241l (2005).
Beveridge, D. L., Cheatham, T. E. 3rd & Mezei, M. The ABCs of molecular dynamics simulations on B-DNA, circa 2012. Journal of biosciences 37, 379–397 (2012).
Perez, A. et al. Refinement of the AMBER force field for nucleic acids: improving the description of α/γ conformers. Biophysical Journal 92, 3817–3829 (2007).
Ivan Ivani et al. Parmbsc1: a refined force field for DNA simulations. Nature methods 13, 55–58, doi:10.1038/nmeth.3658 (2016).
Ahmad, S., Gromiha, M. M. & Sarai, A. Analysis and prediction of DNA-binding proteins and their binding residues based on composition, sequence and structural information. Bioinformatics 20, 477–486 (2004).
Andrabi, M., Mizuguchi, K., Sarai, A. & Ahmad, S. Prediction of mono- and di-nucleotide-specific DNA-binding sites in proteins using neural networks. BMC Structural Biology 9, 30 (2009).
e1071: Misc Functions of the Department of Statistics (e1071), TU Wien (2010).
R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, Austria, 2014).
Friedman, J., Hastie, T. & Tibshirani, R. glmnet: Lasso and elastic-net regularized generalized linear models. R package version 1 (2009).
Acknowledgements
This work has been supported by a grant by University for Potential of Excellence (UPoE-II) scheme of the University Grants Commission, India to S.A. This work has also been supported by a grants-in-aid (kaken-hi #15K00419) program of Japanese Society for Promotion of Science to S.A. This work has also been supported by Grants-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan [JP25116003 and JP26330339 to H.K.] and Platform for Drug Discovery, Informatics, and Structural Life Science from Japan Agency for Medical Research and Development (AMED) to H.K. This study was in part supported by Grants-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science, and Technology (Grant Numbers 25430186 and 25293079) and from the Ministry of Health, Labor, and Welfare to K.M. This project has been funded in whole or in part with Federal funds from the National Cancer Institute, National Institutes of Health, under contract number HHSN261200800001E. The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services, nor does mention of trade names, commercial products, or organizations imply endorsement by the U.S. Government. This research was supported (in part) by the Intramural Research Program of the NIH, National Cancer Institute, Center for Cancer Research.
Author information
Authors and Affiliations
Contributions
S.A. conceived and designed the main components of this study and implemented it together with M.A. H.K. provided MD. data and helped in analyzing other results. S.A., M.A. and A.P.H. prepared the manuscript with discussions and critical comments from R.N., D.M.S., H.K. and K.M. All authors participated in discussions on all aspects of the manuscript and read, improved and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Andrabi, M., Hutchins, A.P., Miranda-Saavedra, D. et al. Predicting conformational ensembles and genome-wide transcription factor binding sites from DNA sequences. Sci Rep 7, 4071 (2017). https://doi.org/10.1038/s41598-017-03199-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-03199-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.