Background & Summary

As our global system transitions to renewable energy, the demand for efficient and affordable energy storage will continue to grow. Currently, lithium-ion batteries (LIBs) bear the major load of electrochemical energy storage requirements due to their high energy density and cyclability1. However, it remains unclear whether the production of lithium-ion batteries can scale at a rate and cost that will meet future needs2,3. In the search for alternatives to lithium, fluoride-ion batteries (FIBs) are promising based on several factors. First, they offer higher theoretical energy densities than current LIBs (~1,000–2,200 Wh/kg vs 220–650 Wh/kg)2,4. Second, since fluorine is the most electronegative element, fluoride has high redox stability, which enables battery operation within a large electrochemical window. Third, fluoride and many of its prospective electrode materials are more abundant and less expensive than those for lithium4.

Significant work has been accomplished in discovering liquid electrolytes5,6,7,8 and high-performance anodes9,10 for FIBs. Although additional investigation in these components is still critical, there is an especially strong need to identify promising cathode materials. To guide previous cathode discovery, the primary heuristic that has been used is fluoride affinity. During the FIB discharge process, fluoride ions (F−) spontaneously leave the cathode and migrate through the electrolyte to the anode. For this to be spontaneous, the anode must have higher affinity for fluoride than the cathode. Thus, a general design rule for fluoride electrodes is that more electronegative elements such as Cu or Bi are promising for cathodes, and more electropositive elements such as Mg or Y are promising for anodes11,12,13,14,15. These simple guidelines have inspired considerable cathode work using the binary metal fluorides like Cu/CuF2, Fe/FeF3, Sn/SnF2 and particularly Bi/BiF312,16,17,18,19,20. However, the realization of more complex compositions creates an opportunity to alter a material’s physical and electronic properties for cathode use beyond the limited scope of binary compositions. Recent studies have employed three and four elements-containing oxide cathode materials (La2NiO4, LaSrMnO4, La2CoO4, BaFeO2.5)14,21,22,23 to begin expanding this design space. Despite these advances, only a small number of more complex compositions have been investigated. In this work, we describe the first systematic exploration of compounds that assesses the cathodic capability of all known ternary fluoride materials.

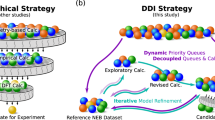
With thousands of possible ternary metal fluorides, a method for selecting candidates for experimental discovery becomes paramount. The recent development of large crystal structure databases like Materials Project24 makes computational screening an attractive first step for this purpose. Here, we utilize computational filtering techniques to search for existing ternary metal fluorides in the Materials Project database that may function as cathodes for FIBs. Our search aims to identify fluorinated and defluorinated structure pairs. Identification of fluorinated/defluorinated pairs yields a dataset of possible charged and discharged states for a cathode material. This broader filtering is broken down into two smaller searches: fully defluorinated candidates and partially defluorinated candidates. These are further narrowed down by considering calculated stability and presence of disproportionation reactions along the defluorination pathway. In Fig. 1, we present a simplified diagram for this filtering algorithm.

Fig. 1
figure 1

The filtering steps used to obtain the final dataset. Several quaternary materials were also identified as promising cathodes and included in this dataset.

Full size image

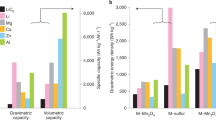
A collection of properties was also calculated for each structure pair including redox potentials vs. Li/LiF and vs. F2, specific capacity, percent expansion between defluorinated and fluorinated forms, energy densities, and cost approximations. Redox potentials vs. Li/LiF for direct reaction pairs ranged from −0.92 V (Ca5(PO4)3F/Ca5(PO4)3) to 5.77 V (LiAgF6/ LiAgF4) with an average of 2.9 V. Specific capacity ranged from 6.4 mAh/g (RbSnF3/RbSn2.94) to 758 mAh/g (NClOF4/NClO) with an average of 150 mAh/g. Figure 2a,b illustrate the relationship between energy density (Wh/kg) and log10($/mol of mobile F) with a colorimetric scale based on percent expansion for each pair. Log10($/mol of mobile F) is used rather than $/mol to visually counteract the Pareto-like distribution of low-cost materials and account for charge transfer capacity. Structures are distributed along the cost axis with a range that spans five orders of magnitude. Most structures have energy densities between 0–900 Wh/kg with moderate expansion between 7–40%. Figure 2b is a zoomed in view of 2a at the desired property overlap of high energy density and low price with points identified by the fluorinated structure and fluoride content of the defluorinated structure.

Fig. 2
figure 2

Cathodes demonstrating a direct reaction between fluorinated/defluorinated pairs. All 168 pairs are shown in (a). In (b) the graph is zoomed in to highlight the high energy density and low-cost materials. Each pair is identified by the fluorinated structure and “Fx” which indicates the fluoride content of the defluorinated structure. The volumetric expansion of each pair is indicated by the color scale. Values of LiCoO2 (LIB cathode) are also included for comparison.

Full size image

Some fluorinated structures appear more than once with different defluorinated structures, such as CaNiF6/CaNiF5 and CaNiF6/CaNiF4. The presence of these multi-redox capable fluorinated structures highlights differences in chemical potential along a given defluorination pathway. When these materials are present, they are likely to also exhibit a multistep voltage profile. This is observed in the Ca-Ni-F system, where CaNiF6/CaNiF5 is 5.50 V vs. Li/LiF, CaNiF5/CaNiF4 is 4.78 V, and CaNiF6/CaNiF4 is 5.14 V. Although the two-electron transfer of CaNiF6/CaNiF4 pair is likely kinetically complicated compared to the single-electron transfer of the two former pairs, the variations in calculated potentials appear systematic. This type of consideration is expected to play an important role in cathode performance. Our dataset allows for straightforward identification of these and other types of interesting trends.

Structural factors must also be considered in assessing the viability of candidates. Although the NClOF4/NClO, S(OF)2/SO2, and As(BrF2)3/AsBr3 pairs shown in 2b may seem promising, these materials are molecular crystals. These crystals likely lack the conductivity and mechanical stability needed to function as an electrode. Thus, these graphs provide only a snapshot of some properties and should not be taken as the only important criteria. Metrics for the common LIB cathode LiCoO2 are also displayed on the graph to orient the reader. The theoretical energy density for LiCoO2 is calculated in the same manner as the energy densities for the fluorination pairs, while the experimental energy density for LiCoO2 references current literature values3. The discrepancy in energy density between the theoretical and experimental values of LiCoO2 has been attributed to the incomplete deintercalation of Li from LiCoO2, which is also accounted for in the cost calculation25.

Although our dataset may encourage researchers to focus on materials with energy densities above those of current LIB technology, we also note that other characteristics can be important. These include ionic and electrical conductivity, chemical compatibility with an electrolyte, electrochemical stability, and material recyclability. Some of these additional criteria are also included in our dataset and we encourage researchers to evaluate the dataset holistically. On a broader scale, we hope that this dataset can be used to guide experimental selection of promising new FIB cathodes.

Methods

The dataset was produced using the Simulated Materials Ecosystem (Simmate)26 and Materials Project API24. Simmate combines many crystal structure databases in one software package, including Materials Project, the Crystallography Open Database (COD)27, the Joint Automated Repository for Various Integrated Simulations (JARVIS)28, and the Open Quantum Materials Database (OQMD)29. At the time of writing, the Materials Project database contains over 145,000 crystal structures. The Materials Project database (via Simmate) was initially filtered to include all fluoride-containing structures with more than two elements and a hull energy less than or equal to 75 meV (6,525 structures). This cut-off was chosen based on known errors in DFT formation enthalpies and is discussed further in Technical Validation. To ensure that each composition was represented solely by the most stable phase, these structures were sorted by ascending hull energy and entries after the first occurrence of a given reduced formula were excluded. This list comprised the fluorinated half of all possible fluorinated/defluorinated pairs (4,389 structures).

Complete defluorination

A copy of each fluorinated entry was made, and all fluorine atoms were removed from the copied structure. This represented the other half of a possible fluorinated/defluorinated pair. The reduced formula of the defluorinated copy was then compared to the full Materials Project database. If an entry on Materials Project had the same reduced formula and was within 75 meV of hull, the entry was identified as a possible match. Multiple phases of the same composition also appeared during this step and were addressed in a similar manner as above to identify the most stable phase. There were 425 fluorinated/fully defluorinated pairs identified after this step.

Partial defluorination

Identification of partially defluorinated structure pairs was more involved than complete defluorination, as structural compositions along the full defluorination pathway had to be considered. The Materials Project database was searched for each entry in the initial fluorinated list, where structures with the same elements as the fluorinated entry, with the same ratios of non-fluoride elements, and within 75 meV of hull, were identified as possible defluorinated pairs. For structures with identical compositions, we filtered the dataset to select the lowest energy phase. This resulted in 382 fluorinated/partially defluorinated pairs. Thus, a total of 807 fluorinated/defluorinated pairs were taken forward through the remaining analyses.

Disproportionation reactions

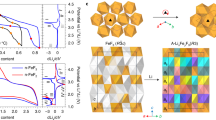
The ternary phase diagram of a three-element system is characterized by nodes and tie-lines. Nodes are specific stable (or metastable) structures and tie-lines represent two-phase equilibria between these structures30. When a fluorinated/defluorinated pair is identified, it becomes imperative to check the associated phase diagram for a tie-line connecting the two, which shows that there is a direct reaction between the two phases. In the absence of a direct reaction, the fluorinated/defluorinated pair will disproportionate into two or more additional phases at global compositions that are intermediate between the two pairs. To illustrate these direct and indirect reactions, in Fig. 3 we show the phase diagrams and reaction coordinates for two possible fluorinated/defluorinated systems. It is useful to interpret the tie-line (3a) and dotted-line (3b) connecting the two fluorinated/defluorinated structures on the phase diagram as top-down views of reaction coordinates. Each diagram and reaction coordinate shows an example of a direct (3a,c, KBrF4/KBr) and indirect (3b,d, NaBiF6/NaBi) reaction. In 3a the KBrF4/KBr pair has a tie-line between the two target structures (circled in green), indicating that the structures convert from one to the other as fluorine content changes via a direct reaction. This is reflected in the interface reaction coordinate (3c) with a straight, horizontal line indicating that the pair does not decompose into other phases. However, there is no tie-line connecting the NaBiF6/NaBi pair (3b, dotted line drawn in to highlight where a tie-line would exist). In fact, there are two other tie-lines that lie between the pair. This means that at global compositions between NaBiF6 and NaBi, the system will at least partially disproportionate into NaF, BiF3, and Bi. The interface reaction coordinate (3d) confirms that these disproportionation reactions are thermodynamically favourable, indicated by the decrease in reaction energy per atom. Once disproportionation occurs, the presence of multiple heterogeneous phases makes it less likely to form the desired product (eg NaBi), even if the global composition exactly matches NaBi. In this event, the amount of active material and the cathode’s cyclability will decrease.

Fig. 3
figure 3

Examples of (a,c) direct and (b,d) indirect interface reactions for fluorinated/defluorinated structure pairs. In (a) there is a single tie-line connecting the fluorinated (KBrF4) and defluorinated (KBr) structures. In (b) the drawn-in dotted-line between NaBiF6 and NaBi crosses over the tie-lines connecting NaF/BiF3 and NaF/Bi, leading to disproportionation to the phases on either end of the crossed tie-lines as F is removed. The interface reaction coordinates (c/d) reflect these predictions.

Full size image

To assess each fluorinated/defluorinated pair for the presence of direct or indirect reactions, we used pymatgen’s interface reaction function31. This function used the fluorinated and defluorinated structure pair as the two reactants. If there was no thermodynamically favorable reaction between the pair, the function gave the two original structures as “products” of the reaction. This indicated a direct reaction. If an indirect (disproportionation) reaction occurred, the function returned a list of disproportionation products. Of the 807 pairs, 168 had direct reactions. The first 58 of these were complete defluorination pairs, which was 14% of the original 425 complete defluorination pairs. The remaining 110 direct reactions were partial defluorination pairs, or 29% of the original 382 partial defluorination pairs.

Relevant properties were calculated for the 168 direct reaction structure pairs:

Potentials

It is known that open circuit voltages can be predicted for lithium-ion battery materials using energies calculated from DFT + U methods32. It is common to refer to voltages against metallic lithium in these systems, which can be considered the natural limit for the usability of a component in a lithium-ion battery. In fluoride-ion batteries, F2 can be used analogously to calculate open circuit voltages for materials in these systems23. These potentials can be calculated for materials by using a hypothetical F2 electrode according to the following reaction:

$${\rm{AB}}+\frac{x}{2}{{\rm{F}}}_{2}\to {{\rm{ABF}}}_{{\rm{x}}}$$
(1)

While this reaction is useful theoretically, the realization of a gaseous F2 electrode is unlikely. Moreover, as written, the potentials obtained are oxidation potentials rather than reduction potentials. To provide a more conventional perspective, we also calculate potentials using the Li/LiF pair as an anode according to:

$${{\rm{ABF}}}_{{\rm{x}}}+{\rm{x}}\,{\rm{Li}}\to {\rm{AB}}+{\rm{x}}\,{\rm{LiF}}$$
(2)

For this reaction, a good cathode material corresponds to a high voltage. The voltages for these two reactions can be calculated starting from the Nernst equation:

$$Potential=-\frac{\Delta {G}_{{\rm{rxn}}}}{xF}$$
(3)

Where ΔGrxn is the change in Gibbs free energy of the reaction (J/mol), x is the number of fluoride ions transferred, and F is Faraday’s constant. Volume (PΔVrxn) and entropic (TΔSrxn) effects can be neglected for the calculation of ΔGrxn (=ΔUrxn + PΔVrxn – TΔSrxn) because PΔVrxn is on the order of 10−5 eV and TΔSrxn is on the scale of thermal energy, which are both much smaller than ΔUrxn (~101 eV). Thus, ΔGrxn can be reasonably obtained from the change in internal energy (ΔUrxn)33,34,35. The Materials Project calculates internal energy for every entry in its database using DFT + U, so ΔGrxn can be calculated from these values for (1) and (2) respectively according to:

$$\Delta {{\rm{G}}}_{{\rm{rxn}}}\approx \Delta {{\rm{U}}}_{{\rm{rxn}}}=({{\rm{U}}}_{{\rm{ABFx}}})-\left({{\rm{U}}}_{{\rm{AB}}}+\frac{x}{2}{{\rm{U}}}_{{\rm{F}}2}\right)$$
(4)

and

$$\Delta {{\rm{G}}}_{{\rm{rxn}}}\approx \Delta {{\rm{U}}}_{{\rm{rxn}}}=\left({{\rm{U}}}_{{\rm{AB}}}+{{\rm{xU}}}_{{\rm{LiF}}}\right)-\left({{\rm{U}}}_{{\rm{ABFx}}}+{\rm{x}}\,{{\rm{U}}}_{{\rm{Li}}}\right)$$
(5)

where Uy is the internal energy of each compound. Because Materials Project provides internal energy values in eV rather than J, Faraday’s constant can be dropped from (3). Thus, potentials vs. F2 and vs. Li/LiF were calculated from -ΔGrxn/x. These oxidation potentials range from −0.35 to 7.07 V vs. F2 and the reduction potential range from −0.92 to 6.50 V vs. Li/LiF. We use the potentials vs. Li/LiF for energy density calculations. Graphite and LiC6 were used instead of Li and LiF to calculate the potential for LiCoO2/CoO2 (LIB cathode).

Volume per fluorine (Å3)

Volume per fluoride was calculated using the volume per formula unit of the fluorinated structure divided by the difference in fluorine atoms between the fluorinated and defluorinated structures.

Percent expansion

The expansion from the defluorinated to fluorinated structure was calculated by dividing the fluorinated volume per formula unit by the defluorinated volume per formula unit, subtracting 1, and then multiplying by 100%.

Gravimetric capacity (mAh/g)

The gravimetric capacity for each fluorinated structure was calculated according to Faraday’s Law:

$$Capacity=\frac{n\ast F}{C\ast MW}$$

Where n is the number of charge carriers (fluoride ions), F is Faraday’s constant (96,485.3 C/mol), C is a conversion factor (3.6 C/mAh), and MW is the molecular weight of the fluorinated structure in g/mol.

Gravimetric energy density (Wh/kg)

The gravimetric energy density was obtained by multiplying the gravimetric capacity by voltage.

Volumetric energy density (Wh/L)

The volumetric energy density was calculated by multiplying the gravimetric energy density by the density of the fluorinated material.

Cost analysis

A cost analysis was done for each material using pymatgen’s cost module. Costs were not calculated for Rb2UF7 due to issues with the module in calculating a phase diagram containing U. For readers interested in replicating these results, column headers must be deleted from the ‘costdb_elements_new.csv’ file before using for the analysis to work properly.

Transport barrier (eV)

When data was available, the activation energy for fluoride transport is presented36.

The difference in atoms per formula unit between each structure pair, which is used to calculate the number of fluorides transferred and other properties, assumes that each reduced formula has the same number of each type of non-F atoms. This is not true for all structures, however. Therefore, we counted the number of non-fluoride atoms in each pair and rescaled the reduced formulas so that the number of non-fluoride atoms remained unchanged.

Several 4- and 5-element containing pairs were also identified including Ca5(PO4)3F, Ca5(VO4)3F, Pb5(PO4)3F, Pb5(VO4)3F, LiVPO4F, LiMnPO4F, LiFePO4F, CeAsO4F, BaAlGeF, TmSeO3F, LuSeO3F, LiCrPO4F, Sr2FeO3F, Ca6Al3(AlO4)4F, Na3MoO4F, YSeO3F, Li2CoO2F, TiH8(NF3)2, ReSbOF10, MgAs2(XeF9)2. The filtering criteria worked correctly for these structures and were left in as additional datapoints.

Data Records

The produced datasets are available in Figshare37 and at the ternary_f_cathodes page on Github. The datasets are provided as two CSV files, one containing all 807 pairs and one containing the 168 direct reaction pairs. The modified cost spreadsheet is also provided. The python script file used to create the dataset is available on the Github page. Table 1 provides the list of column titles in the files and a description of each.

Table 1 List of column titles in cathode datasets with descriptions.
Full size table

Technical Validation

The data presented is taken from Simmate and Materials Project databases or calculated directly according to the methods described above. Many of the reported properties rely on DFT internal energy calculations, which are known to incorporate systematic and random error. Particularly, the approximate DFT functionals result in errors due to changes of electron self-interaction in localized transition metal states. This originates from changes in oxidation state upon product formation from discrete reactants. Known binding errors of diatomic molecules (F2, O2, N2, Cl2, H2) using LDA and GGA functionals further complicate the calculation of accurate internal energies. This is mitigated in transition metal cations by applying a Hubbard U value to d or f orbitals and constant energy corrections based on experimental comparison for anionic species (F−, O2−, S2−…). Materials Project employs corrections for both errors with a mix of GGA and GGA + U functionals as well as anion-specific corrections38,39,40,41,42. Our calculations used these corrections, which reduces the error in GGA or GGA + U formation enthalpies from ≈ 175–450 meV/atom (uncorrected) to ≈ 45–55 meV/atom (corrected). The magnitude of these energies supported the chosen filtering value of 75 meV above hull, slightly above the noted correction error. The calculation of cathode potential relies on internal energies of multiple structures, which somewhat increases the total error. These errors are small compared to the potentials that are spanned across all cathodes, thereby supporting our ability to sort and rank cathode according to the predicted potential. The uncertainties of activation energies for F-ion conduction were described previously36.

Adaptations were made to pymatgen’s cost module for more accurate price approximations. Original module reference prices are based on pure elemental forms, which misrepresent the predicted costs because many elements can be obtained as salts for a much lower cost. Therefore, all elemental costs are obtained from the Wikipedia “Prices of chemical elements” page, which more accurately takes this into account. The prices listed on Wikipedia are primarily average market prices for bulk trade, but when this data is not available the price of a compound is used, per mass of the given element.