Abstract
In the application of deep learning on optical coherence tomography (OCT) data, it is common to train classification networks using 2D images originating from volumetric data. Given the micrometer resolution of OCT systems, consecutive images are often very similar in both visible structures and noise. Thus, an inappropriate data split can result in overlap between the training and testing sets, with a large portion of the literature overlooking this aspect. In this study, the effect of improper dataset splitting on model evaluation is demonstrated for three classification tasks using three OCT open-access datasets extensively used, Kermany’s and Srinivasan’s ophthalmology datasets, and AIIMS breast tissue dataset. Results show that the classification performance is inflated by 0.07 up to 0.43 in terms of Matthews Correlation Coefficient (accuracy: 5% to 30%) for models tested on datasets with improper splitting, highlighting the considerable effect of dataset handling on model evaluation. This study intends to raise awareness on the importance of dataset splitting given the increased research interest in implementing deep learning on OCT data.
Similar content being viewed by others
Introduction
The evaluation of deep learning models, and machine learning methods in general, aims at providing an unbiased description of model performance. Given a pool of data suitable for studying a hypothesis (e.g., classification, regression or segmentation), different splits of the data are commonly created for model training, model hyper-parameter tuning (validation set) and model assessment (testing set). This translates to having a part of the data used to fit model parameters and tune model hyperparameters, and another set to assess model generalization on unseen data1. Disregarding the choice of having separate validation and testing splits2, the strategy used to generate the testing set from the original pool of data can have a large impact on the assessment of the model’s final performance. Several studies have investigated the effect of the relative size between training, validation and/or testing sets1,3 on model performance, as well as how training and validation sets can be used via resampling techniques, such as cross-validation, during model training1,4. More importantly, it is widely accepted that no overlap should exist between the samples used for model fitting and hyperparameter tuning, and those belonging to the testing set. If overlap is present, the model performance will be biased and uninformative with respect to the generalization capabilities of the model to new samples. However, although trivial, when implementing data splitting strategies, the overlap between training and testing sets can be easily overlooked. This is specifically more common in those applications where, due to hardware limitations or model design choices, the data from one subject (or acquisition) is used to obtain multiple dimensionally smaller samples used for model training and testing. An example of such a scenario is the slicing of a 3D volume into 2D images. In these cases, the overlap between training and testing sets results from having 2D images from the same subject (or acquisition) belonging to both sets. A proper splitting must therefore be performed on the volume or subject level and not on the slice level.
Nowadays, machine learning methods, especially convolutional neural networks (CNNs) and deep learning algorithms, are widely used in research to analyze medical image data. A plethora of publications describe CNN implementations on a variety of both 2D and 3D medical data5,6,7. Reliable evaluation of such methods is paramount since this informs the research community on the models’ performance, allows meaningful comparison between methods, and to a greater extent indicates which research questions might be worth further investigation. In this regard, many medical image analysis challenges were established that aim at providing an unbiased platform for the evaluation and ranking of different methods on a common and standard testing dataset. Despite the many limitations of the medical image analysis challenges, including missing information regarding how the ground truth was obtained, their contribution towards a more transparent and reliable evaluation of deep learning methods for medical image applications is valuable8.
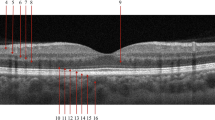
However, not all implementations can be evaluated through dedicated challenges and unbiased datasets. Thus, when such third-party evaluation platforms are not available, it is the responsibility of the researchers performing the investigation to evaluate their methods thoroughly. As for the case of many of the reviewed medical image analysis challenges8, one aspect that is sometimes missing or not well described is how the testing dataset is generated from the original pool of data. Moreover, there are examples where the preparation of the testing dataset was described, but its overlap with the training set was not considered9,10,11,12,13, undermining the reliability of the reported results. Focusing on deep-learning applications for OCT, depending on the acquisition set-up, volumes are usually acquired with micrometer resolution in the x, y and z directions in a restricted field of view, with tissue structures that are alike and affected by similar noise. This results in consecutive slices having a high similarity, in both structure and noise. Figure 1 shows a schematic of an OCT volume along with examples of two consecutive slices from OCT volumes from three open-access datasets14,15,16.
Schematic of an OCT volume with examples of consecutive slices (b-scans) from the three open-access OCT datasets used in this study. In (a) consecutive 2D b-scans rendering a 3D OCT volume are pictured. Here an example from the AIIMS dataset14 is used for illustrative purposes. In (b) the consecutive b-scans separated by ~18 micrometers are examples of healthy breast tissue (Patient 15, volume 0046, slices 0075 and 0076) from the AIIMS dataset14. In (c) images of healthy retina from Srinivasan’s dataset16 (folder NORMAL5 slices 032 and 033) can be seen. In (d) consecutive images of retina affected by choroidal neovascularization (CNV 81630-33 and 81630-34) from the Kermany’s OCT2017 version 2 dataset15 are shown. Note that the b-scans from both Kermany’s and Srinivasan’s datasets are given with data augmentation originally applied.
Most of the reviewed literature implementing deep learning on OCT data used 2D images from scanned volumes, where two methods were commonly used to split the pool of image data into training and testing sets: per-image or per-volume/subject splitting (Table 1). In the per-volume/subject splitting approach, the random selection of data for the testing set is done on the volumes (or subjects) ensuring that images from one volume (or subject) belong to either one of the training or testing sets. It is important to notice that even a per-volume split might not be enough to avoid overlap between the training and testing set. In fact, if multiple volumes are acquired from the same tissue region, the tissue structures will be very similar among the volumes. In such scenarios, a per-subject split is more appropriate. Overall, assuming that volumes are acquired from different tissue regions, splitting the dataset per-volume or per-subject (here called per-volume/subject) ensures that overlap between training and testing is not present. In the per-image approach, 2D images belonging to the same volume are considered independent: thus, the testing set is created by random selection from the pool of images without considering that images from the same volume (or subject) might end up in both the training and testing sets. Even if this approach clearly results in an overlap between the testing and training sets, several of reviewed studies as well as an earlier version of one of the most downloaded open-access OCT datasets employed a per-image split.
The aim of this study is to demonstrate the effect of improper dataset splitting (per-image) on model evaluation using three open-access OCT datasets, AIIMS14, Srinivasan’s16 and Kermany’s OCT2017 (version 2 and 3)15. These were selected among the other open-access datasets for several reasons: (1) they are examples of OCT medical images belonging to different medical disciplines (ophthalmology and breast oncology) and showing different tissue structures and textures, (2) they are used in literature to evaluate deep learning-based classification of OCT images, with Kermany’s dataset15 extensively used for developing deep learning methods in ophthalmology (over 14,500 downloads)17, and (3) the datasets are provided in two different ways, subject-wise for the AIIMS and Srinivasan’s datasets, and already split for both versions of the Kermany’s datasets. The latter is an important aspect to consider since many of the studies using Kermany’s version 2 dataset overlooked the overlap between the training and the testing data.
Results
LightOCT model classification performance on the three datasets and for the different dataset split strategies is summarized in Table 2, with results presented as mean ± standard deviation (m ± std) over the ten-times repeated five-fold cross validation. In addition, Fig. 2 shows the Matthews Correlation Coefficient (MCC) distribution as box plots. For all datasets, the per-image split strategy results in a higher model performance compared to the per-volume/subject strategy. Looking at both the AIIMS and Srinivasan’s datasets, a model trained using a per-image strategy had a higher mean MCC by 0.08 and 0.43, respectively, compared to the one trained on a per-volume/subject split. A similar trend can be seen for both versions of Kermany’s dataset, with an increase in mean MCC by 0.12 and 0.07 for version 2 and version 3, respectively, when shifting from a per-volume/subject to a per-image split strategy. Moreover, results on the original splits for both versions of Kermany’s dataset are higher compared to the corresponding per-volume/subject splits, with a difference in MCC of 0.30 and 0.04 for the version 2 and version 3 datasets, respectively.
Comparison between Matthews Correlation Coefficient for LightOCT model trained on different dataset split strategies. Each box plot summarizes the test MCC for the 50 models trained through a ten-times repeated five-fold cross validation. Results are presented for all the four datasets with the per-image split strategy shown in striped-green and per-volume/subject split strategy in dotted-orange. For Kermany’s datasets, the result of the models trained on the original_v2 and original_v3 splits are shown as full-black circle and full-black cross, respectively. Outliers are shown as diamond (♦).
Results on the random label experiments show that, for the original Kermany version 2 dataset, the obtained p-value was 0.071, with the high MCC for random labels indicating a probable data leakage. For the other datasets, the p-values were much larger. We conclude that using random labels during training can potentially be a way to automatically detect data leakage, but that it requires further research.
Discussion
Dataset split should be carefully designed to avoid overlap between training and testing sets. Table 1 summarizes several studies on deep learning applications for OCT data, specifying the described data split strategy. All the works using a per-image split strategy or the original split from both versions of Kermany’s dataset reported accuracies >95%. The results obtained on Kermany’s original_v2 split are in accordance with reported accuracy18,19,20, where the differences in performance can be attributed to the deep learning model used and its optimization. However, results on the third version of the dataset were much lower compared to those in literature10,21,22, even when using the same model architecture, loss and optimizer10. Interestingly, Table 1 also shows that studies using multiple datasets and reporting different split strategies for each dataset10,23,24, report as high accuracy on the per-volume/subject split datasets as the one on the original_v2 or the per-image split datasets. Moreover, the drop in MCC seen when using Kermany’s original_v2 compared to the original_v3 split, highlights the inflation effect that leakage between training and testing data has on model performance, especially when the original_v2 shows to have 92% overlap between training and testing sets while original_v3 has none. In the light of our results, it is reasonable to question whether the high performances reported for the per-volume/subject split datasets reflect the true high performance of the implemented methods, or are examples of inflated accuracy values due to data leakage between training and testing sets.
The difference in the effect of data leakage between datasets can be attributed to two reasons: (1) the way the dataset is provided for download and (2) the classification task that the model needs to learn. Firstly, Kermany’s dataset is provided already split in training, testing and validation sets (version 2 of the dataset), with overlap at both subject-ID level and at image level. Thus, using the original_v2 dataset as provided, highly inflates the model performance, with a drop in performance seen when using a per-image split (overlap only on a subject-ID level not on an image level) and an even larger decrease in the case of the appropriate split. AIIMS and Srinivasan’s datasets are provided with data from each subject saved independently, with split being performed in the reviewed studies using a per-image or per-subject/volume strategy (see Table 1). Thus, for these datasets the effect of inflation was measured with respect to the overlap in subject-IDs between the training and testing sets, and not with respect to having the exact same image in both sets. Disregarding the way the datasets are provided, the second reason for which the effect of data leakage was different between the datasets could be attributed to the difficulty of the classification task. Looking at the results for the proper split, the model performance on AIIMS dataset was higher compared to the one for Kermany’s dataset, suggesting that the binary classification between cancer and normal breast tissue was easier compared to the four-class classification for Kermany’s dataset. When improperly splitting the data, the advantage given to the model in classifying the test data by training on samples in the testing set had a smaller impact on AIIMS dataset than for Kermany’s since the classification task was easier. However, it is not trivial what task can be considered easy since this is influenced by a multitude of factors, including data, model architecture, and model optimization.
This study is limited in investigating only data leakage originating from the overlap between the training and testing sets. However, there are other sources of data leakage stemming from hyper-parameter optimization, data normalization, and data augmentation. During hyper-parameter optimization, model parameters as well as training strategies should not be tuned based on test performance. Similarly, in the case of data normalization, statistics such as mean and variance used for the normalization should only be computed on the training set, and not the entire dataset. Failing to do so results in biasing method design choices with information obtained from the testing set, thus compromising the evaluation of model generalization to new data. Finally, in leakage due to data augmentation, an image could be augmented multiple times, with its different augmented versions ending up in the training and testing set. This results in a data overlap similar to the one of a per-image split strategy, where images with the same structures and noise properties are in both training and testing sets. Both original splits in the Kermany and Srinivasan’s datasets are provided with images already augmented; however, overlap between training and testing with respect to data augmentation was not investigated in this work.
In conclusion, the dataset split strategy that is used can have a substantial impact on the evaluation of deep learning models. In this paper, it is demonstrated that, in OCT image classification applications specifically, a per-image split strategy of the volumetric data adopted by a considerable number of studies, returns over-optimistic results on model performance and an inflation of test performance values. This calls into question the reliability of the assessments and hindering an objective comparison between research outcomes. This problem has also been demonstrated in 3D magnetic resonance (MR) imaging studies13 and in digital pathology25, where data leakage between the training and testing sets resulted in over-optimistic classification accuracy (>29% slide level classification accuracy in MR studies and up to 41% higher accuracy in digital pathology). Moreover, greater attention should be paid to the structure of datasets made available to the research community to avoid biasing the evaluation of different methods and undermining the usefulness of open-access datasets. With the increased interest of the research community in the use of deep learning methods for OCT image analysis, this study intends to raise awareness on a trivial but overlooked problem that can spoil research efforts if not addressed correctly.
Methods
Dataset description
AIIMS dataset
The AIIMS dataset is a collection of 18480 2D OCT images of healthy (n = 9450) and cancerous (n = 9030) breast tissue14. The images are obtained from volumetric acquisitions and are provided as BMP files of size 245 × 442 pixels organized per-class and per-subject (22 cancer subjects and 23 healthy subjects).
Srinivasan’s dataset
The Srinivasan’s ophthalmology dataset16 collects a total of 3,231 2D OCT images of age-related macular degeneration (AMD), diabetic macular edema (DME), and normal subjects. For each class, data from 15 subjects is provided in independent folders. OCT images are given as TIFF files with 512 × 496 pixels saved after data augmentation (rotation and horizontal flip).
Kermany’s dataset
The Kermany’s ophthalmology dataset15,22 is one of the largest open-access ophthalmology datasets26 and is used by an extensive number of studies (see Table 1). The dataset contains images from 5319 patients (train = 4686, test = 633) for retina affected by choroidal neovascularization (CNV), diabetic macular edema (DME), and drusen as well as from normal retina. The dataset is available in different versions with version 2 and version 3 (latest) both used in literature. The difference between the dataset versions is threefold: (1) the total number of available images and their organization, (2) the number of images in the given testing set and (3) the extent of data overlap between the given training and testing sets. For both dataset versions, images are given as JPEG files of sizes ranging [384 to 1536] × [496 to 512] pixels saved after data augmentation (rotation and horizontal flip). The version 2 of the dataset is provided with splits for training (n = 83484 images), validation (n = 32 images), and testing sets (n = 968 images), with validation and testing sets balanced with respect to the classes. The version 3 of the dataset is given with training (n = 108312) and testing (n = 1000, balanced between the four classes). In this study, the given splits are referred to as original_v2 and original_v3 splits, for version 2 and version 3 of the dataset, respectively. For both versions of the dataset, there is no specification on if the split between sets is performed before or after data augmentation as well as if the split in training and testing sets was performed per-image or per-volume/subject. By performing an automatic check on the original_v2 split (assuming that the naming convention is CLASS_subject-ID_bscan-ID), it was found that 92% of the test images belong to subject-IDs also found in the training set. Moreover, by visually inspecting the given splits it was possible to identify images in the testing set that were similar to the training set (an example of such a case is training image = DRUSEN-8086850-6, testing image = DRUSEN-8086850-1). When performing the same automatic check on the original_v3 split, no overlap between subject-IDs was found. In Table 1 it is specified which version of Kermany’s dataset was used by the different studies. Among these, two studies used a mixture of both datasets23,27.
Dataset split
For all datasets, a custom split function was implemented to split the dataset per-image or per-volume. In either case, 1000 images from every class were assigned for testing in the case of Kermany’s and the AIIMS datasets. For the Srinivasan’s dataset, 250 images were selected for testing instead, given the smaller number of total images. Example images from AIIMS, Srinivasan’s and Kermany’s version 2 datasets are shown in Fig. 1b–d, respectively.
Model architecture and training strategy
The LightOCT model proposed by Butola et al.10 was used in this study. LightOCT is a custom, shallow and multi-purpose network for OCT image classification composed of a two-layer CNN encoder, and one fully connected layer with softmax activation as output layer. The first and second convolutional layers have 8 and 32 convolutional filters, respectively. The kernel size of the filters in both layers is set to 5 × 5 and the output of each layer passes through a ReLU activation function10. A max-pooling operation is present between the first and the second convolutional layer that cuts the spatial dimension of the output of the first layer in half. The two-dimensional output of the CNN encoder is then flattened to a one dimensional vector, which is fed to the fully connected layer for classification. The number of nodes in the fully connected layer is changed based on the number of classes specified by the classification task10.
For all of the classification tasks, the model was trained from scratch using stochastic gradient descent with momentum (m = 0.9) with a constant learning rate (lr = 0.0001). For all experiments, the batch size was set to 64 and the model was trained for 250 epochs without early stopping. Note that model architecture and training hyperparameters were not optimized for each dataset since it was out of the scope of this work. The model architecture as well as the training hyperparameters were chosen based on the results of Butola et al.10 The model and the training routine were implemented in Tensorflow 2.6.2, and training was run on a computer with a 20-core CPU and 4 NVIDIA Tesla V100 GPUs.
Evaluation metrics
Models were trained on the original splits, if available, and on training and testing splits obtained using a per-image and per-volume/subject strategy. A ten-times repeated five-fold cross validation was run for both split strategies to ensure reliability of the presented results28. A multi-class confusion matrix was used to evaluate the classification performance of the model with Matthews Correlation Coefficient (MCC) obtained as a derived metric coherent with respect to class imbalance and stable to label randomization29,30,31. Accuracy, precision, recall and F1-score were also derived for each class using the definitions provided by Sokolova et al.32 to allow comparison with previous studies. Additionally, receiver operator characteristic (ROC) curves were used along with the respective area under the curve (AUC). In an attempt to automatically detect bias due to data overlap, a random label experiment was carried out, where random labels were used for training a classifier and MCC was calculated on the test set (with original labels). To determine if the obtained MCC value was within the expected range, a null distribution was created for each dataset by creating 10000 test labels and prediction sets (also in this case random labels were used to simulate the random distribution) and calculating MCC for each of them. The MCC values obtained from the models trained using random labels on the different data splits (for which some have overlap) were compared to the respective null distribution (built without overlap) to calculate p-values using the one-sample Wilcoxon test (two-tailed).
Data availability
The datasets used in this study are open-access, with the AIIMS dataset14 available at https://www.bioailab.org/datasets, Srinivasan’s at https://people.duke.edu/~sf59/Srinivasan_BOE_2014_dataset.htm, Kermany’s OCT201715 version 2 at Mendeley33 https://data.mendeley.com/datasets/rscbjbr9sj/2 and version 3 also at Mendeley34 https://data.mendeley.com/datasets/rscbjbr9sj/3.
Code availability
The code used to generate the results in this paper is available at https://github.com/IulianEmilTampu/SPLIT_PROPERLY_OCT_DATA.git.
References
Xu, Y. & Goodacre, R. On Splitting Training and Validation Set: A Comparative Study of Cross-Validation, Bootstrap and Systematic Sampling for Estimating the Generalization Performance of Supervised Learning. Journal of analysis and testing 2, 249–262 (2018).
Kuhn, M., et al. Applied predictive modeling, vol. 26 (Springer, 2013).
Guyon, I. et al. A scaling law for the validation-set training-set size ratio. AT&T Bell Laboratories 1 (1997).
Refaeilzadeh, P., Tang, L. & Liu, H. Cross-validation. Encyclopedia of database systems 5, 532–538 (2009).
Litjens, G. et al. A survey on deep learning in medical image analysis. Medical image analysis 42, 60–88 (2017).
Ker, J., Wang, L., Rao, J. & Lim, T. Deep Learning Applications in Medical Image Analysis. IEEE Access 6, 9375–9389 (2017).
Anwar, S. M. et al. Medical Image Analysis using Convolutional Neural Networks: A Review. Journal of medical systems 42, 1–13 (2018).
Maier-Hein, L. et al. Why rankings of biomedical image analysis competitions should be interpreted with care. Nature communications 9, 1–13 (2018).
Wang, H., Won, D. & Yoon, S. W. A deep separable neural network for human tissue identification in three-dimensional optical coherence tomography images. IISE Transactions on Healthcare Systems Engineering 9, 250–271 (2019).
Butola, A. et al. Deep learning architecture "LightOCT" for diagnostic decision support using optical coherence tomography images of biological samples. Biomedical Optics Express 11, 5017–5031 (2020).
Irmak, E. Multi-classification of brain tumor MRI images using deep convolutional neural network with fully optimized framework. Iranian Journal of Science and Technology, Transactions of Electrical Engineering 45, 1015–1036 (2021).
Sadad, T. et al. Brain tumor detection and multi-classification using advanced deep learning techniques. Microscopy Research and Technique 84, 1296–1308 (2021).
Yagis, E. et al. Effect of data leakage in brain MRI classification using 2D convolutional neural networks. Scientific reports 11, 1–13 (2021).
Butola, A. et al. Volumetric analysis of breast cancer tissues using machine learning and swept-source optical coherence tomography. Applied optics 58, A135–A141 (2019).
Kermany, D., Zhang, K. & Goldbaum, M. Large Dataset of Labeled Optical Coherence tomography (OCT) and Chest X-Ray images. Mendeley Data 3, 10–17632 (2018).
Srinivasan, P. P. et al. Fully automated detection of diabetic macular edema and dry age-related macular degeneration from optical coherence tomography images. Biomedical optics express 5, 3568–3577 (2014).
Retinal OCT Images (optical coherence tomography), https://kaggle.com/paultimothymooney/kermany2018 Accessed: 2022-02-10.
Najeeb, S. et al. Classification of retinal diseases from OCT scans using convolutional neural networks. In 2018 10th International Conference on Electrical and Computer Engineering (ICECE), 465–468 (IEEE, 2018).
Chen, Y.-M., Huang, W.-T., Ho, W.-H. & Tsai, J.-T. Classification of age-related macular degeneration using convolutional-neural-network-based transfer learning. BMC bioinformatics 22, 1–16 (2021).
Chetoui, M. & Akhloufi, M. A. Deep retinal diseases detection and explainability using OCT images. In International Conference on Image Analysis and Recognition, 358–366 (Springer, 2020).
Latha, V., Ashok, L. & Sreeni, K. Automated Macular Disease Detection using Retinal Optical Coherence Tomography images by Fusion of Deep Learning Networks. In 2021 National Conference on Communications (NCC), 1–6 (IEEE, 2021).
Kermany, D. S. et al. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell 172, 1122–1131 (2018).
Kamran, S. A., Saha, S., Sabbir, A. S. & Tavakkoli, A. Optic-Net: A Novel Convolutional Neural Network for Diagnosis of Retinal Diseases from Optical Tomography Images. In 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA), 964–971 (IEEE, 2019).
Thomas, A. et al. A novel multiscale and multipath convolutional neural network based age-related macular degeneration detection using OCT images. Computer Methods and Programs in Biomedicine 209, 106294 (2021).
Bussola, N., Marcolini, A., Maggio, V., Jurman, G. & Furlanello, C. AI slipping on tiles: Data leakage in digital pathology. In International Conference on Pattern Recognition, 167–182 (Springer, 2021).
Khan, S. M. et al. A global review of publicly available datasets for ophthalmological imaging: barriers to access, usability, and generalisability. The Lancet Digital Health 3, e51–e66 (2021).
Tsuji, T. et al. Classification of optical coherence tomography images using a capsule network. BMC ophthalmology 20, 1–9 (2020).
Consortium, M. et al. The microarray quality control (maqc)-ii study of common practices for the development and validation of microarray-based predictive models. Nature biotechnology 28, 827 (2010).
Jurman, G., Riccadonna, S. & Furlanello, C. A comparison of mcc and cen error measures in multi-class prediction. PLOS ON (2012).
Chicco, D. & Jurman, G. The advantages of the matthews correlation coefficient (mcc) over f1 score and accuracy in binary classification evaluation. BMC genomics 21, 1–13 (2020).
Chicco, D., Tötsch, N. & Jurman, G. The matthews correlation coefficient (mcc) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation. BioData mining 14, 1–22 (2021).
Sokolova, M. & Lapalme, G. A systematic analysis of performance measures for classification tasks. Information processing & management 45, 427–437 (2009).
Kermany, D., Zhang, K. & Goldbaum, M. Labeled Optical Coherence Tomography (OCT) and Chest X-Ray Images for Classification, Mendeley, https://doi.org/10.17632/RSCBJBR9SJ.2 (2018).
Kermany, D., Zhang, K. & Goldbaum, M. Large Dataset of Labeled Optical Coherence Tomography (OCT) and Chest X-Ray Images, Mendeley, https://doi.org/10.17632/RSCBJBR9SJ.3 (2018).
Micko, A. et al. Diagnosis of pituitary adenoma biopsies by ultrahigh resolution optical coherence tomography using neuronal networks. Frontiers in Endocrinology 1345 (2021).
Athanasiou, L. S., Olender, M. L., José, M., Ben-Assa, E. & Edelman, E. R. A deep learning approach to classify atherosclerosis using intracoronary optical coherence tomography. In Medical Imaging 2019: Computer-Aided Diagnosis, vol. 10950, 163–170 (SPIE, 2019).
Wang, C. et al. Deep-learning-aided forward optical coherence tomography endoscope for percutaneous nephrostomy guidance. Biomedical optics express 12, 2404–2418 (2021).
Gesperger, J. et al. Improved diagnostic imaging of brain tumors by multimodal microscopy and deep learning. Cancers 12, 1806 (2020).
Saratxaga, C. L. et al. Characterization of Optical Coherence Tomography Images for Colon Lesion Differentiation under Deep Learning. Applied Sciences 11, 3119 (2021).
Singla, N., Dubey, K. & Srivastava, V. Automated assessment of breast cancer margin in optical coherence tomography images via pretrained convolutional neural network. Journal of biophotonics 12, e201800255 (2019).
Rasti, R., Rabbani, H., Mehridehnavi, A. & Hajizadeh, F. Macular OCT classification using a multi-scale convolutional neural network ensemble. IEEE transactions on medical imaging 37, 1024–1034 (2017).
Farsiu, S. et al. Quantitative classification of eyes with and without intermediate age-related macular degeneration using optical coherence tomography. Ophthalmology 121, 162–172 (2014).
Karimian, N., Salehi, H. S., Mahdian, M., Alnajjar, H. & Tadinada, A. Deep learning classifier with optical coherence tomography images for early dental caries detection. In Lasers in Dentistry XXIV, vol. 10473, 1047304 (International Society for Optics and Photonics, 2018).
Wang, R. et al. OCT image quality evaluation based on deep and shallow features fusion network. In 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), 1561–1564 (IEEE, 2020).
Acknowledgements
The study was supported by the grants from Åke Wiberg Stiftelse (M19-0455, M20-0034, M21-0083), FORSS - 931466, Vinnova project 2017-02447 via Medtech4Health and Analytic Imaging Diagnostics Arena (1908), Swedish research council (2018-05250) and ITEA/VINNOVA funded project ASSIST (2021-01954).
Funding
Open access funding provided by Linköping University.
Author information
Authors and Affiliations
Contributions
I.E.T. contributed with conceptualization, methodology, code development and implementation, formal analysis and drafting the manuscript. A.E. contributed with supervision and hardware resources. N.H.H. contributed with conceptualization, supervision and funding. All authors contributed to the interpretation of the results, have revised and edited the manuscript and approved the submitted version.
Corresponding author
Ethics declarations
Competing interests
AE has previously received NVIDIA hardware for research.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tampu, I.E., Eklund, A. & Haj-Hosseini, N. Inflation of test accuracy due to data leakage in deep learning-based classification of OCT images. Sci Data 9, 580 (2022). https://doi.org/10.1038/s41597-022-01618-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-022-01618-6
This article is cited by
-
Efficacy of MRI data harmonization in the age of machine learning: a multicenter study across 36 datasets
Scientific Data (2024)
-
AI chatbots show promise but limitations on UK medical exam questions: a comparative performance study
Scientific Reports (2024)
-
Non-endoscopic Applications of Machine Learning in Gastric Cancer: A Systematic Review
Journal of Gastrointestinal Cancer (2024)