Abstract
Evolutionary studies of cooperation in traditional human societies suggest that helping family and responding in kind when helped are the primary mechanisms for informally distributing resources vital to day-to-day survival (e.g., food, knowledge, money, childcare). However, these studies generally rely on forms of regression analysis that disregard complex interdependences between aid, resulting in the implicit assumption that kinship and reciprocity drive the emergence of entire networks of supportive social bonds. Here I evaluate this assumption using individual-oriented simulations of network formation (i.e., Stochastic Actor-Oriented Models). Specifically, I test standard predictions of cooperation derived from the evolutionary theories of kin selection and reciprocal altruism alongside well-established sociological predictions around the self-organisation of asymmetric relationships. Simulations are calibrated to exceptional public data on genetic relatedness and the provision of tangible aid amongst all 108 adult residents of a village of indigenous horticulturalists in Nicaragua (11,556 ordered dyads). Results indicate that relatedness and reciprocity are markedly less important to whom one helps compared to the supra-dyadic arrangement of the tangible aid network itself.
Similar content being viewed by others
Introduction
Human evolutionary research has historically conceptualised social support as a purely dyadic phenomenon (e.g., see Refs. 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16). That is, given some trait pertaining to two persons i and j — e.g., their genetic relatedness, history of helping each other, physical proximity, or difference in wealth — does i help j? Both elegant and tractable, this dyad-centric view of social support evokes classic theoretical models of cooperation as a “Prisoner’s Dilemma” within a void consisting only of ego (i) and alter (j)17. Yet it also belies the fact that aid relationships (i.e., who helps who) constitute complex networks of supportive social bonds that emanate throughout entire human communities.
Members of such networks may, in principle, unilaterally help whomever they wish. And their decisions to help — or to not help — specific others comprise a dynamic, supra-dyadic relational context that shapes one’s plausible set of aid targets at the micro level18,19,20,21,22. Put simply, in social support networks, aid is targeted and interdependent across dyads such that the patterning of cooperation among multiple alters jointly affects whom any one network member helps. This sociocentric (i.e., whole network) view of social support is distinct from the perspective taken by evolutionary graph theorists who study the emergence of cooperation on network structure and other spatial substrates (e.g., square grids) that may be fixed or dynamic (e.g., see Refs. 23,24,25). And it is distinct from the perspective taken by analysts of egocentric (i.e., personal) networks who study how the arrangement of intimate relationships exclusively between one’s closest contacts (e.g., the extent to which one’s friends are also friends) eases access to help (e.g., see Martí, Bolíbar, and Lozares26).
Differences between the dyad-centric and the sociocentric perspectives on social support are not merely cosmetic. Indeed, the dyad-centric stance of human evolutionary research has led to a situation wherein the relational context of helping behaviour is underexplored. And this has, in turn, impaired understanding of the relative importance of fundamental evolutionary mechanisms to the structuring of cooperative relationships in human communities.
Specifically, human evolutionary research on helping behaviour generally takes the theories of kin selection and reciprocal altruism as lodestars. In so doing, sociometric data from subsistence societies across the globe have been used to investigate whether consanguinity (i.e., genetic kinship) and reciprocity govern aid unconditionally and in relation to multiple social and demographic factors. These include affinity (i.e., marriage-based kinship), physical proximity, relative need, homophily (e.g., based on age and gender), social closeness, friendship, religiosity, reputation, conflict, status, and anthropometric measurements such as size, height, and strength. And, on balance, evidence1,2,3,4,5,6,7,8,9,10,13,14,16,27,28,29,30,31,32,33 suggests that helping family and responding in kind when helped are the primary mechanisms by which humans informally distribute resources vital to day-to-day survival (e.g., advice, information, food, money, durables, and physical assistance).
However, despite laudable exceptions2,7,15,28,29,30,31,32,33,34 and perhaps due to the influence of methodological trends in the wider behavioural ecology literature on relationships between animals (see Refs. 35,36,37), human evolutionary studies of real helping behaviour have typically relied on non-network methods — namely, monadic regression, dyadic regression, and permutation tests (e.g., see Refs. 1,2,3,5,6,8,9,10,11,12,13,14,16,27). Respectively, these techniques treat the supra-dyadic structure of social support networks as ignorable, reducible to dyads, or a nuisance to be corrected for38. Yet, sociocentric research by sociologists39,40,41,42,43,44,45,46,47,48,49 firmly establishes that humans create and maintain relationships in accordance with factors intrinsic to the supra-dyadic arrangement of network structure itself (e.g., processes of degree-reinforcement and group formation involving at least three persons). And this sociological research makes clear that network-structure-related dynamics can operate simultaneously and independently of non-network factors (e.g., age and kinship).
Ultimately, reliance on methods that disregard complex interdependences between aid obscures the extent to which helping family and responding in kind when helped outrank the dynamics of the cooperative system within which decisions to assist specific individuals take place. This uncertainty represents a substantial gap in our scientific understanding of altruism. Accordingly, here I tackle a major point of interest in evolutionary anthropology and human behavioural ecology50 specifically through the lens of the sociology of social networks18,21,51, asking:
RQ: How important is helping family and responding in kind when helped relative to supra-dyadic, network-structure-related constraints on the provision of aid?
The Current Study
To answer my research question, I use Koster’s27 recently-released cross-sectional data on genetic relatedness and the habitual provision of tangible aid (e.g., firewood, food, valuable items, and/or physical assistance). Re-analysed here due to their exceptional detail and measurement quality in addition to their broad relevance to the scientific community (see Methods), these data were collected in 2013 and concern a complete population. Specifically, they cover all 108 adult (18+) residents (11,556 ordered dyads) of the 32 households of Arang Dak — a remote village of 279 indigenous Mayangna and Miskito swidden (i.e., “slash-and-burn”) horticulturalists. Arang Dak sits on the Lakus River in Nicaragua’s Bosawás Biosphere Reserve, a neotropical forest in the Department of Jinotega.
In total, the tangible aid network that I analyse — i.e., x(t2013)— consists of 1,485 asymmetric aid relationships between the adult residents of Arang Dak. Of the 1,485 aid relationships, 1,422 are verified by the source and the recipient of help. That is, xij(t2013) = 1 if villager i reported in 2013 that they give tangible aid to villager j at least once per month and villager j reported in 2013 that they receive tangible aid from villager i at least once per month. Still, note that Koster’s27 data document self-reported resource flows as opposed to observed transfers. Named sources and targets of aid are based on the village roster — not freely recalled from memory. See Methods for a summary of the data and details on the measurement of the network and kinship.
Modelling Strategy
To analyse tangible aid in relation to supra-dyadic network structure (Fig. 1), I use generative network models following Redhead and von Rueden32 and von Rueden et al.33, amongst other human evolutionary scientists2,7,15,28,29,30,31,32,33,34. Specially, I rely on Stochastic Actor-Oriented Models (SAOMs) which are used for observational (i.e., non-causal) analyses of the temporal evolution of networks.
Put simply, SAOMs are akin to multinomial logistic regression. More formally, SAOMs are simulations of individual network members’ choices between outgoing relationships with different rewards and costs. These simulations are calibrated or “tuned” to the observed network data. That is, conditional on x (i.e., the observed states of a dynamic network), SAOMs simulate network evolution between successive observations or “snapshots” of the network at \(M\) discrete time points — i.e., \(x\left({t}_{m}\right)\to x\left({t}_{m+1}\right)\) — as a continuous-time, Markovian process of repeated, asynchronous, and sequential tie changes. The Markovian process is defined on the space of all possible directed graphs for a set of N = {1, …, n} network members40,42,44,52,53,54,55.
SAOMs decompose change between successive network observations into its smallest possible unit. Specifically, “change” means creating one outgoing tie if it does not exist, dropping one outgoing tie if it does, or doing nothing (i.e., maintaining the status quo network). More formally, during a SAOM simulation, focal actors i (ego) myopically modify just one of their outgoing relationships with some alter j in the set of network members N (i.e., j ∈ N, j ≠ i). The change made by i is the change that maximises a utility or “evaluation” function. In this respect, the evaluation function captures the “attractiveness”44 of tie changes — where “attraction” means “…something like ‘sending a tie to [an actor j] with a higher probability if all other circumstances are equal.’” (Snijders and Lomi56, p. 5).
The evaluation function itself is a weighted sum of parameter estimates \(\widehat{\beta }\) and their associated covariates k (i.e., SAOM “effects”44) plus a Gumbel-distributed variable used to capture random influences55. The simulated tie changes or “ministeps”44 made by i shift the network between adjacent (unobserved) states. These states differ, at most, by the presence/absence of a single tie40,42. And the probabilities of the ministeps — a large number of which are required to bring one observation of the network to the next (i.e., \(x\left({t}_{m}\right)\to x\left({t}_{m+1}\right)\)) — are given by a multinomial logit which uses the evaluation function as the linear predictor.
Each covariate k used to specify the evaluation function summarises some structural (i.e., purely network-related) feature or non-structural feature of i’s immediate (i.e., local) network — e.g., the sum of the in-degrees of i’s alters, the number of reciprocated dyads that i is embedded in, or i’s number of outgoing ties weighted by genetic relatedness. These features correspond to theoretical mechanisms of interest (e.g., preferential attachment, reciprocal altruism, or kin selection) and generally take the form of unstandardised sums.
SAOM parameter estimates \(\widehat{\beta }\) (log odds ratios) summarise the association between the covariates and the simulated tie changes or “ministeps”. Specifically, should a focal actor i have the opportunity to make a ministep in departure from some current (i.e., status-quo) network state x in transit to a new network state x±ij — i.e., the adjacent network defined by i’s addition/subtraction of the tie xij to/from x — \({\widehat{\beta }}_{k}\) is the log odds of choosing between two different versions of x±ij in relation to some covariate k. For example, \({\widehat{\beta }}_{{\rm{Reciprocity}}}=1.7\) would indicate that the log odds of i creating and maintaining the supportive relation xij is, conditional on the other covariates k, larger by 1.7 when xij reciprocates a tie (i.e., xji) compared to when xij does not reciprocate a tie (i.e., reciprocated ties are more “attractive”). In contrast, \({\widehat{\beta }}_{{\rm{Reciprocity}}}=-1.7\) would indicate that the log odds of xij is, conditional on the other effects, smaller by −1.7 when xij reciprocates a tie compared to when xij does not reciprocate a tie (i.e., reciprocated ties are less “attractive”).
Given the longitudinal nature of the model, the gain in the evaluation function for a ministep is determined by the difference Δ in the value of the statistic s for a covariate k — i.e., Δk,ij(x, x±ij) = sk,i(x±ij) − sk,i(x) — incurred through the addition/subtraction of xij to/from x (see Block et al.42 and Ripley et al.44 on “change statistics”). Accordingly, \({\widehat{\beta }}_{{\rm{Reciprocity}}}=1.7\), for example, is the value that xij positively contributes to the evaluation function when xij increases the network statistic sk,i(x) underlying the Reciprocity effect by the value of one (i.e., ΔReciprocity,ij (x, x±ij) = sReciprocity,i(x±ij) − sReciprocity,i (x) = 1 − 0 = 1).
The probabilities of network members being selected for a ministep is governed by a separate “rate” function. And the baseline rate parameter λ is a kind of intercept for the amount of network change between successive observations of the analysed network. Larger baseline rates indicate that, on average, more simulated tie changes were made to bring one observation of the network to the next (i.e., \(x\left({t}_{m}\right)\to x\left({t}_{m+1}\right)\)).
However, as the data from Nicaragua are from a single point in time (i.e., 2013), I use the cross-sectional or stationary Stochastic Actor-Oriented Model (cf. von Rueden et al.33). Accordingly, Arang Dak’s tangible aid network is assumed to be in “short-term dynamic equilibrium.” As Snijders and Steglich40 (p. 265) discuss in detail, “this ‘short-term equilibrium’ specification of the SAOM is achieved by requiring that the observed network is both the centre and the starting value of a longitudinal network evolution process in which the number of change opportunities per actor [i.e., λ] is fixed to some high (but not too high) value.”
Practically speaking, this means that the cross-sectionally observed network is used as the beginning and the target state for a SAOM simulation — i.e., \(x\left({t}_{2013}\right)\to x\left({t}_{2013}\right)\) — during which actors are allowed to make, on average, very many changes (i.e., λ) to their portfolio of outgoing ties. These simulated tie changes produce a distribution of synthetic networks with properties that are, on average, similar to those of the cross-sectionally observed network in a converged SAOM — where the target properties correspond to the researcher-chosen SAOM effects k. Put simply, “[cross-sectional] SAOMs assume that the network structure, although changing, is in a stochastically stable state.” (Krause, Huisman, and Snijders57, p. 36–37). Thus, the estimated parameters \(\widehat{\beta }\) continue to summarise the rules by which ministeps unfold. However, the asynchronous, sequential, simulated tie changes, in a sense, “cancel out” and thus hold the network in “short-term dynamic equilibrium”40,42. Formally, the cross-sectional SAOM is defined as a stationary distribution of a Markov Chain with transition probabilities given by the multinomial logit used to model change between adjacent network states40,42.
The rate parameter λ is fixed at 36 for my analysis. The value of 36 is the maximum observed out-degree in the source-recipient-verified tangible aid network x(t2013). Accordingly, under λ = 36, all members of the tangible aid network have, on average, at least one opportunity to modify their entire portfolio of outgoing ties during the simulations. Nevertheless, to ensure the robustness of my results, I also fit a second set of models for which λ was fixed to 108 (i.e., thrice the maximum out-degree).
Model Specification
To assess the importance of kinship and reciprocity to hypothetical decisions to help others (i.e., ministeps), I use four archetypal specifications of the SAOM’s evaluation function. These model specifications feature nested sets of covariates (i.e., the SAOM “effects”44). And, using language found in prior evolutionary studies3,5, I refer to these archetypal specifications as the “Conventional Model” (Model 1) of aid, the “Extended Model” (Model 2) of aid, the “Networked Aid Model (Limited)” (Model 3), and the “Networked Aid Model (Comprehensive)” (Model 4).
The first specification (i.e., Model 1) comes from Hackman et al.3 and Kasper and Borgerhoff Mulder5 who respectively label it the “Human Behavioural Ecology” and “Conventional” model. This specification is comprised of just four dyadic covariates — one each for consanguinity (i.e., Wright’s coefficient of genetic relatedness), affinity (i.e., Wright’s coefficient of genetic relatedness between i’s spouse s and his/her blood relative j), the receipt of aid, and geographic distance. The first three covariates are used to test long-standing predictions of helping in order to reap indirect and direct fitness benefits in line with the theories of kin selection and reciprocal altruism (see Refs. 1,5,27,58,59 for primers). And the fourth covariate is used to adjust for tolerated scrounging — i.e., what Jaeggi and Gurven4 (p. 2) define as aid resulting from one’s inability to monopolise resources due to costs imposed by the resource-poor — where a covariate for distance operationalises pressure to help imposed by those who are spatially close4.
The second specification (i.e., Model 2) reflects Kasper and Borgerhoff Mulder’s5 and Thomas et al.’s9 extensions to the conventional model (see also Page et al.16). Specifically, and following important work by Allen-Arave, Gurven, and Hill1, Hooper et al.14, and Nolin7, it is distinguished by nuanced tests of kin selection and reciprocal altruism via interactions between: (i) consanguinity and the receipt of aid; (ii) consanguinity and relative need; and (iii) consanguinity and geographic distance. Furthermore, Kasper and Borgerhoff Mulder’s5 and Thomas et al.’s9 extended model includes covariates for the non-network-related attributes of individuals (e.g., gender, wealth, and physical size), thus adjusting for homophily, trait-based popularity, trait-based activity, and local context (e.g., results from a gift-giving game9 or, in the present case, infidelity and discrimination based on skin-tone27).
The third specification (i.e., Model 4) is my revision of the second. It is geared to make the relational context of aid explicit. This is done using nine covariates that account for the breadth of sociologists’ contemporary understanding of supra-dyadic interdependence between positive-valence (i.e., not based on disliking or aggression), asymmetric social relationships39,40,41,42,43,44,45,46,47,48,49. In keeping with the nature of the SAOM, each of these covariates summarises some structural feature of a villager’s immediate (i.e., local) network (e.g., the number of transitive triads that she is embedded in). Accordingly, each structural covariate is used to capture a form of self-organisation — i.e., network formation driven by an individual’s selection of alters in response to network structure itself (Lusher et al.49, p. 10–11 and 23–27).
Specifically, the covariates added in the third specification reflect predictions derived from three fundamental sociological theories of the emergence of non-romantic relationships. The first is structural balance theory which posits that individuals create and maintain ties that move groups of three people from an intransitive to a transitive state (i.e., transitive closure), the latter of which is understood to be more psychologically harmonious or “balanced” (see Refs. 39,43,47,48,60,61,62 for primers). The second is Simmelian tie theory which posits that, once formed, individuals will maintain relationships embedded in maximally-cohesive groups of three people such that 3-cliques (i.e., fully-reciprocated triads) are resistant to dissolution (see Refs. 43,48,63 for primers). The third is social exchange theory (as it relates to structured reciprocity) which posits that individuals will unilaterally give benefits to others in response to benefits received such that indirect reciprocity (i.e., returns to generosity) and generalised reciprocity (i.e. paying-it-forward) in groups of three people encourage cyclic closure — i.e., the simplest form of chain-generalised exchange (see Refs. 19,20,43 for primers). Furthermore, the third specification reflects the broad prediction that individuals vary in their propensity to send and receive relationships based on their structural position alone (e.g., popularity-biased attachment) leading to dispersion in the distribution of in-degrees and out-degrees (see Refs. 39,44,49 for primers) — especially for ties with an inherent cost to their maintenance39,42.
Last, I consider a fourth specification (i.e., Model 3) that uses a subset of the nine network-structure-related covariates included in Model 4. This limited set of structural effects typifies the specifications used in prior human evolutionary studies of empirical help that present generative models of entire networks2,7,15,28,29,30,31,32,33,34. Specifically, the fourth specification features just three network-structure-related covariates to account for structural balance theory, self-reinforcing in-degree (i.e., popularity-bias), and the interplay between in-degree and out-degree.
Descriptive statistics for the relevant attributes of the 108 residents of Arang Dak appear in Table 1. Formulae used to calculate the network statistics sk,i(x) underlying each effect k used to specify my SAOMs, alongside verbal descriptions to aid reader interpretation, appear in Online-Only Table 1. See Methods for additional rationale behind the third specification.
Model Comparison
Compared to prior human evolutionary research on social support networks, I take two novel approaches to gauging the importance of kinship and reciprocity to help. First, I use a technique41 specifically designed to measure the relative importance of individual effects in SAOMs (see Methods). And second, I evaluate each specification’s ability to produce synthetic graphs with topologies representative of the structure of the analysed tangible aid network64.
Judging model specifications using topological properties reflects one of the core purposes of methods such as the SAOM and the Exponential Random Graph Model (ERGM) — i.e., to explain the emergence of global network structure (see Refs. 40,42,46,47,49 also Refs. 18,48), not simply the state of individual dyads (i.e., is aid given or not?). Admittedly, explaining global network structure is not a stated primary aim of dyadic-centric or sociocentric studies of help by human evolutionary scientists, including those wherein authors rely on SAOMs or ERGMs2,7,15,28,29,30,31,32,33,34. Still, topological reproduction is an important, strong test of the relative quality of the four archetypal specifications as each encodes the set of rules presumed to govern network members’ decisions about whom to help.
To clarify, recall that here it is assumed, a priori, that network members can, in principle, cooperate with whomever they wish, that their cooperative decisions are intertwined across multiple scales, and that their micro-level decisions ultimately give rise to macro-level patterns of supportive social bonds (see Refs. 18,19,20,21,22). The macro-level patterns generated by SAOMs and ERGMs can differ dramatically based on specification40,46,47,49,64,65. Thus, the empirical relevance of a candidate model rests with its ability to produce synthetic graphs similar to the observed structure40,42,46,47,48,49,64. Ultimately, divergence between the real and simulated graphs suggests that a candidate specification is suspect as it does not describe how some network of interest could have formed.
Results
Parameter estimates \(\widehat{\beta }\) (associational; non-causal) from the Conventional and Extended Models, as well as estimates from the limited and comprehensive versions of the Networked Aid Model, appear in Table 2 and Table 3. Note well that results are for cross-sectional SAOMs40,42. Thus, estimates relate to a simulation of sequential tie changes wherein network members have, on average, a large, fixed number of opportunities (i.e., λ) to modify their portfolio of outgoing relationships. Again, this simulation is “tuned” to the single observation of Arang Dak’s tangible aid network x(t2013), where the cross-sectionally observed network is represented by a probability distribution in the form of a stationary distribution of a dynamic interaction process that is Markovian (Snijders and Steglich40, p. 224 and 243; Block et al.42, p. 208–209). Put alternatively, “…correspondence between the [SAOM] and [the] single-observed network is specified by considering…model parameters for which the observed [network] is in a short-term dynamic equilibrium” (Snijders and Steglich40, p. 243). Recall that the rate parameter λ is fixed at 36 (Table 2). However, results are robust to a sizeable increase of λ to 108 (Table 3).
For brevity, I only discuss Table 2. And to assist readers, pictograms (“→”) indicating the arrangement of aid relationships (i.e., who helps who) between individuals (e.g., i, j, h, etc.) in the various scenarios captured by the network-structure-related effects are used to discuss the estimates throughout the Results section. For example, a complete (i.e., a “Simmelian” or “dense”) triad is indicated by \(\left[i\rightleftarrows h\rightleftarrows j\rightleftarrows i\right]\). In pictograms such as this one, all of which correspond to the formulae in Online-Only Table 1, the focal actor — i.e., the individual whose decision to aid another network member is being modelled by the SAOM (hence, “actor-oriented”) — is always labelled “i”.
Robust evidence of aid in line with kinship, reciprocity, and proximity
Regardless of model, and conditional on the other effects, estimates suggest that the log odds of creating and maintain an aid relationship xij is positively associated with: (i) being helped (Reciprocity); (ii) living in close proximity (Geographic Distance); and (iii) being related — whether by blood (Consanguineal Relatedness), marriage (Affinal Relatedness), or choice (Godparental Relation). There is no compelling evidence to suggest need-based transfers (Relative Wealth Rank). And evidence of a negative interaction between relatedness and reciprocity in Model 2 (\({\widehat{\beta }}_{{\rm{Consanguineal}}{\rm{Relatedness}}\times {\rm{Reciprocity}}}=-1.288\), se = 0.407, p = 0.002) and Model 3 (\({\widehat{\beta }}_{{\rm{Consanguineal}}{\rm{Relatedness}}\times {\rm{Reciprocity}}}=-1.180\), se = 0.420, p = 0.005) disappears after the inclusion of the remaining network-structure-related effects in Model 4 (\({\widehat{\beta }}_{{\rm{Consanguineal}}{\rm{Relatedness}}\times {\rm{Reciprocity}}}=-0.675\), se = 0.428, p = 0.115). Moreover, Model 2, Model 3, and Model 4 provide no compelling evidence of interactions between need and kinship (Consanguineal Relatedness × Relative Wealth Rank; i.e., kin-directed altruism) or distance and kinship (Consanguineal Relatedness × Geographic Distance).
Clear evidence of aid in line with manifold supra-dyadic dynamics
There is strong observational evidence of simple transitivity in Model 3 (\({\widehat{\beta }}_{{\rm{Transitive}}{\rm{Triplets}}}=0.090\), \(se=0.006\), \(p < 0.001\)) and Model 4 (\({\widehat{\beta }}_{{\rm{Transitive}}{\rm{Triplets}}}=0.320\), \(se=0.021\), \(p < 0.001\)). Of course, transitive triads may be a by-product of unobserved homophilous preferences and unobserved opportunities for interaction (see Rivera et al.39, p. 105–107, and Stadtfeld et al.47). Still, conditional on the five homophily effects and proximity, both Model 3 and Model 4 indicate that the log odds of creating and maintaining an aid relationship xij is positively associated with the presence of (i) indirect aid to j via third parties (i.e., a tendency for \(i\to j\) in the transitive triad \(\left[i\to h\to j\leftarrow i\right]\)); and (ii) shared targets of aid (i.e., a tendency for \(i\to j\) in the transitive triad \(\left[i\to j\to h\leftarrow i\right]\)). This is expected given published results from generative models of social support networks in subsistence populations28,29,30,31,32,33,34. However, Model 4, which features a more comprehensive set of network-structure-related effects compared to prior evolutionary work, indicates the operation of group dynamics over and above simple transitivity, net of simple reciprocity, homophily, proximity, and kinship.
Specifically, and in line with important research by Block43, Model 4 provides strong observational evidence of a negative interaction between transitivity and reciprocity (i.e., a tendency against \(i\to j\) in the triad \(\left[i\to h\to j\rightleftarrows i\right]\); \({\widehat{\beta }}_{{\rm{Transitive}}{\rm{Reciprocated}}{\rm{Triplets}}}=-0.338\), se = 0.049, p < 0.001). This suggest that weak ties with third parties may help stabilise the asymmetric provision of aid43. Concurrently, there is weak evidence to suggest that residents engage in simple chain-generalised exchange19,20 (\({\widehat{\beta }}_{{\rm{Three}}{\rm{Cycles}}}=0.069\), se = 0.035, p = 0.051). That is, Model 4 indicates that the log odds of creating and maintaining an aid relationship xij is positively associated with i’s indirect receipt of support from j (i.e., a tendency for \(i\to j\) in the cyclic triad \(\left[i\leftarrow h\leftarrow j\leftarrow i\right]\)).
Moreover, there is strong evidence to suggest helping across household boundaries (\({\widehat{\beta }}_{{\rm{Transitive}}{\rm{Triplets}}{\rm{Jumping}}{\rm{HHs}}}=\) \(0.105\), se = 0.035, p = 0.003). That is, conditional on the other effects, mixed-household two-paths \([{i}_{{\rm{HH}}-1}\to \) \({h}_{{\rm{HH}}-1}\to {j}_{{\rm{HH}}-2}]\) are positively associated with the log odds of creating and maintaining the inter-household tie \({i}_{{\rm{HH}}-1}\to {j}_{{\rm{HH}}-2}\). Thus, coresidents who help one another appear to converge on aid targets outside of their home (i.e., \(\left[{i}_{{\rm{HH}}-1}\to {h}_{{\rm{HH}}-1}\to {j}_{{\rm{HH}}-2}\leftarrow {i}_{H{\rm{H-}}1}\right]\)). This dynamic has been linked to the maintenance of intra-household harmony in prior evolutionary work27.
Further still, Model 4 points to the existence of cohesive support groups (\({\widehat{\beta }}_{{\rm{Dense}}{\rm{Triads}}}=0.145\), se = 0.035, p < 0.001). More precisely, Model 4 provides strong observational evidence to suggest that the log odds of creating and maintaining an aid relationship xij is positively associated with the scenario wherein a focal resident i and an alter j from whom i receives aid both exchange resources with a third villager h (i.e., a tendency for \(i\to j\) in the 3-clique \(\left[i\rightleftarrows h\rightleftarrows j\rightleftarrows i\right]\)). That said, Simmelian tie theory in its classic form does not posit that individuals actively create complete triads43,48, only that ties in complete triads are resistant to dissolution once formed. Thus, without longitudinal data to clarify, it is unclear to what extent the positive Dense Triads effect reflects the maintenance of old aid ties versus an impetus to begin helping others in line with the third-party integrative pressure intrinsic to Simmelian groups48,63.
Crucially, a proper interpretation of results from generative network models considers structural effects jointly. This is because they relate to the emergence of sub-graphs that are generally nested like matryoshki (i.e., “Russian Dolls”). For example, a single complete triad \(\left[i\rightleftarrows h\rightleftarrows j\rightleftarrows i\right]\) is comprised of three reciprocated dyads, six transitive triplets, six transitive reciprocated triplets, two three cycles, and two possible inter-household transitive triplets. Thus, the signs of the “lower-order” effects in Model 4 concern the establishment of sub-graphs over and above those nested within complete triads. Accordingly, the estimates — i.e., positive Dense Triads alongside positive Transitive Triplets, negative Transitive Reciprocated Triplets, and positive Three Cycles — collectively suggest a preponderance of weakly-connected groups outside of maximally-connected regions of the tangible aid network which, in the present case, appears to help facilitate macro-level system integration (see Fig. 1).
Kinship and tangle aid in Arang Dak. Each arc (i.e., directed relationship) indicates the provision of tangible aid by some villager i to some other villager j (108 villagers; 1,485 arcs). Arcs are coloured to reflect whether the source and target of aid are “close kin” (i.e., consanguineal relatedness or affinal relatedness ≥ 0.125). Red arcs emanate from spouses (i.e., affinal relatedness = 1.0). Dark-blue arcs emanate from primary kin — i.e., relatives with a consanguineal or affinal relatedness equal to 0.5 (e.g., full-siblings, parent and child, wife and brother-in-law, husband and mother-in-law). Lighter-blue arcs and green arcs emanate from near kin (i.e., 0.375 ≥ consanguineal/affinal relatedness ≥ 0.125). And yellow arcs emanate from kin who are not close — either genetically or through marriage (i.e., consanguineal/affinal relatedness < 0.125) — or emanate from residents of Arang Dak who are not related (i.e., consanguineal/affinal relatedness = 0). See also “Rationale for Network Diagram Construction” in Methods.
As for degree-based dynamics, there is strong evidence to suggest that, conditional on the other effects, the log odds of creating and maintaining an aid relationship xij is negatively associated with the out-degree (i.e., activity) of j in Model 3 (\({\widehat{\beta }}_{{\rm{Out-degree}}{\rm{Popularity}}}=-0.071\), se = 0.009, p < 0.001) and Model 4 (\({\widehat{\beta }}_{{\rm{Out-degree}}{\rm{Popularity}}}=-0.043\), se = 0.014, p = 0.003). Put alternatively, there is a tendency against indirect reciprocity (i.e., \(i\to j\) in the two-path \(\left[i\to j\to h\right]\)) outside of transitive, cyclic, and dense triads. Furthermore, there is strong evidence to suggest that the log odds of creating and maintaining xij is positively associated with the in-degree (i.e., popularity) of j (i.e., a tendency for \(i\to j\) in the in-two-star \(\left[i\to j\leftarrow h\right]\)) in Model 3 (\({\widehat{\beta }}_{{\rm{In-degree}}{\rm{Popularity}}}=0.048\), \(se=0.008\), \(p < 0.001\)) and Model 4 (\({\widehat{\beta }}_{{\rm{In-degree}}{\rm{Popularity}}}=0.049\), se = 0.011, p < 0.001). However, like above, and in both Model 3 and Model 4, the positive In-degree Popularity effect indicates a preponderance of in-stars over and above those nested within transitive and dense triads and thus more-global returns on popularity (see Fig. 1).
That said, help in Arang Dak appears to be structured in a fashion whereby aid provision is not redundant across those in need. Specifically, the positive In-degree Popularity effect indicates a tendency for residents to receive aid by virtue of having many sources of support. However, the negative Shared Popularity effect strongly evidenced by Model 4 (\(\widehat{\beta }=-0.018\), se = 0.002, p < 0.001) indicates that, conditional on the other effects, the log odds of creating and maintaining an aid relationship xij is negatively associated with the scenario wherein i helps the same network members as one of j’s patrons h. Put alternatively, popular recipients of aid — who themselves may not help many others given the negative Out-degree Popularity effect — tend to have divergent donor pools (i.e., a tendency against \(i\to j\) in the tetrad \(\left[i\to j\leftarrow h\to k\leftarrow i\right]\); n.b., the nested in-two-stars centred on j and k).
Given new experimental findings concerning the Agta hunter-gatherers of the Philippines8, the signs of the three popularity effects perhaps jointly point to a kind of need-based transfer in a village characterised by wealth inequality27. That is, these results perhaps suggest that residents help those who, based on the concentrated altruism of others, are understood to lack sufficient means (Positive In-Degree Popularity; Negative Shared-Popularity) as opposed to helping those who are understood to be in a position to give based on their level of patronage (Negative Out-degree Popularity; see also Smith et al.8 on alter cooperativeness and Macfarlan, Quinlan, and Remiker66 on levels of patronage and prosocial reputations).
Supra-dyadic dynamics prominently govern expected aid provision
The prior section concerns evidence for network-structure-related constraints on aid provision. This evidence is implicitly assumed to exist by my research question and was thus in need of confirmation. I now turn to values of Ik(x) — i.e., the relative importance of each effect k under each of the four models — which appear in Table 4. Recalling the multinomial logit underlying each SAOM, Ik(x, i) is the proportional contribution of the kth effect to the distribution of the probabilities of each possible change to one’s portfolio of outgoing ties that an actor i could make in departure from the observed state of the analysed network x (i.e., x(t2013)) given the SAOM-specific parameter estimates \(\widehat{\beta }\) corresponding to the set of researcher-chosen effects k41. And Ik(x) is simply the average of the actor-specific proportional contributions Ik(x,i) across all N members of network x. Put alternatively, Ik(x) is the global expected influence of the kth effect over the relational decisions of residents of Arang Dak in the hypothetical scenario wherein they are presented with the opportunity to modify the observed state of the network x by changing a single tie (see Methods for a more technical definition of Ik(x, i)).
Values of Ik(x) for Model 1 (i.e., the Conventional Model) and Model 2 (i.e., the Extended Model) are in line with what one would expect a priori and based on: (i) previous evolutionary studies of supportive relationships in traditional human populations;1,3,5,6,7,8,9,13,14,27,28,29,30,31,32,33,34 and (ii) a recent meta-analysis of food sharing amongst human and non-human primates4. That is, under Model 1 and Model 2, Consanguineal Relatedness and Reciprocity, alongside Geographic Distance, appear to hold substantial sway over who residents of Arang Dak are expected to provide tangible support to. More importantly, however, is that when Model 2 is expanded to include network-structure-related constraints on alter choice in Model 3 and Model 4 (i.e., the Networked Aid Models), the relative importance of these three effects to aid provision wanes sharply. And, under Model 3 and Model 4, the effects used to capture supra-dyadic interdependence, particularly those related to popularity and non-covariate-based transitivity, are roughly as influential and, in some cases, markedly more influential than Consanguineal Relatedness, Affinal Relatedness, Reciprocity, and Geographic Distance — where interactions between Consanguineal Relatedness and Reciprocity, Relative Wealth Rank, and Geographic Distance are marginal.
Accordingly, to the extent that the signs of the network-structure-related effects in Tables 2 and 3 reflect a kind of systemic need-based aid and a willingness to establish loose-knit cooperative groups outside of one’s immediate support-clique, values of Ik(x) suggest that these dynamics are the most salient to aid provision and thus the emergence of the tangible support network spanning Arang Dak. Nevertheless, recall that Ik(x) is a proportion. Consequently, it is reasonable to expect to observe some shrinkage of each share of influence as the size of a SAOM specification grows. And, despite this shrinkage, Reciprocity remains one of the most influential effects whilst eclipsing Consanguineal Relatedness — a result that is in line with findings from evolutionary studies by, for example, Allen-Arave et al.1, Jaeggi and Gurven4, Kasper and Borgerhoff Mulder5, and Nolin7.
Supra-dyadic dynamics are critical to system emergence
Values of Ik(x) do not reveal which archetypal specification makes a “good” model of Arang Dak’s tangible aid network — i.e., a model that reproduces fundamental topological features of the observed structure18,40,46,47,49. As mentioned above, judging relative model quality in this manner is crucial as I wish to assess the determinants of aid in relation to the global cooperative system within which help is embedded. In this respect, Model 3 and Model 4 are not superfluous.
Specifically, consider results from tests64 of the joint Mahalanobis distance (MHD) between the components of distributions comprised of features of the real aid network (e.g., the number of residents with an in-degree = 0, 1, 2, etc.) and the average of these same features across 20,000 synthetic networks simulated under each model (Table 2; bottom). As Fig. 1 indicates, aid relationships in Arang Dak cohere to form very rich global structure. Thus, I gauge model quality using a diverse set of aggregated micro- and macro-level network features40,49. Namely, I focus on: (i) the distributions of the in-degrees, the out-degrees, and the geodesic distances (i.e., shortest paths); alongside (ii) the triad census (i.e., the frequencies of each of the 16 possible non-isomorphic sub-graphs of three villagers); and (iii) the clique census (i.e., the frequencies of each inclusion-maximal, completely-connected sub-graph of size w appearing in the observed aid network). Furthermore, for a topic-specific test, I consider: (iv) the distribution of the number of aid relationships amongst each observed type of consanguineal relative (i.e., coefficient of genetic relatedness = 0.5 (parent/child; full siblings), 0.25 (grandparent/grandchild), 0.125 (first cousins), …, 0.00390625 (third cousins)).
Of course, one can expect models that ignore self-organisation to perform poorly vis-à-vis the reproduction of global network structure. Accordingly, what is interesting here is precisely how poorly do structure-agnostic models perform relative to a model that accounts for complex interdependences. Keeping this in mind and comparing joint Mahalanobis distances within the set of four tests associated with each of the six distributions (Table 2; bottom), Model 3 and Model 4 are clearly superior to Model 1 and Model 2 — both of which fail to generate plausible graphs given what was observed in Arang Dak by wide margins.
Model 3, which typifies specifications used in prior evolutionary studies of social support featuring generative network models, is an improvement over Model 1 and Model 2. Still, Model 3 fails to reproduce the Triad Census. Thus, Model 3 is suspect and inferior to Model 4 despite Model 3 capturing the distribution of in-degrees, out-degrees, geodesic distances, cliques, and consanguineous ties. Note that the relatively large joint Mahalanobis distances associated with the fit of Model 1 are unsurprising as its specification is anaemic. However, the inadequacy of Model 2 is interesting given its inclusion of effects for kinship, physical proximity, trait-based activity, trait-based popularity, and homophily as these effects could, in principle, induce supra-dyadic structure alone (see Refs. 39,47,61,62).
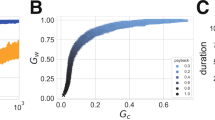
SAOMs have no single figure for model selection that is equivalent to the AIC/BIC. However, one may consider the global degree of certainty RH — i.e., Snijders’44,67 Shannon-entropy-based measure of explained variation. RH is the network (i.e., global) average of the actor-specific predictability of which other network member a focal actor i is expected to choose as an alter in departure from the state of the observed network x under a fitted SAOM. RH ranges from zero to one — where zero indicates complete uncertainty (i.e., a uniform probability distribution for the potential alter choices) and one indicates complete certainty (i.e., one network member has all probability mass for a given choice). However, in practice, RH will be low given the high variability of chosen alters and the difficulty of predicting precisely which dyads will have ties present given the stochastic nature of the actor-oriented model44,67. With that in mind, RH for Model 1, Model 2, Model 3, and Model 4 are, respectively, 0.154, 0.166, 0.180, and 0.214. This is further evidence that Model 4 is an improvement over Model 1, Model 2, and Model 3.
Finally, the χ2 test statistic for the multi-parameter Wald test of whether the effects added in Model 4 over those in Model 3 are all simultaneously equal to zero is 151.56 (df = 6; p < 0.005). And the χ2 test statistic for the multi-parameter Wald test of whether the effects added in Model 3 over those in Model 2 are all simultaneously equal to zero is 268.07 (df = 3; p < 0.005). This is further evidence that tangible aid in Arang Dak is associated with network-structure-related dynamics beyond simple reciprocity that operate over and above preferences for helping kin.
Discussion
Compared to other animals, the extent to which humans cooperate, particularly with unrelated individuals, “defies biological expectation” and is “unique in its degree and its scope” (Voorhees, Read and Gabora68, p. 194). Consequently, clarifying who we choose to cooperate with and why — especially in naturalistic scenarios — is a major scientific task.
Explicitly adopting a sociological and sociocentric perspective, here I have tried to add to our evolutionary understanding of human cooperation by using simulations of network dynamics to analyse exceptional public data on genetic kinship and tangible aid across an entire population of adult horticulturalists. In so doing, I have provided clear, quantitative evidence around the relative importance of competing mechanisms of cooperation in a setting significant to our evolutionary past69. Specifically, my results indicate that relatedness and reciprocity are markedly less important to whom one helps compared to sociological dynamics intrinsic to the arrangement of the network of tangible aid itself — particularly those related to popularity-biased attachment and pure transitivity. Furthermore, my results indicate that the set of covariates typically used to explain helping behaviour vis-à-vis evolutionary theory constitute models that are incapable of generating synthetic networks with fundamental topological properties similar to those of the real tangible aid graph. Ultimately, and perhaps controversially, my findings suggest that prior evolutionary work on helping behaviour in traditional human societies may overestimate the roles of kinship and reciprocity due to overlooking several appreciable aspects of the self-organisation of social support. Thus, my findings bolster the validity of evolutionary scientists’ attempts to move beyond common, dyad-centric predictions of why humans assist each other by emphasising supra-dyadic network dynamics (e.g., see Refs. 27,28,29,30,31,32,33,34 and Gurven and Kraft’s response to Ready and Power31, p. 88–89, in addition to Hamilton et al.70). Yet my findings also suggest that these attempts, while laudable, have not gone far enough due to a narrow focus on simple transitivity.
Accordingly, evolutionary sociocentric research (cf. experiments8,71) intended to uncover the principal determinants of social support in traditional human societies should explicitly and comprehensively account for supra-dyadic network structure in order to accurately gauge the relative importance of kinship and reciprocity to helping behaviour. This is especially so for scholars relying on the SAOM and the ERGM as we currently lack extensive knowledge about the behaviour of estimates from these models when network-structure-related covariates are omitted and, as a result, network dependencies are ignored or incompletely represented (see especially Refs. 40,42,43,46,47,49,61,64,65 on the central importance of the specification of SAOMs and ERGMs).
Of course, additional studies are needed to ascertain the replicability of my findings and their generalisability to social support in other settings relevant to our evolutionary history. That said, the apportioning of salience seen here is unlikely to be universal. Indeed, in a prior study45 building on an ecological theory of network formation72, I used 162 village-specific SAOMs of friendship between rice farmers in China to show that actor-specific relative importance scores Ik(x,i) can systematically vary across individuals’ physical environments — namely, Ik(x,i) for the effects Reciprocity, Transitive Triplets, and Three Cycles. Additionally, the results I have presented here may be overdetermined by socioecological factors unique to Arang Dak.
Specifically, Amazonian horticulturalists have been found to have a higher group relatedness compared to, for example, hunter-gatherers69,73. Consequently, the general strength of genetic ties in communities like Arang Dak (avg. relatedness = 0.052) may itself fuel in-group cooperation73 and thus serve as a potent backdrop for the very rich global structure seen in Fig. 1 and, by extension, the network-structure-related dynamics evidenced by Tables 2 and 3 (see also Table 1 of Walker73, p. 385, and Table 1 of Koster et al.74, p. 3, to compare relatedness amongst the Mayangna and Miskito to groups in different societies). Along this line, and speculatively speaking, the higher group relatedness in Arang Dak may then depress the relative importance of consanguinity as the distinction between close and distant/non-kin becomes less relevant to any one decision about whom to help, possibly explaining the very low values of Ik(x) for Consanguineal Relatedness and Affinal Relatedness in Model 3 and Model 4 compared to the values of Ik(x) for network-structure-related effects such as In-Degree Popularity, Transitive Triplets, and Shared Popularity. Furthermore, at the time of data collection (i.e., 2013), all residents of Arang Dak were Catholic27. And, as Power29 demonstrates, religious identity can also fuel a preponderance of cooperative relationships within groups of individuals who might not otherwise be connected. Therefore, the richness of the tangible aid network and the heightened salience of the network-structure-related effects may in part stem from Arang Dak’s religious homogeneity and, as 85% of adult residents were Mayangna at the time of data collection, its ethnic homogeneity (see also Voorhees et al.68 on shared identity and the evolution of cooperation).
These characteristics of Arang Dak present an important scope condition with respect to the replicability and generalisability of my results — i.e., societies with lower group relatedness, more religious heterogeneity, and/or more ethnic heterogeneity may see network dynamics play a less prominent role in directing help. Such a possibility underscores the need for scrutiny of my observational findings through systematic comparative analyses of network formation from a socioecological perspective. And future evolutionary sociocentric research should explore fluctuation in the relative importance of kinship and reciprocity vis-à-vis other features of human communities that stand to shape cooperation such as size45, wealth inequality and market integration5,31,75,76,77, predominant subsistence style45,78, dispersal norm28,71, and descent rule6.
As for the weaknesses of my study, limitations include an inability to adjust SAOMs for: (i) intra-village friendship (i.e., a major conduit of social support3,79,80,81); and (ii) constraints on access to potential patrons beyond geographic proximity82. Furthermore, my focus on just one type of social support in the form of tangible aid (c.f., provision of practical knowledge15,34,78) is not ideal. Yet, the most severe shortcoming of my study rests with its cross-sectional design. This is because social relationships, and thus the relative importance of network dynamics, are unlikely to be static41,51,60 — especially in subsistence populations where resource access can be highly stochastic (see Kaplan et al.83). Accordingly, my results — which, recall, reflect the assumption that the analysed network is in short-term dynamic equilibrium — may not hold over long timescales. Given this uncertainty around temporality, future evolutionary sociocentric research should make a special effort to emulate Redhead and von Rueden32,33 who fit SAOMs to data on tangible aid relationships amongst Amazonian forager-horticulturalists over an eight-year period.
Finally, I conclude with two major points. First, I stress that the network-structure-related dynamics evidenced by Tables 2 and 3 are not reducible to simple reciprocity. Nor are they precluded from predominantly, or even exclusively, unfolding within sub-regions of a social support network composed entirely of close kin1,7,14,16,28,31 — i.e., those individuals for whom the indirect fitness benefits of cooperation will be highest and direct fitness benefits easier to realise to the extent that family members are predisposed to “trust one another, interact frequently, and rarely defect on their repayment” (Allen-Arave et al.1, p. 314–315). For example, although I found no evidence of kin-favoured reciprocity, a qualitative reading of Fig. 1 plainly indicates that cliquish sub-graphs of varying sizes saturated with close kin (i.e., consanguineal/affinal relatedness ≥ 0.125) are likely to underlie the positive and somewhat influential Dense Triads effect — itself a type of structurally-embedded reciprocation48,63. Similarly, Fig. 1 suggests that the positive and powerful In-degree Popularity and Transitive Triplets effects are at least partially underpinned at the more-local level by the 1,111 aid relationships emanating from close kin. In contrast, the other 374 aid relationships emanating from distant-kin and non-kin likely drive the more-global returns on popularity and the less-local clustering responsible for the macro-level system integration mentioned above (see also Migliano et al.84 on non-kin dyads and the integration of Agta hunter-gatherer communities). Put formally, and using the traditional three-digit M-A-N (Mutual-Asymmetric-Null) Triad classification scheme, 81% (664/820) of the observed complete triads (i.e., \(\left[i\rightleftarrows k\rightleftarrows j\rightleftarrows i\right]\); M-A-N Code “300”) and 62% (623/999) of the semi-complete triads (i.e., \(\left[i\rightleftarrows k\rightleftarrows j\to i\right]\); M-A-N Code “210”) are composed entirely of close kin. Yet just 39% (73/186) of the observed transitive triads (i.e., \(\left[i\to k\to j\leftarrow i\right]\); M-A-N Code “030-T”) and 35% (314/897) of the in-two-stars (i.e., \(\left[i\to j\leftarrow k\right]\); M-A-N Code “021-UP”) are composed entirely of close kin.
Second, it is important to state plainly that this article is not meant to be antagonistic. Specifically, I do not wish to imply that the study of cooperative mechanisms of historic interest to evolutionary scientists should be abandoned in favour of an exclusive focus on supra-dyadic network dynamics. Instead, integration of sociological and evolutionary theories of sociality has far greater scientific potential (e.g., see Tokita and Tarnita85) — where a major strength of the formalist study of networks within the tradition of mathematical sociology86 is that it is highly ecumenical. That is, scholars in this area broadly take the evidence-based view that the emergence of non-romantic social relationships in human groups is multi-mechanistic and, necessarily, multi-theoretical. Practically speaking, this implies that narrow theoretical models are unlikely to explain global network structure along several key dimensions (e.g., geodesics, triadic morphology, degree connectivity, etc.) and thus alter choice in supra-dyadic context (see Refs. 18,39,40,42,43,46,47,48,49,51,61,64,72,81,87 for key discussions and examples of the explanatory leverage gained via a multi-mechanistic, multi-theoretical logic).
Sceptical readers closely aligned with the evolutionary sciences may retort that being ecumenical makes the sociological study of network formation “theoretically weak” — especially in light of the elegance, strength, and trans-species relevance of predictions derived from the theories of kin selection and reciprocal altruism alone. Nevertheless, being ecumenical does not equate to being non-theoretical86,87 and worthy of dismissal. Again, the network-structure-related dynamics discussed here are rooted in established lines of sociological research around structural balance theory, Simmelian tie theory, social exchange theory, and structural position (see Refs. 19,20,39,43,47,48,49,60,61,62,63,72,81,86,87,88). This research has proved influential as formalist network thinking has percolated from sociology to the social and natural sciences more broadly. And this research — especially the strand on triads and their ability to modulate conflict — undergirds nascent, exciting evolutionary theorising around the adaptive (i.e., fitness-enhancing) value of indirect connections for humans, non-human primates, and non-human animals (see Refs. 27,89,90,91,92,93 as well as Ilany et al.94,95). Accordingly, fusion of sociological and evolutionary research strikes me as the most promising means of future theorisation and empirical investigation of the dynamics of entire social support networks to the extent that the arrangement of these systems encodes, or even fosters33, cooperation-relevant information that individuals can perceive and act upon.
Essential to this integrative effort will be the SAOM and the ERGM — two methods uniquely poised for multi-mechanistic analyses of cooperation due to their broad accessibility, high degree of flexibility, and explicit emphasis on interdependence across multiple scales. Of course, neither model is unimpeachable. Indeed, the SAOM is limited by its stylisation of individual behaviour (see Snijders55 on myopia) and the ERGM by challenges around difficult data-model combinations (see Schweinberger et al.65 on degeneracy) — where both models are computationally expensive and still under development with respect to statistical theory42,52,54,65. Furthermore, the intensive nature of ethnographic fieldwork — particularly for the purposes of carrying out sociometric censuses of entire subsistence populations96,97 — may make amassing the amount of data needed to achieve good statistical power with these models difficult98. And, depending on the richness of the available network data (e.g., network size, number of ties), field researchers may need to pay extra attention to model specification. Thus, the full version of the “Network Aid” model could be inappropriate, contingent on one’s inability to achieve model convergence with such a complex specification relative to one’s ability to achieve excellent convergence and good model fit with a more parsimonious set of effects.
Still, SAOMs and ERGMs are promising tools for carrying out unified relational analyses wherein researchers simultaneously test sociological and evolutionary predictions of cooperation with varying degrees of overlap40,42,47,49,65 — an analytic scenario that more-traditional, non-network methods may struggle with (e.g., see Getty’s response to Gurven99, p. 563–564). Here, I have focused narrowly on predictions derived from the theories of kin selection, reciprocal altruism, and tolerated scrounging following pioneering human evolutionary research on social support1,2,3,4,5,6,7,8,9,10,13,14,16,27,28,29,30,31,32,33. However, there are other evolutionary theories of cooperation that are relevant to explaining helping behaviour. And avenues for further exploration via sociocentric analysis and with the aid of generative network models and longitudinal data include long-term reciprocity4,8,14,19,20, by-product mutualism99, and partner choice7,8,31,75,100.
Methods
Data summary
Data from Nicaragua were collected in 2013 by Koster27 who released them to the public in 2018. Koster27 provides substantial supplementary ethnographic information (e.g., on wealth as a proxy for need). Here it suffices to say that Koster’s27 data on social support are especially apt for answering my research question despite being cross-sectional and concerning just one category of aid in a single village. This is due to their exceptional detail and top-quality measurement relative to data used in prior published research on social support in traditional human societies. Koster’s27 data are also remarkable when contrasted with the data used in research on face-to-face human social networks in advanced economies (e.g., adolescent friendship networks in school classrooms).
Specifically, the sociometric data are comprehensively annotated with information on villagers’: (i) attributes (i.e., age, gender, ethnicity, skin tone, BMI, and household wealth); (ii) familial ties (i.e., consanguineal, affinal, and social kinship); and (iii) spatial location (i.e., household membership and inter-household distance). Furthermore, several aspects of the reports on aid provision themselves make for unusually comprehensive relational data.
First, aid reports cover an entire adult population — not just household heads, “household representatives”, spouses, or men. Second, aid reports are not artificially censored at common cut-offs (e.g., up to 5–10 nominations). Third, aid reports are from a roster-based recognition task — not free recall — where the names on the roster were randomly presented during the sociometric interviews. Fourth, aid reports are double-sampled — i.e., the villagers reported who they habitually received tangible aid of some form from and who they habitually provided tangible aid of some form to. Fifth, aid reports were collected at the individual level — not the household level — and thus they avoid the problematic premise that households are homogenous entities that establish social ties in a unitary fashion96. These data-collection decisions are significant as they help mitigate measurement error which can seriously undermine network-based research101.
Based on my recent review of social and biomedical scientists’ measurement of face-to-face networks spanning villages in low- and middle-income countries96, and to the best of my knowledge of data releases in the intervening period, no other publicly available, annotated sociometric data on tangible aid of such a high quality exists. Accordingly, Koster’s27 data from Arang Dak are more than apt for my analysis. Indeed, they are appropriate for wide reuse across the scientific community à la Wayne W. Zachary’s102 classic “Karate Club” network data. This is especially so given the great difficulty of collecting face-to-face sociometric data97 (cf. Twitter data) concerning adults (cf. children in schools) and the relative rarity of public data on offline social networks in developing nations103 compared to, for example, western, educated, industrialised, rich, and democratic (WEIRD104) societies (e.g., the United States, the Netherlands).
For instance, Koster’s27 data are extremely relevant to: (i) sociologists and psychologists interested in modelling voluntary relationships26,79,80; (ii) ecologists and zoologists interested in contrasting social interaction across species4,105; (iii) physicists and computer scientists interested in identifying universal principles by comparing social networks to technological and biological networks106; and (iv) economists interested in the networks of the rural poor107. That said, those interested in re-using Koster’s27 dataset should note that it lacks key pieces of information in the form of variables for social closeness and friendship3,79,80,81. And note once again that Koster’s27 dataset is cross-sectional. Nevertheless, these two shortcomings are strongly counterbalanced by the dataset’s richness.
To learn more about life in Arang Dak and the Miskito and Mayangna, see Koster and colleagues27,69,73,74,108,109,110,111.
Network measurement
To measure social support, permutations of a single question focused on tangible aid were used. Specifically, Koster27 (p. 6) asked: “Who provides tangible support to you at least once per month?” — where respondents were prompted with relevant examples of aid received such as firewood, food, valuable items (e.g., canoes), and help with physical tasks. Respondents were also asked the inverse. That is, villagers were invited to nominate those to whom they gave tangible support at least once per month.
In total, villagers reported 2,595 “support receiving” ties and 2,958 “support giving” ties. However, the binary, square sociomatrix x(t2013) representing the tangible aid network that I use to fit my SAOMs was constructed to reflect habitual resource transfer based on residents’ mutual assent (i.e., double confirmation). That is, xij(t2013) = 1 if villager i reported giving tangible aid to villager j at least once per month and villager j reported receiving tangible aid from villager i at least once per month. x(t2013) was constructed in this manner in order to mitigate measurement error in line with authoritative sociological research on respondent accuracy101 (see also Ready and Power112 for an alternative perspective). In total, mutual assent yields 1,422 source-recipient-verified aid relationships (n.b., the product-moment graph correlation between the matrices constructed using either the reports of the receiver or the giver of aid is 0.360).
Two villagers were away during data collection. They did not provide aid reports but could be nominated by their fellow villagers. To avoid missingness, I coded ties to/from these two villagers as present/absent in line with the unilateral reports of the other 106 residents (see also Lyle and Smith12 for a similar approach), where the two possible ties between the two absent villagers were coded as absent. Accordingly, in total, x(t2013) is comprised of 1,485 asymmetric tangible aid relationships (graph density = 0.129; graph reciprocity [i.e., the proportion of arcs that are reciprocated] = 0.712; graph transitivity [weak rule] = 0.381; mean out-/in-degree = 13.75; standard deviation of out-degrees = 7.688; standard deviation of in-degrees = 7.782).
Kinship measurement
Genealogical interviews were used to derive Wright’s coefficient of genetic relatedness (i.e., consanguineal relatedness) for each pair of residents i and j as well as the binary dyadic indicator for infidelity relations between households, the latter of which reflects information on illegitimate children. Koster27 (p. 10) emphasises that the use of genealogies is an appropriate proxy for genetic similarity in Arang Dak as individuals frequently disperse during early adulthood such that the population is well-mixed. Note that two residents i and j may have both a consanguineal and an affinal relation (e.g., a mother’s blood tie to her child and her affinal tie to her child via her husband). To account for this, Koster27 coded affinal relatedness (i.e., Wright’s coefficient of relatedness between resident i’s spouse s and resident j) as zero unless affinal relatedness is greater than or equal to twice the value of consanguineal relatedness for the dyad of interest. As Koster27 recounts, this coding decision is ethnographically valid as it reflects perceptions of kinship in Arang Dak which give primacy to marriage-based ties in the absence of stronger blood relations. In the case of multiple third-party affinal ties between i and j, affinal relatedness reflects the strongest.
Stochastic Actor-Oriented Models versus Exponential Random Graph Models
Although it has only recently been detailed40,42, the cross-sectional SAOM is used here instead of the more-widely used Exponential Random Graph Model (ERGM)42,46,49 for two reasons. First, the SAOM has a direct measure of relative importance41 (discussed below). And second, the SAOM explicitly links choice between competing relationships with different rewards and costs42 to a scenario wherein network members’ selection of alters comprises an ever-changing, multilevel relational context for decision making18,19,20,21,22.
Like ERGMs, cross-sectional SAOMs provide insight into the self-organisation that could have given rise to the observed network despite the absence of longitudinal data — where the cross-sectionally observed network is assumed to possess traces of generative mechanisms unfolding through time (see Lusher et al.49, p.17–19). Along this line, the assumption of short-term dynamic equilibrium one must make to fit a cross-sectional SAOM is not radically different from that which is commonly made when using the standard (i.e., cross-sectional) ERGM. Specifically, should one use parameter estimates from an ERGM to draw micro-level conclusions about the relational behaviour of network members — e.g., interpreting the estimate for reciprocity as a bias/tendency for actors to begin/continue to respond in kind — one is forced to assume that the analysed network is in an equilibrium state (see Block et al.53, p. 183–182, for a discussion). Nevertheless, I used SAOMs due to the two reasons above.
Note that unlike the ERGM, degeneracy is generally understood to not be an issue with the cross-sectional SAOM as long as the rate parameter λ is fixed at a reasonable value (see Snijders and Steglich40, p. 243 and 265). Practically speaking, problems with degeneracy are expected for values of λ on the order of 10,000 or greater (see Snijders and Steglich40, p. 267).
Block et al.42 (p. 205–209) and Snijders and Steglich40 (p. 231–243) provide extensive formalism and extended details on the cross-sectional SAOM. Additionally, Block et al.42 compare cross-sectional SAOMs to ERGMs from first principles (see also Lusher et al.49, p. 130–140, and Schweinberger et al.65). For a comparison of the assumptions around temporality underlying SAOMs and ERGMs, see Block et al.53.
SAOM estimation settings
Cross-sectional SAOMs were fit using the R programming language and the algorithm SIENA (i.e., Simulation Investigation for Empirical Network Analysis)44 by following the coding directive of Snijders and Steglich40 which requires one to randomly and arbitrarily alter a single tie in the analysed sociomatrix x that is used as the target network state during the simulation. This change is simply to allow the SIENA algorithm to execute as the RSIENA R package does not yet have a dedicated option for fitting the cross-sectional SAOM.
For all models presented in Tables 2 and 3, the absolute value of the convergence t-ratio for each effect is less than 0.1. Furthermore, the overall convergence ratio for each model is less than 0.15. Results in Table 2 and Table 3 are rounded to the nearest thousandth for presentation and obtained using four sub-phases in estimation Phase 2 (parameter values) and 20,000 iterations in Phase 3 (standard errors, convergence checks, and goodness-of-fit). Readers unversed in the SIENA algorithm and the SAOM framework should see Ripley et al.44 for a detailed discussion of these convergence diagnostics and estimation settings which were chosen to be cautious.
The Indlekofer-Brandes measure of relative importance for SAOM effects
Formally, and as summarised in my prior work (see Simpson45, p. 113), the measure of Indlekofer and Brandes41 may be outlined as follows. For some villager i that has the opportunity to amend her portfolio of outgoing relations by changing a single tie variable and all other villagers h′ in the network x, let \(\widehat{\beta }\) represent a set of SAOM parameter estimates that correspond to β — i.e., the set of effects k of length L used to specify the SAOM’s aforementioned utility function. Furthermore, and recalling the multinomial logit at the heart of the SAOM, let πi represent the probability distribution implied by \(\widehat{\beta }\) that assigns to each of i’s potential alters j ∈ h′ a value πi(j) — i.e., the probability that i will change the value of her tie variable with j by creating a tie if it does not exist or dropping a tie if it exists; all depending on the state of the network x — such that \({\sum }_{j=1}^{h{\prime} }{\pi }_{i}\left(j\right)=1\). For some effect k∈β, its importance is defined to be the sum of the absolute values of the pointwise differences between πi and \({\pi }_{i}^{(-k)}\), the latter of which is implied by \(\widehat{\beta }\) when only sk,i(x) — i.e., the actor-specific network statistic si for some effect k (i.e., the local-network features; e.g., see Online-Only Table 1) — is set to zero. As such, k’s importance is its direct contribution to πi according to \(\widehat{\beta }\) given x and thus its expected impact on i’s inferred relational decision (i.e., with whom will i modify a tie?).
This formulation of “importance” is distinct from: (i) the magnitude of the estimated log odds ratio \({\widehat{\beta }}_{k}\) for an effect k; (ii) the “statistical significance” of \({\widehat{\beta }}_{k}\); and (iii) the unstandardised network statistic sk,i(x) associated with \({\widehat{\beta }}_{k}\). Specifically, construction of k’s importance is akin to assessing the amount of change in a dependent variable (here, modulation of πi) associated with a change in some independent variable (i.e., setting sk,i(x) equal to zero). Moreover, by setting sk,i(x) equal to zero for a given actor i — as opposed to excluding the parameter βk from a given SAOM — the complete model specification, the magnitude of parameter estimates, and the correlations between effects (as manifest in the set of estimated parameters \(\widehat{\beta }\)) are all respected. This would not be the case were βk to be dropped and a SAOM re-estimated (see Indlekofer and Brandes41, p. 300–301).
Moreover, the impact of k on the relational decision of villager i given the state of the network x, or Ik(x,i), is relative as k’s importance is normalised using the sum of the expected importance of all effects in β in order to reflect k’s proportional contribution to πi such that \(\mathop{\sum }\limits_{k=1}^{L}{I}_{k}(x,i)=1\). Thus, Ik(x,i), and, by extension, its global average Ik(x), may be compared within and across models. This is not equivalent to comparison of the magnitude of the log odds ratios \(\widehat{\beta }\) which can be misleading — something clearly demonstrated in Table 2, Table 3, and Table 4 when contrasting values of Ik(x) and the magnitude of the estimates \(\widehat{\beta }\) within and across the models. As network change is simulated (i.e., unobserved), Ik(x,i) and, by extension, Ik(x) are based on the observed state of the analysed network (i.e., x(t2013)).
Readers are directed to Indlekofer and Brandes41 who provide extensive logic and additional formalism for their measure. However, two points merit mention here. First, comparing values of Ik(x) within and across models is valid and my usage of Ik(x) for this research is in line with the original application of the measure (see Indlekofer and Brandes41, p. 295–297). And second, a major shortcoming of the measure of Indlekofer and Brandes41 is that it is not designed to account for uncertainty of the estimated parameters \(\widehat{\beta }\). That is, Ik(x,i) only reflects the parameter estimates (irrespective of their standard errors), the model specification, and the observed state of the network. These limitations are not ideal. However, no other measure for the relative importance of effects in SAOMs exists at the time of writing.
Last, values of Ik(x) in Table 4 — as well as the other values reported in Table 2 and in Table 3 — are exactly reproduceable across SAOM re-estimations when: (i) using the model specifications in Table 2/Table 3; (ii) using the tangible aid network as defined above; (iii) carrying out estimation using a single computing core (i.e., no parallel processing); and (iv) using the same random seed (see Ripley et al.44, p. 62, as well as the R code for this paper on GitHub). This is because values of Ik(x) are derived after the simulation-based estimation of a given SAOM is complete. Note that estimation using a specific random seed and a single computing core are both required to ensure that results are invariant across re-estimations of the same SAOM (see Ripley et al.44 as well as the RSIENA source code for the function sienaRI() and the function sienaAlgorithmCreate()).
Incorporating relatedness and geographic distance into the SAOM specifications
How scholars adjust their models for consanguinity and affinity varies across the scientific literature. For example, Kasper and Borgerhoff Mulder5 and Nolin7 do not include a measure of affinity in their Conventional Models whereas Hackman et al.3 do. Furthermore, some scholars use “dummy” dyadic covariates for degrees of consanguineal relatedness and degrees of affinal relatedness separately (e.g., see Refs. 3,8,28) or in combination by creating a single binary dyadic covariate for “close kinship” (i.e., parent/child, siblings, spouses, parents-in-law, and siblings-in-law; e.g., see Refs. 29,30,31,32,33). Here, I strongly prefer parsimony, tractability, and maximum covariate information. Accordingly, “dummy” variables are avoided. And, as a result, consanguineal relatedness and affinal relatedness appear in their continuous form in all models, resulting in just two dyadic covariates. For other continuous implementations of relatedness, see Refs. 1,2,6,9,10,14,15,27. Following Preciado et al.113 and again preferring parsimony, I also included geographic distance (natural log transformation after adding a constant of one) in its continuous form in all SAOMs as opposed to using “dummy” dyadic covariates for degrees of proximity (e.g., see Hackman et al.3).
“Networked Aid” SAOM specification vis-à-vis prior evolutionary research
Self-organisation is a basic concern for sociologists of social networks18,40,42,46,47,49 and the comprehensive version of the Networked Aid Model includes eight structural effects to account for the breadth of sociological research on interdependence between positive-valence (i.e., not based on disliking or aggression), asymmetric social relationships (see Refs. 19,20,39,40,41,42,43,44,45,47,48,49,60,63,81,87,113,114,115 in addition to Refs. 46,61,72). These eight effects also regularly feature in empirical applications of the SAOM by the model’s architects40,41,42,43,44,47,52,81,113,114,115. And they capture: (i) responding in kind (Reciprocity); (ii) self-reinforcing popularity (In-Degree Popularity; i.e., the Matthew Effect/Preferential Attachment); (iii) self-reinforcing activity (Out-Degree Activity; i.e., the effect of cooperativeness on itself); (iv) the interplay between activity and popularity (Out-Degree Popularity); (v) transitive closure (Transitive Triplets); (vi) cyclic closure (Three Cycles); (vii) the interplay between reciprocity, transitive closure, and cyclic closure (Transitive Reciprocated Triplets); and (viii) the establishment of complete triads wherein all six asymmetric relationships are present (Dense Triads).
The comprehensive version of the Networked Aid Model also includes a special triadic effect (Transitive Triplets Jumping HHs) to capture the social organisation of whole human communities in line with structural balance theory vis-à-vis household membership (see Koster27). And it includes a special tetradic effect (Shared Popularity) to account for expected deviation from structural equivalence in helping behaviour (i.e., distinction between individuals’ egocentric networks of outgoing ties) within and across households (see Simpson96). Note that a minimally comprehensive (cf. simply “minimal”) set of triadic effects includes Transitive Triplets, Transitive Reciprocated Triplets, Three Cycles, and, possibly, Dense Triads given sociological scholarship on social exchange theory, structural balance theory, and Simmelian tie theory; where, again, Transitive Triplets Jumping HHs reflects the anthropological findings of Koster27 vis-à-vis structural balance theory.
To the best of my knowledge, Redhead and von Rueden32,33 introduced SAOMs to evolutionary anthropology and human behavioural ecology with their studies on tangible support amongst the Tsimané of Bolivia. Accordingly, my analysis is only the third application of SAOMs for the purposes of testing evolutionary predictions around the formation of cooperative relationships in traditional human societies (see also Snijders et al.114 who use SAOMs to investigate social support in seven Senegalese villages with no reference to evolutionary theory). That said, Redhead and von Rueden32,33 only analyse aid between men. Furthermore, out of the ten network-structure-related dynamics captured in my models, Redhead and von Rueden32,33 only tested for five — i.e., simple reciprocity, self-reinforcing popularity, shared popularity, self-reinforcing activity, and simple transitivity using the popular geometrically-weighted edgewise shared partners effect (see Ripley et al.44, p. 44–45, 128, and 131–134, on the gwespFF effect versus the broader Transitive Triplets effect).
On the other hand, and again to the best of my knowledge of published research broadly falling under the umbrella of “evolutionary anthropology and human behavioural ecology”, Exponential Random Graph Models have been used by human evolutionary scientists at least since Nolin’s7 2011 analysis of food sharing amongst the Lamaholot of Indonesia and Henrich and Broesch’s15 2011 analysis of advice giving across small-scale populations in Fiji. Since the studies by Nolin7 and Henrich and Broesch15, ERGMs have featured in analyses of helping behaviour amongst the Hadza of Tanzania2, the Tamils of South India28,29,30, the Inuit of Canada31, the Tsimané33, and residents of small-scale populations on the Solomon Islands34. However, in these studies, ERGMs are only used to test for truncated degrees at zero (i.e., network isolates), self-reinforcing activity, simple reciprocity, and simple transitivity (i.e., the geometrically-weighted edgewise shared partners effect plus the geometrically-weighted dyadwise shared partners effect29 and, unusually, an effect for intransitivity34). Fisher et al.37 and Evans et al.36 review the history of SAOMs and ERGMs, respectively, across the broader behavioural ecology literature on animal social networks.
Note that there is no one-to-one correspondence between effects in SAOMs and effects in ERGMs. This is because the models use rather different dependence hierarchies — i.e., the set of assumptions around how ties feedback upon themselves. Furthermore, they reflect distinct assumptions about how social ties come into being — where ERGMs treat ties as “costless” and do not explicitly position tie formation as the result of individual decisions. That said, as implied in my comparison with SAOMs above, ERGMs are compatible with agency-based theories42,49.
Finally, recall that formulae for the statistics underpinning all SAOM effects used here, in addition to short descriptions to aid interpretation, appear in Online-Only Table 1. Ripley et al.44 also provide diagrams for effects that readers may find useful. Note that the interaction between Consanguineal Relatedness and Reciprocity is handled “internally” using the non-centred SAOM effect “XRecip” (Ripley et al.44, p. 140). However, the interaction between Consanguineal Relatedness and Relative Wealth Rank and the interaction between Consanguineal Relatedness and Geographic Distance are handled “externally” by multiplying the matrix for genetic relatedness with the matrix encoding the pairwise differences in wealth rank and the matrix encoding inter-household distance. These matrix products are then included in models using the non-centred SAOM effect “X” (Ripley et al.44, p. 140).
A note on “Reciprocity”
Recall that in a SAOM the formation of relationships and, by extension, the emergence of global network structure are rooted in the decisions of individual network members (hence, “actor-oriented”). Thus, for graphs composed of asymmetric relationships, network members can only control their outgoing ties. Accordingly, the Reciprocity effect concerns how receiving aid impacts one’s own propensity to give back (i.e., “reciprocal exchange” à la social exchange theory19 or “dyadic symmetry” à la structural balance theory48). As von Rueden et al.33 (p. 4) highlight, this is very different from the evolutionary strategy of “direct reciprocity” — i.e., helping someone and judging, with some probability, that the recipient of aid will return the favour in the future (see Allen-Arave et al.1 on reciprocal altruism and “contingent reciprocity”).
In this respect, the Reciprocity effect in and of itself only reveals whether there tends to be a direct payoff to asymmetric aid in the form of an in-kind response by those who have been helped — where, by design, SAOMs cannot tell us if this response is the immediate result of the evolutionary strategy of reciprocity. Nevertheless, to the extent that such a strategy is employed in a given population, SAOMs can hint at its usefulness. This is also the case for the Out-Degree Popularity effect and the evolutionary strategy of “indirect reciprocity” — i.e., helping others to increase one’s reputation as “cooperative” in order to benefit from the greater receipt of help from others in the future (see Smith et al.8, Simpson et al.20, and Melamed et al.88).
Network Diagram Construction
Figure 1 was created using Brandes and Wagner’s116 layout software Visone. Following Stadtfeld et al.115, the node layout was determined using Nocaj, Ortmann, and Brandes’117 network backbone algorithm which is designed to sparisfy graphs using a criterion based on the embeddedness of ties with the aim of increasing visual interpretability without degrading representation of meso- and macro-level network structure. The cut-off for the normalised weights used for the link sparsification behind node placement was set to 40%, where these weights are based on the embeddedness of ties in tetrads (see Nocaj et al.117 on the “quadrilateral Simmelian backbone”). The isolated node in the bottom left of the plot is for a villager who sends and receives zero ties in the source-recipient-verified tangible aid network. Note that no manual post-processing of any kind was performed when constructing the network diagram. That is, the network layout depicted in Fig. 1 was fully determined by the algorithm of Nocaj et al.117 as implemented in Visone116.
Ethics
This paper describes the secondary analysis of public data released by Koster27. No primary data collection was carried out for this research. The collection of the data re-analysed here was approved by the Institutional Review Board of the University of Cincinnati27. Koster’s27 data were collected with Informed Consent27.
Custom Code
Research for this paper was carried out using the open-source programming language R and widely-used R packages — all of which are detailed in the R script written for data transformation and data analysis.
Data availability
All data used for my analysis is available via GitHub: https://github.com/cohensimpson/smallnet_ScientificData. Permanent access to an archived version of these data is available via Zenodo118.
Code availability
All R code used for my analysis is available via GitHub: https://github.com/cohensimpson/smallnet_ScientificData. Permanent access to an archived version of this code is available via Zenodo118.
References
Allen-Arave, W., Gurven, M. & Hill, K. Reciprocal Altruism, Rather than Kin Selection, Maintains Nepotistic Food Transfers on an Ache Reservation. Evol. Hum. Behav. 29, 305–318 (2008).
Apicella, C. L., Marlowe, F. W., Fowler, J. H. & Christakis, N. A. Social Networks and Cooperation in Hunter-Gatherers. Nature 481, 497–501 (2012).
Hackman, J., Munira, S., Jasmin, K. & Hruschka, D. Revisiting Psychological Mechanisms in the Anthropology of Altruism. Hum. Nat. 28, 76–91 (2017).
Jaeggi, A. V. & Gurven, M. Reciprocity Explains Food Sharing in Humans and other Primates Independent of Kin Selection and Tolerated Scrounging: A Phylogenetic Meta-Analysis. Proc. R. Soc. B Biol. Sci. 280, 20131615 (2013).
Kasper, C. & Borgerhoff Mulder, M. Who Helps and Why?: Cooperative Networks in Mpimbwe. Curr. Anthropol. 56, 701–732 (2015).
Macfarlan, S. J., Quinlan, R. J. & Post, E. Emergent Matriliny in a Matrifocal, Patrilineal Population: A Male Coalitionary. Perspective. Philos. Trans. R. Soc. B Biol. Sci. 374, 20180073 (2019).
Nolin, D. A. Food-Sharing Networks in Lamalera, Indonesia: Reciprocity, Kinship, and Distance. Hum. Nat. 21, 243–268 (2010).
Smith, D. et al. A Friend in Need is a Friend Indeed: Need-Based Sharing, Rather Than Cooperative Assortment, Predicts Experimental Resource Transfers Among Agta Hunter-Gatherers. Evol. Hum. Behav. 40, 82–89 (2019).
Thomas, M. G. et al. Kinship Underlies Costly Cooperation in Mosuo Villages. R. Soc. Open Sci. 5, 171535 (2018).
Thomas, M. G., Næss, M. W., Bårdsen, B.-J. & Mace, R. Saami Reindeer Herders Cooperate with Social Group Members and Genetic Kin. Behav. Ecol. 26, 1495–1501 (2015).
Caudell, M., Rotolo, T. & Grima, M. Informal Lending Networks in Rural Ethiopia. Soc. Netw. 40, 34–42 (2015).
Lyle, H. F. & Smith, E. A. The Reputational and Social Network Benefits of Prosociality in an Andean Community. Proc. Natl. Acad. Sci. 111, 4820–4825 (2014).
Clech, L., Hazel, A. & Gibson, M. A. Does Kin-Selection Theory Help to Explain Support Networks among Farmers in South-Central Ethiopia? Hum. Nat. 30, 422–447 (2019).
Hooper, P. & DeDeo, S. Caldwell Hooper, A., Gurven, M. & Kaplan, H. Dynamical Structure of a Traditional Amazonian Social Network. Entropy 15, 4932–4955 (2013).
Henrich, J. & Broesch, J. On the Nature of Cultural Transmission Networks: Evidence from Fijian Villages for Adaptive Learning Biases. Philos. Trans. R. Soc. B Biol. Sci. 366, 1139–1148 (2011).
Page, A. E. et al. Testing Adaptive Hypotheses of Alloparenting in Agta Foragers. Nat. Hum. Behav. 3, 1154–1163 (2019).
Axelrod, R. & Hamilton, W. D. The Evolution of Cooperation. Science 211, 1390–1396 (1981).
Hedström, P. & Bearman, P. S. What is Analytical Sociology All About? An Introductory Essay. in The Oxford Handbook of Analytical Sociology (eds. Hedström, P. & Bearman, P. S.) 3–24 (Oxford University Press, 2009).
Molm, L. D. The Structure of Reciprocity. Soc. Psychol. Q. 73, 119–131 (2010).
Simpson, B., Harrell, A., Melamed, D., Heiserman, N. & Negraia, D. V. The Roots of Reciprocity: Gratitude and Reputation in Generalized Exchange Systems. Am. Sociol. Rev. 83, 88–110 (2018).
Wellman, B. Structural Analysis: From Method and Metaphor to Theory and Substance. in Social Structures: A Network Approach 19–61 (Cambridge University Press, 1988).
Zeggelink, E. Dynamics of Structure: An Individual Oriented Approach. Soc. Netw. 16, 295–333 (1994).
Su, Q., Li, A., Wang, L. & Eugene Stanley, H. Spatial Reciprocity in the Evolution of Cooperation. Proc. R. Soc. B Biol. Sci. 286, 20190041 (2019).
Rand, D. G., Arbesman, S. & Christakis, N. A. Dynamic Social Networks Promote Cooperation in Experiments with Humans. Proc. Natl. Acad. Sci. 108, 19193–19198 (2011).
Voelkl, B. & Kasper, C. Social Structure of Primate Interaction Networks Facilitates the Emergence of Cooperation. Biol. Lett. 5, 462–464 (2009).
Martí, J., Bolíbar, M. & Lozares, C. Network Cohesion and Social Support. Soc. Netw. 48, 192–201 (2017).
Koster, J. Family Ties: The Multilevel Effects of Households and Kinship on the Networks of Individuals. R. Soc. Open Sci. 5, 172159 (2018).
Power, E. A. & Ready, E. Cooperation Beyond Consanguinity: Post-Marital Residence, Delineations of Kin and Social Support among South Indian Tamils. Philos. Trans. R. Soc. B Biol. Sci. 374, 20180070 (2019).
Power, E. A. Collective Ritual and Social Support Networks in Rural South India. Proc. R. Soc. B Biol. Sci. 285, 20180023 (2018).
Power, E. A. Social Support Networks and Religiosity in Rural South India. Nat. Hum. Behav. 1, 0057 (2017).
Ready, E. & Power, E. A. Why Wage Earners Hunt: Food Sharing, Social Structure, and Influence in an Arctic Mixed Economy. Curr. Anthropol. 59, 74–97 (2018).
Redhead, D. & von Rueden, C. R. Coalitions and Conflict: A Longitudinal Analysis of Men’s Politics. Evol. Hum. Sci. 3, 1–20 (2021).
von Rueden, C. R., Redhead, D., O’Gorman, R., Kaplan, H. & Gurven, M. The Dynamics of Men’s Cooperation and Social Status in a Small-Scale Society. Proc. R. Soc. B Biol. Sci. 286, 20191367 (2019).
Bond, M. O. & Gaoue, O. G. Prestige and Homophily Predict Network Structure for Social Learning of Medicinal Plant Knowledge. PLOS ONE 15, e0239345 (2020).
Evans, J. C., Fisher, D. N. & Silk, M. J. The Performance of Permutations and Exponential Random Graph Models When Analyzing Animal Networks. Behav. Ecol. 31, 1266–1276 (2020).
Silk, M. J. & Fisher, D. N. Understanding Animal Social Structure: Exponential Random Graph Models in Animal Behaviour Research. Anim. Behav. 132, 137–146 (2017).
Fisher, D. N., Ilany, A., Silk, M. J. & Tregenza, T. Analysing Animal Social Network Dynamics: The Potential of Stochastic Actor-Oriented Models. J. Anim. Ecol. 86, 202–212 (2017).
Snijders, T. A. B. Statistical Models for Social Networks. Annu. Rev. Sociol. 37, 131–153 (2011).
Rivera, M. T., Soderstrom, S. B. & Uzzi, B. Dynamics of Dyads in Social Networks: Assortative, Relational, and Proximity Mechanisms. Annu. Rev. Sociol. 36, 91–115 (2010).
Snijders, T. A. B. & Steglich, C. E. G. Representing Micro–Macro Linkages by Actor-based Dynamic Network Models. Sociol. Methods Res. 44, 222–271 (2015).
Indlekofer, N. & Brandes, U. Relative Importance of Effects in Stochastic Actor-Oriented Models. Netw. Sci. 1, 278–304 (2013).
Block, P., Stadtfeld, C. & Snijders, T. A. B. Forms of Dependence: Comparing SAOMs and ERGMs From Basic Principles. Sociol. Methods Res. 48, 202–239 (2019).
Block, P. Reciprocity, Transitivity, and the Mysterious Three-Cycle. Soc. Netw. 40, 163–173 (2015).
Ripley, R. M., Snijders, T. A. B., Boda, Z., Vörös, A. & Preciado, P. Manual for RSiena (v. 1.3.6). (2022).
Simpson, C. R. Farm Size Shapes Friend Choice Amongst Rice Producers in China: Some Evidence for the Theory of Network Ecology. Soc. Netw. 61, 107–127 (2020).
Robins, G., Pattison, P. & Woolcock, J. Small and Other Worlds: Global Network Structures from Local Processes. Am. J. Sociol. 110, 894–936 (2005).
Stadtfeld, C., Takács, K. & Vörös, A. The Emergence and Stability of Groups in Social Networks. Soc. Netw. 60, 129–145 (2020).
Krackhardt, D. & Handcock, M. S. Heider vs Simmel: Emergent Features in Dynamic Structures. in Statistical Network Analysis: Models, Issues, and New Directions (eds. Airoldi, E. et al.) vol. 4503 14–27 (Springer Berlin Heidelberg, 2007).
Lusher, D., Koskinen, J. & Robbins, G. Exponential Random Graph Models for Social Networks: Theories, Methods, and Applications. (Cambridge University Press, 2013).
Nettle, D., Gibson, M. A., Lawson, D. W. & Sear, R. Human Behavioral Ecology: Current Research and Future Prospects. Behav. Ecol. 24, 1031–1040 (2013).
Pescosolido, B. A. The Sociology of Social Networks. in 21st Century Sociology(eds. Bryant, C. D. & Peck, D. L.) vol. 2, 208–217 (SAGE, 2007).
Snijders, T. A. B. Stochastic Actor-Oriented Models for Network Dynamics. Annu. Rev. Stat. Its Appl. 4, 343–363 (2017).
Block, P., Koskinen, J., Hollway, J., Steglich, C. & Stadtfeld, C. Change We Can Believe In: Comparing Longitudinal Network Models on Consistency, Interpretability and Predictive Power. Soc. Netw. 52, 180–191 (2018).
Snijders, T. A. B., Koskinen, J. & Schweinberger, M. Maximum Likelihood Estimation for Social Network Dynamics. Ann. Appl. Stat. 4, 567–588 (2010).
Snijders, T. A. B. The Statistical Evaluation of Social Network Dynamics. Sociol. Methodol. 31, 361–395 (2001).
Snijders, T. A. B. & Lomi, A. Beyond Homophily: Incorporating Actor Variables in Statistical Network Models. Netw. Sci. 7, 1–19 (2019).
Krause, R., Huisman, M. & Snijders, T. A. B. Multiple Imputation for Longitudinal Network Data. Ital. J. Appl. Stat. 30, 33–57 (2018).
Apicella, C. L. & Silk, J. B. The Evolution of Human Cooperation. Curr. Biol. 29, R447–R450 (2019).
Dyble, M., Gardner, A., Vinicius, L. & Migliano, A. B. Inclusive Fitness for In-Laws. Biol. Lett. 14, 20180515 (2018).
Doreian, P., Kapuscinski, R., Krackhardt, D. & Szczypula, J. A Brief History of Balance Through Time. J. Math. Sociol. 21, 113–131 (1996).
Goodreau, S. M., Kitts, J. A. & Morris, M. Birds of a Feather, or Friend of a Friend? Using Exponential Random Graph Models to Investigate Adolescent Social Networks. Demography 46, 103–125 (2009).
Feld, S. L. The Focused Organization of Social Ties. Am. J. Sociol. 86, 1015–1035 (1981).
Krackhardt, D. Simmelian Ties: Super Strong and Sticky. in Power and Influence in Organizations (eds. Kramer, R. M. & Neale, M. A.) 21–38 (SAGE Publications, Inc., 1998).
Lospinoso, J. & Snijders, T. A. B. Goodness of Fit for Stochastic Actor-Oriented Models. Methodol. Innov. 12, 205979911988428 (2019).
Schweinberger, M., Krivitsky, P. N., Butts, C. T. & Stewart, J. R. Exponential-Family Models of Random Graphs: Inference in Finite, Super and Infinite Population Scenarios. Stat. Sci. 35, 627–662 (2020).
Macfarlan, S. J., Quinlan, R. & Remiker, M. Cooperative Behaviour and Prosocial Reputation Dynamics in a Dominican Village. Proc. R. Soc. B Biol. Sci. 280, 20130557 (2013).
Snijders, T. A. B. Explained Variation in Dynamic Network Models. Mathématiques Sci. Hum. 168, 5–15 (2004).
Voorhees, B., Read, D. & Gabora, L. Identity, Kinship, and the Evolution of Cooperation. Curr. Anthropol. 61, 194–218 (2020).
Walker, R. S. et al. Living with Kin in Lowland Horticultural Societies. Curr. Anthropol. 54, 96–103 (2013).
Hamilton, M. J., Milne, B. T., Walker, R. S., Burger, O. & Brown, J. H. The Complex Structure of Hunter–Gatherer Social Networks. Proc. R. Soc. B Biol. Sci. 274, 2195–2203 (2007).
Wu, J.-J., Ji, T., He, Q.-Q., Du, J. & Mace, R. Cooperation is Related to Dispersal Patterns in Sino-Tibetan Populations. Nat. Commun. 6, 8693 (2015).
McFarland, D. A., Moody, J., Diehl, D., Smith, J. A. & Thomas, R. J. Network Ecology and Adolescent Social Structure. Am. Sociol. Rev. 79, 1088–1121 (2014).
Walker, R. S. Amazonian Horticulturalists Live in Larger, More Related Groups than Hunter–Gatherers. Evol. Hum. Behav. 35, 384–388 (2014).
Koster, J. et al. Kinship Ties Across the Lifespan in Human Communities. Philos. Trans. R. Soc. B Biol. Sci. 374, 20180069 (2019).
Smith, K. M. & Apicella, C. L. Partner Choice in Human Evolution: The role of Cooperation, Foraging Ability, and Culture in Hadza Campmate Preferences. Evol. Hum. Behav. 41, 354–366 (2020).
Gurven, M., Jaeggi, A. V., von Rueden, C., Hooper, P. L. & Kaplan, H. Does Market Integration Buffer Risk, Erode Traditional Sharing Practices and Increase Inequality? A Test among Bolivian Forager-Farmers. Hum. Ecol. 43, 515–530 (2015).
Colleran, H. Market Integration Reduces Kin Density in Women’s Ego-Networks in Rural Poland. Nat. Commun. 11, 266 (2020).
Glowacki, L. & Molleman, L. Subsistence Styles Shape Human Social Learning Strategies. Nat. Hum. Behav. 1, 0098 (2017).
Kammrath, L. K. et al. What Predicts Who We Approach for Social Support? Tests of the Attachment Figure and Strong Ties Hypotheses. J. Pers. Soc. Psychol. 118, 481–500 (2020).
Wellman, B. & Wortley, S. Different Strokes from Different Folks: Community Ties and Social Support. Am. J. Sociol. 96, 558–588 (1990).
Rijsewijk, L. G. M., Snijders, T. A. B., Dijkstra, J. K., Steglich, C. & Veenstra, R. The Interplay Between Adolescents’ Friendships and the Exchange of Help: A Longitudinal Multiplex Social Network Study. J. Res. Adolesc. 30, 63–77 (2020).
Small, M. L. & Sukhu, C. Because They Were There: Access, Deliberation, and the Mobilization of Networks for Support. Soc. Netw. 47, 73–84 (2016).
Kaplan, H. S., Hooper, P. L. & Gurven, M. The Evolutionary and Ecological Roots of Human Social Organization. Philos. Trans. R. Soc. B Biol. Sci. 364, 3289–3299 (2009).
Migliano, A. B. et al. Hunter-Gatherer Multilevel Sociality Accelerates Cumulative Cultural Evolution. Sci. Adv. 6, eaax5913 (2020).
Tokita, C. K. & Tarnita, C. E. Social Influence and Interaction Bias Can Drive Emergent Behavioural Specialization and Modular Social Networks Across Systems. J. R. Soc. Interface 17, 20190564 (2020).
Erikson, E. Formalist and Relationalist Theory in Social Network. Analysis. Sociol. Theory 31, 219–242 (2013).
Monge, P. R. & Contractor, N. Theories of Communication Networks. (Oxford University Press, 2003).
Melamed, D., Simpson, B. & Abernathy, J. The Robustness of Reciprocity: Experimental Evidence that Each Form of Reciprocity is Robust to the Presence of Other Forms of Reciprocity. Sci. Adv. 6, eaba0504 (2020).
Gelardi, V., Fagot, J., Barrat, A. & Claidière, N. Detecting Social (In)stability in Primates From Their Temporal Co-presence Network. Anim. Behav. 157, 239–254 (2019).
Ilany, A., Barocas, A., Koren, L., Kam, M. & Geffen, E. Structural Balance in the Social Networks of a Wild Mammal. Anim. Behav. 85, 1397–1405 (2013).
Wey, T. W., Jordán, F. & Blumstein, D. T. Transitivity and Structural Balance in Marmot Social Networks. Behav. Ecol. Sociobiol. 73, 88 (2019).
Ilany, A., Booms, A. S. & Holekamp, K. E. Topological Effects of Network Structure on Long-Term Social Network Dynamics in a Wild Mammal. Ecol. Lett. 18, 687–695 (2015).
Brent, L. J. N. Friends of Friends: Are Indirect Connections in Social Networks Important to Animal Behaviour? Anim. Behav. 103, 211–222 (2015).
Ilany, A., Holekamp, K. E. & Akçay, E. Rank-dependent Social Inheritance Determines Social Network Structure in Spotted Hyenas. Science 373, 348–352 (2021).
Ilany, A. & Akçay, E. Social Inheritance Can Explain the Structure of Animal Social Networks. Nat. Commun. 7, 12084 (2016).
Simpson, C. R. On the Structural Equivalence of Coresidents and the Measurement of Village Social. Structure. Soc. Netw. 69, 55–73 (2022).
Birkett, M. et al. Network Canvas: Key Decisions in the Design of an Interviewer-Assisted Network Data Collection Software Suite. Soc. Netw. 66, 114–124 (2021).
Stadtfeld, C., Snijders, T. A. B., Steglich, C. & van Duijn, M. Statistical Power in Longitudinal Network Studies. Sociol. Methods Res. 49, 1103–1132 (2020).
Gurven, M. To Give and to Give Not: The Behavioral Ecology of Human Food Transfers. Behav. Brain Sci. 27, 543–559 (2004).
Bliege Bird, R., Ready, E. & Power, E. A. The Social Significance of Subtle Signals. Nat. Hum. Behav. 2, 452–457 (2018).
Lee, F. & Butts, C. T. Mutual Assent or Unilateral Nomination? A Performance Comparison of Intersection and Union Rules for Integrating Self-Reports of Social Relationships. Soc. Netw. 55, 55–62 (2018).
Zachary, W. W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropol. Res. 33, 452–473 (1977).
Chuang, Y. & Schechter, L. Social Networks in Developing Countries. Annu. Rev. Resour. Econ. 7, 451–472 (2015).
Henrich, J., Heine, S. J. & Norenzayan, A. The Weirdest People in the World? Behav. Brain Sci. 33, 61–83 (2010).
Sah, P., Méndez, J. D. & Bansal, S. A Multi-species Repository of Social Networks. Sci. Data 6, 44 (2019).
Broido, A. D. & Clauset, A. Scale-Free Networks Are Rare. Nat. Commun. 10, 1017 (2019).
Breza, E., Chandrasekhar, A., Golub, B. & Parvathaneni, A. Networks in Economic Development. Oxf. Rev. Econ. Policy 35, 678–721 (2019).
Koster, J. M. Hunting and Subsistence among the Mayangna and Miskito of Nicaragua’s Bosawas Biosphere Reserve. (The Pennsylvania State University, 2007).
Koster, J. Interhousehold Meat Sharing among Mayangna and Miskito Horticulturalists in Nicaragua. Hum. Nat. 22, 394–415 (2011).
Koster, J. M. & Tankersley, K. B. Heterogeneity of Hunting Ability and Nutritional Status Among Domestic Dogs in Lowland Nicaragua. Proc. Natl. Acad. Sci. 109, E463–E470 (2012).
Koster, J. M., Grote, M. N. & Winterhalder, B. Effects on Household Labor of Temporary Out-migration by Male Household Heads in Nicaragua and Peru: an Analysis of Spot-check Time Allocation Data Using Mixed-effects Models. Hum. Ecol. 41, 221–237 (2013).
Ready, E. & Power, E. A. Measuring Reciprocity: Double Sampling, Concordance, and Network Construction. Netw. Sci. 9, 387–402 (2021).
Preciado, P., Snijders, T. A. B., Burk, W. J., Stattin, H. & Kerr, M. Does Proximity Matter? Distance Dependence of Adolescent Friendships. Soc. Netw. 34, 18–31 (2012).
Snijders, T. A. B., Faye, M. & Brailly, J. Network Dynamics with a Nested Node Set: Sociability in Seven Villages in Senegal. Stat. Neerlandica 74, 300–323 (2020).
Stadtfeld, C., Vörös, A., Elmer, T., Boda, Z. & Raabe, I. J. Integration in Emerging Social Networks Explains Academic Failure and Success. Proc. Natl. Acad. Sci. 116, 792–797 (2019).
Brandes, U. & Wagner, D. Analysis and Visualization of Social Networks. in Graph Drawing Software (eds. Jünger, M. & Mutzel, P.) 321–340 (Springer Berlin Heidelberg, 2004).
Nocaj, A., Ortmann, M. & Brandes, U. Untangling the Hairballs of Multi-Centered, Small-World Online Social Media Networks. J. Graph Algorithms Appl. 19, 595–618 (2015).
Simpson, C. R. github.com/cohensimpson/smallnet_ScientificData [Archived Repository of Replication Materials for ‘Social Support and Network Formation in a Small-Scale Horticulturalist Population’]. Zenodo https://doi.org/10.5281/ZENODO.6689517 (2022).
Acknowledgements
I thank Jeremy Koster for sharing his data, graciously fielding my queries, and kindly providing key feedback. Moreover, for their formative critique, I thank Per Block, Zachary H. Garfield, Luke Glowacki, David W. Lawson, and Felix C. Tropf as well as the two anonymous reviewers and Katherine Homewood, the handling editorial board member. For their research participation, I am also deeply grateful to the residents of Arang Dak. Finally, this work would not have been possible without the generous support of a British Academy Postdoctoral Fellowship (Grant Number: pf170158).
Author information
Authors and Affiliations
Contributions
C.R.S. designed the research, analysed the data, and wrote the report.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Online-only Table
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Simpson, C.R. Social Support and Network Formation in a Small-Scale Horticulturalist Population. Sci Data 9, 570 (2022). https://doi.org/10.1038/s41597-022-01516-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-022-01516-x