Abstract
While the GRACE (Gravity Recovery and Climate Experiment) satellite mission is of great significance in understanding various branches of Earth sciences, the quality of GRACE monthly products can be unsatisfactory due to strong longitudinal stripe-pattern errors and other flaws. Based on corrected GRACE Mascon (mass concentration) gridded mass transport time series and updated LDCgam (Least Difference Combination global angular momenta) data, we present a new set of monthly gravity models called LDCmgm90, in the form of Stokes coefficients with order and degree both up to 90. The LDCgam inputs are developed by assimilating degree-2 Stokes coefficients from various versions of GRACE (including Mascon products) and SLR (Satellite Laser Ranging) monthly gravity data into combinations of outputs from various global atmospheric, oceanic, and hydrological circulation models, under the constraints of accurately measured Earth orientation parameters in the Least Difference Combination (LDC) scheme. Taking advantages of the relative strengths of the various input solutions, the LDCmgm90 is free of stripes and some other flaws of classical GRACE products.
Measurement(s) | Stokes coefficient • Coefficient |
Technology Type(s) | spherical harmonic expansion • least difference combination • computational modeling technique |
Sample Characteristic - Environment | climate system |
Sample Characteristic - Location | Earth (planet) |
Machine-accessible metadata file describing the reported data: https://doi.org/10.6084/m9.figshare.9924929
Similar content being viewed by others
Background & Summary
Time-dependent gravity from the GRACE (Gravity Recovery and Climate Experiment) twin satellites is of great significance for studies related to changes in land water, ice sheets, sea level rise, ocean circulation, Earthquake dynamics etc.1,2,3,4,5,6,7. GRACE data are routinely provided almost every month (from Apr. 2002 to Jun. 2017, but with 20 months missing) in the form of Stokes coefficients with AOD1B (Atmosphere and Ocean Dealiasing Level 1B) corrections (denoted as GSM) by Center for Space Research (CSR), Deutsches GeoForschungsZentrum (GFZ), Jet Propulsion Laboratory (JPL) and Graz University of Technology (TUG), using a least squares adjustment (LSA) scheme8,9,10,11,12,13,14. There are often limited agreements between GRACE-based results and those obtained by independent observations, mostly attributed to the well-known strong striped noise patterns caused by the GRACE’s near-polar orbital inclination and the LSA scheme, which ignores the orthogonality of spherical harmonics and thus leads to correlations of Stokes coefficients15,16,17,18,19. Notable discrepancies can also be found among GRACE products released by different institutes, due to some differences in data processing strategies adopted by them8,9,10,11,12,13,19,20,21,22. Various filtering and destriping methods are proposed to attenuate these stripes, resulting in weaker and distorted signals of interest23,24,25,26,27,28. Moreover, power losses are also found around 3 cycles per year (cpy) and higher in time series of low degree GRACE Stokes coefficients21.
Since 2015, CSR and JPL also provide so-called Mascon solutions using the Mass Concentration blocks (mascons)29,30,31,32, another form of gravity field basis functions. With mascons, some a priori geophysical constraints can be implemented to remove noises from the GRACE observations at the Level-2 processing step, which is a much more rigorous approach than the empirical post-processing filtering and destriping of the LSA-based spherical harmonics. However, the problem of power losses around 3 cpy and higher is not overcome, and notable differences between CSR and JPL mascon solutions still exist (noted by this study).
Mass redistributions will cause changes not only in gravity but also in Earth’s pole coordinates and spin rate, due to conservation of angular momentum33,34. Plenty of studies have explored the links between the time-dependent Stokes coefficients and Earth rotational variations, specifically the level of agreement between GRACE-based (C21, S21) series and polar motion, and between SLR-based C20 and length-of-day (LOD) variations after contributions unrelated to mass redistributions are excluded21,35,36,37,38,39,40,41,42,43,44,45. Some even made use of these GRACE and/or SLR (Satellite Laser Ranging) coefficient series to improve geophysically based fluid model excitations of polar motion and LOD variations21,22,46. Among these studies, the Least Difference Combination (LDC) of global angular momenta for surficial geophysical fluids of Chen et al.21 and Yu et al.22 (hereafter termed as LDCgam) seem to have the best performances in both the frequency and time domains, since various versions (CSR, GFZ and JPL) of GRACE and SLR monthly gravity data (RL05) were assimilated into the outputs from various global atmospheric, oceanic, and hydrological circulation models, in the LDC scheme which can extract the best frequency components from various types of data sources provided that one or more proper reference data or models can be established21,47.
To summarize, the currently available GRACE monthly Stokes coefficients are unsatisfactory due to strong longitudinal stripe-pattern errors and other flaws while assimilating independent related observations may help to improve them. In this study, we used numerical integration to convert Mascon gridded mass to Stokes coefficients and applied necessary corrections as described in the next section. We also prepared for this study an updated LDCgam solution48 obtained by similar procedures in Chen et al.21 and Yu et al.22 but assimilating all RL05 and RL06 GRACE/SLR Stokes coefficients from CSR, GFZ, JPL and TUG, and all RL05 and RL06 Mascon gridded mass fields. Then we put forward the improved monthly gravity model set LDCmgm90, in the form of Stokes coefficients (complete from degree and order 2 to 90) since they are more convenient to use.
Methods
The GRACE monthly data are usually released together with the GRACE AOD1B products, which provide a model-based data-set (including GAA, GAB, GAC and GAD) that describes the time variations of the gravity potential at satellite altitudes that are caused by non-tidal mass variability in the atmosphere and oceans49,50,51. The GAA product describes the monthly non-tidal atmospheric mass anomalies simulated by the operational run of the atmosphere model ECMWF (European Centre for Medium-Range Weather Forecasts)52, GAB refers to monthly non-tidal oceanic mass anomalies simulated by the operational run of the (unconstrained) ocean model OMCT (Ocean Model for Circulation and Tides)53 (for RL05) or MPIOM (Max-Planck-Institute for Meteorology Ocean Model)54 (for RL06), GAC is the sum of GAA and GAB, and GAD can be regarded as a revised version of GAC with non-tidal atmospheric and oceanic mass anomalies only over ocean areas. GSM is just the gravity residual after GAA and GAB are removed from the GRACE observations (in other words, GSM + GAB + GAA is what GRACE satellites really measure). Consistent with this system, the LDCmgm90 data set also contains five subsets GAA, GAB, GAC, GAD and GSM, all with degree and order up to 90 because higher harmonics are not guaranteed by GRACE’s measurement resolution.
The general procedures to produce the LDCmgm90 are described in Fig. 1, which is explained next.
Flow chart describing the procedures to generate the monthly global gravity model series LDCmgm90. (a) General procedures. (b) Procedures to obtain and correct Stokes coefficients derived from different Mascon solutions. The weights are determined by Eq. (4) and lppt = long-period pole tide correction according to Wahr et al.20.
Step 1: Obtain the LDCmgm degree-2 zonal and tesseral potential coefficients
We first obtained elements of the inertia tensor (ΔIxz(t), ΔIyz(t), ΔIzz(t)) through the mass-redistribution-related (or mass-term) angular momenta LDCgam:
then the corresponding LDCmgm degree-2 zonal and tesseral potential coefficients31,52
In Eqs (1) and (2), Ω = 7.292115 10−5 rad/s is the mean spin rate of the Earth, k′ = −0.316 is the degree-2 load Love number33, M = 5.97236 × 1024 kg and a = 6378136.6 m are the mass and mean equatorial radius of the Earth55,56, respectively, ΔT is the change in the trace of the inertia tensor and equals zero in the current case that the global mass is conserved33,57.
The LDCgam provides atmospheric angular momentum (AAM), oceanic angular momentum (OAM) and hydrological angular momentum/cryospheric angular momentum (HAM/CAM), where the HAM/CAM is dominated by but not limited to changes in land water and ice, since all the non-atmospheric and non-oceanic mass redistributions are attributed to it. Therefore, we have the following links (→ means corresponding to):
Mass-term AAM → GAA C20, C21 and S21.
Mass-term OAM → GAB C20, C21 and S21.
Mass-term HAM/CAM → GSM C20, C21 and S21.
Then we can obtain the degree-2 GAA, GAB and GSM zonal and tesseral potential coefficients for the LDCmgm90 (please refer to the top half of Fig. 1a). Noting that CSR, GFZ, JPL and TUG all used the same AOD1B products for the given data releases (RL05 or RL06), and the JPL GAA, GAB, GAC and GAD products are the most complete, we thus chose the JPL RL06 GAA, GAB, GAC and GAD products to construct the LDCmgm90.
Step 2: Convert the Mascon gridded mass redistribution to corrected Stokes coefficients
Currently, there are three Mascon solutions CSR Mascon RL05, JPL Mascon RL05 and JPL Mascon RL06, of which the original Mascon gridded data correspond to the GSM products29,30,31. Although the RL05 and RL06 Mascon products are based on different static background geopotential model (which would cause biases among them), we are more interested in the time-dependent parts rather than the static ones when using GRACE-like products. With these biases removed, a proper combination can extract the best components from these three Mascon solutions since no original single solution is perfect as discussed in Background & Summary.
The Mascon data are represented in the form of equivalent water height Δh(θ, λ, t) on a 0.5 degree longitude-latitude grid but representing the equal-area geodesic grid of size 1 × 1 degree at the equator. The surface density for this thin layer is Δσ(θ, λ, t) = ρwΔh(θ, λ, t), where ρw = 1025 kg/m3 is the average density of sea water. Then the original Mascon gridded data may be converted to Stokes coefficients by58
where \(k{^{\prime} }_{n}\) is the degree-n load Love number (from Table 1 of Wahr et al.58), ρave = 5517 kg/m3 is the average density of the solid Earth.
The GAA RL05 produced by the ECMWF operational run contains the following two notable jumps49,59:
-
(1)
Between 2006-01-29 18 h and 2006-01-30 00 h
-
(2)
Between 2010-01-26 00 h and 2010-01-26 06 h
due to upgrades of the horizontal and vertical resolutions in the ECMWF model, which will lead to opposite jumps in all the corresponding RL05 versions of GSM and Mascon products. Moreover, the RL05 products adopted the non-linear IERS2010 mean pole correction56, which will cause a long-period pole tide in C21 and S21 and should be corrected as suggested by Wahr et al.20. For the two RL05 Mascon products, corrections of the jumps and long-period pole tide should be applied (see Fig. 1b) while the RL06 data are free of these flaws due to a homogeneous reanalysis of the ECMWF data and the adoption of a linear mean pole model. However, one must keep in mind that whichever RL05 or RL06, GAA and GAB are respectively derived from the ECMWF and OMCT (or MPIOM) operational outputs, which need further refinements as shown in detailed analyses by Chen et al.21,47 and Yu et al.22. Thus it would be better to replace them with the LDC-corrected GAA and GAB. Further, GAC = GAA + GAB, and GAD can also be obtained by applying an ocean mask to GAC.
By using Eq. (3) and applying the above-mentioned corrections and replacements, we can obtain the corrected Mascon Stokes coefficients as shown in Fig. 1b.
Step 3: Take weighted average of the corrected Mascon Stokes coefficients and obtain the final solutions
The GRACE-observed geopotential Vobs may be separated into two parts: the part \({V}_{obs}^{zt}\) including the degree-2 zonal and tesseral terms (namely the terms relevant with C20, C21 and S21), and the other \({V}_{obs}^{nzt}\) containing all other terms, namely \({V}_{obs}={V}_{obs}^{zt}+{V}_{obs}^{nzt}\). All the CSR, GFZ, JPL and TUG released GRACE data are from the same twin satellites, thus in principle, any overestimate or underestimate of \({V}_{obs}^{zt}\) will cause an opposite effect on \({V}_{obs}^{nzt}\). That is, \({V}_{obs}^{zt}\) and \({V}_{obs}^{nzt}\) must have the same errors for each given version of GRACE data. Based on this reasoning, the weights of the corrected Mascon Stokes coefficients may be estimated as
since C20, C21 and S21 obtained from LDCgam are the most accurate and may be approximately used as standards to infer errors in other data sets. In Eq. (4), std(x) means standard derivation of x. The corresponding relative weights of the three Mascon solutions can be found in Table 3b.
We can obtain the weighted average of the corrected Mascon Stokes coefficients except for C20, C21 and S21 as described in the bottom part of Fig. 1b.
Data Records
Availabilities of the data used in this study are summarized in Table 1. While most GRACE and SLR data sets are named after their releasing institutes, the latest GRACE data set computed at TUG is termed ITSG-Grace2018 (ITSG for short). Data after Aug. 2016 (7 data points in total) are not provided by all RL06 GRACE products, and are supplemented by the corresponding RL05 ones.
The LDCmgm90 dataset is provided in the netcdf 4.0 format and can be accessed via figshare60, which contains five subsets GAA, GAB, GAC, GAD and GSM, all in the form of Stokes coefficients complete from degree and order 2 to 90.
Technical Validation
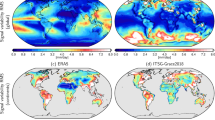
The degree-2 GSM zonal and tesseral Stokes coefficients from LDCmgm90 and other individual releases are compared in Fig. 2a, while the GSM + GAA + GAB ones are compared in Fig. 2b. One can see the coefficients from LDCmgm are less noisy and free of anomalous signals presented in some other GRACE products, since when combining or assimilating data from different sources, the LDC method can provide a good handle of both the magnitude and phase aspects simultaneously for arbitrary frequency including the lowest frequency component which is usually called the trend of a series21,47. The standard derivations of the original and corrected LDCmgm GSM (C20, C21, S21) with respect with those from other model sets are provided in Tables 2 and 3, respectively. In addition, Figs 1, 3, 4 and Table 4 of Chen et al.21 implied that our C21 and S21 (the corresponding geophysical excitations are denoted as LDCgsc) are the most consistent with the observed polar motion, while Fig. 9 and Table 5 of Yu et al.22 suggested our C20 agrees the best with the observed length-of-day variations. A further and more independent check of the LDCmgm90 would be to compute the loads from the monthly gravity fields and apply those to GPS time series. However, the complexity of such a check makes it impossible to include in this short data descriptor so that will left for later work.
The mutual differences of geopotential maps for two neighboring months are also compared in Fig. 3. One can see the one corresponding to LDCmgm90 has no stripes, thanks to the Mason solutions used, while those for CSR, GFZ, JPL and TUG (only the map for CSR RL06 is provided here) have strong stripe-pattern noises, which overwhelm any geophysical signal of interest.
Code availability
The MatLab codes used to generate the LDCmgm90 are available upon request to W. Chen (wchen@sgg.whu.edu.cn).
References
Tapley, B. D., Chambers, D. P., Bettadpur, S. & Ries, J. C. Large scale ocean circulation from the GRACE GGM01 Geoid. Geophys. Res. Lett. 30, 2163–2166 (2002).
Xing, W. et al. Estimating monthly evapotranspiration by assimilating remotely sensed water storage data into the extended Budyko framework across different climatic regions. J. Hydro. 567, 684–695 (2018).
Rahimi, A., Li, J., Naeeni, M. R., Shahrisvand, M. & Fatolazadeh, F. On the extraction of co-seismic signal for the Kuril Island earthquakes using GRACE observations. Geophy. J. Int. 215, 346–362 (2018).
Poropat, L. et al. Time variations in ocean bottom pressure from a few hours to many years: in situ data, numerical models, and GRACE satellite gravimetry. J. Geophys. Res. Oceans 123, 5612–5623 (2018).
Ran, J. J. et al. Seasonal mass variations show timing and magnitude of meltwater storage in the Greenland Ice Sheet. Cryosphere 12, 2981–2999 (2018).
Feng, W. & Zhong, M. Global sea level variations from altimetry, GRACE and Argo data over 2005–2014. Geod. Geodyn. 6, 274–279 (2015).
Chambers, D. P. Observing seasonal steric sea level variations with GRACE and satellite altimetry. J. Geophys. Res. 111, C03010 (2006).
Bettadpur, S. UTCSR level-2 processing standards document for level-2 product release 0005. Report No. GRACE 327–742 (Center for Space Research, 2012).
Bettadpur, S. UTCSR level-2 processing standards document for level-2 product release 0006. Report No. GRACE 327–742 (Center for Space Research, 2018).
Dahle, C. et al. GFZ GRACE level-2 processing standards document for level-2 product release 0005. Report No. STR12/02-data (Deutsches Geo Forschungs Zentrum, 2012).
Dahle, C. et al. GFZ level-2 processing standards document for level-2 product release 0006. Report No. STR18/04-data (Deutsches Geo Forschungs Zentrum, 2018).
Watkins, M. M. & Yuan, D. JPL level-2 processing standards document for level-2 product release 05.1. Report No. GRACE 327–744 (Jet Propulsion Laboratory, 2014).
Yuan, D. JPL level-2 processing standards document for level-2 product release 06. Report No. GRACE 327–744 (Jet Propulsion Laboratory, 2018).
Mayer-Gürr, T. et al. ITSG-Grace 2018-monthly, daily and static gravity field solutions from GRACE, https://doi.org/10.5880/ICGEM.2018.003 (2018).
Schrama, E. J. O., Wouters, B. & Lavallée, D. A. Signal and noise in gravity recovery and climate experiment (GRACE) observed surface mass variations. J. Geophys. Res. 112, B08407 (2007).
Swenson, S. & Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 33, L08402 (2006).
Wouters, B. & Schrama, E. J. O. Improved accuracy of GRACE gravity solutions through empirical orthogonal function filtering of spherical harmonics. Geophys. Res. Lett. 34, L23711 (2007).
Duan, X. J., Guo, J. Y., Shum, C. K. & van der Wal, W. On the postprocessing removal of correlated errors in GRACE temporal gravity field solutions. J. Geod. 83, 1095–1106 (2009).
Seo, K. W., Wilson, C. R., Han, S. C. & Waliser, D. E. Gravity Recovery and Climate Experiment (GRACE) alias error from ocean tides. J. Geophys. Res. 113, B03405 (2008).
Wahr, J., Nerem, R. S. & Bettadpur, S. V. The pole tide and its effect on GRACE time-variable gravity measurements: Implications for estimates of surface mass variations. J. Geophys. Res. Solid Earth 120, 4597–4615 (2015).
Chen, W., Li, J., Ray, J. & Cheng, M. Improved geophysical excitations constrained by polar motion observations and GRACE/SLR time-dependent gravity. Geod. Geodyn. 8, 377–388 (2017).
Yu, N., Li, J. C., Ray, J. & Chen, W. Improved geophysical excitation of length-of-day constrained by Earth orientation parameters and satellite gravimetry products. Geophys. J. Int. 214, 1633–1651 (2018).
Chen, J. L., Wilson, C. R. & Seo, K. W. Optimized smoothing of gravity recovery and climate experiment (GRACE) time-variable gravity observations. J. Geophys. Res. 111, B06408 (2006).
Davis, J. L., Tamisie, M. E., Elósegui, P., Mitrovica, J. X. & Hill, E. M. A statistical filtering approach for Gravity Recovery and Climate Experiment (GRACE) gravity data. J. Geophys. Res. 113, B04410 (2008).
Guo, J. Y., Duan, X. J. & Shum, C. K. Non-isotropic Gaussian smoothing and leakage reduction for determining mass changes over land and ocean using GRACE data. Geophys. J. Int. 181, 290–302 (2010).
Han, S. C. et al. Non-isotropic filtering of GRACE temporal gravity for geophysical signal enhancement. Geophys. J. Int. 163, 18–25 (2005).
Klees, R. et al. The design of an optimal filter for monthly GRACE gravity models. Geophys. J. Int. 175, 417–432 (2008).
Kusche, J. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. J. Geod. 81, 733–749 (2007).
Watkins, M. M., Wiese, D. N., Yuan, D.-N., Boening, C. & Landerer, F. W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 120, 2648–2671 (2015).
Wiese, D. N., Landerer, F. W. & Watkins, M. M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 52, 7490–7502 (2016).
Save, H., Bettadpur, S. & Tapley, B. D. High resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 121, 7547–7569 (2016).
Wiese, D. N., Yuan, D.-N., Boening, C., Landerer, F. W. & Watkins, M. M. JPL GRACE mascon ocean, ice, and hydrology equivalent water height release 06 coastal resolution improvement (CRI) filtered version 1.0, https://doi.org/10.5067/TEMSC-3MJC6 (2018).
Gross, R. S. Earth rotation variations – long period. In Treatise on Geophysics 2nd edn Vol. 3 (ed. Schubert, G.) Ch. 9 (Elsevier B. V., 2015).
Chen, W., Ray, J., Li, J. C., Huang, C. L. & Shen, W. B. Polar motion excitations for an Earth model with frequency-dependent responses: 1. A refined theory with insight into the Earth’s rheology and core-mantle coupling. J. Geophys. Res. Solid Earth 118, 4975–4994 (2013).
Nastula, J., Ponte, R. M. & Salstein, D. A. Comparison of polar motion excitation series derived from GRACE and from analyses of geophysical fluids. Geophys. Res. Lett. 34, L11306 (2007).
Chen, J. L. & Wilson, C. R. Low degree gravity changes from GRACE, Earth rotation, geophysical models, and satellite laser ranging. J. Geophys. Res. 113, B06402 (2008).
Fernández, L. Analysis of geophysical variations of the C20 coefficient of the geopotential. In International Association of Geodesy Symposia Vol. 133 (ed. Sideris, M.G.) (Springer, 2009)
Brzeziński, A., Nastula, J. & Kołaczek, B. Seasonal excitation of polar motion estimated from recent geophysical models and observations. J. Geodyn. 48, 235–240 (2009).
Seoane, L., Nastula, J., Bizouard, C. & Gambis, D. The use of gravimetric data from GRACE mission in the understanding of polar motion variations. Geophys. J. Int. 178, 614–622 (2009).
Jin, S., Chambers, D. P. & Tapley, B. D. Hydrological and oceanic effects on polar motion from GRACE and models. J. Geophys. Res. 115, B02403 (2010).
Jin, S., Zhang, L. J. & Tapley, B. D. The understanding of length-of-day variations from satellite gravity and laser ranging measurements. Geophys. J. Int. 184, 651–660 (2011).
Seoane, L., Biancale, R. & Gambis, D. Agreement between Earth’s rotation and mass displacement as detected by GRACE. J. Geodyn. 62, 49–55 (2012).
Yan, H. & Chao, B. F. Effect of global mass conservation among geophysical fluids on the seasonal length of day variation. J. Geophys. Res. 117, B02401 (2012).
Meyrath, T. & van Dam, T. A comparison of interannual hydrological polar motion excitation from GRACE and geodetic observations. J. Geod. 99, 1–9 (2016).
Göttl, F., Schmidt, M. & Seitz, F. Mass-related excitation of polar motion: an assessment of the new RL06 GRACE gravity field models. Earth, Planets and Space 70, 195 (2018).
Göttl, F., Schmidt, M., Seitz, F. & Bloßfeld, M. Separation of atmospheric, oceanic and hydrological polar motion excitation mechanisms based on a combination of geometric and gravimetric space observations. J. Geod. 89, 377–390 (2015).
Chen, W., Ray, J., Shen, W. & Huang, C. Polar motion excitations for an Earth model with frequency-dependent responses: 2. Numerical tests of the meteorological excitations. J. Geophys. Res.: Solid Earth 118, 4995–5007 (2013).
Chen, W., Luo, J., Ray, J., Yu, N. & Li, J. C. LDCgam global angular momenta for surficial geophysical fluids, https://doi.org/10.13140/RG.2.2.28698.49604 (2019)
Flechtner, F., Dobslaw, H. & Fagiolini, E. Gravity Recovery and Climate Experiment: AOD1B product description document for product release 05, Report No. GRACE327-750 (Deutsches GeoForschungsZentrum, 2014).
Dobslaw, H. et al. Simulating high-frequency atmosphere-ocean mass variability for dealiasing of satellite gravity observations: AOD1B RL05. J. Geophys. Res. Oceans 118, 3704–3711 (2013).
Dobslaw, H. et al. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 211, 263–269 (2017).
Persson, A. & Grazzini, F. User guide to ECMWF forecast products, Report No. Meteorological Bulletin M3.2. (Deutsches GeoForschungsZentrum, 2007).
Thomas, M. Ocean induced variations of Earth’s rotation – Results from a simultaneous model of global circulation and tides, PhD thesis, 129 pp., Univ. of Hamburg, Hamburg, Germany (2002).
Jungclaus, J. H. et al. Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM) the ocean component of the MPI-Earth system model. J. Adv. Model Earth Syst. 5(2), 422–446 (2013).
Chen, W., Li, J. C., Ray, J., Shen, W. & Huang, C. L. Consistent estimates of the dynamical figure parameters of the Earth. J. Geod. 89, 179–188 (2015).
Petit, G. & Luzum, B. (eds) IERS conventions (2010), IERS Technical Notes 36, Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 179 pp., ISBN 3-89888-989-6 (2010).
Rochester, M. G. & Smylie, D. E. On changes in the trace of the Earth’s inertia tensor. J. Geophys. Res. 79, 4948–4951 (1974).
Wahr, J., Molenaar, M. & Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 103, 30205–30229 (1998).
Fagiolini, E., Flechtner, F., Horwath, M. & Dobslaw, H. Correction of inconsistencies in ECMWF’s operational analysis data during de-aliasing of GRACE gravity models. Geophys. J. Int. 202, 2150–2158 (2015).
Chen, W., Luo, J., Ray, J., Yu, N. & Li, J. C. LDCmgm90 monthly geopotential model set. figshare. https://doi.org/10.6084/m9.figshare.7874384.v1 (2019).
CSR GRACE level-2 RL05 solutions, ftp://isdcftp.gfz-potsdam.de/grace/ (2018).
CSR GRACE level-2 RL06 solutions, ftp://isdcftp.gfz-potsdam.de/grace/ (2019).
Cheng, M. & Tapley, B. D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. 109, B09402 (2004).
Cheng, M., Ries, J. C. & Tapley, B. D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. 116, B01409 (2011).
Cheng, M., Tapley, B. D. & Ries, J. C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 118, 740–747 (2013).
GFZ GRACE level-2 RL05 solutions, ftp://isdcftp.gfz-potsdam.de/grace/ (2018).
GFZ GRACE level-2 RL06 solutions, ftp://isdcftp.gfz-potsdam.de/grace/ (2019).
JPL GRACE level-2 RL05 solutions, ftp://isdcftp.gfz-potsdam.de/grace/ (2018).
JPL GRACE level-2 RL06 solutions, ftp://isdcftp.gfz-potsdam.de/grace/ (2019).
Acknowledgements
The editorial board member Dr. Kurt Kjær and two reviewers are highly appreciated for their insightful comments and suggestions, which helped to improve this study. We also thank the CSR, GFZ, JPL and TUG GRACE/SLR teams for making the GRACE/SLR monthly solutions publicly available. The CSR GRACE mascon solutions were downloaded from http://www2.csr.utexas.edu/grace, while the JPL mascon data are available at http://grace.jpl.nasa.gov, supported by the NASA MEaSUREs Program. This study is supported in parts by the National Natural Science Foundation of China (Nos 41874025 and 41474022), and the Fundamental Research Funds for the Central Universities of China (No. 2042016kf0146).
Author information
Authors and Affiliations
Contributions
W. Chen designed the framework of this study and performed part of the numerical computations. J. Luo and N. Yu processed the data and also contributed to numerical computations. J. Ray and J. Li helped to refine the research framework.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
The Creative Commons Public Domain Dedication waiver http://creativecommons.org/publicdomain/zero/1.0/ applies to the metadata files associated with this article.
About this article
Cite this article
Chen, W., Luo, J., Ray, J. et al. Multiple-data-based monthly geopotential model set LDCmgm90. Sci Data 6, 228 (2019). https://doi.org/10.1038/s41597-019-0239-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-019-0239-7
This article is cited by
-
Estimating GRACE terrestrial water storage anomaly using an improved point mass solution
Scientific Data (2023)
-
Free decay and excitation of the chandler wobble: self-consistent estimates of the period and quality factor
Journal of Geodesy (2023)
-
The influence of Antarctic ice loss on polar motion: an assessment based on GRACE and multi-mission satellite altimetry
Earth, Planets and Space (2021)