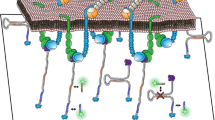
Abstract
Despite the vital role of mechanical forces in biology, it still remains a challenge to image cellular force with sub-100-nm resolution. Here, we present tension points accumulation for imaging in nanoscale topography (tPAINT), integrating molecular tension probes with the DNA points accumulation for imaging in nanoscale topography (DNA-PAINT) technique to map piconewton mechanical events with ~25-nm resolution. To perform live-cell dynamic tension imaging, we engineered reversible probes with a cryptic docking site revealed only when the probe experiences forces exceeding a defined mechanical threshold (~7–21 pN). Additionally, we report a second type of irreversible tPAINT probe that exposes its cryptic docking site permanently and thus integrates force history over time, offering improved spatial resolution in exchange for temporal dynamics. We applied both types of tPAINT probes to map integrin receptor forces in live human platelets and mouse embryonic fibroblasts. Importantly, tPAINT revealed a link between platelet forces at the leading edge of cells and the dynamic actin-rich ring nucleated by the Arp2/3 complex.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Data supporting the main figures in this work are available at https://doi.org/10.15139/S3/WB168Q. Other data that support the findings of this study are available from the corresponding authors upon reasonable request. Further information regarding the experimental design may be found in the Nature Research Reporting Summary.
Code availability
Filtering algorithms are derived from published methods31. The code is available from the corresponding author upon reasonable request.
References
Discher, D. E., Janmey, P. & Wang, Y. L. Tissue cells feel and respond to the stiffness of their substrate. Science 310, 1139–1143 (2005).
Qiu, Y. et al. Platelet mechanosensing of substrate stiffness during clot formation mediates adhesion, spreading, and activation. Proc. Natl Acad. Sci. USA 111, 14430–14435 (2014).
Liu, Y. et al. DNA-based nanoparticle tension sensors reveal that T-cell receptors transmit defined pN forces to their antigens for enhanced fidelity. Proc. Natl Acad. Sci. USA 113, 5610–5615 (2016).
Brockman, J. M. & Salaita, K. Mechanical proofreading: a general mechanism to enhance the fidelity of information transfer between cells. Front. Phys. 7, 14 (2019).
Kanchanawong, P. et al. Nanoscale architecture of integrin-based cell adhesions. Nature 468, 580–584 (2010).
Spiess, M. et al. Active and inactive β1 integrins segregate into distinct nanoclusters in focal adhesions. J. Cell Biol. 217, 1929–1940 (2018).
Stabley, D. R., Jurchenko, C., Marshall, S. S. & Salaita, K. S. Visualizing mechanical tension across membrane receptors with a fluorescent sensor. Nat. Methods 9, 64–67 (2012).
Liu, Y., Yehl, K., Narui, Y. & Salaita, K. Tension sensing nanoparticles for mechano-imaging at the living/nonliving interface. J. Am. Chem. Soc. 135, 5320–5323 (2013).
Galior, K., Liu, Y., Yehl, K., Vivek, S. & Salaita, K. Titin-based nanoparticle tension sensors map high-magnitude integrin forces within focal adhesions. Nano Lett. 16, 341–348 (2016).
Grashoff, C. et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature 466, 263–266 (2010).
Zhang, Y., Ge, C., Zhu, C. & Salaita, K. DNA-based digital tension probes reveal integrin forces during early cell adhesion. Nat. Commun. 5, 5167 (2014).
Blakely, B. L. et al. A DNA-based molecular probe for optically reporting cellular traction forces. Nat. Methods 11, 1229 (2014).
Blanchard, A. T. & Salaita, K. Emerging uses of DNA mechanical devices. Science 365, 1080–1081 (2019).
Ma, V. P.-Y. & Salaita, K. DNA nanotechnology as an emerging tool to study mechanotransduction in living systems. Small 15, 1900961 (2019).
Sahl, S. J., Hell, S. W. & Jakobs, S. Fluorescence nanoscopy in cell biology. Nat. Rev. Mol. Cell Biol. 18, 685–701 (2017).
Dai, M., Jungmann, R. & Yin, P. Optical imaging of individual biomolecules in densely packed clusters. Nat. Nanotechnol. 11, 798–807 (2016).
Schnitzbauer, J., Strauss, M. T., Schlichthaerle, T., Schueder, F. & Jungmann, R. Super-resolution microscopy with DNA-PAINT. Nat. Protoc. 12, 1198–1228 (2017).
Jungmann, R. et al. Multiplexed 3D cellular super-resolution imaging with DNA-PAINT and Exchange-PAINT. Nat. Methods 11, 313–318 (2014).
Jayasinghe, I. et al. True molecular scale visualization of variable clustering properties of ryanodine receptors. Cell Rep. 22, 557–567 (2018).
Whitley, K. D., Comstock, M. J. & Chemla, Y. R. Elasticity of the transition state for oligonucleotide hybridization. Nucleic Acids Res. 45, 547–555 (2017).
Woodside, M. T. et al. Nanomechanical measurements of the sequence-dependent folding landscapes of single nucleic acid hairpins. Proc. Natl Acad. Sci. USA 103, 6190–6195 (2006).
Brockman, J. M. et al. Mapping the 3D orientation of piconewton integrin traction forces. Nat. Methods 15, 115–118 (2018).
Zhang, Y. et al. Platelet integrins exhibit anisotropic mechanosensing and harness piconewton forces to mediate platelet aggregation. Proc. Natl Acad. Sci. USA 115, 325–330 (2018).
Ting, L. H. et al. Contractile forces in platelet aggregates under microfluidic shear gradients reflect platelet inhibition and bleeding risk. Nat. Commun. 10, 1204 (2019).
Chen, Y. et al. An integrin ɑIIbβ3 intermediate affinity state mediates biomechanical platelet aggregation. Nat. Mater. 18, 760–769 (2019).
Kong, F., Garcia, A. J., Mould, A. P., Humphries, M. J. & Zhu, C. Demonstration of catch bonds between an integrin and its ligand. J. Cell Biol. 185, 1275–1284 (2009).
Schueder, F. et al. An order of magnitude faster DNA-PAINT imaging by optimized sequence design and buffer conditions. Nat. Methods 16, 1101–1104 (2019).
Liu, Y. et al. Nanoparticle tension probes patterned at the nanoscale: impact of integrin clustering on force transmission. Nano Lett. 14, 5539–5546 (2014).
Plotnikov, S. V., Pasapera, A. M., Sabass, B. & Waterman, C. M. Force fluctuations within focal adhesions mediate ECM-rigidity sensing to guide directed cell migration. Cell 151, 1513–1527 (2012).
Gustafsson, N. et al. Fast live-cell conventional fluorophore nanoscopy with ImageJ through super-resolution radial fluctuations. Nat. Commun. 7, 12471 (2016).
Levet, F. et al. SR-Tesseler: a method to segment and quantify localization-based super-resolution microscopy data. Nat. Methods 12, 1065–1071 (2015).
Mayr, S. et al. Localization microscopy of actin cytoskeleton in human platelets. Int. J. Mol. Sci. 19, 1150 (2018).
Bearer, E. L., Prakash, J. M. & Li, Z. Actin dynamics in platelets. Int. Rev. Cytol. 217, 137–182 (2002).
Hartwig, J. H. Mechanisms of actin rearrangements mediating platelet activation. J. Cell Biol. 118, 1421–1442 (1992).
Gaertner, F. et al. Migrating platelets are mechano-scavengers that collect and bundle bacteria. Cell 171, e1323 (2017).
Li, Z., Kim, E. S. & Bearer, E. L. Arp2/3 complex is required for actin polymerization during platelet shape change. Blood 99, 4466–4474 (2002).
Wang, X. & Ha, T. Defining single molecular forces required to activate integrin and notch signaling. Science 340, 991–994 (2013).
Endesfelder, U., Malkusch, S., Fricke, F. & Heilemann, M. A simple method to estimate the average localization precision of a single-molecule localization microscopy experiment. Histochem. Cell Biol. 141, 629–638 (2014).
Strauss, S. et al. Modified aptamers enable quantitative sub-10-nm cellular DNA-PAINT imaging. Nat. Methods 15, 685–688 (2018).
Li, J. et al. Exploring the speed limit of toehold exchange with a cartwheeling DNA acrobat. Nat. Nanotechnol. 13, 723–729 (2018).
Polacheck, W. J. & Chen, C. S. Measuring cell-generated forces: a guide to the available tools. Nat. Methods 13, 415–423 (2016).
Colin-York, H. et al. Super-resolved traction force microscopy (STFM). Nano Lett. 16, 2633–2638 (2016).
Cox, S. et al. Bayesian localization microscopy reveals nanoscale podosome dynamics. Nat. Methods 9, 195–200 (2011).
Morimatsu, M., Mekhdjian, A. H., Chang, A. C., Tan, S. J. & Dunn, A. R. Visualizing the interior architecture of focal adhesions with high-resolution traction maps. Nano Lett. 15, 2220–2228 (2015).
Pryshchep, S., Zarnitsyna, V. I., Hong, J., Evavold, B. D. & Zhu, C. Accumulation of serial forces on TCR and CD8 frequently applied by agonist antigenic peptides embedded in MHC molecules triggers calcium in T cells. J. Immunol. 193, 68–76 (2014).
Elosegui-Artola, A. et al. Mechanical regulation of a molecular clutch defines force transmission and transduction in response to matrix rigidity. Nat. Cell Biol. 18, 540–548 (2016).
Blanchard, A. T., Brockman, J. M., Salaita, K. & Mattheyses, A. L. Variable incidence angle linear dichroism (VALiD): a technique for unique 3D orientation measurement of fluorescent ensembles. Opt. Express 28, 10039–10061 (2020).
Pan, H., Xia, Y., Qin, M., Cao, Y. & Wang, W. A simple procedure to improve the surface passivation for single molecule fluorescence studies. Phys. Biol. 12, 045006 (2015).
Hua, B. et al. An improved surface passivation method for single-molecule studies. Nat. Methods 11, 1233–1236 (2014).
Bazrafshan, A. et al. Tunable DNA origami motors translocate ballistically over μm distances at nm/s speeds. Angew. Chemie Int. Ed. Engl. 59, 9514–9521 (2020).
Douglas, S. M., Chou, J. J. & Shih, W. M. DNA-nanotube-induced alignment of membrane proteins for NMR structure determination. Proc. Natl Acad. Sci. USA 104, 6644–6648 (2007).
Galush, W. J., Nye, J. A. & Groves, J. T. Quantitative fluorescence microscopy using supported lipid bilayer standards. Biophys. J. 95, 2512–2519 (2008).
Vacklin, H. P., Tiberg, F. & Thomas, R. K. Formation of supported phospholipid bilayers via co-adsorption with β-d-dodecyl maltoside. Biochim. Biophys. Acta 1668, 17–24 (2005).
Acknowledgements
J.M.B., A.T.B. and R.G. acknowledge NSF GRFP grant no. 1444932. J.M.B. acknowledges NCI fellowship grant no. F99CA234959. A.T.B. acknowledges NCI fellowship grant no. F99CA245789. A.V.K. acknowledges NIH grant no. F31 F31CA243502. M.E.Q. acknowledges NIH grant no. F31 F31HL134241. H.O. acknowledges a grant from The Naito Foundation and a postdoctoral fellowship from The Uehara Memorial Foundation. B.G.P. acknowledges NIH grant no. HL117061. R.L. acknowledges NIH grant no. HL082808. Y.K. acknowledges NIH grant no. 1R21AI135753–01. A.L.M. acknowledges NSF CAREER grant no. 1832100. A.L.M. and K.S. acknowledge NIH grant no. R01GM131099. K.S. acknowledges NIH grant no. R01GM124472. We thank V.P.-Y. Ma for helpful discussions.
Author information
Authors and Affiliations
Contributions
J.M.B., H.S., Y.K. and K.S. designed the study. J.M.B., H.S., A.B., A.V.K., R.L.B., H.O. and R.G. performed experiments. J.M.B. and H.S. analyzed data. Y.D. and T.M. designed and synthesized DNA origami. E.M.Q., B.G.P. and R.L. assisted with platelet experiments. A.T.B. performed computational modeling. R.M. assisted with probe design. F.S. and R.J. assisted with design and optimization of speed-optimized tPAINT probes. A.L.M., Y.K. and K.S. supervised the study. J.M.B., H.S. and K.S. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Rita Strack was the primary editor on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Strain-free (sf)-tPAINT probe modeling and testing shows significant advantages over conventional hairpin probes (strained-tPAINT probes).
a, Schematic of binding of imagers to strain-free (sf-tPAINT) and conventional/strained probes. b, Total energy and change in energy as a function of applied force as predicted by the kinetic model described in Supplementary Note 2. c, Docking site occupancy as a function of applied F for strained (red), and sf-tPAINT probes (green) at 10 nM imager and (d) for varying imager concentration. Force impedes imager binding to strained but not sf-tPAINT probes. e–h, Experimental validation that sf-tPAINT probes outperform strained probes. e, Strain-free and f, conventional (strained) probes tagged with Cy3B-BHQ2 report pN tension as fluorescence. Images representative of n = 6 (e) and n = 3 experiments (f). g, Strain-free and h, conventional/strained probes were incubated with 10 nM Cy3B-imager and imaged in TIRF excitation. These images were reconstructed from 5000 frames of single molecule localizations. Data shown in g, h are from paired experiments using different fluidic channels on the same glass coverslip and using the same platelet donor. The results shown are representative of n = 3 experiments. i–k, Quantification of single molecule localizations (μm-2 s-1) for strained and sf-tPAINT probes. Results are representative of n = 4 (11 images) independent experiments for strained tPAINT surfaces and n = 6 independent sf-tPAINT surfaces (8 images). Data in k is displayed as mean with 95% CI. Cell (strained tPAINT): Mean= 0.29, 95% CI 0.12–0.46; Background (strained tPAINT): Mean= 0.06, 95% CI 0.04–0.07; Cell (sf-tPAINT): Mean= 1.09, 95% CI 0.89–1.29; Background (sf-tPAINT): Mean= 0.22, 95% CI 0.16–0.27. To determine the statistical significance, student t-test was applied to the data and the exact p-values are calculated (2 tailed, 2 sample). Cell (strained tPAINT) vs Background (strained tPAINT): 1.5×10–2, Cell (sf-tPAINT) vs Background (sf-tPAINT): 7.2×10−7, Cell (strained tPAINT) vs Cell (sf-tPAINT): 2.3×10−6, Background (strained tPAINT) vs Background (sf-tPAINT): 8.4×10−5.
Extended Data Fig. 2 Collage of examples showing accumulated-tPAINT and ~8.5 pN sf-tPAINT integrin tension maps for MEFs and human platelets.
Representative examples of images for MEF GFP-vinculin cells and human platelets displayed with a 5x density filter and kinetic filter. Images are representative of: 12pN Ttol accumulated-tPAINT maps, platelets, n = 8 replicates (22 images), and fibroblasts, n = 9 replicates (24 images); 7.3pN sf-tPAINT maps, fibroblasts, n = 3 experiments (cell culture media, 0.8 mM Mg2+), 8.5pN sf-tPAINT platelet maps, n = 4 experiments (Tyrode’s buffer + 2 mM Mg2+); sf-tPAINT maps in media supplemented with Mg2+, n = 3 independent platelet experiments (37.5 mM Mg2+) from 3 different donors (8 images) and n = 4 fibroblast experiments (75 mM Mg2+ 10 images).
Extended Data Fig. 3 Mechanoselection produces a signal-to-background ratio of up to 10 for sf-tPAINT probes and 17 for accumulated-tPAINT probes.
Human platelets were seeded on surfaces presenting cRGD-modified (a) 12pN Ttol accumulated-tPAINT probes at low [Mg2+], (b) sf-tPAINT probes at low [Mg2+], and (c) sf-tPAINT probes with 37.5 mM Mg2+. Note that the images displayed are raw-unfiltered single molecule localizations of tPAINT images with the contrast adjusted to emphasize the background localizations. d, The average per image localizations (µm−2s−1) for both the background and for the mechanical “footprint” of platelets (3 ROIs per image) is plotted. Results were obtained from n = 4 independent accumulated-tPAINT surfaces, n = 8 sf-tPAINT surfaces and n = 3 high [Mg2+] sf-tPAINT surfaces (10 images for accumulated-tPAINT, 16 images for strain-free, 7 images for high [Mg2+] strain-free). Mean ± standard deviation is noted above each category, error bar is mean with 95% CI. Cell (accumulated-tPAINT): Mean= 1.37, 95% CI 0.89–1.84; Background (accumulated-tPAINT): Mean= 0.08, 95% CI 0.02–0.04; Cell (strain-free tPAINT): Mean= 0.94, 95% CI 0.76–1.13; Background (sf-tPAINT): Mean= 0.17, 95% CI 0.12–0.22. Cell (high [Mg2+] sf-tPAINT): Mean= 3.88, 95% CI 3.00–4.76; Background (high [Mg2+] sf-tPAINT): Mean= 0.39, 95% CI 0.32–0.45. Student’s t-test was (2-tailed, 2 sample) was applied to determine significance. Cell (accumulated-tPAINT) vs Background (accumulated-tPAINT): p = 1.6×10−4, Cell (strain-free) vs Background (strain-free): p = 1.3×10−7, Cell (High [Mg2+] strain-free) vs Background (High [Mg2+] strain-free): p = 6.5×10−5, Cell (accumulated-tPAINT) vs Cell (strain-free): p = 8.5×10−2, Cell (accumulated-tPAINT) vs Cell (High [Mg2+] strain-free): p = 1.3×10−4, Cell (strain-free) vs Cell (High [Mg2+] strain-free): p = 1.2×10−4, Background (accumulated-tPAINT) vs Background (strain-free): p = 8.4×10−5. Background (accumulated-tPAINT) vs Background (strain-free): p = 5.2×10−3, Background (accumulated-tPAINT) vs Background (High [Mg2+] strain-free): p = 1.1×10−6, Background (strain-free) vs Background (High [Mg2+] strain-free): p = 1.7×10−5.
Extended Data Fig. 4 Analysis of lamellipodial and focal adhesion dynamics using time resolved 8.5pN sf-tPAINT.
a, 8.5 pN tPAINT integrin forces (red points) and RICM (grey scale image) were simultaneously imaged in a spreading human platelet. Each RICM image was collected at the beginning of the time window, while the 8.5pN sf-tPAINT data represents the accumulated signal in a 60 sec interval. b, Zoom-in images of the region highlighted with yellow box in (a). The green arrow denotes the formation of a filopodium and the force associated with extension of this structure. For frames corresponding to minutes 1–10, the cell edge in the previous frame is highlighted with a dashed yellow line. Note that the filopodial forces are still resolved even after lamellipodial spreading. c, Full cell view of a mouse embryonic fibroblast (MEF); d, e, show zoom-ins of the regions highlighted with yellow and blue boxes, respectively. Note that the focal adhesion (as indicated by the vinculin-GFP data) is offset from the mechanical localizations. The tension signal extends beyond the tip of the focal adhesions away from the cell body, and this is clear both in the full view of the cell (c), as well as the zoom in panels (d) and (e). This could be consistent with previous reports by Waterman and colleagues which found that the centroid of focal adhesion traction stresses is consistently ~1μm distal to the focal adhesion centroid29. This finding is also consistent with previous publications from our lab28, and the diffraction limited tension reported in Supplementary Fig. 3 of this work. Data shown is representative of: platelets, n = 3 independent experiments (5 images); fibroblasts, n = 3 independent experiments (5 images).
Extended Data Fig. 5 Design of speed-optimized strain-free tPAINT probes.
a, Schematic of sf-tPAINT probes. b, NUPACK modeling of self-base-pairing propensity of the imager. c, Sequences/designs of speed-optimized sf-tPAINT docking sites (blue strand) that avoid self-interaction. Imager docking site highlighted in pink. d, Representative speed sf-tPAINT images of MEF GFP-vinculin cells imaged in cell culture media (~0.8 mM Mg2+) and in 75 mM Mg2+ supplemented media. e, NUPACK modeling of speed sf-tPAINT probes. f, Ratio of tPAINT localizations versus background localizations. Each point in (f) is a single cell. Number of replicates: v1_no Mg2+ (5 cells, n = 3 experiments), v1_ Mg2+ (3 cells, n = 3 experiments), v2_no Mg2+(6 cells, n = 3 experiments), v2_Mg2+ (3 cells, n = 3 experiments), v3_no Mg2+ (8 cells, n = 3 experiments), v3_Mg2+(5 cells, n = 3 experiments), and v3_spacer_no Mg2+(16 cells, n = 4 experiments), v3_spacer_Mg2+ (8 cells, n = 4 experiments), v3_control_no Mg2+ (4 cells, n = 4 experiments), v3_control_Mg2+ (7 cells, n = 3 experiments). All scale bars are 5 μm. Data were compared via a 2-way ANOVA. v3_spacer (in the no added Mg2+ case) is statistically different from v1 (p = 5.3×10−10), v2 (p = 6.4×10−8), v3 (p = 0.0022), and v3_control (p = 2.2×10−6). The v3_spacer exhibits the greatest signal-to-noise ratio. Data in f is displayed as mean with 95% CI. v1 (no Mg2+) Mean= 1.21, CI 0.96–1.46, sd 0.20; v1 (Mg2+) Mean= 2.54, CI 0.47–5.55, sd 1.21; v2 (no Mg2+) Mean= 3.60, CI 2.24–4.95, sd 1.29; v2 (Mg2+) Mean= 7.17, CI 6.23–8.11, sd 0.38; v3 (no Mg2+) Mean= 7.76, CI 4.49–11.02, sd 3.90; v3 (Mg2+) Mean= 5.73, CI 4.81–6.66, sd 0.74; v3_spacer (no Mg2+) Mean= 12.82, CI 10.86–14.78, sd 3.67; v3_spacer (Mg2+) Mean= 6.72, CI 5.22–8.22, sd 1.80; v3_control (no Mg2+) Mean= 3.43, CI 2.09–4.78, sd 0.84; v3_control (Mg2+) Mean= 7.34, CI 4.95–9.74, sd 2.59.
Extended Data Fig. 6 Background localizations are imager-sequence specific.
a, Accumulated-tPAINT or (b) sf-tPAINT surfaces were incubated with scrambled-imager and specific imager. c, Representative images compiled from 2000 frames of single molecule localization for accumulated-tPAINT surfaces and (d) sf-tPAINT probes incubated with 5 nM scrambled and specific imagers. The average localizations (µm−2s−1) were quantified at 2.5, 5, and 10 nM scrambled and specific imagers for (e) accumulated-tPAINT (n = 4 independent experiments) and (f) sf-tPAINT surfaces (n = 3 independent experiments). Localization density was computed for 5 regions per image to compute an average (black points). Mean ± standard deviation is noted above each category. Error bars are 95% CI. 2.5 nM (accumulated-tPAINT, Scrambled): Mean= 0.0040, 95% CI 0.0015–0.0066; 2.5 nM (accumulated-tPAINT, Specific): Mean= 0.045, 95% CI −0.0017–0.092; 5 nM (accumulated-tPAINT, Scrambled): Mean= 0.0077, 95% CI −0.0057–0.02101; 5 nM (accumulated-tPAINT, Specific): Mean= 0.086, 95% CI −0.0032–0.17; 10 nM (accumulated-tPAINT, Scrambled): Mean= 0.0061, 95% CI 0.0025–0.0097; 10 nM (accumulated-tPAINT, Specific): Mean= 0.17, 95% CI −0.020–0.36; 2.5 nM (sf-tPAINT, Scrambled): Mean= 0.0024, 95% CI 0.00057–0.0043; 2.5 nM (sf-tPAINT, Specific): Mean= 0.022, 95% CI 0.0094–0.034; 5 nM (sf-tPAINT, Scrambled): Mean= 0.0035, 95% CI 0.0011–0.0059; 5 nM (sf-tPAINT, Specific): Mean= 0.028, 95% CI 0.0041–0.051; 10 nM (sf-tPAINT, Scrambled): Mean= 0.0037, 95% CI 0.0024–0.0050; 10 nM (sf-tPAINT, Specific): Mean= 0.044, 95% confidence interval −0.0048–0.094. Data were compared via a 2-way ANOVA. For localization on accumulated-tPAINT probe surface: 2.5 nM scramble versus 2.5 specific (p = 0.9968); 5 nM scramble versus 5 nM specific (p = 0.7527); 10 nM scramble is statistically different than 10 nM specific (p = 0.0115). For localization on sf-tPAINT probe surface: 2.5 nM scramble versus 2.5 specific (p = 0.3153); 5 nM scramble versus 5 nM specific (p = 0.1051); 10 nM scramble is statistically different than 10 nM specific (p = 0.0023).
Extended Data Fig. 7 Schematic showing the filtering algorithm and effect of filtering on representative data.
a, First, tPAINT data was subjected to kinetic and density-based filtering prior to analysis. Kinetic filtering was accomplished via a 25-frame moving window of time traces of localizations within 35 nm oversampled pixels. If 14 events occurred within the 25-frame window (corresponding to 2.8 s of accumulated single molecule bond lifetime), all the component events were removed. Second, a Voronoi-tessellation assigned a polygon, comprised of all points closer to that localization than to any other localization, to each tPAINT localization. A local “density” was computed for each localization. Localizations with density lower than 2x, 5x, or 10x the background density were removed to produce the final tPAINT image. b, Demonstration of how increasingly stringent density filters (2x, 5x, 10x, and 15x the background localization density) affects the tPAINT signal. In the overlay, red points indicate localization density that has been removed by the density filter while white regions indicate localizations that passed the density threshold. The high zoom overlay displays the raw localizations as points, not gaussians. At the highest density-based filter settings, localizations on the edge of the filopodial extension are removed (high zoom overlay, 10x and 15x density filter). Scale bars: whole image view, 5 μm; platelet zoom view, 1 μm; high zoom view; 500 nm. The processing described in (a, b) above were applied to all tPAINT data reported in this manuscript: platelets sf-tPAINT n = 3 independent experiments, 3 donors, 8 images; fibroblasts n = 4 experiments, 10 images; accumulated-tPAINT platelets, n = 8 replicates, 3 donors, 22 images; n = 9 replicates, 24 images.
Extended Data Fig. 8 Cellular tension feature dimensions depend on the imaging window in sf-tPAINT.
a, Live-cell sf-tPAINT imaging of platelet tension displayed using different time windows (ranging from 50 sec to 1000 sec). The apparent length or width of cellular tension features depends on the number of frames that are integrated to produce a super-resolved image. To demonstrate this point, we rendered the lamellipodial edge of 3 human platelets (from n = 3 independent experiments, 2 platelets shown) and measured the apparent width of the lamellipodial edge tension ring as tPAINT data is integrated over various time windows. Super-resolved tPAINT images were rendered as greyscale images, and ring width was measured via linescan analysis (black dots). The data were fit to a gaussian via Matlab’s curvefitting tool (blue line). The measured FWHM of the fitted gaussians depends on the number of frames integrated to produce the super-resolved tPAINT image. b, Plot showing that the localization density generally increased with increasing number of integrated frames. Each colored line shows a unique ROI. c, Plot showing the relation between the FWHM of the tension ring and the number of integrated frames. The data shown are from 3 human platelets from n = 3 independent experiments (2 linescans per platelet). In principle, it is desirable to use the minimum number of frames possible to render an image in order to minimize feature blurring due to cellular dynamics during the imaging window; however, image quality decreases, with localizations becoming more punctate, when fewer frames are integrated. To produce high-quality tPAINT images, these considerations must both be balanced. All scale bars are 2 μm.
Extended Data Fig. 9 Collage of examples showing sf-tPAINT of human platelets treated with cytoskeletal inhibitors.
a, Time-resolved 8.5 pN tPAINT of platelets pre-treated with 50 μM CK666 for 30 min before being seeded on sf-tPAINT probes. b, Time-resolved 8.5 pN tPAINT image of platelet before and after treatment with 10μM ML-7 (MLCK inhibitor). c, Representative examples of images for cells treated with inhibitors displayed with a 5x density filter and kinetic filter. Human platelets treated with vehicle (DMSO) as control (n = 3 independent experiments), human platelets treated with CK666 (50 μM) after being seeded on the surface (n = 2 independent experiments), human platelets pretreated with CK666 (50 μM) for 30 min before being seeded on the surface (n = 3 independent experiments), human platelets treated with ML-7 (MLCK inhibitor, 10 μM) after being seeded on the surface (n = 3 independent experiments). Three examples are shown for each condition.
Extended Data Fig. 10 Surface density of tPAINT probes on the coverslip.
a, DNA-PAINT imaging of docking site coated surfaces (500 pM Cy3B-imager, 150,000–200,000 frames). Intensity-based peakfinding identified localization clusters (red dots). b, Histogram of nearest-neighbor distances reveals average cluster-cluster distance of 43 nm. c, Alternate DBSCAN clustering algorithm (20 localization minimum, 0.05 pixel search radius) identified clusters (displayed as colored dots). d, Nearest-neighbor histogram of the centroids of the clusters identified in c reports 55 nm average nearest-neighbor distance. Images in a and c are representative of n = 3 independent experiments. e-h, Variations in cluster localization density suggested peakfinding/DBSCAN did not identify individual docking sites. To count individual docking sites, we performed quantitative-PAINT (qPAINT). e, Calibration DNA origami used for calculating imager influx rate and (f) DNA-PAINT image of origami. Images were acquired at 1, 2.5, and 5 nM Cy3B imager (n = 3 independent experiments). Plot depicts cumulative distribution function of dark times between imager binding (red) and exponential fit (blue) for selected origamis (yellow circles). This analysis calculated kon as 1.2×106 M−1s−1. g, h, qPAINT of tPAINT surface reveal dense, heterogeneous clusters of docking sites on the surface (i–l). Quantitative measurements of the surface density of probes were performed to supplement qPAINT and clustering measurements. i, j, Fluorescence intensity versus concentration for Texas-red (TR) tagged phospholipid vesicles (5 measurements per concentration per experiment, n = 3 independent experiments), and soluble Cy3B-DNA (5 measurements per concentration per experiment, n = 2 independent experiments). Error bars are standard deviation. k, F factor calibration (ratio of TR:Cy3B fluorescence). Error bars calculated from the propagated standard deviation of Cy3B-DNA/TR-DHPE measurements. l, To calculate tPAINT probe density, fluorescence measurements of Cy3B-DNA tPAINT surfaces (5 measurements from each of n = 3 independent experiments) were converted into density via the F factor. tPAINT probe density is 2364 + /−255 probes per square micron (mean + /-propagated SEM from Cy3B and TR measurements).
Supplementary information
Supplementary Information
Supplementary Figs. 1–9, Tables 1–4 and Notes 1–3.
Supplementary Video 1
Raw, unprocessed single molecule localizations corresponding to 60 s of the sf-tPAINT platelet experiment data. A small region of this data is displayed in Fig. 1c–e. Note that the colormap in this video is scaled to enable visualization of the single molecule localizations. The bright objects are TetraSpeck beads, which served as fiducial markers for drift correction. The video playback speed is real time (5 Hz).
Supplementary Video 2
Raw, unprocessed single molecule localizations corresponding to 60 s of the accumulated-tPAINT platelet experiment data. A small region of this data is displayed in Fig. 3b–f. Note that the colormap in this video is scaled to enable visualization of the single molecule localizations. The bright objects are TetraSpeck beads, which served as fiducial markers for drift correction. The video playback speed is real time (5 Hz).
Rights and permissions
About this article
Cite this article
Brockman, J.M., Su, H., Blanchard, A.T. et al. Live-cell super-resolved PAINT imaging of piconewton cellular traction forces. Nat Methods 17, 1018–1024 (2020). https://doi.org/10.1038/s41592-020-0929-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41592-020-0929-2