Abstract
This paper describes outcomes of the 2019 Cryo-EM Model Challenge. The goals were to (1) assess the quality of models that can be produced from cryogenic electron microscopy (cryo-EM) maps using current modeling software, (2) evaluate reproducibility of modeling results from different software developers and users and (3) compare performance of current metrics used for model evaluation, particularly Fit-to-Map metrics, with focus on near-atomic resolution. Our findings demonstrate the relatively high accuracy and reproducibility of cryo-EM models derived by 13 participating teams from four benchmark maps, including three forming a resolution series (1.8 to 3.1 Å). The results permit specific recommendations to be made about validating near-atomic cryo-EM structures both in the context of individual experiments and structure data archives such as the Protein Data Bank. We recommend the adoption of multiple scoring parameters to provide full and objective annotation and assessment of the model, reflective of the observed cryo-EM map density.
Similar content being viewed by others
Main
Cryo-EM has emerged as a key method to visualize and model biologically important macromolecules and cellular machines. Researchers can now routinely achieve resolutions better than 4 Å, yielding new mechanistic insights into cellular processes and providing support for drug discovery1.
The recent explosion of cryo-EM structures raises important questions. What are the limits of interpretability given the quality of maps and resulting models? How can model accuracy and reliability be quantified under the simultaneous constraints of map density and chemical rules?
The EMDataResource Project (EMDR) (emdataresource.org) aims to derive validation methods and standards for cryo-EM structures through community consensus2. EMDR has convened an EM Validation Task Force3 analogous to those for X-ray crystallography4 and NMR5 and has sponsored challenges, workshops and conferences to engage cryo-EM experts, modelers and end-users2,6. During this period, cryo-EM has evolved rapidly (Fig. 1).
a, Plot of reported resolution versus PDB release year. Models derived from single particle cryo-EM maps have increased dramatically since the ‘resolution revolution’ circa 2014. Higher-resolution structures (blue bars) are also trending upward. b, EMDataResource challenge activities timeline.
This paper describes outcomes of EMDR’s most recent challenge, the 2019 Model ‘Metrics’ Challenge. Map targets representing the state-of-the-art in cryo-EM single particle reconstruction were selected in the near-atomic resolution regime (1.8–3.1 Å) with a twist: three form a resolution series from the same specimen/imaging experiment. Careful evaluation of submitted models by participating teams leads us to several specific recommendations for validating near-atomic cryo-EM structures, directed toward both individual researchers and the Protein Data Bank (PDB) structure data archive7.
Results
Challenge design
Challenge targets (Fig. 2) consisted of a three-map human heavy-chain apoferritin (APOF) resolution series (a 500-kDa octahedral complex of 24 ɑ-helix-rich subunits), with maps differing only in the number of particles used in reconstruction8, plus a single map of horse liver alcohol dehydrogenase (ADH) (an 80-kDa ɑ/β homodimer with NAD and Zn ligands)9.
Shown from left to right are ɑ-helix-rich APOF at 1.8, 2.3 and 3.1 Å (EMDB entries EMD-20026, EMD-20027 and EMD-20028) and ADH at 2.9 Å (EMDB entry EMD-0406). a, Full maps for each target. b,c, Representative secondary structural elements (APOF, residues 14–42; ADH, residues 34–45) with masked density for protein backbone atoms only (b), and for all protein atoms (c). Visible map features transition from near-atomic to secondary -structure dominated over the 1.8–3.1 Å resolution range. d, EMDB maps used in model Fit-to-Map analysis (APOF targets, masked single subunits; ADH, unmasked sharpened map). The molecular boundary is shown in red at the EMDB recommended contour level, background noise is represented in gray at one-third of the EMDB recommended contour level and the full map extent is indicated by the black outline.
A key criterion for target selection was availability of high-quality, experimentally determined model coordinates to serve as references (Fig. 3a). A 1.5 Å X-ray structure10 served as the APOF reference since no cryo-EM model was available. The X-ray model provides an excellent although not a fully optimized fit to each map, owing to method/sample differences. For ADH, the structure deposited by the original cryo-EM study authors served as the reference9.
a–c, Overview of the challenge setup (a), submissions (b) and evaluation (c) strategy. d, Scores comparison. Multiple interactive tabular and graphical displays enable comparative evaluations (model-compare.emdataresource.org). Top, Map-Model FSC curves, APOF 1.8 Å models (random light colors) versus reference model (bold cherry red). Map-Model FSC measures overall agreement of the experimental density map with a density map derived from the coordinate model (model map)12. Curves are calculated from Fourier coefficients of the two maps and plotted versus frequency (resolution−1). The resolution value corresponding to FSC = 0.5 (black horizontal line) is typically reported. Smaller values indicate better fit. Bottom, scores comparison tool, ADH models. Interactive score distribution sliders reveal at a glance how well submitted models performed relative to each other. Parallel lanes display score distributions for each evaluated metric in a manner conceptually similar to the graphical display for key metrics used in wwPDB validation reports4,32. Score distributions are shown for four representative metrics, one from each evaluation track. Model scores are plotted horizontally (semi-transparent diamonds) with color coding to indicate worse (left, orange) and better (right, green) values. Darker, opaque diamonds indicate multiple overlapping scores. Scores for two individual models are also highlighted: the interactive display enables individual models to be identified and compared (red and blue triangles).
Thirteen teams from the USA and Europe submitted 63 models in total, using whatever modeling software they preferred, yielding 15–17 submissions per target (Fig. 3b and Table 1). Most (51) were created ab initio, sometimes supported by additional manual steps, while others (12) were optimizations of publicly available models. The estimated human effort per model was 7 h on average, with a wide range (0–80 h).
Submitted models were evaluated as in the previous challenge11 with multiple metrics in each of four tracks: Fit-to-Map, Coordinates-only, Comparison-to-Reference and Comparison-among-Models (Fig. 3c). The metrics include many in common use as well as several recently introduced.
Metrics to evaluate global Fit-to-Map included Map-Model Fourier shell correlation (FSC)12, FSC average13, Atom Inclusion14, EMRinger15, density-based correlation scores from TEMPy16,17,18, Phenix19 and the recently introduced Q-score to assess atom resolvability8.
Metrics to evaluate overall Coordinates-only quality included Clashscore, Rotamer outliers and Ramachandran outliers from MolProbity20, as well as standard geometry measures (for example, bond, chirality, planarity) from Phenix21. PDB currently uses all of these validation measures based on community recommendations3,4,5. New to this challenge round was CaBLAM, which evaluates protein backbone conformation using virtual dihedral angles22.
Metrics assessing similarity of model to reference included Global Distance Test23, Local Difference Distance Test24, CaRMSD25 and Contact Area Difference26. Davis-QA was used to measure similarity among submitted models27. These measures are widely used in critical assessment of protein structure prediction (CASP) competitions27.
Several metrics were also evaluated per residue. These were Fit-to-Map: EMRinger15, Q-score8, Atom Inclusion14, SMOC18 and CCbox19; and for Coordinates-only: Clashes, Ramachandran outliers20 and CaBLAM22.
Evaluated metrics are tabulated with brief definitions in Table 2 and extended descriptions are provided in Methods.
An evaluation system website with interactive tables, plots and tools (Fig. 3d) was established to organize and enable analysis of the challenge results and make the results accessible to all participants (model-compare.emdataresource.org).
Overall and local quality of models
Most submitted models scored well, landing in ‘acceptable’ regions in each of the evaluation tracks, and in many cases performing better than the associated reference structure that served as a control (Supplementary Fig. 1). Teams that submitted ab initio models reported that additional manual adjustment was beneficial, particularly for the two lower resolution targets.
Evaluation exposed four fairly frequent issues: mis-assignment of peptide-bond geometry, misorientation of peptides, local sequence misalignment and failure to model associated ligands. Two-thirds of submitted models had one or more peptide-bond geometry errors (Extended Data Fig. 1).
At resolutions near 3 Å or in weak local density, the carbonyl O protrusion disappears into the tube of backbone density (Fig. 2), and trans peptide bonds are more readily modeled in the wrong orientation. If peptide torsion ϕ (C,N,Cα,C), ψ (N,Cα,C,N) values are explicitly refined, adjacent sidechains can be pushed further in the wrong direction. Such cases are not flagged as Ramachandran outliers but they are recognized by CaBLAM28 (Extended Data Fig. 2).
Sequence misthreadings misplace residues over very large distances. The misalignment can be recognized by local Fit-to-Map criteria, with ends flagged by CaBLAM, bad geometry, cis-nonPro peptides and clashes (Extended Data Fig. 3).
ADH contains tightly bound ligands: an NADH cofactor as well as two zinc ions per subunit, with one zinc in the active site and the other in a spatially separate site coordinated by four cysteine residues9. Models lacking these ligands had considerable local modeling errors, sometimes even mistracing the backbone (Extended Data Fig. 4).
Although there was evidence for ordered water in higher-resolution APOF maps8, only two groups elected to model water. Submissions were also split roughly 50/50 for (1) inclusion of predicted H-atom positions and (2) refinement of isotropic B factors. Although near-atomic cryo-EM maps do not have a sufficient level of detail to directly identify H-atom positions, inclusion of predicted positions can still be useful for identifying steric properties such as H-bonds or clashes20. Where provided, refined B factors modestly improved Fit-to-Map scores (Extended Data Fig. 5).
Evaluating metrics: Fit-to-Map
Score distributions of Fit-to-Map metrics (Table 2) were systematically compared (Fig. 4a–d). For APOF, single subunits were evaluated against masked subunit maps, whereas for ADH, dimeric models were evaluated against the full sharpened cryo-EM map (Fig. 2d). To control for the varied impact of H-atom inclusion or isotropic B-factor refinement on different metrics, all evaluated scores were produced with H atoms removed and all B factors were set to zero.
Model metrics (Table 2) were compared with each other to assess how similarly they performed in scoring the challenge models. a–d, Fit-to-Map metrics analyses. a, Pairwise correlations of scores for all models across all map targets (n = 63). b, Average correlation of scores per target (average over four correlation coefficients, one for each map target with T1, n = 16; T2, n = 15; T3, n = 15; T4, n = 17). Correlation-based metrics are identified by bold labels. In a, table order is based on a hierarchical cluster analysis (Methods). Three red-outlined boxes along the table diagonal correspond to identified clusters (no. c1–c3). For ease of comparison, order in b is identical to a. c, Representative score distributions are plotted by map target, ordered by map target resolution (see legend at bottom; T1, n = 16; T2, n = 15; T4, n = 17; T3, n = 15). Each row represents one of the three clusters defined in (a). Each score distribution is represented in box-and-whisker format (left) along with points for each individual score (right). Lower boxes represent Q1–Q2 (25th–50th percentile, in target color as shown in legend); upper boxes represent Q2–Q3 (25th–75th percentile, dark gray). Boxes do not appear when quartile limits are identical. Whiskers span 10th to 90th percentile. To improve visualization of closely clustered scores, individual scores (y values) are plotted against slightly dithered x values. d, Scores for one representative pair of metrics are plotted against each other (CCbox from cluster 1 and Q-score from Cluster 2). Diagonal lines represent linear fits by map target. e, Coordinates-only metrics comparison. f, Fit-to-Map, Coordinates-only and Comparison-to-Reference metrics comparison. Correlation levels in a,b,e,f are indicated by shading (see legend at top). See the Methods for additional details.
Score distributions were first evaluated for all 63 models across all four challenge targets. A wide diversity in performance was observed, with poor correlations between most metrics (Fig. 4a). This means that a model that scored well relative to all 62 others using one metric may have a much poorer ranking using another. Hierarchical analysis identified three distinct clusters of similarly performing metrics (Fig. 4a, labels c1–c3).
The unexpected sparse correlations and clustering can be understood by considering per-target score distribution ranges, which differ substantially from each other. The three clusters identify sets of metrics that share similar trends (Fig. 4c).
Cluster 1 metrics (Fig. 4c, top row) share the trend of decreasing score values with increasing map resolution. The cluster consists of six real-space correlation measures, three from TEMPy16,17,18 and three from Phenix19. Each evaluates a model’s fit in a similar way: by correlating calculated model-map density with experimental map density. In most cases (five out of six), correlation is performed after model-based masking of the experimental map. This observed trend is contrary to the expectation that a Fit-to-Map score should increase as resolution improves. The trend arises at least in part because map resolution is an explicit input parameter for this class of metrics. For a fixed map/model pair, changing the input resolution value will change the score. As map resolution increases, the level of detail that a model-map must faithfully replicate to achieve a high correlation score must also increase.
Cluster 2 metrics (Fig. 4c, middle row) share the inverse trend: score values improve with increasing map target resolution. Cluster 2 metrics consist of Phenix Map-Model FSC = 0.5 (ref. 19), Q-score8 and EMRinger15. The observed trend is expected: by definition, each metric assesses a model’s fit to the experimental map in a manner that is intrinsically sensitive to map resolution. In contrast with cluster 1, cluster 2 metrics do not require map resolution to be supplied as an input parameter.
Cluster 3 metrics (Fig. 4c, bottom row) share a different overall trend: score values are substantially lower for ADH relative to APOF map targets. These measures include three unmasked correlation functions from TEMPy16,17,18, Refmac FSCavg13, Electron Microscopy Data Bank (EMDB) Atom Inclusion14 and TEMPy ENV16. All of these measures consider the full experimental map without masking, so can be sensitive to background noise, which is substantial in the unmasked ADH map and minimal in the masked APOF maps (Fig. 2d).
Score distributions were also evaluated for how similarly they performed per target, and in this case most metrics were strongly correlated with each other (Fig. 4b). This means that for any single target, a model that scored well relative to all others using one metric also fared well using nearly every other metric. This situation is illustrated by comparing scores for two different metrics, CCbox from cluster 1 and Q-score from cluster 2 (Fig. 4d). The plot’s four diagonal lines demonstrate that the scores are tightly correlated with each other within each map target. But, as described above, the two metrics have different sensitivities to map-specific factors. It is these different sensitivities that give rise to the separated, parallel spacings of the four diagonal lines, indicating score ranges on different relative scales.
One Fit-to-Map metric showed poor per-target correlation with all others: TEMPy ENV (Fig. 4b). ENV evaluates atom positions relative to a density threshold that is based on sample molecular weight. At near-atomic resolution this threshold is overly generous. TEMPy Mutual Information and EMRinger also diverged from others (Fig. 4b). Mutual information scores reflected strong influence of ADH background noise. In contrast, masked MI_OV correlated well with other measures. EMRinger yielded distinct distributions owing to its focus on backbone placement15.
Collectively these results reveal that multiple factors such as using experimental map resolution as an input parameter, presence of background noise and density threshold selection can strongly affect Fit-to-Map score values, depending on the chosen metric. These are not desirable features for archive-wide validation of deposited cryo-EM structures.
Evaluating metrics: Coordinates-only and versus Reference
Metrics to assess model quality based on Coordinates-only (Table 2), as well as Comparison-to-Reference and Comparison-among-Models (Table 2) were also evaluated and compared (Fig. 4e,f).
Most Coordinates-only metrics were poorly correlated with each other (Fig. 4e), with the exception of bond, bond angle and chirality root mean squared deviation (r.m.s.d.), which form a small cluster. Ramachandran outliers, widely used to validate protein backbone conformation, were poorly correlated with all other Coordinates-only measures. More than half (33) of submitted models had zero Ramachandran outliers, while only four had zero CaBLAM conformation outliers. Ramachandran statistics are increasingly used as restraints29,30, which reduces their use as a validation metric. These results support the concept of CaBLAM as an informative score for validating backbone conformation22.
CaBLAM metrics, while orthogonal to other Coordinates-only measures, were unexpectedly found to perform very similarly to Comparison-to-Reference metrics. The similarity likely arises because the worst modeling errors in this challenge were sequence and backbone conformation mis-assignments. These errors were equally flagged by CaBLAM, which compares models against statistics from high-quality PDB structures, and the Comparison-to-Reference metrics, which compare models against a high-quality reference. To a lesser extent, modeling errors were also flagged by Fit-to-Map metrics (Fig. 4f). Overall, Coordinates-only metrics were poorly correlated with Fit-to-Map metrics (Fig. 4f and Extended Data Fig. 6a).
Protein sidechain accuracy is specifically assessed by Rotamer and GDC-SC, while EMRinger, Q-score, CAD, hydrogen bonds in residue pairs (HBPR > 6), GDC and LDDT metrics include sidechain atoms. For these eight measures, Rotamer was completely orthogonal, Q-score was modestly correlated with the Comparison-to-Reference metrics, and EMRinger, which measures sidechain fit as a function of main chain conformation, was largely independent (Fig. 4f). These results suggest a need for multiple metrics (for example, Q-score, EMRinger, Rotamer) to assess different aspects of sidechain quality.
Evaluating metrics: local scoring
Several residue-level scores were calculated in addition to overall scores. Five Fit-to-Map metrics considered masked density for both map and model around the evaluated residue (CCbox19, SMOC18), density profiles at nonhydrogen atom positions (Q-score8), density profiles of nonbranched residue Cɣ-atom ring paths (EMRinger15) or density values at non-H-atom positions relative to a chosen threshold (Atom Inclusion14). In two of these five, residue-level scores were obtained as sliding-window averages over multiple contiguous residues (SMOC, nine residues; EMRinger, 21 residues).
Residue-level correlation analyses similar to those described above (not shown) indicate that local Fit-to-Map scores diverged more than their corresponding global scores. Residue-level scoring was most similar across evaluated metrics for high resolution maps. This observation suggests that the choice of method for scoring residue-level fit becomes less critical at higher resolution, where maps tend to have stronger density/contrast around atom positions.
A case study of a local modeling error (Extended Data Fig. 3) showed that Atom Inclusion14, CCbox19 and Q-score8 produced substantially worse scores within a four-residue ɑ-helical misthread relative to correctly assigned flanking residues. In contrast, the sliding-window-based metrics were largely insensitive (a new TEMPy version offers single residue (SMOCd) and adjustable window analysis (SMOCf)31). At near-atomic resolution, single residue Fit-to-Map evaluation methods are likely to be more useful.
Residue-level Coordinates-only, Comparison-to-Reference and Comparison-among-Models metrics (not shown) were also evaluated for the same modeling error. The MolProbity server20,22 flagged the problematic four-residue misthread via CaBLAM, cis-Peptide, Clashscore, bond and angle scores, but all Ramachandran scores were either favored or allowed. The Comparison-to-Reference LDDT and LGA local scores and the Davis-QA model consensus score also strongly flagged this error. The example demonstrates the value of combining multiple orthogonal measures to identify geometry issues, and further highlights the value of CaBLAM as an orthogonal measure for backbone conformation.
Group performance
Group performance was examined by modeling category and target by combining Z-scores from metrics determined to be meaningful in the analyses described above (Methods and Extended Data Fig. 6). A wide variety of map density features and algorithms were used to produce a model, and most were successful yet allowing a few mistakes, often in different places (Extended Data Figs. 1–4). For practitioners, it might be beneficial to combine models from several ab initio methods for subsequent refinement.
Discussion
This third EMDR Model Challenge has demonstrated that cryo-EM maps with a resolution ≤3 Å and from samples with limited conformational flexibility have excellent information content, and automated methods are able to generate fairly complete models from such maps, needing only small amounts of manual intervention.
Inclusion of maps in a resolution series enabled controlled evaluation of metrics by resolution, with a completely different map providing a useful additional control. These target selections enabled observation of important trends that otherwise could have been missed. In a recent evaluation of predicted models in the CASP13 competition against several roughly 3 Å cryo-EM maps, TEMPy and Phenix Fit-to-Map correlation measures performed very similarly31. In this challenge, because the chosen targets covered a wider resolution range and had more variability in background noise, the same measures were found to have distinctive, map feature-sensitive performance profiles.
Most submitted models were overall either equivalent to or better than their reference model. This achievement reflects significant advances in the development of modeling tools relative to the state presented a decade ago in our first model challenge2. However, several factors beyond atom positions that become important for accurate modeling at near-atomic resolution were not uniformly addressed; only half included refinement of atomic displacement factors (B factors) and a minority attempted to fit water or bound ligands.
Fit-to-Map measures were found to be sensitive to different physical properties of the map, including experimental map resolution and background noise level, as well as input parameters such as density threshold. Coordinates-only measures were found to be largely orthogonal to each other and also largely orthogonal to Fit-to-Map measures, while Comparison-to-Reference measures were generally well correlated with each other.
The cryo-EM modeling community as represented by the challenge participants have introduced a number of metrics to evaluate models with sound biophysical basis. Based on our careful analyses of these metrics and their relationships, we make four recommendations regarding validation practices for cryo-EM models of proteins determined at near-atomic resolution as studied here between 3.1 and 1.8 Å, a rising trend for cryo-EM (Fig. 1a).
Recommendation 1. For researchers optimizing a model against a single map, nearly any of the evaluated global Fit-to-Map metrics (Table 2) can be used to evaluate progress because they are all largely equivalent in performance. The exception is TEMPy, ENV is more appropriate at lower resolutions (>4 Å).
Recommendation 2. To flag issues with local (per residue) Fit-to-Map, metrics that evaluate single residues are more suitable than those using sliding-window averages over multiple residues (Evaluating metrics: local scoring).
Recommendation 3. The ideal Fit-to-Map metric for archive-wide ranking will be insensitive to map background noise (appropriate masking or alternative data processing can help), will not require input of estimated parameters that affect score value (for example, resolution limit, threshold) and will yield overall better scores for maps with trustworthy higher-resolution features. The three cluster 2 metrics identified in this challenge (Fig. 4a ‘c2’ and Fig. 4c center row) meet these criteria.
-
Map-Model FSC12,19 is already in common use, and can be compared with the experimental map’s independent half-map FSC curve.
-
Global EMRinger score15 can assess nonbranched protein sidechains.
-
Q-score can be used both globally and locally for validating nonhydrogen atom x,y,z positions8.
Other Fit-to-Map metrics may be rendered suitable for archive-wide comparisons through conversion of raw scores to Z-scores over narrow resolution bins, as is currently done by the PDB for some X-ray-based metrics4,32.
Recommendation 4. CaBLAM and MolProbity cis-peptide detection22 are useful to detect protein backbone conformation issues. These are particularly valuable tools for cryo-EM, since maps at typical resolutions (2.5–4.0 Å, Fig. 1a) may not resolve backbone carbonyl oxygens (Fig. 2).
In this challenge, more time could be devoted to analysis when compared with previous rounds because infrastructure for model collection, processing and assessment is now established. However, several important issues could not be addressed, including evaluation of overfitting using half-map based methods13,33,34,35, effect of map sharpening on Fit-to-Map scores8,36, validation of ligand fit and metal ion/water identification and validation at atomic resolution including H atoms. EMDR plans to sponsor additional model challenges to continue promoting development and testing of cryo-EM modeling and validation methods.
Methods
Challenge process and organization
Informed by previous challenges2,6,11, the 2019 Model Challenge process was substantially streamlined in this round. In March, a panel of advisors with expertise in cryo-EM methods, modeling and/or model assessment was recruited. The panel worked with EMDR team members to develop the challenge guidelines, identify suitable map targets from EMDB and reference models from the PDB and recommend the metrics to be calculated for each submitted model.
The challenge rules and guidance were as follows: (1) ab initio modeling is encouraged but not required. For optimization studies, any publicly available coordinate set can be used as the starting model. (2) Regardless of the modeling method used, submitted models should be as complete and as accurate as possible (that is, equivalent to publication-ready). (3) For each target, a separate modeling process should be used. (4) Fitting to either the unsharpened/unmasked map or one of the half-maps is strongly encouraged. (5) Submission in mmCIF format is strongly encouraged.
Members of cryo-EM and modeling communities were invited to participate in mid-April 2019 and details were posted on the challenges website (challenges.emdataresource.org). Models were submitted by participant teams between 1 and 28 May 2019. For APOF targets, coordinate models were submitted as single subunits at the position of a provided segmented density consisting of a single subunit. ADH models were submitted as dimers. For each submitted model, metadata describing the full modeling workflow were collected via a Drupal webform, and coordinates were uploaded and converted to PDBx/mmCIF format using PDBextract51. Model coordinates were then processed for atom/residue ordering and nomenclature consistency using PDB annotation software (Feng Z., https://sw-tools.rcsb.org/apps/MAXIT) and additionally checked for sequence consistency and correct position relative to the designated target map. Models were then evaluated as described below (Model evaluation system).
In early June, models, workflows and initial calculated scores were made available to all participants for evaluation, blinded to modeler team identity and software used. A 2.5-day workshop was held in mid-June at Stanford/SLAC to review the results, with panel members attending in person. All modeling participants were invited to attend remotely and present overviews of their modeling processes and/or assessment strategies. Recommendations were made for additional evaluations of the submitted models as well as for future challenges. Modeler teams and software were unblinded at the end of the workshop. In September, a virtual follow-up meeting with all participants provided an overview of the final evaluation system after implementation of recommended updates.
Coordinate sources and modeling software
Modeling teams created ab initio models or optimized previously known models available from the PDB. Models optimized against APOF maps used PDB entries 2fha, 5n26 or 3ajo as starting models. Models optimized against ADH used PDB entries 1axe, 2jhf or 6nbb. Ab initio software included ARP/wARP41, Buccaneer37, Cascaded-CNN46, Mainmast45, Pathwalker49 and Rosetta40. Optimization software included CDMD39, CNS52, DireX43, Phenix21, REFMAC13, MELD48, MDFF44 and reMDFF47. Participants made use of VMD53, Chimera38, COOT29 and PyMol for visual evaluation and/or manual model improvement of map-model fit. See Table 1 for software used by each modeling team. Modeling software versions/websites are listed in the Nature Research Reporting Summary.
Model evaluation system
The evaluation system for 2019 challenge (model-compare.emdataresource.org) was built on the basis of the 2016/2017 Model Challenge system11, updated with several additional evaluation measures and analysis tools. Submitted models were evaluated for >70 individual metrics in four tracks: Fit-to-Map, Coordinates-only, Comparison-to-Reference and Comparison-among-Models. A detailed description of the updated infrastructure and each calculated metric is provided as a help document on the model evaluation system website. Result data are archived at Zenodo54. Analysis software versions/websites are listed in the Nature Research Reporting Summary.
For brevity, a representative subset of metrics from the evaluation website are discussed in this paper. The selected metrics are listed in Table 2 and are further described below. All scores were calculated according to package instructions using default parameters.
Fit-to-Map
The evaluated metrics included several ways to measure the correlation between map and model density as implemented in TEMPy16,17,18 v.1.1 (CCC, CCC_OV, SMOC, LAP, MI, MI_OV) and the Phenix21 v.1.15.2 map_model_cc module19 (CCbox, CCpeaks, CCmask). These methods compare the experimental map with a model map produced on the same voxel grid, integrated either over the full map or over selected masked regions. The model-derived map is generated to a specified resolution limit by inverting Fourier terms calculated from coordinates, B factors and atomic scattering factors. Some measures compare density-derived functions instead of density (MI, LAP16).
The Q-score (MAPQ v.1.2 (ref. 8) plugin for UCSF Chimera38 v.1.11) uses a real-space correlation approach to assess the resolvability of each model atom in the map. Experimental map density is compared to a Gaussian placed at each atom position, omitting regions that overlap with other atoms. The score is calibrated by the reference Gaussian, which is formulated so that a highest score of 1 would be given to a well-resolved atom in a map at an approximately 1.5 Å resolution. Lower scores (down to −1) are given to atoms as their resolvability and the resolution of the map decreases. The overall Q-score is the average value for all model atoms.
Measures based on Map-Model FSC curve, Atom Inclusion and protein sidechain rotamers were also compared. Phenix Map-Model FSC is calculated using a soft mask and is evaluated at FSC = 0.5 (ref. 19). REFMAC FSCavg13 (module of CCPEM42) integrates the area under the Map-Model FSC curve to a specified resolution limit13. EMDB Atom Inclusion determines the percentage of atoms inside the map at a specified density threshold14. TEMPy ENV is also threshold-based and penalizes unmodeled regions16. EMRinger (module of Phenix) evaluates backbone positioning by measuring the peak positions of unbranched protein Cγ atom positions versus map density in ring paths around Cɑ–Cβ bonds15.
Coordinates-only
Standard measures assessed local configuration (bonds, bond angles, chirality, planarity, dihedral angles; Phenix model statistics module), protein backbone (MolProbity Ramachandran outliers20; Phenix molprobity module) and sidechain conformations, and clashes (MolProbity rotamers outliers and Clashscore20; Phenix molprobity module).
New in this challenge round is CaBLAM22 (part of MolProbity and as Phenix cablam module), which uses two procedures to evaluate protein backbone conformation. In both cases, virtual dihedral pairs are evaluated for each protein residue i using Cɑ positions i − 2 to i + 2. To define CaBLAM outliers, the third virtual dihedral is between the CO groups flanking residue i. To define Calpha-geometry outliers, the third parameter is the Cɑ virtual angle at i. The residue is then scored according to virtual triplet frequency in a large set of high-quality models from PDB22.
Comparison-to-Reference and Comparison-among-Models
Assessing the similarity of the model to a reference structure and similarity among submitted models, we used metrics based on atom superposition (LGA GDT-TS, GDC and GDC-SC scores23 v.04.2019), interatomic distances (LDDT score24 v.1.2), and contact area differences (CAD26 v.1646). HBPLUS50 was used to calculate nonlocal hydrogen bond precision, defined as the fraction of correctly placed hydrogen bonds with more than six separations in sequence (HBPR > 6). DAVIS-QA determines for each model the average of pairwise GDT-TS scores among all other models27.
Local (per residue) scores
Residue-level visualization tools for comparing the submitted models were also provided for the following metrics: Fit-to-Map, Phenix CCbox, TEMPy SMOC, Q-score, EMRinger and EMDB Atom Inclusion; Comparison-to-Reference, LGA and LDDT; and Comparison-among-Models, DAVIS-QA.
Metric score pairwise correlations and distributions
For pairwise comparisons of metrics, Pearson correlation coefficients (P) were calculated for all model scores and targets (n = 63). For average per-target pairwise comparisons of metrics, P values were determined for each target and then averaged. Metrics were clustered according to the similarity score (1 − |P|) using a hierarchical algorithm with complete linkage. At the beginning, each metric was placed into a cluster of its own. Clusters were then sequentially combined into larger clusters, with the optimal number of clusters determined by manual inspection. In the Fit-to-Map evaluation track, the procedure was stopped after three divergent score clusters were formed for the all-model correlation data (Fig. 4a), and after two divergent clusters were formed for the average per-target clustering (Fig. 4b).
Controlling for model systematic differences
As initially calculated, some Fit-to-Map scores had unexpected distributions, owing to differences in modeling practices among participating teams. For models submitted with all atom occupancies set to zero, occupancies were reset to one and rescored. In addition, model submissions were split approximately 50/50 for each of the following practices: (1) inclusion of hydrogen atom positions and (2) inclusion of refined B factors. For affected fit-to-map metrics, modified scores were produced excluding hydrogen atoms and/or setting B factors to zero. Both original and modified scores are provided at the web interface. Only modified scores were used in the comparisons described here.
Evaluation of group performance
Rating of group performance was done using the group ranks and model ranks (per target) tools on the challenge evaluation website. These tools permit users, either by group or for a specified target and for all or a subcategory of models (for example, ab initio), to calculate composite Z-scores using any combination of evaluated metrics with any desired relative weightings. The Z-scores for each metric are calculated from all submitted models for that target (n = 63). The metrics (weights) used to generate composite Z-scores were as follows.
Coordinates-only
CaBLAM outliers (0.5), Calpha-geometry outliers (0.3) and Clashscore (0.2). CaBLAM outliers and Calpha-geometry outliers had the best correlation with Comparison-to-Reference parameters (Fig. 4f), and Clashscore is an orthogonal measure. Ramachandran and rotamer criteria were excluded since they are often restrained in refinement and are zero for many models.
Fit-to-Map
EMRinger (0.3), Q-score (0.3), Atom Inclusion (0.2) and SMOC (0.2). EMRinger and Q-score were among the most promising model-to-map metrics, and the other two provide distinct measures.
Comparison-to-Reference
LDDT (0.9), GDC_all (0.9) and HBPR >6 (0.2). LDDT is superposition-independent and local, while GDC_all requires superposition; H-bonding is distinct. Metrics in this category are weighted higher, because although the reference models are not perfect, they are a reasonable estimate of the right answer.
Composite Z-scores by metric category (Extended Data Fig. 6a) used the Group Ranks tool. For ab initio rankings (Extended Data Fig. 6b), Z-scores were averaged across each participant group on a given target, and further averaged across T1 + T2 and across T3 + T4 to yield overall Z-scores for high and low resolutions group 54 models were rated separately because they used different methods. Group 73’s second model on target T4 was not rated because the metrics are not set up to meaningfully evaluate an ensemble. Other choices of metric weighting schemes were tried, with very little effect on clustering.
Molecular graphics
Molecular graphics images were generated using UCSF Chimera38 (Fig. 2 and Extended Data Fig. 3) and KiNG55 (Extended Data Figs. 1, 2 and 4).
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The map targets used in the challenge were downloaded from the EMDB, entries EMD-20026 (file emd_20026_additional_1.map.gz), EMD-20027 (file emd_20027_additional_2.map.gz), EMD-20028 (file emd_20028_additional_2.map.gz) and EMD-0406 (file emd_0406.map.gz). Reference models were downloaded from the PDB, entries 3ajo and 6nbb. Submitted models, model metadata, result logs and compiled data are archived at Zenodo at https://doi.org/10.5281/zenodo.4148789, and at https://model-compare.emdataresource.org/data/2019/. Interactive summary tables, graphical views and .csv downloads of compiled results are available at https://model-compare.emdataresource.org/2019/cgi-bin/index.cgi. Source data are provided with this paper.
References
Mitra, A. K. Visualization of biological macromolecules at near-atomic resolution: cryo-electron microscopy comes of age. Acta Cryst. F 75, 3–11 (2019).
Lawson, C. L., Berman, H. M. & Chiu, W. Evolving data standards for cryo-EM structures. Struct. Dyn. 7, 014701 (2020).
Henderson, R. et al. Outcome of the first electron microscopy validation task force meeting. Structure 20, 205–214 (2012).
Read, R. J. et al. A new generation of crystallographic validation tools for the Protein Data Bank. Structure 19, 1395–1412 (2011).
Montelione, G. T. et al. Recommendations of the wwPDB NMR Validation Task Force. Structure 21, 1563–1570 (2013).
Lawson, C. L. & Chiu, W. Comparing cryo-EM structures. J. Struct. Biol. 204, 523–526 (2018).
wwPDB Consortium. Protein Data Bank: the single global archive for 3D macromolecular structure data. Nucleic Acids Res. 47, D520–D528 (2019).
Pintilie, G. et al. Measurement of atom resolvability in cryo-EM maps with Q-scores. Nat. Methods 17, 328–334 (2020).
Herzik, M. A. Jr, Wu, M. & Lander, G. C. High-resolution structure determination of sub-100 kDa complexes using conventional cryo-EM. Nat. Commun. 10, 1032 (2019).
Masuda, T., Goto, F., Yoshihara, T. & Mikami, B. The universal mechanism for iron translocation to the ferroxidase site in ferritin, which is mediated by the well conserved transit site. Biochem. Biophys. Res. Commun. 400, 94–99 (2010).
Kryshtafovych, A., Adams, P. D., Lawson, C. L. & Chiu, W. Evaluation system and web infrastructure for the second cryo-EM Model Challenge. J. Struct. Biol. 204, 96–108 (2018).
Rosenthal, P. B. & Henderson, R. Optimal determination of particle orientation, absolute hand, and contrast loss in single-particle electron cryomicroscopy. J. Mol. Biol. 333, 721–745 (2003).
Brown, A. et al. Tools for macromolecular model building and refinement into electron cryo-microscopy reconstructions. Acta Cryst. D 71, 136–153 (2015).
Lagerstedt, I. et al. Web-based visualisation and analysis of 3D electron-microscopy data from EMDB and PDB. J. Struct. Biol. 184, 173–181 (2013).
Barad, B. A. et al. EMRinger: side chain-directed model and map validation for 3D cryo-electron microscopy. Nat. Methods 12, 943–946 (2015).
Vasishtan, D. & Topf, M. Scoring functions for cryoEM density fitting. J. Struct. Biol. 174, 333–343 (2011).
Farabella, I. et al. TEMPy: a Python library for assessment of three-dimensional electron microscopy density fits. J. Appl. Crystallogr. 48, 1314–1323 (2015).
Joseph, A. P., Lagerstedt, I., Patwardhan, A., Topf, M. & Winn, M. Improved metrics for comparing structures of macromolecular assemblies determined by 3D electron-microscopy. J. Struct. Biol. 199, 12–26 (2017).
Afonine, P. V. et al. New tools for the analysis and validation of cryo-EM maps and atomic models. Acta Cryst. D 74, 814–840 (2018).
Chen, V. B. et al. MolProbity: all-atom structure validation for macromolecular crystallography. Acta Cryst. D 66, 12–21 (2010).
Liebschner, D. et al. Macromolecular structure determination using X-rays, neutrons and electrons: recent developments in Phenix. Acta Cryst. D 75, 861–877 (2019).
Williams, C. J. et al. MolProbity: more and better reference data for improved all-atom structure validation. Protein Sci. 27, 293–315 (2018).
Zemla, A. LGA: a method for finding 3D similarities in protein structures. Nucleic Acids Res. 31, 3370–3374 (2003).
Mariani, V., Biasini, M., Barbato, A. & Schwede, T. LDDT: a local superposition-free score for comparing protein structures and models using distance difference tests. Bioinformatics 29, 2722–2728 (2013).
Bertoni, M., Kiefer, F., Biasini, M., Bordoli, L. & Schwede, T. Modeling protein quaternary structure of homo- and hetero-oligomers beyond binary interactions by homology. Sci. Rep. 7, 10480 (2017).
Olechnovic, K., Kulberkyte, E. & Venclovas, C. CAD-score: a new contact area difference-based function for evaluation of protein structural models. Proteins 81, 149–162 (2013).
Kryshtafovych, A., Monastyrskyy, B. & Fidelis, K. CASP prediction center infrastructure and evaluation measures in CASP10 and CASP ROLL. Proteins 82, 7–13 (2014).
Prisant, M. G., Williams, C. J., Chen, V. B., Richardson, J. S. & Richardson, D. C. New tools in MolProbity validation: CaBLAM for CryoEM backbone, UnDowser to rethink ‘waters,’ and NGL Viewer to recapture online 3D graphics. Protein Sci. 29, 315–329 (2020).
Emsley, P., Lohkamp, B., Scott, W. G. & Cowtan, K. Features and development of Coot. Acta Cryst. D 66, 486–501 (2010).
Headd, J. J. et al. Use of knowledge-based restraints in phenix.refine to improve macromolecular refinement at low resolution. Acta Cryst. D 68, 381–390 (2012).
Kryshtafovych, A. et al. Cryo-electron microscopy targets in CASP13: overview and evaluation of results. Proteins 87, 1128–1140 (2019).
Gore, S. et al. Validation of structures in the Protein Data Bank. Structure 25, 1916–1927 (2017).
DiMaio, F., Zhang, J., Chiu, W. & Baker, D. Cryo-EM model validation using independent map reconstructions. Protein Sci. 22, 865–868 (2013).
Pintilie, G., Chen, D. H., Haase-Pettingell, C. A., King, J. A. & Chiu, W. Resolution and probabilistic models of components in cryoEM maps of mature P22 bacteriophage. Biophys. J. 110, 827–839 (2016).
Hryc, C. F. et al. Accurate model annotation of a near-atomic resolution cryo-EM map. Proc. Natl Acad. Sci. USA 114, 3103–3108 (2017).
Terwilliger, T. C., Sobolev, O. V., Afonine, P. V. & Adams, P. D. Automated map sharpening by maximization of detail and connectivity. Acta Cryst. D 74, 545–559 (2018).
Hoh, S., Burnley, T. & Cowtan, K. Current approaches for automated model building into cryo-EM maps using Buccaneer with CCP-EM. Acta Cryst. D 76, 531–541 (2020).
Pettersen, E. F. et al. UCSF Chimera–a visualization system for exploratory research and analysis. J. Comput. Chem. 25, 1605–1612 (2004).
Igaev, M., Kutzner, C., Bock, L. V., Vaiana, A. C. & Grubmuller, H. Automated cryo-EM structure refinement using correlation-driven molecular dynamics. eLife 8, https://doi.org/10.7554/eLife.43542 (2019).
Frenz, B., Walls, A. C., Egelman, E. H., Veesler, D. & DiMaio, F. RosettaES: a sampling strategy enabling automated interpretation of difficult cryo-EM maps. Nat. Methods 14, 797–800 (2017).
Chojnowski, G., Pereira, J. & Lamzin, V. S. Sequence assignment for low-resolution modelling of protein crystal structures. Acta Cryst. D 75, 753–763 (2019).
Burnley, T., Palmer, C. M. & Winn, M. Recent developments in the CCP-EM software suite. Acta Cryst. D 73, 469–477 (2017).
Wang, Z. & Schröder, G. F. Real-space refinement with DireX: from global fitting to side-chain improvements. Biopolymers 97, 687–697 (2012).
Trabuco, L. G., Villa, E., Mitra, K., Frank, J. & Schulten, K. Flexible fitting of atomic structures into electron microscopy maps using molecular dynamics. Structure 16, 673–683 (2008).
Terashi, G. & Kihara, D. De novo main-chain modeling for EM maps using MAINMAST. Nat. Commun. 9, 1618 (2018).
Si, D. et al. Deep learning to predict protein backbone structure from high-resolution cryo-EM density maps. Sci. Rep. 10, 4282 (2020).
Singharoy, A. et al. Molecular dynamics-based refinement and validation for sub-5 A cryo-electron microscopy maps. eLife 5, https://doi.org/10.7554/eLife.16105 (2016).
MacCallum, J. L., Perez, A. & Dill, K. A. Determining protein structures by combining semireliable data with atomistic physical models by Bayesian inference. Proc. Natl Acad. Sci. USA 112, 6985–6990 (2015).
Chen, M. & Baker, M. L. Automation and assessment of de novo modeling with Pathwalking in near atomic resolution cryoEM density maps. J. Struct. Biol. 204, 555–563 (2018).
McDonald, I. K. & Thornton, J. M. Satisfying hydrogen bonding potential in proteins. J. Mol. Biol. 238, 777–793 (1994).
Yang, H. et al. Automated and accurate deposition of structures solved by X-ray diffraction to the Protein Data Bank. Acta Cryst. D 60, 1833–1839 (2004).
Brünger, A. T. Version 1.2 of the crystallography and NMR system. Nat. Protoc. 2, 2728–2733 (2007).
Hsin, J., Arkhipov, A., Yin, Y., Stone, J. E. & Schulten, K. Using VMD: an introductory tutorial. Curr. Protoc. Bioinformatics 24, https://doi.org/10.1002/0471250953.bi0507s24 (2008).
Lawson, C. L. et al. 2019 EMDataresource model metrics challenge dataset. Zenodo https://doi.org/10.5281/zenodo.4148789 (2020).
Chen, V. B., Davis, I. W. & Richardson, D. C. KING (Kinemage, Next Generation): a versatile interactive molecular and scientific visualization program. Protein Sci. 18, 2403–2409 (2009).
Acknowledgements
EMDataResource (C.L.L., A.K., G.P., H.M.B. and W.C.) is supported by the US National Institutes of Health (NIH)/National Institute of General Medical Science, grant no. R01GM079429. The Singharoy team used the supercomputing resources of the Oak Ridge Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science at the Department of Energy under contract no. DE-AC05-00OR22725. The following additional grants are acknowledged for participant support: grant no. NIH/R35GM131883 to J.S.R. and C.W.; grant no. NIH/P01GM063210 to P.D.A., P.V.A., L.-W.H., J.S.R., T.C.T. and C.W.; National Science Foundation grant no. (NSF)/MCB-1942763 (CAREER) and NIH/R01GM095583 to A.S.; grant nos. NIH/R01GM123055, NIH/R01GM133840, NSF/DMS1614777, NSF/CMMI1825941, NSF/MCB1925643, NSF/DBI2003635 and Purdue Institute of Drug Discovery to D. Kihara; grant no. NIH/R01GM123159 to J.S.F.; Max Planck Society German Research Foundation grant no. IG 109/1-1 to M.I.; Max Planck Society German Research Foundation grant no. FOR-1805 to A.C.V.; grant nos. NIH/R37AI36040 and Welch Foundation/Q1279 to D. Kumar (PI: BVV Prasad); grant no. NSF/DBI2030381 to D. Si.; Medical Research Council grant no. MR/N009614/1 to T.B., C.M.P. and M.W.; Wellcome Trust grant no. 208398/Z/17/Z to A.P.J. and M.W.; Biotechnology and Biological Sciences Research Council grant no. BB/P000517/1 to K.C. and Biotechnology and Biological Sciences Research Council grant no. BB/P000975/1 to M.W.
Author information
Authors and Affiliations
Contributions
P.D.A., P.V.A., J.S.F., F.D.M., J.S.R., P.B.R., H.M.B., W.C., A.K., C.L.L., G.D.P. and M.F.S. formed the expert panel that selected targets, reference models and assessment metrics, set the challenge rules and attended the face-to-face results review workshop. K.Z. generated the APOF maps for the challenge. M.A.H. provided the published ADH map. C.L.L. designed and implemented the challenge model submission pipeline, and drafted the initial, revised and final manuscripts. Authors as listed in Table 1 built and submitted models and presented modeling strategies at the review workshop. A.K. designed and implemented the evaluation pipeline and website, and calculated scores. A.K., C.L.L., B.M., M.A.H., J.S.R., C.J.W., P.V.A. and J.S.F. analyzed models and model scores. A.P., Z.W., T.C.T., A.P.J., G.D.P., P.V.A. and C.J.W. contributed the software, and provided advice on use and scores interpretation. C.L.L., A.K., G.D.P. and J.S.R. drafted the figures. A.K., H.M.B., G.D.P., W.C., M.F.S., M.A.H. and J.S.R. contributed to manuscript writing. All authors reviewed and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
X.Y. is an employee of Janssen Research and Development. All other authors declare no competing interests.
Additional information
Peer review information Allison Doerr was the primary editor on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Evaluation of peptide bond geometry.
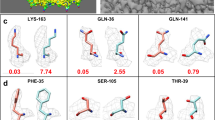
All 63 Challenge models were evaluated using MolProbity. APOF and ADH each have one cis peptide bond per subunit before a proline residue. (a) Counts of peptide bonds with each of the following conformational properties: cisP: cis peptide before proline, twistP: non-planar peptide (>30°) before proline, cis-nonP: cis peptide before non-proline, twist-nonP: non-planar peptide bond before non-proline. Incorrect cis-nonP usually occurred where the model was misfit (see Extended Data Figs. 2 and 3), while incorrect cis or trans Pro usually produced poor geometry. Values inconsistent with reference models are highlighted. Statistically, 1 in 20 proline residues are genuinely cis; only 1 in 3000 non-proline residues are genuinely cis, and strongly non-planar peptide bonds (>30°) are almost never genuine28. Models are identified by the submitting group (Gp #, group id as defined in Table 1), model number (some groups submitted multiple models), and Target (T1-T3: APOF, T4: ADH). Optimized models are shaded blue. Only two groups (28, 31) had all peptides correct for all 4 targets. Models illustrated in panels b-d are indicated by labeled boxes. (b) Correct cis peptide geometry for Pro A62 in two ADH models. (c) Incorrect trans peptide geometry, with huge clashes up to 1.25 Å overlap (clusters of hot pink spikes), 2 CaBLAM outliers (magenta CO dihedral lines), and poor density fit. (d) Incorrect trans peptide geometry, with huge 1.9 Å Cβ deviation at Leu 61 (magenta ball) because of incorrect hand of Cα, and 2 CaBLAM outliers. Molecular graphics were generated using KiNG.
Extended Data Fig. 2 Classic CaBLAM outlier with no Ramachandran outlier.
a, Mis-modeled peptide (identified by red ball at carbonyl oxgen position) is flagged by two successive CaBLAM outliers (magenta dihedrals), a bad clash (hot-pink spikes), and a bond-angle outlier (not shown), but no Ramachandran outlier. b, Correctly modeled peptide, involving a near-180° flip of the central peptide to achieve regular α-helical conformation. Ser 38 of T1/APOF model 60_1 is shown in (a); model 35_1 shown in (b). This example illustrates the most easily correctable situations: (1) for a CaBLAM outlier inside helix or β-sheet, regularize the secondary structure; (2) for two successive CaBLAM outliers, try flipping the central peptide. Molecular graphics were generated using KiNG. Note that sidechains are truncated by graphics clipping.
Extended Data Fig. 3 Evaluation of a short sequence misalignment within a helix.
Local Fit-to-Map and Coordinates-only scores are compared for a 3-residue sequence misalignment inside an ɑ-helix in an ab initio model submitted to the Challenge (APOF 2.3 Å 54_1). a, Model residues 14–42 vs target map (blue: correctly placed residues, yellow: mis-threaded residues 25–29, black: APOF reference model, 3ajo). b, Structure-based sequence alignment of the ab initio model (top) vs. reference model (bottom). c, Local Fit-to-Map scores (screenshot from Challenge model evaluation website Fit-to-Map Local Accuracy tool). Curves are shown for Phenix Box_CC (orange), EMDB Atom Inclusion (purple), Q-score (red) EMRinger (green), and SMOC (blue). The score values for model residue Leu 28 are shown in the box at right. d, Residue scores were calculated using the Molprobity server. The mis-threaded region is boxed in (b-d). Panels (a) and (b) were generated using UCSF Chimera.
Extended Data Fig. 4 Modeling errors around omitted Zinc ligand in ADH.
Target 4 (ADH) density map with examples of modeling errors caused by omission of Zinc ligand. a, Reference structure with Zinc metal ion (gray ball) coordinated by 4 Cysteine residues (blue sidechains). b-e, Submitted models missing Zinc (labels indicate the group_model ids). All have geometry and/or conformational violations as flagged by MolProbity CaBLAM (magenta pseudobonds), cis-nonPro (green parallelograms), Ramachandran (green pseudobonds), Cbeta (magenta spheres), and angle (blue and red fans). Model (b) has backbone conformation very close to correct, while (b) and (c) both have flags indicating bad geometry of incorrect disulfide bonds. Models (c) and (d) have backbone distortions, and (e) is mistraced through the Zn density. Molecular graphics were generated using KiNG.
Extended Data Fig. 5 Fit-to-Map Scores with and without refined B-factors (ADP).
Two representative metrics are shown: a, CCmask correlation, b, FSC05 resolution−1. Each plotted point indicates the calculated score for atom positions with B-factors included (horizontal axis) versus the calculated score for atom positions alone (vertical axis). Plot symbols identify map targets. Of 63 models total, 33 included refined B-factors. Differing scores +/- B-factors contribute off-diagonal points (black dotted lines are reference diagonals).
Extended Data Fig. 6 Group performance evaluations.
a, Group composite Z-scores plotted by metric category. The nine teams with highest Coordinate-only composite Z-score rankings are shown, sorted left to right. The plot illustrates that by group/method, Coordinate-only scores are poorly corelated with Fit-to-Map and Comparison-to-Reference scores. In contrast, a modest correlation is observed between Fit-to-Map and Comparison-to-Reference scores. b, Averaged model composite Z-scores plotted for ab initio modeling groups at higher resolution (T1 at 1.8 Å, T2 at 2.3 Å) and lower resolution (T3 at 3.1 Å, T4 at 2.9 Å). In each case 6 groups produced very good models (Z ≥ 0.3; green pins), though not the same set. Runner-up clusters (−0.3 ≤ Z < 0.3) are shown with gold pins. Individual scores and order shift with alternate choices of evaluation metrics and weights, but the clusters at each resolution level are stable. Composite Z-scores were calculated as described in Methods.
Supplementary information
Supplementary Information
Supplementary Fig. 1.
Source data
Source Data Fig. 1
Spreadsheet and graph, EM entries in PDB.
Source Data Fig. 4
Spreadsheets and graphs, 2019 Model Metric Challenge results.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lawson, C.L., Kryshtafovych, A., Adams, P.D. et al. Cryo-EM model validation recommendations based on outcomes of the 2019 EMDataResource challenge. Nat Methods 18, 156–164 (2021). https://doi.org/10.1038/s41592-020-01051-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41592-020-01051-w
This article is cited by
-
Accurate Prediction of Protein Structural Flexibility by Deep Learning Integrating Intricate Atomic Structures and Cryo-EM Density Information
Nature Communications (2024)
-
Cryo-EM structure and B-factor refinement with ensemble representation
Nature Communications (2024)
-
Bayesian reweighting of biomolecular structural ensembles using heterogeneous cryo-EM maps with the cryoENsemble method
Scientific Reports (2024)
-
Outcomes of the EMDataResource cryo-EM Ligand Modeling Challenge
Nature Methods (2024)
-
Improvement of cryo-EM maps by simultaneous local and non-local deep learning
Nature Communications (2023)