Abstract
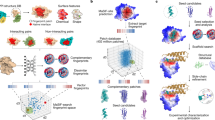
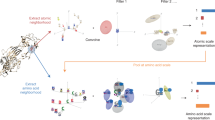
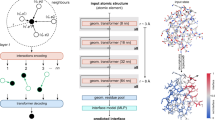
Predicting interactions between proteins and other biomolecules solely based on structure remains a challenge in biology. A high-level representation of protein structure, the molecular surface, displays patterns of chemical and geometric features that fingerprint a protein’s modes of interactions with other biomolecules. We hypothesize that proteins participating in similar interactions may share common fingerprints, independent of their evolutionary history. Fingerprints may be difficult to grasp by visual analysis but could be learned from large-scale datasets. We present MaSIF (molecular surface interaction fingerprinting), a conceptual framework based on a geometric deep learning method to capture fingerprints that are important for specific biomolecular interactions. We showcase MaSIF with three prediction challenges: protein pocket-ligand prediction, protein–protein interaction site prediction and ultrafast scanning of protein surfaces for prediction of protein–protein complexes. We anticipate that our conceptual framework will lead to improvements in our understanding of protein function and design.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The bound PDBs in the training/testing set and the computed surfaces with chemical features are available at Zenodo with https://doi.org/10.5281/zenodo.2625420. The unbound PDBs in the test set are provided in the github repository. All scripts to generate the datasets are available at https://github.com/lpdi-epfl/masif.
Code availability
All code was implemented in Python and MATLAB. Neural networks were implemented using TensorFlow65. Both the code and scripts to reproduce the experiments of this paper are available at https://github.com/lpdi-epfl/masif66. The github repository also provides a PyMOL67 plugin for the visualization of feature-rich molecular surfaces, used for the figures in this paper. All source code is provided under an Apache 2.0 permissive free software license.
References
Donald, B. R. Algorithms in Structural Molecular Biology (MIT Press, 2011).
Zhang, Q. C. et al. Structure-based prediction of protein–protein interactions on a genome-wide scale. Nature 490, 556–560 (2012).
Hermann, J. C. et al. Structure-based activity prediction for an enzyme of unknown function. Nature 448, 775–779 (2007).
Kortemme, T. et al. Computational redesign of protein–protein interaction specificity. Nat. Struct. Mol. Biol. 11, 371–379 (2004).
Yang, J. et al. The I-TASSER Suite: Protein Structure and Function Prediction. Nat. Methods 12, 7–8 (2015).
Planas-Iglesias, J. et al. Understanding protein–protein interactions using local structural features. J. Mol. Biol. 425, 1210–1224 (2013).
Cong, Q., Anishchenko, I., Ovchinnikov, S. & Baker, D. Protein interaction networks revealed by proteome coevolution. Science 365, 185–189 (2019).
Richards, F. M. Areas, volumes, packing, and protein structure. Annu. Rev. Biophysics Bioeng. 6, 151–176 (2003).
Bronstein, M.M., Bruna, J., Lecun, Y., Szlam, A. & Vandergheynst, P. Geometric Deep Learning: Going Beyond Euclidean Data. IEEE Signal Processing Magazine 34, https://doi.org/10.1109/MSP.2017.2693418 (2017).
Shulman-Peleg, A., Nussinov, R. & Wolfson, H. J. Recognition of functional sites in protein structures. J. Mol. Biol. 339, 607–633 (2004).
Duhovny, D., Nussinov, R. & Wolfson, H.J. Efficient unbound docking of Rigid molecules. in Proc. International Workshop on Algorithms in Bioinformatics (eds., Guigó, R. and Gusfield, D.) 2452, 185–200 (Springer, 2002); https://doi.org/10.1007/3-540-45784-4_14
Sharp, K. Electrostatic interactions in macromolecules: theory and applications. Annu. Rev. Biophys. Biomol. Struct. 19, 301–332 (1990).
Daberdaku, S. & Ferrari, C. Antibody interface prediction with 3D Zernike descriptors and SVM. Bioinformatics 35, 1870–1876 (2019).
Kihara, D., Sael, L., Chikhi, R. & Esquivel-Rodriguez, J. Molecular surface representation using 3D Zernike descriptors for protein shape comparison and docking. Curr. Protein Pept. Sci. 12, 520–530 (2011).
Zhu, X., Xiong, Y. & Kihara, D. Large-scale binding ligand prediction by improved patch-based method Patch-Surfer2.0. Bioinformatics 31, 707–713 (2015).
Venkatraman, V., Yang, Y. D., Sael, L. & Kihara, D. Protein–protein docking using region-based 3D Zernike descriptors. BMC Bioinformatics 10, 407 (2009).
Yin, S., Proctor, E. A., Lugovskoy, A. A. & Dokholyan, N. V. Fast screening of protein surfaces using geometric invariant fingerprints. Proc. Natl Acad. Sci. USA 106, 16622–16626 (2009).
Krizhevsky, A., Sutskever, I. & Hinton, G. Imagenet classification with deep convolutional neural networks. in Advances in Neural Information Processing Systems 1097–1105 (eds., F. Pereira, C.J.C. Burges, L. Bottou and K.Q. Weinberger) Curran Associates, Inc. (2012).
Monti, F. et al. Geometric deep learning on graphs and manifolds using mixture model CNNs. in Proc. 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017 5425–5434 (eds., R. Chellappa, Z. Zhang, and A. Hoogs) (2017).
Masci, J., Boscaini, D., Bronstein, M. M. & Vandergheynst, P. Geodesic convolutional neural networks on Riemannian manifolds. In Proc. IEEE International Conference on Computer Vision 832–840 (eds., R. Bajcsy, G. Hager, and Y. Ma) (2015).
Sanner, M. F., Olson, A. J. & Spehner, J. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers 38, 305–320 (1996).
Koenderink, J. J. & van Doorn, A. J. Surface shape and curvature scales. Image Vis. Comput. 10, 557–564 (1992).
Kyte, J. & Doolittle, R. F. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 157, 105–132 (1982).
Jurrus, E. et al. Improvements to the APBS biomolecular solvation software suite. Protein Sci. 27, 112–128 (2018).
Kortemme, T., Morozov, A. V. & Baker, D. An orientation-dependent hydrogen bonding potential improves prediction of specificity and structure for proteins and protein–protein complexes. J. Mol. Biol. 326, 1239–1259 (2003).
Chubukov, V., Gerosa, L., Kochanowski, K. & Sauer, U. Coordination of microbial metabolism. Nat. Rev. Microbiol. 12, 327–340 (2014).
Konc, J. et al. ProBiS-CHARMMing: web interface for prediction and optimization of ligands in protein binding sites. J. Chem. Inf. Modeling 55, 2308–2314 (2015).
Ritschel, T., Schirris, T. J. & Russel, F. G. KRIPO—a structure-based pharmacophores approach explains polypharmacological effects. J. Cheminform. 6(Suppl 1): O26. https://doi.org/10.1186/1758-2946-6-S1-O26 (2014).
Ehrt, C., Brinkjost, T. & Koch, O. A benchmark driven guide to binding site comparison: An exhaustive evaluation using tailor-made data sets(ProSPECCTs). PLoS Comput. Biol. 14(11), e1006483 (2018).
Ha, J. Y. et al. Crystal structure of d-erythronate-4-phosphate dehydrogenase complexed with NAD. J. Mol. Biol. 366, 1294–1304 (2007).
Gauss, G. H., Kleven, M. D., Sendamarai, A. K., Fleming, M. D. & Lawrence, C. M. The crystal structure of six-transmembrane epithelial antigen of the prostate 4 (Steap4), a ferri/cuprireductase, suggests a novel interdomain flavin-binding site. J. Biol. Chem. 288, 20668–20682 (2013).
Jones, S. & Thornton, J. M. Prediction of protein–protein interaction sites using patch analysis. J. Mol. Biol. 272, 133–143 (1997).
Porollo, A. & Meller, J. Prediction-based fingerprints of protein–protein interactions. Proteins 66, 630–645 (2007).
Northey, T. C., BarešiÄ, A. & Martin, A. C. R. IntPred: a structure-based predictor of protein–protein interaction sites. Bioinformatics 34, 223–229 (2018).
Xue, L. C., Dobbs, D., Bonvin, A. M. J. J. & Honavar, V. Computational prediction of protein interfaces: a review of data driven methods. FEBS Lett. 589, 3516–3526 (2015).
Murakami, Y. & Mizuguchi, K. Applying the naïve Bayes classifier with kernel density estimation to the prediction of protein–protein interaction sites. Bioinformatics 26, 1841–1848 (2010).
Fleishman, S. J. et al. Computational design of proteins targeting the conserved stem region of influenza hemagglutinin. Science 332, 816–821 (2011).
King, N. P. et al. Computational design of self-assembling protein nanomaterials with atomic level accuracy. Science 336, 1171–1174 (2012).
Correia, B. E. et al. Proof of principle for epitope-focused vaccine design. Nature 507, 201–206 (2014).
Muja, M. & Lowe, D. G. Scalable nearest neighbor algorithms for high dimensional data. IEEE Trans. Pattern Anal. Mach. Intell. 36, 2227–2240 (2014).
Greisen, P. J. et al. Computational design of environmental sensors for the potent opioid fentanyl. eLife 6, 1–23 (2017).
Chopra, S., Hadsell, R. & LeCun, Y. Learning a similarity metric discriminatively, with application to face verification. in Proc. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition 1, 539–546 (eds., M. Hebert and D. Kriegman) IEEE (2005).
Pierce, B. G., Hourai, Y. & Weng, Z. Accelerating protein docking in ZDOCK using an advanced 3D convolution library. PLoS ONE 6, e24657 (2011).
Lensink, M. F., Velankar, S. & Wodak, S. J. Modeling protein–protein and protein–peptide complexes: CAPRI 6th edition. Proteins 85, 359–377 (2017).
Pierce, B. & Weng, Z. A combination of rescoring and refinement significantly improves protein docking performance. Proteins 72, 270–279 (2008).
Zak, K. M. et al. Structure of the complex of human programmed death 1, PD-1, and its ligand PD-L1. Structure 23, 2341–2348 (2015).
Huang, P. S., Boyken, S. E. & Baker, D. The coming of age of de novo protein design. Nature 537, 320–327 (2016).
Hallen, M. A. et al. OSPREY 3.0: Open-source protein redesign for you, with powerful new features. J. Computational Chem. 39, 2494–2507 (2018).
Leaver-Fay, A. et al. in Methods in Enzymology (eds Johnson, M. J. & Brand, L.) 545–574 (Elsevier, 2010); https://doi.org/10.1016/b978-0-12-381270-4.00019-6
Word, J. M., Lovell, S. C., Richardson, J. S. & Richardson, D. C. Asparagine and glutamine: using hydrogen atom contacts in the choice of side-chain amide orientation. J. Mol. Biol. 285, 1735–1747 (1999).
Zhou, Q. PyMesh—Geometry Processing Library for Python. Software available for download at https://github.com/PyMesh/PyMesh (2019).
Dolinsky, T. J. et al. PDB2PQR: expanding and upgrading automated preparation of biomolecular structures for molecular simulations. Nucleic Acids Res. 35 (suppl. 2), W522–W525 (2007).
Baker, N. A., Sept, D., Joseph, S., Holst, M. J. & McCammon, J. A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl Acad. Sci. USA 98, 10037–10041 (2001).
O’Connell, A. A., Borg, I. & Groenen, P. Modern multidimensional scaling: theory and applications. J. Am. Stat. Assoc. 94, 338–339 (2006).
Bonet Martínez, J. Exploiting Protein Fragments in Protein Modelling and Function Prediction (Univ. Pompeu Fabra, 2015).
Baspinar, A. et al. PRISM: a web server and repository for prediction of protein–protein interactions and modeling their 3D complexes. Nucleic Acids Res. 42, W285–W289 (2014).
Liu, Z. et al. PDB-wide collection of binding data: current status of the PDBbind database. Bioinformatics 31, 405–412 (2015).
Dunbar, J. et al. SAbDab: the structural antibody database. Nucleic Acids Res. 42, D1140–D1146 (2013).
Vreven, T. et al. Updates to the integrated protein–protein interaction benchmarks: docking Benchmark version 5 and Affinity Benchmark version 2. J. Mol. Biol. 427, 3031–3041 (2015).
Fu, L., Niu, B., Zhu, Z., Wu, S. & Li, W. CD-HIT: accelerated for clustering the next-generation sequencing data. Bioinformatics 28, 3150–3152 (2012).
Zhang, Y. & Skolnick, J. TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. 33, 2302–2309 (2005).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Presented at International Conference on Learning Representations (ICLR) https://arxiv.org/abs/1412.6980 (2015).
Svoboda, J., Masci, J. & Bronstein, M. M. Palmprint recognition via discriminative index learning. In Proc. International Conference on Pattern Recognition 4232–4237 (eds. P. Gomez, S. Velastin) (2017); https://doi.org/10.1109/ICPR.2016.7900298
Zhou, Q.-Y., Park, J. & Koltun, V. Open3D: a modern library for 3D data processing. Technical report, available at: https://arxiv.org/abs/1801.09847 (2018).
Abadi, M. et al. TensorFlow: a system for large-scale machine learning. in 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16) 265–283 (eds., K. Keeton, T. Roscoe) (2016).
Pablo Gainza & Freyr S. LPDI-EPFL/masif: MaSIF Paper Software Release (Zenodo, 2019); https://doi.org/10.5281/zenodo.3519996
The PyMOL Molecular Graphics System v.1.8 (Schrödinger LLC, 2015).
Acknowledgements
We thank J. Bonet for helpful comments and J. Bonet, S.S. Vollers, P. de los Rios, S. Fleishman and A. Baptista for critical feedback on the manuscript. This work was funded by generous grants from the European Research Council (Starting grant no. 716058 to B.E.C. and Consolidator grant no. 724228 to M.M.B.). B.E.C. is also supported by the Swiss National Science Foundation (grants 31003A_163139 and 310030_188744) and the Biltema Foundation. P.G. is sponsored by an EPFL-Fellows grant funded by an H2020 Marie Sklodowska-Curie action and by the NCCR in Molecular Systems Engineering. F.S. is supported by a PhD fellowship from the Swiss Data Science Center. M.B. is partially supported by the Royal Academy Wolfson Research Merit Award, Google Faculty Research Awards. MaSIF’s computations have been performed using the facilities of the Scientific IT and Application Support Center of EPFL.
Author information
Authors and Affiliations
Contributions
P.G., F.S., F.M., M.M.B. and B.E.C designed the overall method and approach. M.M.B. and B.E.C supervised the research. P.G., F.M. and F.S. developed the base MaSIF method. P.G. designed and implemented MaSIF-site and MaSIF-search. F.S. designed and implemented MaSIF-ligand. F.S. and P.G. developed MaSIF-search’s second-stage alignment algorithm. F.S. and P.G. developed the second-stage scoring neural network. P.G., F.S., M.M.B. and B.E.C. analyzed the data. E.R. and D.B. assisted in the design and development of these methods. P.G., F.S., M.M.B. and B.E.C wrote the manuscript. All authors read and commented the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Arunima Singh and Allison Doerr were the primary editors on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Integrated supplementary information
Supplementary Figure 1 Example-based illustration on the importance of geodesic distances in modeling protein surfaces.
This example shows Trypsin (blue/red surface) in complex with the (cyan cartoon+line representation) (PDB ID 1PPE). We selected a point in the deep pocket of the interface, and colored in red every surface point within a 12 Å Euclidean radius-defined patch (left) or a 12 Å Geodesic radius-defined patch (right). The Euclidean patch (left, below) includes points on a different face of the protein, far from the binding site, while the geodesic patch only includes points in the face that interacts with the protein. This example shows that, especially in highly irregular surfaces the geodesic distances between points can be much larger than the Euclidean distances and that in such cases geodesic distances can be more relevant.
Supplementary Figure 2 Analysis of MaSIF-ligand performance for specific cofactors.
a. Confusion matrix of ligand specificity on a MaSIF-ligand neural network trained with all features. Number of pockets in each category: ADP:146, CoA:46, FAD:71, HEME:68, NAD:49, NADP:28, SAM:43. b. Subset of the confusion matrices showing the importance of the features in distinguishing pockets between highly similar ligands. Number of pockets in each category: ADP:146, NAD:49, NADP:28, SAM:43. c. Analysis of MaSIF-ligand’s discrimination between NADP and NAD on two specific examples: a bacterial oxidoreductase and a human dehydrogenase. The bacterial dehydrogenase in the test set binds to NAD (PDB ID 2O4C), while its closest structural homologue in the training set corresponds to a mammalian oxidoreductase (PDB ID 2YJZ), which binds to NADP. Here we scored the pocket surface by a discrimination score, which scores each point in the protein surface by its weight in the neural network’s distinction between NADP and NAD. Surface regions with high importance are shown in red, while those of low importance are shown in blue.
Supplementary Figure 3 MaSIF-site interface prediction score distribution for true positives (red) vs. true negatives (blue).
a. One convolutional layer obtains a ROC AUC value of 0.77 (n = 2192870 points from the test set) and b. Three convolutional layers obtain a ROC AUC value of 0.86 (n = 2192870 points from the test set).
Supplementary Figure 4 Comparison between MaSIF-site and two other predictors on a set of transient interactions.
a. ROC AUC values over all surface points of MaSIF-site vs. SPPIDER vs. PSIVER on 53 proteins involved in transient interactions. b. Histogram showing the distribution of ROC AUCs per protein for the 53 proteins on a residue basis for MaSIF-site, SPPIDER and PSIVER. c. Randomly-selected examples from the testing set comparing MaSIF-site prediction with SPPIDER.
Supplementary Figure 5 Performance of MaSIF-search fingerprints under different shape complementarity filters for the interacting patches, and effect of inverting input features.
a. We set up three classes of interacting patches, filtered by shape complementarity, and trained neural networks with each set. The sets are illustrated here with three examples, where the surface is colored according to shape complementarity from white (0.0) to red (1.0). b. Descriptor distance distribution plot for interacting and non-interacting patches depending on the shape complementarity class. c. ROC AUC values for the GIF descriptors, MaSIF descriptors trained only on geometry, chemistry, or both, and patches found in unbound proteins within each complementarity class (G+C ub). # of pairs of patches: high comp, 38038 positives and 38038 negatives; low comp.: 16798 positives and 16798 negatives; low comp. 21297 positive and 21297 negatives. d, e. MaSIF-search benefits from the inversion of features in the input. d. ROC AUCs of a network trained/tested with inversion (green) vs. a network trained/tested without inversion (blue) using both Geometric (G) and chemical (C) features. The plot’s ROC curve was computed on 13338 positive and 13338 negative pairs of samples. e. Performance of a network where electrostatics and the hbond features were inverted (green) vs. one in which they were not (blue), on a network trained with only chemical features.
Supplementary Figure 6 MaSIF-search protocol for the generation of protein complexes.
a. A fingerprint is computed on a selected target site (left). A database of proteins with precomputed fingerprints is searched for the K-most similar fingerprints. Once these are matched, a set of correspondences between the matched patches is found with the RANSAC algorithm, which uses the fingerprints of other points in the patch to obtain a good alignment. RANSAC selects the alignment with the most points within 1.5 Å of each other. The transformation is then scored using: Euclidean distances; fingerprint distances; and the normal products between neighboring points (see Methods). b. Neural network architecture for the alignment scoring function. Correspondences are first assigned between the aligned binder and target patches based on the nearest point in 3D space. For every correspondence, the 3D distance between the points, the Euclidean distance between the fingerprint descriptors and the product of their normals is input into the neural network. The input is a matrix of size 200 by 3: the maximum number of points allowed in the patch times the three features. The output is a 2-dimensional logit with the predicted score.
Supplementary Figure 7 Hybrid MaSIF-search/MaSIF-site protocol to identify true binders against PD-L1.
The target site is first predicted using MaSIF-site. Then a database of nearly 11,000 proteins is scanned, all patches with a MaSIF-site score > 0.9 and with a descriptor distance less than 1.7 are selected for alignments. Top candidates are matched using RANSAC, and reranked using the descriptor distance of all aligned points (described in Methods). The top predicted complex was the PD-L1:Mouse PD1 (PDB ID 3BIK), ranked #1 with an RMSD of 0.6 Å (shown here in pale orange). The PD-L1:Human PD1 (PDB ID 4ZQK), was ranked #8 with an RMSD of 0.3 Å. Both are shown overlaid over the initial complex (PDB ID 4ZQK). The entire runtime protocol took approximately 26 minutes (excluding descriptor precomputation time).
Supplementary Figure 8 The performance of MaSIF-search and MaSIF-site is not affected by a stricter structural split.
MaSIF-site and MaSIF-search’s test sets were split from the training sets using a hierarchical clustering approach based on a matrix of TM-scores. In the case of MaSIF-search this split was performed using the interface TM-score. (hierarchical split only, a, b, top left). Some structures in the test set still maintain a TM-score above 0.5 to at least one member in the training set. (a,b, top right) We performed a stricter split by eliminating all members of the test set whose maximum TM-score to any member of the training set was above 0.5. (a,b, bottom right). The stricter split did not affect performance. a. MaSIF-site (left) Hierarchical split only test set consists of 359 proteins decomposed into 2191879 patches. (right) Hierarchical split+strict test set consists of 169 proteins decomposed into 1042951 patches. b. MaSIF-search (left) Hierarchical split only test set consists of a total of 957 proteins decomposed into 13338 interacting patch pairs and same number of non-interacting pairs. (right) Hierarchical split+strict consists of 635 proteins decomposed into 7135 interacting patch pairs and same number of non-interacting pairs.
Supplementary Figure 9 Network architecture for MaSIF-ligand.
32 randomly sampled pocket patches are fed through convolutional layers followed by a fully connected layer (FC80). Descriptors are combined in a 80x80 covariance matrix followed by two fully connected layers (FC64 and FC7) and then softmax cross-entropy loss.
Supplementary Figure 10 Network architecture for MaSIF-site.
Patches are fed through convolutional layers followed by a series of fully connected layers (FC5, FC4, FC2), and finally a sigmoid cross-entropy loss.
Supplementary Figure 11 Network architecture for MaSIF-search.
Patches from the target and the corresponding binder or a random patch are fed through convolutional layers, followed by a fully connected layer (FC80). The L2-distance between the resulting descriptors is computed and the neural network is optimized to minimize this distance with respect to binder and maximize it with respect to the random patch.
Supplementary Figure 12 Total computation time for MaSIF-search and MaSIF-site for proteins of various sizes.
Proteins chains, of sizes: 50, 75, 100, 125, 200, 300, 500, were selected from the PDB. Each chain was run through both the MaSIF-site and MaSIF-search protocols, entailing: downloading the PDB, computing surfaces, input features, and coordinates, decomposing into patches, and computing MaSIF-site predictions and MaSIF-search descriptors. The y-axis shows the CPU user + System time + GPU time in minutes. GPU time consists of the time where the data is processed by the neural network, and was measured in real clock time (i.e. not GPU processor time). The total GPU time is low compared to the overall time, from 4 seconds for a 50-residue protein, to 12 seconds for a 500-residue protein. The line represents the regression fit to the n=7 data points and the shaded area represents the 95% confidence interval.
Supplementary information
Supplementary Information
Supplementary Figs. 1–12 and Notes 1–10.
Rights and permissions
About this article
Cite this article
Gainza, P., Sverrisson, F., Monti, F. et al. Deciphering interaction fingerprints from protein molecular surfaces using geometric deep learning. Nat Methods 17, 184–192 (2020). https://doi.org/10.1038/s41592-019-0666-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41592-019-0666-6
This article is cited by
-
PLAS-20k: Extended Dataset of Protein-Ligand Affinities from MD Simulations for Machine Learning Applications
Scientific Data (2024)
-
Inferring molecular inhibition potency with AlphaFold predicted structures
Scientific Reports (2024)
-
Opportunities and challenges in design and optimization of protein function
Nature Reviews Molecular Cell Biology (2024)
-
Sparks of function by de novo protein design
Nature Biotechnology (2024)
-
Programmable RNA base editing with photoactivatable CRISPR-Cas13
Nature Communications (2024)