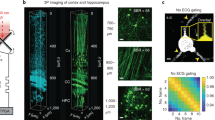
Abstract
Two-photon microscopy is a mainstay technique for imaging in scattering media and normally provides frame-acquisition rates of ~10–30 Hz. To track high-speed phenomena, we created a two-photon microscope with 400 illumination beams that collectively sample 95,000–211,000 µm2 areas at rates up to 1 kHz. Using this microscope, we visualized microcirculatory flow, fast venous constrictions and neuronal Ca2+ spiking with millisecond-scale timing resolution in the brains of awake mice.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The experimental data used for the analyses is available from the corresponding author upon reasonable request.
Code availability
The software code used for the analyses is available from the corresponding author upon reasonable request.
References
Kim, K. H., Buehler, C. & So, P. T. Appl Opt. 38, 6004–6009 (1999).
Kong, L. et al. Nat. Methods 12, 759–762 (2015).
Katona, G. et al. Nat. Methods 9, 201–208 (2012).
Prevedel, R. et al. Nat. Methods 13, 1021–1028 (2016).
Grewe, B. F., Langer, D., Kasper, H., Kampa, B. M. & Helmchen, F. Nat. Methods 7, 399–405 (2010).
Brakenhoff, G. J. et al. J. Microsc. 181, 253–259 (1996).
Cheng, L. C. et al. Opt. Express 20, 8939–8948 (2012).
Andresen, V., Egner, A. & Hell, S. W. Opt. Lett. 26, 75–77 (2001).
Fittinghoff, D. N., Wiseman, P. W. & Squier, J. A. Opt. Exp. 7, 273–279 (2000).
Bahlmann, K. et al. Opt. Exp. 15, 10991–10998 (2007).
Kleinfeld, D., Mitra, P. P., Helmchen, F. & Denk, W. Proc. Natl Acad. Sci. USA 95, 15741–15746 (1998).
Vignes, J.-R., Dagain, A., Guérin, J. & Liguoro, D. J. Neurosurg. 107, 1205–1210 (2007).
Wilt, B. A., Fitzgerald, J. E. & Schnitzer, M. J. Biophysical J. 104, 51–62 (2013).
Ghosh, K. K. et al. Nat. Methods 8, 871–878 (2011).
Komiyama, T. et al. Nature 464, 1182–1186 (2010).
Holekamp, T. F., Turaga, D. & Holy, T. E. Neuron 57, 661–672 (2008).
Feng, G. et al. Neuron 28, 41–51 (2000).
Inoue, M. et al. Nat. Methods 12, 64–70 (2015).
Kawashima, T. et al. Nat. Methods 10, 889–895 (2013).
Chen, T.-W. et al. Nature 499, 295–300 (2013).
Kim, T. H. et al. Cell Rep. 17, 3385–3394 (2016).
Podgorski, K. & Ranganathan, G. J. Neurophysiol. 116, 1012–1023 (2016).
Kalmbach, A. S. & Waters, J. J. Neurophysiol. 108, 3138–3146 (2012).
Picot, A. et al. Cell Rep. 24, 1243–1253 e1245 (2018).
Flusberg, B. A. et al. Nat. Methods 5, 935–938 (2008).
Gonzalez, R. C. & Woods, R. E. Digital Image Processing. (Prentice Hall, 2008).
Mukamel, E. A., Nimmerjahn, A. & Schnitzer, M. J. Neuron 63, 747–760 (2009).
Egner, A. & Hell, S. W. J. Opt. Soc. Am. A. 17, 1192–1201 (2000).
Acknowledgements
We thank Y.-S. Chen, E. Cocker, A. Fritz, K. Ghosh, B. Grewe, E.T. Ho, J.C. Jung, H. Kim, J. Lecoq, J. Li, J. Lu, J. Marshall, O. Rumyantsev, G. Sanchez, J. Savall, S. Sinha, T. Tasci, D. Vucinic, B. Wilt, G. Yin and B. Zhang for conversations and assistance, and K. Merkle for machining. M.J.S. received funds from the P.G. Allen Family Foundation, NSF Neuronex grant no. 1707261, and the HHMI. H.B. was funded by JST-CREST, AMED-Brain/MINDS and KAKENHI research grant nos. 16K13105, 17K19442 and 17H06312.
Author information
Authors and Affiliations
Contributions
T.Z. designed the microscope. T.Z., O.H. and R.C built the microscope. T.Z., O.H., R.C., Y.Z., M.J.W., C.W., J.Z.L., Y.G. and A.S. did imaging studies. O.H. and Y.Z. studied brain temperature. A.S. and O.H. performed patch-clamp studies. R.C. studied fluorescence scattering. T.Z., O.H., R.C., A.S. and B.A. analyzed data. M.I. and H.B. provided R-CaMP2. H.Z. provided transgenic mice. T.Z., O.H., A.S., R.C. and M.J.S. wrote the paper. M.J.S. supervised the project.
Corresponding author
Ethics declarations
Competing interests
T.Z. and M.J.S. patented the microscope. M.I. and H.B. filed a patent on R-CaMP2.
Additional information
Peer review information Nina Vogt was the primary editor on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Integrated supplementary information
Supplementary Figure 1 Mechanical layout of the microscope.
Computer-assisted design drawing of the microscope. Scale bar: 10 cm.
Supplementary Figure 2 Synchronized control signals for the high-speed microscope.
Schematics of the timing signals used to synchronize laser pulse emission, camera frame acquisition, the scanning cycle of the galvanometer mirror, and shuttering of the laser beam by the optical chopper, using the laser pulses as the seed clock. (a) A transistor-transistor logic (TTL) digital output from the laser has the same cycle frequency, f, as the laser repetition rate. Laser pulse emission is synchronized with the galvanometer mirror’s scanning cycle such that the scanning cycle duration, t1, contains an integral, uniform number of laser pulses (e.g. f · t1 is an integer). (b, c) Frame acquisition by the camera is triggered on the rising edge of a digital signal, b, and is synchronized with the triangular waveform of period t1 used to drive the galvanometer scanning mirror, c. The period, t1, was 2–10 ms for the biological images shown in this paper. Frame acquisition and the scanning cycle are both synchronized with laser pulse emission. For a subset of experiments (Fig. 2f–h) we acquired images at 1 kHz, by driving the scanning mirror at 500 Hz and recording separate images on the forward and backward phases of the scanning motion. (d) Mechanical movement of the scanning mirror follows the triangular command waveform with a slight temporal delay, Δt ~ 250 μs. Blue portions of the trace denote intervals during which the laser beam passes through the optical chopper (see Fig. 1a). Yellow portions denote intervals when the chopper blocks the beam. The beam passes through the chopper when the mirror is in the innermost 90% of its scanning range (marked as d1 on the graph).(e) The optical chopper shutters the laser beam during the turnaround portion of the scanning mirror’s motion. The duration, t2, during which the beam is blocked at each extremity of the scanning motion yields a duty cycle of 80% for the illumination of the specimen. (f) Block diagram showing the flow of synchronization signals.
Supplementary Figure 3 Basic characterizations of the microscope’s optical performance.
(a) Double-logarithmic plot of the fluorescence emission intensity as a function of the laser illumination intensity at the specimen plane, as determined with the laser beamlets focused and held stationary on the surface of a red fluorescent microscope slide. x-axis values denote the total laser illumination power delivered to the specimen across all 20 × 20 laser beamlets. y-axis values denote the mean fluorescence intensity across a square region of interest containing 10,000 pixels. The green line is a parametric fit to the data using the equation log(y) = A log(x) + B, where A and B are the fitting parameters. The slope, A (2.02 ± 0.06; 95% confidence interval), is an indicator of the quadratic relationship between the fluorescence emission and laser illumination intensities. (b) The microscope’s lateral optical point-spread function, as determined by focusing the laser beamlets on the surface of a red fluorescent slide, using the sCMOS camera to acquire fluorescence images of the entire set of stationary foci, and analyzing the individual images from five different foci (one at the center of the field of view and four at peripheral edges of the image). Colored data points: Cross-sectional fluorescence intensity profiles of each image (one color for each of the five selected laser foci). FWHM lateral resolution: 1.4 ± 0.1 μm (mean ± s.d; N = 5 beamlet foci), as determined from Gaussian fits to the five cross-sectional profiles. Blue curve: A Gaussian fit (for display purposes only) to the aggregated dataset created by combining the data from the five different laser foci.
Supplementary Figure 4 Verification of safe power levels by in vitro whole-cell patch clamp recordings and trans-membrane impedance measurements in parvalbumin-positive cortical interneurons expressing tdTomato.
(a) Traces of electrical activity acquired in the same neuron using +50 pA of injected current, after imaging sessions of 0, 15 and 30 min. Traces are representative of data from 4 different cells, each studied for a 30-min-duration comprising alternating 30-s-periods of imaging (1.1 mW per beamlet; 200 kHz laser emission rate) and 2-min-periods of recovery, during which we iterated through different levels of injected current (–200 pA to +50 pA in steps of 50 pA; constant current for 1 s at each level before progressing to the next). (b) Temporal widths (FWHM) of action potential waveforms for the 4 different cells over 30 min (N = 313 spikes in total). (c) Trans-membrane impedance values (N = 4 cells) across 30 min. Error bars: s.d.
Supplementary Figure 5 Estimation of action potential initiation times to within ±12 ms (s.d.). via 1-kHz-two-photon Ca2+ imaging.
(a) Trans-membrane potentials of individual cortical pyramidal cells monitored in live brain tissue slices via whole-cell patch clamp electrophysiological recording (black trace; 1–5 spikes evoked with 2-ms-long current pulses of 0.5–1.7 nA at a rate of 150 Hz) during simultaneous monitoring of the cell’s somatic Ca2+ dynamics (red trace) with 1-kHz-two-photon imaging (100 kHz laser repetition rate; 0.7 mW per beamlet at the specimen) and the fluorescent Ca2+ indicator Calbryte-590. Data in panels a–i were acquired in 8 cells in neocortical slices from 3 mice. (b) Red trace: Mean Ca2+ transient time course, computed as the mean Ca2+ transient waveform (ΔF(t)/F0) evoked in response to 80 isolated spikes or 150-Hz bursts of spikes, averaged over 8 cells (10 traces per cell). Purple trace: A parametric fit of the form \(f\left( t \right) = \frac{{Ae^{ - (t - t_0)/\tau _1}}}{{1 + e^{ - (t - t_0)/\tau _2}}}\), used in panels c–i as a matched filter for the estimation of spike or spike burst initiation times, where A, t0, τ1, τ2, are, respectively, the waveform’s amplitude, time of half-rise, decay-time constant and logistic-growth-rate constant (Methods). Fit parameter values: A = 12 ± 1.2%, t0 = 11 ± 2.0 ms, τ1 = 766 ± 80 ms, and τ2 = 5.6 ± 1.9 ms. (c) Black traces: Whole-cell patch clamp electrophysiological recordings of neuronal trans-membrane potentials, illustrating one, three or five spikes. Red traces: Simultaneously recorded somatic Ca2+ activity traces (ΔF(t)/F0). A purple dot marks the estimated occurrence time of each spike or spike burst, determined as the time bin at which application of the matched filter, determined as in panel b, yielded its maximum output value. (d–f) Trials with individual spikes, d, bursts of 3 spikes evoked at 150 Hz, e, or bursts of 3 spikes evoked at 10 Hz, f. Dotted vertical lines indicate the spike or spike burst times obtained from the electrophysiological recordings (black traces). Purple dots indicate the occurrence times estimated from the Ca2+ transient waveforms (red traces) by using the matched filter. (g) Histogram of timing errors, computed as the difference between the estimated spike or spike burst initiation times as determined using an unbiased estimator and the corresponding times directly observed in the electrophysiological recordings. RMS timing estimation error was 11.6 ms, aggregated across individual spikes and spike bursts. (h) Histogram of timing errors for spike bursts. Unlike in panel g, the timing errors plotted in h and i include the systematic mean biases in timing estimation. For spike bursts, the estimation bias was –0.3 ms, and the s.d. around the bias was 11.7 ms. (i) Histogram of timing errors for individual spikes, revealing a systematic mean bias of –6.9 ms and a s.d of 10.1 ms. (j) Assessments of how fluorescence scattering might have affected the Ca2+ imaging data in our dual optical-electrical recordings, performed by quantifying how the fluorescence signals, ΔF(t)/F0, during a somatic Ca2+ transient declined as a function of the lateral displacement from the neural cell body. The graph shows example ΔF(t)/F0 traces determined within individual regions-of-interest (ROIs), which either match the cell body (black trace) or are 1.6-μm-diameter circles centered within different ranges away from the edge of the cell’s ROI (colored traces). Each empirical curve is shown together with a parametric fit of the same form, \(f\left( t \right) = \frac{{Ae^{ - (t - t_0)/\tau _1}}}{{1 + e^{ - (t - t_0)/\tau _2}}}\), used in panel b to characterize somatic Ca2+ transients. These examples are representative of the data from a total of 418 ROIs studied in the vicinity of 3 different cells. (k) Plots of the amplitudes of Ca2+ transient signals (mean ± s.d.) from the fit parameters, A, determined as in panel j for 1.6-μm-diameter-ROIs centered at different distances from the edge of the cell’s ROI. The values of the Ca2+ transient amplitudes are normalized to those observed at the cell body. Solid blue curve is a fit to the data (418 total ROIs in the vicinity of 3 different neurons) using a declining exponential function (length constant: 1.4 ± 0.2 μm). Dashed black curve is a theoretical prediction for the distance-dependent decline of fluorescence Ca2+ signals, computed by convolving the experimentally measured optical point spread function (Supplementary Fig. 8a) with the cell body ROI, performing the same analysis using 1.6-μm-diameter-ROIs as applied to the real data, and then fitting a declining exponential curve (length constant: 3.4 ± 0.06 μm) to the results. Ca2+ transient waveforms in c–f are shown after median-filtering (30 ms window) of the ΔF(t)/F0 traces. The ΔF(t)/F0 traces in j were median-filtered over a 100 ms window. Uncertainties to fit parameters in b and k are 95% confidence intervals.
Supplementary Figure 6 Computational simulations of how the Ca2+ transient timing estimation accuracy improves with increases in the imaging frame rate.
Results from simulations of Ca2+ activity under realistic experimental conditions. Ca2+ transients were parametrized by the product of a rising sigmoid function and a decaying exponential, with peak amplitudes of 100% ΔF/F and time constants of rise (0.2 s) and decay (1 s) similar to those attained with GCaMP6f (Fig. 3). Traces contained Poisson-distributed photon shot noise, with a variance equal to the mean number of photons per time bin. Each trace’s signal-to-noise ratio (SNR) was determined as the ratio of the mean photon flux to its standard deviation under baseline conditions (i.e. in the absence of a Ca2+ transient), sampled at 10 Hz. (a) Simulated Ca2+ transient waveforms at equivalent fluorescence emission levels, sampled at data acquisition rates of 10 Hz (brown trace), 100 Hz (red trace), and 1000 Hz (pink trace). (b) The color-corresponding Ca2+ transients in panel a, after median filtering (0.1 s time constant). Black traces are parametric fits to the waveform. (c) Histograms of spike timing estimation accuracy, as estimated based on parametric fits such as that shown in panel b, across 1000 different simulated Ca2+ transient events for each of the three data acquisitions rates (10 Hz, brown data; 100 Hz, red data; and 1000 Hz, pink data). (d) Plots showing how spike timing estimation accuracy improved with increases in data acquisition rate, for Ca2+ activity traces simulated across a range of different signal-to-noise (SNR) ratios. SNR values stated in the legend are for a 10 Hz image frame acquisition rate. Shading indicates s.d. over 1000 different simulated Ca2+ transient events.
Supplementary Figure 7 Maintenance of brain temperature within 2 °C of normal body temperature during high-speed two-photon imaging in awake mice.
Studies of the brain temperature variations that arose during high-speed two-photon imaging and imaging protocols that kept the brain in the range of normal body temperature.(a) Inset: An image showing a thermocouple implanted beneath a 4.5-mm-diameter glass window in the cranium of a GCaMP6f-tTA-dCre mouse, proximal to the site of two-photon imaging. Red dashed box encloses the field-of-view for high-speed two-photon imaging. Main panel: Measurements of peak brain temperature, determined via 10-Hz-sampling of brain temperature within 20-s-periods of two-photon imaging (400 beamlets; 2 mW illumination power per beamlet; 100 Hz image frame acquisition rate; 200 kHz laser repetition rate), plotted as a function of the lateral distance between the tip of the thermocouple (100-200 µm beneath the dura) and the center of the field-of-view. Peak temperature declined linearly with this distance and the beamlet power with a proportionality constant of –1.07 ± 0.03 °C · mm-1 · mW-1. Error bars denote s.d. across N = 4 bouts of imaging (each 20 s in duration) per data point. (b) Example traces of brain temperature measured with a thermocouple located within ~0.5 mm of the same field-of-view before, during and after 20-s-periods of two-photon imaging (gray shading) at one of six different illumination power levels (0.125–3 mW per beamlet; 400 beamlets; 100 Hz image frame acquisition rate; 200 kHz laser repetition rate). Due to the cranial window, in the absence of laser illumination the brain temperature was ≥10 °C below normal body temperature in mice, as previously reported23. The example traces are representative of data taken at 6 different fields-of-view studied in a total of 3 mice. (c) Time-course of the temperature measurements in panel b, normalized by illumination power. The blue trace and shading denote, respectively, the mean and s.d. of the same 6 time-courses shown in b, divided by total illumination power. Red trace: Parametric fits to the rising and declining phases of the temperature time course using two different exponential functions with distinct time constants (τ = 0.092 ± 0.001 s–1 and 0.071 ± 0.0002 s–1 for the rising and declining phases, respectively). Inset: Peak temperatures, attained at the end of each 20-s-period of illumination, plotted as a function of the laser beamlet power (linear proportionality constant: 5.5 ± 0.6 °C · mW-1). Each curve shows the data from one of 6 different fields-of-view, studied in a total of 3 mice. (d) Validation of three different imaging protocols to keep the brain within 2 °C of normal body temperature (37 ± 2 °C; shaded regions of the graphs). Solid traces are empirical measurements. Dotted lines are the predicted temperature values based on the kinetic parameters determined as in panel c. At 1 mW power per beamlet (400 beamlets in total), the illumination was continuous and the brain temperature reached ~39 °C after ~190 s of illumination. At 2 mW and 3 mW per beamlet, periods of imaging and rest were interleaved, mimicking the repetitive trial structure of a rodent behavioral task that might normally be performed in the context of a brain-imaging experiment. Uncertainty values stated here for all fit parameters are the 95% confidence intervals.
Supplementary Figure 8 Crosstalk due to fluorescence scattering between adjacent image tiles is ≲8% at imaging depths ≲500 μm in tissue.
Assessments of how fluorescence scattering impacts the spatial distribution of fluorescence signals emitted by a localized source in tissue. A stationary laser beam induced localized two-photon excited fluorescence at different depths in fixed coronal brain slices from GCaMP6f-tTA-dCre mice expressing GCaMP6f in layer 2/3 neocortical pyramidal cells. The resulting fluorescence images captured by the sCMOS camera (Fig. 1a) allowed evaluations of the spatial distributions of fluorescence intensity as a function of the lateral distance from the laser focus. Data in this figure are based on averages of these distributions over all polar angles and 50 different individual locations of the laser beam for each of 51 different depths in tissue and 7 different cortical regions. These mean spatial distributions of fluorescence yielded the probability density functions in panels a–c, PS (x, y), governing the lateral spatial distribution of detected fluorescence relative to a laser focal spot at x = y = 0, as well as the crosstalk probabilities in panel d, pi, j, that a fluorescence photon excited by one beamlet in the laser illumination array (Fig. 1a) would scatter in tissue to such an extent that it could be detected on the camera in an image tile associated with a nearby laser beamlet, i tiles away in the x-dimension and j tiles away in the y-dimension. (a) Plots of PS (x, y) for a laser beam positioned at the tissue surface (left) and 300 μm beneath the surface (right). The two square boxes within the right plot denote image tiles, each d = 24 μm wide, to the right of the laser focus for j = 0 and i = 1 and i = 2. Scale bars: 25 μm. (b) Left, Cross-sectional profiles of PS (x, y), i.e., the functions PS (x, 0), plotted for a range of different depths in tissue up to 500 μm beneath the tissue surface. Right, The same cross-sectional profiles but with each profile normalized such that PS (0, 0) = 1. (c) 4 example cross-sectional profiles, PS (x, 0), from panel b, illustrating how scattering affects the spatial distribution of fluorescence excited at 4 different depths in tissue. (d) Plots of the depth-dependent crosstalk probability (on a y-axis spanning 0-8%) that a fluorescence photon excited by one laser beamlet scatters to a nearby image tile corresponding to the location of either a nearest-neighbor, p0,1, or a next-nearest neighbor beamlet, p0,2, as computed from the measured PS (x, y) distributions for both a 15-µm-separation (top) and a 24-µm-separation (bottom) between adjacent laser foci in the specimen plane. Note that with the larger, 24-µm-separation spacing between adjacent beamlets, the greater area per image tile counteracts the greater separation between tiles, such that the crosstalk probabilities are comparable to those for a 15-µm-separation between adjacent beamlets. These determinations of pi, j informed subsequent image reconstructions based on sub-sampling (Supplementary Fig. 9). Shading denotes s.d. across n = 7 different locations in cortex. (e) Estimates of the depth-dependent decline in fluorescence Ca2+ signals that would occur in a neural Ca2+ imaging study, computed using the empirically determined PS (x, y) distributions for 50 different depths in neocortical tissue. For each depth in tissue, the corresponding PS (x, y) distribution was convolved with a uniform, circularly symmetric fluorescence source (12 µm in diameter) intended to model a neocortical neural cell body. Green curve shows the proportion of computed fluorescence signals remaining inside the cell body perimeter after this convolution. Black curve is a parametric fit to the signal decline as a function of the depth in tissue using a decaying exponential function, e−z/zS, with a characteristic decay length of zS = 142 ± 30 µm (s.d.). Green shading denotes s.d. across the measurements taken at n = 7 different locations in cortex.
Supplementary Figure 9 Computational image reconstructions using image sub-samples.
Assessments of the potential improvements in imaging depth attainable by operating the high-speed two-photon microscope in a sub-sampling mode, in which the camera acquires multiple image frames during each scanning cycle of the galvanometer, such that scattered fluorescence photons can be computationally re-assigned to their most likely positions of origin in the specimen by using the known positions of the laser foci for each acquired image frame. Due to the speed limitations of existing scientific-grade cameras, these assessments were low-speed, proof-of-concept studies using image sub-samples acquired at 256 Hz, as well as a 24-µm-separation between the foci of adjacent laser beamlets in the specimen plane, a 200-kHz laser repetition rate, and fixed brain slices with fluorescent neurons expressing either tdTomato, YFP or GCaMP6 (Methods). The power per beamlet delivered to the sample ranged from 0.2 mW for images acquired ~100 μm deep within tissue, to 1 mW for images acquired ~500 μm deep within tissue. (a) Schematic illustration of the standard process of image formation used elsewhere throughout the paper. As the grid of laser beamlets sweeps across the image plane, the sCMOS camera sums the fluorescence signals captured across an entire laser-scanning cycle. In principle, however, a camera operating at faster image acquisition rates could capture the distinct fluorescence emission patterns for different positions of the laser beamlet grid. Access to these patterns permits superior methods of image reconstruction that correct for fluorescence scattering, as illustrated in panels b–d. (b) Schematic illustration of Reconstruction Method 1, in which a blind deconvolution algorithm is applied to each image sub-sample, followed by a maximum projection operation across the entire set of image sub-samples, to attain the final reconstructed image (Methods). The kernel for the deconvolution approach is initialized using the Ps(x,y) functions determined in Supplementary Fig. 8a for the relevant fluorophore and depth in tissue. (c) Schematic illustration of Reconstruction Method 2, which incorporates the knowledge that the laser illumination pattern has the form of a square grid. The orientation of the grid is determined for each image sub-sample by using a Radon transform, and then a peak-finding algorithm identifies the grid nodes (Methods). After this determination of grid geometry, within each image tile the fluorescence signals are re-assigned to the center of the tile. Next, to computationally correct for fluorescence scattering across nearby image tiles, the fluorescence signals assigned to each image tile undergo a blind un-mixing, using an un-mixing matrix that is initialized with the pi,j matrices determined in Supplementary Fig. 8d. After un-mixing, the resulting signals are re-mapped from each image tile back into a representation of the specimen plane. After this procedure is applied to each image sub-sample, the entire image is reconstructed by summing the results obtained from all the sub-samples. (d) Example images processed using each of the methods outlined in panels a–c, for cells expressing tdTomato imaged in fixed brain slices at three different depths in tissue. Reconstruction Methods 1 and 2 improved image contrast by 310 ± 130% (s.d.) and 310 ± 190%, respectively, as determined on a set of 59 different images acquired in fixed brain tissue slices with neurons expressing tdTomato, YFP or GCaMP6f, across a range of tissue depths from 0–615 μm beneath the tissue surface. Scale bars: 50 μm in a–c and 25 μm in d.
Supplementary Figure 10 Improving image contrast by desynchronizing laser pulses across the beamlet array.
(a) Schematic illustrating the approach to imaging taken elsewhere in the paper, using ultrashort-pulses of illumination synchronized in time and with uniform intensity across the different laser beamlets emerging from the microlens array (MLA). (b) Schematic of an approach to reduce background fluorescence caused by interference between the different beamlets that leads to fluorescence excitation outside the focal plane. The method involves desynchronization of the ultrashort-laser pulses in the different beamlets8, but unlike prior means of desynchronization that involved insertion into the optical pathway of temporal delay masks with a spatial periodicity equal to a multiple of that of the beamlet array, the approach here uses masks with a pseudo-random spatial arrangement of the temporal delays imposed on the different beamlets. A stack of multiple glass plates of equal thickness, d, is placed in front of the microlens array. Each plate contains a different pseudo-randomly arranged set of square holes, with each hole aligned to the center of one of the microlenses. Together, the stack of plates impose a varied set of temporal delays on the different beamlets. Specifically, if one beamlet passes through k fewer pieces of glass than another, the net delay between the two beamlets is k(n–1)d/c, where τ = (n–1)d/c is the relative delay introduced by a single glass plate of refractive index, n, and c is the speed of light. For pulse desynchronization in panels e–g there were 6 glass plates, each of 170 µm thickness, which yielded a net range of temporal delays from 0–1680 fs in 7 equally spaced increments of τ = 280 fs per plate. (c) Left, An example design of one of the glass plates and its set of cut holes. Each plate had square holes in assorted locations, and each hole covered 9 beamlets. The sides of the square holes were separated by no less than one row or column of beamlets. Circular cutouts facilitate alignment. Middle, Photograph of the actual glass plate with the design shown. Right, A map of the temporal delays produced by the example plate. Scale bars: 2 mm. (d) Left, A schematic showing that by stacking 6 plates with different patterns of holes, we created a pseudo-random spatial arrangement of temporal delays for the different beamlets. Middle, Diagrams of the hole patterns for the 6 plates. Right, Spatial map of the optical delays achieved by stacking the 6 example plates. The delays ranged from 0–1680 fs, in equal increments of τ = 280 fs. (e) Assessments of the effects of beamlet desynchronization, performed by two-photon imaging in fixed brain slices (550 μm thick) from a mouse line (GCaMP6f-tTA-dCre) with fluorescently labeled pyramidal cells. The panel shows maximum projections of three-dimensional image stacks acquired at the same tissue location over an axial range of 0–200 μm from the tissue surface, with and without beamlet desynchronization, and with and without computational spatial bandpass filtering of the individual image slices. Scale bars: 30 μm. (f) Quantifications of the reduction in background fluorescence achieved via laser pulse desynchronization. A slide with a 1–2 μm thick, uniform fluorescent layer was placed into the path of laser beamlets and permitted characterizations of the fluorescence emission patterns with (blue curves) and without (red curves) use of the temporal delay mask. Dashed and solid curves show, respectively, the fluorescence generated on a beamlet-axis, and the net fluorescence integrated laterally across each lateral plane, plotted as a function of the fluorescent slide’s axial displacement from the plane of the laser foci. (g) Assessments of how the measurements in f were affected by placing unlabeled brain tissue slices atop the fluorescent slide to induce forward scattering of the excitation beams and thereby to increase the extent of optical interference outside the focal plane. Blue and red curves respectively show the net fluorescence integrated laterally across each lateral plane, with and without use of the temporal delay mask. Each curve is an average of the data obtained from 3 different brain slices.
Supplementary Information
Supplementary Information
Supplementary Figs. 1–10.
Supplementary Video 1
In vivo two-photon imaging of neocortical arteriolar microcirculation at a 100 Hz frame acquisition rate. Intracardially injected, fluorescently labeled HEK-293 cells flow in neocortical arterioles in the motor cortex of an anesthetized mouse. By using high-speed two-photon imaging, we acquired video frames at 100 Hz across a 450 × 300 µm2 field of view, corresponding to 700 × 472 pixels on the camera. Each of the 20 × 20 laser beamlets had 2.2 mW average power at the specimen plane. Scale bar, 50 μm.
Supplementary Video 2
In vivo two-photon imaging of neocortical microcirculation at a 1 kHz frame acquisition rate. Intracardially injected, fluorescently labeled HEK-293 cells flow in a cerebral artery of an anesthetized mouse. By using high-speed two-photon imaging, we acquired video frames at 1000 Hz. Each of the 20 × 0 laser beamlets had 2.9 mW mean power at the specimen plane. Due to limitations on data throughput set by the camera, the field of view at 1 kHz data acquisition was 450 × 110 μm2, corresponding to 700 × 172 camera pixels. For display purposes, the movie has been further cropped to 325 × 105 μm2. Note the rhythmic increases and decreases in flow speed. Scale bar, 50 μm.
Supplementary Video 3
High-speed in vivo two-photon imaging of neural calcium dynamics at a 1 kHz frame acquisition rate in an awake mouse. Somatic calcium activity of neocortical layer 2/3 pyramidal cells, ~100 µm deep in tissue, in an awake GCaMP6f-tTA-dCre mouse. The video shows 30 s of neural activity, played back at 3× real speed. The illumination beamlets had mean power levels of 0.5 mW (pulse repetition rate, 50 kHz). Scale bar, 20 µm.
Rights and permissions
About this article
Cite this article
Zhang, T., Hernandez, O., Chrapkiewicz, R. et al. Kilohertz two-photon brain imaging in awake mice. Nat Methods 16, 1119–1122 (2019). https://doi.org/10.1038/s41592-019-0597-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41592-019-0597-2
This article is cited by
-
Cortex-wide transcranial localization microscopy with fluorescently labeled red blood cells
Nature Communications (2024)
-
High-speed low-light in vivo two-photon voltage imaging of large neuronal populations
Nature Methods (2023)
-
A Through-Intact-Skull (TIS) chronic window technique for cortical structure and function observation in mice
eLight (2022)
-
Two-photon calcium imaging of neuronal activity
Nature Reviews Methods Primers (2022)
-
Multiregion neuronal activity: the forest and the trees
Nature Reviews Neuroscience (2022)