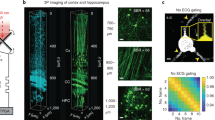
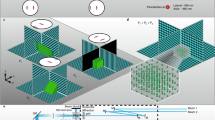
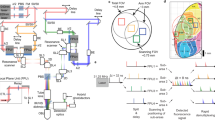
Abstract
Point-scanning two-photon microscopy enables high-resolution imaging within scattering specimens such as the mammalian brain, but sequential acquisition of voxels fundamentally limits its speed. We developed a two-photon imaging technique that scans lines of excitation across a focal plane at multiple angles and computationally recovers high-resolution images, attaining voxel rates of over 1 billion Hz in structured samples. Using a static image as a prior for recording neural activity, we imaged visually evoked and spontaneous glutamate release across hundreds of dendritic spines in mice at depths over 250 µm and frame rates over 1 kHz. Dendritic glutamate transients in anesthetized mice are synchronized within spatially contiguous domains spanning tens of micrometers at frequencies ranging from 1–100 Hz. We demonstrate millisecond-resolved recordings of acetylcholine and voltage indicators, three-dimensional single-particle tracking and imaging in densely labeled cortex. Our method surpasses limits on the speed of raster-scanned imaging imposed by fluorescence lifetime.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
Optical and mechanical designs and instructions for use are available through the Janelia Open Science portal at www.janelia.org/open-science. Example data sets and demonstrations, are available in Supplementary Software 1, and at www.github.com/KasparP/SLAP. All other resources and data are available from the corresponding author upon reasonable request.
Code availability
Software was written in MATLAB (R 2015b–2018b), C and LabView FPGA. Custom code used for microscope control, data processing, analysis and simulations are available in Supplementary Software 1, and at www.github.com/KasparP/SLAP. All other custom code is available from the corresponding author upon reasonable request.
Change history
06 August 2019
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Yang, W. & Yuste, R. In vivo imaging of neural activity. Nat. Methods 14, 349–359 (2017).
Sofroniew, N. J., Flickinger, D., King, J. & Svoboda, K. A large field of view two-photon mesoscope with subcellular resolution for in vivo imaging. eLife 5, e14472 (2016).
Peterka, D. S., Takahashi, H. & Yuste, R. Imaging voltage in neurons. Neuron 69, 9–21 (2011).
Prevedel, R. et al. Fast volumetric calcium imaging across multiple cortical layers using sculpted light. Nat. Methods 13, 1021–1028 (2016).
Chen, X., Leischner, U., Rochefort, N. L., Nelken, I. & Konnerth, A. Functional mapping of single spines in cortical neurons in vivo. Nature 475, 501–505 (2011).
Strickler, S. J. & Berg, R. A. Relationship between absorption intensity and fluorescence lifetime of molecules. J. Chem. Phys. 37, 814–822 (1962).
Sobczyk, A., Scheuss, V. & Svoboda, K. NMDA receptor subunit-dependent [Ca2+] signaling in individual hippocampal dendritic spines. J. Neurosci. 25, 6037–6046 (2005).
Hao, J. & Oertner, T. G. Depolarization gates spine calcium transients and spike-timing-dependent potentiation. Curr. Opin. Neurobiol. 22, 509–515 (2012).
Pnevmatikakis, E. A. & Paninski, L. Sparse nonnegative deconvolution for compressive calcium imaging: algorithms and phase transitions. In Advances in Neural Information Processing Systems Vol. 26 (eds Burges, C. J. C. et al.) 1250–1258 (Curran Associates, Inc., 2013).
Pnevmatikakis, E. A. et al. Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron 89, 285–299 (2016).
Szalay, G. et al. Fast 3D imaging of spine, dendritic, and neuronal assemblies in behaving animals. Neuron 92, 723–738 (2016).
Bullen, A., Patel, S. S. & Saggau, P. High-speed, random-access fluorescence microscopy: I. high-resolution optical recording with voltage-sensitive dyes and ion indicators. Biophys. J. 73, 477–491 (1997).
Yang, W. et al. Simultaneous multi-plane imaging of neural circuits. Neuron 89, 269–284 (2016).
Lu, R. et al. Video-rate volumetric functional imaging of the brain at synaptic resolution. Nat. Neurosci. 20, 620–628 (2017).
Song, A. et al. Volumetric two-photon imaging of neurons using stereoscopy (vTwINS). Nat. Methods 14, 420–426 (2017).
Botcherby, E. J., Juškaitis, R. & Wilson, T. Scanning two photon fluorescence microscopy with extended depth of field. Opt. Commun. 268, 253–260 (2006).
Thériault, G., Cottet, M., Castonguay, A., McCarthy, N. & De Koninck, Y. Extended two-photon microscopy in live samples with Bessel beams: steadier focus, faster volume scans, and simpler stereoscopic imaging. Front. Cell. Neurosci. 8, 139 (2014).
Field, J. J. et al. Superresolved multiphoton microscopy with spatial frequency-modulated imaging. Proc. Natl Acad. Sci. USA 113, 6605–6610 (2016).
Richardson, W. H. Bayesian-based iterative method of image restoration. JOSA 62, 55–59 (1972).
Lucy, L. B. An iterative technique for the rectification of observed distributions. Astron. J. 79, 745 (1974).
Neil, Ma. A., Juškaitis, R. & Wilson, T. Method of obtaining optical sectioning by using structured light in a conventional microscope. Opt. Lett. 22, 1905–1907 (1997).
Gustafsson, M. G. Extended resolution fluorescence microscopy. Curr. Opin. Struct. Biol. 9, 627–628 (1999).
Preibisch, S. et al. Efficient Bayesian-based multiview deconvolution. Nat. Methods 11, 645–648 (2014).
Broxton, M. et al. Wave optics theory and 3-D deconvolution for the light field microscope. Opt. Express 21, 25418–25439 (2013).
Antipa, N. et al. DiffuserCam: lensless single-exposure 3D imaging. Optica 5, 1–9 (2018).
Prevedel, R. et al. Simultaneous whole-animal 3D imaging of neuronal activity using light-field microscopy. Nat. Methods 11, 727–730 (2014).
Brown, G. D., Yamada, S. & Sejnowski, T. J. Independent component analysis at the neural cocktail party. Trends Neurosci. 24, 54–63 (2001).
Candes, E. J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 346, 589–592 (2008).
Lustig, M., Donoho, D. & Pauly, J. M. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007).
Pégard, N. C. et al. Compressive light-field microscopy for 3D neural activity recording. Optica 3, 517–524 (2016).
Chen, G.-H., Tang, J. & Leng, S. Prior image constrained compressed sensing (PICCS): a method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med. Phys. 35, 660–663 (2008).
von Diezmann, A., Shechtman, Y. & Moerner, W. E. Three-dimensional localization of single molecules for super-resolution imaging and single-particle tracking. Chem. Rev. 117, 7244–7275 (2017).
Kazemipour, A., Babada, B., Wu, M., Podgorski, K. & Druckmann, S. Multiplicative updates for optimization problems with dynamics. In 51st Asilomar Conference on Signals, Systems, and Computers (ed. Matthews, M. B.) 2025–2029 (IEEE, 2017).
Marvin, J. S. et al. Stability, affinity, and chromatic variants of the glutamate sensor iGluSnFR. Nat. Methods 15, 936 (2018).
Deal, P. E., Kulkarni, R. U., Al-Abdullatif, S. H. & Miller, E. W. Isomerically pure tetramethylrhodamine voltage reporters. J. Am. Chem. Soc. 138, 9085–9088 (2016).
Gray, E. G. Electron microscopy of synaptic contacts on dendrite spines of the cerebral cortex. Nature 183, 1592–1593 (1959).
Mainen, Z. F., Malinow, R. & Svoboda, K. Synaptic calcium transients in single spines indicate that NMDA receptors are not saturated. Nature 399, 151–155 (1999).
Mayer, M. L., Westbrook, G. L. & Guthrie, P. B. Voltage-dependent block by Mg2+ of NMDA responses in spinal cord neurones. Nature 309, 261–263 (1984).
Chen, T.-W. et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300 (2013).
Dana, H. et al. Sensitive red protein calcium indicators for imaging neural activity. eLife 5, e12727 (2016).
Tan, A. Y. Y., Brown, B. D., Scholl, B., Mohanty, D. & Priebe, N. J. Orientation selectivity of synaptic input to neurons in mouse and cat primary visual cortex. J. Neurosci. 31, 12339–12350 (2011).
Jensen, T. P. et al. Multiplex imaging relates quantal glutamate release to presynaptic Ca2+ homeostasis at multiple synapses in situ. Nat. Commun. 10, 1414 (2019).
Nahum-Levy, R., Tam, E., Shavit, S. & Benveniste, M. Glutamate but not glycine agonist affinity for NMDA receptors is influenced by small cations. J. Neurosci. 22, 2550–2560 (2002).
Harris, K. D. & Thiele, A. Cortical state and attention. Nat. Rev. Neurosci. 12, 509–523 (2011).
Luczak, A., Bartho, P. & Harris, K. D. Gating of sensory input by spontaneous cortical activity. J. Neurosci. 33, 1684–1695 (2013).
Stringer, C. et al. Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, eaav7893 (2019).
Buzsáki, G., Logothetis, N. & Singer, W. Scaling brain size, keeping timing: evolutionary preservation of brain rhythms. Neuron 80, 751–764 (2013).
Cohen, M. R. & Maunsell, J. H. R. Attention improves performance primarily by reducing interneuronal correlations. Nat. Neurosci. 12, 1594–1600 (2009).
Yamamoto, J., Suh, J., Takeuchi, D. & Tonegawa, S. Successful execution of working memory linked to synchronized high-frequency gamma oscillations. Cell 157, 845–857 (2014).
Zucca, S. et al. An inhibitory gate for state transition in cortex. eLife 6, e26177 (2017).
Constantinople, C. M. & Bruno, R. M. Effects and mechanisms of wakefulness on local cortical networks. Neuron 69, 1061–1068 (2011).
Okun, M. et al. Population rate dynamics and multineuron firing patterns in sensory cortex. J. Neurosci. 32, 17108–17119 (2012).
Xie, Y. et al. Resolution of high-frequency mesoscale intracortical maps using the genetically encoded glutamate sensor iGluSnFR. J. Neurosci. 36, 1261–1272 (2016).
Schuett, S., Bonhoeffer, T. & Hübener, M. Mapping retinotopic structure in mouse visual cortex with optical imaging. J. Neurosci. 22, 6549–6559 (2002).
Wu, J. et al. Kilohertz in vivo imaging of neural activity. Preprint at bioRxiv https://doi.org/10.1101/543058 (2019).
Laissue, P. P., Alghamdi, R. A., Tomancak, P., Reynaud, E. G. & Shroff, H. Assessing phototoxicity in live fluorescence imaging. Nat. Methods 14, 657–661 (2017).
Podgorski, K. & Ranganathan, G. Brain heating induced by near-infrared lasers during multiphoton microscopy. J. Neurophysiol. 116, 1012–1023 (2016).
Brainard, D. H. The psychophysics toolbox. Spat. Vis. 10, 433–436 (1997).
Sommer, C., Straehle, C., Köthe, U. & Hamprecht, F. A. Ilastik: Interactive learning and segmentation toolkit. In 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro (eds Wright, S. et al.) 230–233 (2011).
Sakoe, H. & Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 26, 43–49 (1978).
Podgorski, K. & Haas, K. Fast non-negative temporal deconvolution for laser scanning microscopy. J. Biophotonics 6, 153–162 (2013).
Acknowledgements
E.W.M., P.E.D. and S.H.A. acknowledge funding support from the following sources: National Institutes of Health (R35GM119855, R01NS098088), National Science Foundation (NeuroNex 1707350) and the Klingenstein-Simons Fellowship Award in Neurosciences. Work by the remaining authors was funded by the Howard Hughes Medical Institute. The authors thank H. Davies for logistical support; S. Dilisio, J. Hagemeier, A. Hu, B. Shields, D. Walpita and O. Zelenka for experimental support; V. Goncharov, S. Sawtelle, C. McRaven, N. Ji, A. Kerlin, J. Little, B. Mensh, B. Mohar, M. Mohr, M. Pachitariu, C. Stringer and S. Turaga for discussions and comments on the manuscript.
Author information
Authors and Affiliations
Contributions
A.K. designed solvers, performed the simulations, designed experiments, conducted data analysis, and contributed manuscript writing and figures. O.N. contributed surgeries and designed experiments. D.F. performed optical and mechanical design. J.S.M., P.M.B. and L.L.L. conducted the protein engineering. J.K. conducted the FPGA programming and contributed to microscope control software. J.J.K. conducted motion tracking experiments. S.A., P.E.D. and E.W.M conducted voltage indicator design and synthesis. A.A. and E.R.S. designed and performed voltage indicator experiments. S.D. and K.S. contributed to experimental design. K.P. came up with the concept, designed and performed experiments, and worked on optical design, mechanical design, electronics, microscope control software, microscope construction, surgeries, solvers, data analysis, writing the manuscript and producing the figures.
Corresponding author
Ethics declarations
Competing interests
A.K., D.F. and K.P. are listed as inventors on a patent application No. 62/502,643 claiming SLAP, filed by HHMI.
Additional information
Peer review information: Nina Vogt was the primary editor on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Integrated supplementary information
Supplementary Figure 1 Measured Point Spread Functions.
R-Z (lateral-axial) images of 200nm beads obtained with SLAP’s line scan (top left) and raster scan modes (top center). The full-width half-maximum extents of the PSFs are: Raster beam: 415 nm X, 1469 nm Z Line beam: 432 nm X, 1617 nm Z Without correction for the size of the bead. The corresponding diffraction limit for a point source is 377nm X, 1423nm Z (Zipfel et al., 2003). Line excitation results in slightly reduced axial sectioning because light is focused on only one lateral axis. As a result, the total intensity of the line focus decreases as 1/z away from the focal point, compared to 1/z2 for the point focus, where z is axial distance from the focal plane. Subtraction of the raster and line PSF highlights the axial side lobes in the line PSF (top right). We incorporate a discrete convolution when using the image obtained with the raster beam to estimate measurements under the line beams, to account for these side lobes. The convolution kernel (example, bottom center) is estimated by deconvolving the line PSF with the raster PSF and constraining the solution (bottom left) to be positive and lie within the plane spacing of the reference image (0.75 µm). The raster PSF convolved with this kernel agrees well with the line PSF. Use of this model PSF improves agreement between expected and measured SLAP recordings (Supplementary Fig. 6j).
Supplementary Figure 2 SLAP Excitation Efficiency.
a) Excitation efficiency (the number of fluorescence photons collected as a function of average excitation power) for SLAP and raster scanning, measured for fields of view with different degrees of sparsity. Recordings were performed in a fluorescent plastic block (Chroma Technologies), with sparsity artificially imposed using the SLM. Photon rates were measured by summing photodetector current and dividing by the known mean current for a single photon. Lines are quadratic fits (forced 0-intercept) to the measured points. b) Power required to achieve a brightness of 10,000 photons per second per square micron, for SLAP and raster scanning, computed from quadratic fits in (a). The power required by conventional raster scanning is independent of the sample. The power required by SLAP is linear in the SLM open area, with non-zero intercept due to the imperfect extinction of excitation light by ‘OFF’ pixels of the SLM. SLAP and raster scanning have equal efficiencies for fields of view with approximately 2% of pixels labelled. SLAP efficiency could be further improved by increasing the extinction of the SLM. Experiment was performed once.
Supplementary Figure 3 Automated Segmentation.
The goal of the automated segmentation procedure is to group pixels such that each segment within the SLM ‘ON’ area belongs to a single neuronal compartment (such as a spine), all segments are of a minimum integrated brightness, and the total number of compartments within the SLM ‘ON’ area is less than 1000. These constraints can only be approximately satisfied. To do this, the reference volume (left, gamma=0.5; small region shown for clarity) is classified into 4 classes (center) using a hand trained classifier in Ilastik’s autocontext mode. The classes are correspond to dark (background) voxels, spine heads, voxels with fluorescent label, and dendritic shafts. The voxel classes and image intensity are passed to a skeletonization-based algorithm that groups non-dark pixels into segments. The automated segmentation output (right) occasionally produces flaws such as fused or split spines, which have not yet been quantified. We have written an interface (segEdit in the software package) for manual curation of these errors, which was used for most datasets. This example automated segmentation is typical of all yGluSnFR fields of view imaged.
Supplementary Figure 4 Simulations of SLAP activity reconstruction.
We evaluated solver performance by reconstructing simulated data under a variety of conditions. The measurement parameters in these simulations were chosen to match our 1016 Hz imaging experiments. To assess sensitivity of source recovery to solver/simulation parameters, we modified each parameter while holding the others constant. In panels A,B, and H, the simulated sample consisted of numerous square segments (10*10 pixels) placed randomly (uniformly chosen) within a 500 pixel diameter. In the remaining panels, the simulated sample was generated from a segmented yGluSnFR-labeled volume from one of our experiments. Peak ΔF/F0 for each segment was uniformly distributed in the interval [0.5, 5]. We performed 500 iterations of the dynamic Richardson Lucy algorithm, or normal Richardson Lucy deconvolution for comparison, where stated. To evaluate performance, we calculated the Pearson correlation between the estimated ΔF/F0 trace and its ground-truth counterpart over time for each segment, averaged over segments. a. Effect of sample brightness on imaging performance. The expected Poisson-distributed photon rates per segment per frame was varied, in the range 0.1-105. Typical values of this parameter in the recorded datasets in this work are around 100. Recovery improves at higher photon rates. b. Effect of number of sources on imaging performance. The number of sources was varied, in the range 10-1000, in both the generation of ground truth data and the segmentation algorithm. Increasing the number of sources decreases solver performance. c. Effect of incorrectly-estimated decay time constant. The ground truth activity was generated using a time constant of 100 frames. The time-constant of source recovery was varied in the range 0-1000. The solver performs best when the correct time constant is used. The solver is insensitive to underestimation of the time-constant, as this can be compensated with additional spikes (w) but does reduce the denoising benefit of the dynamics model. A time constant of 0 corresponds to normal Richardson-Lucy iterations. Substantial overestimation of the time constant degrades performance of the solver. d. Effect of incorrect reference image. We evaluated the performance of the solver in the case where ground truth sources were omitted from the segmentation. We added 0-50% additional unsegmented sources, while quantifying reconstruction performance over the segmented sources. This is meant to simulate fluorescence activity within the ‘ON’ region of the SLM not reflected in the reference image, a possibility in sensors with very low baseline fluorescence. Increasing unsegmented activity degrades the performance of the solver. e. Effect of alignment errors. We shifted the reference image provided to the solver by 0-10 pixels, after registration. Better alignment improves the reconstructions. f. Effect of segmentation spatial scale. We performed source recovery using finer or coarser segmentations than those used to generate the data. Segmentation differing from the ground truth degrade performance, which can be partially compensated for by using a finer segmentation scale. g. Estimation of pairwise correlations. In each simulation, we generated 3000 frames of correlated random spike amplitudes (w) using vines and the extended onion method41, to which we applied the dynamics model to produce ground truth ΔF/F0 timeseries with source-to-source correlations in the range [−0.6 0.6]. Measurements were simulated from these ground truth traces and reconstructed. Plotted are pairwise correlation coefficients in the ground truth vs. reconstructed data using (left) normal RL iterations or (right) Dynamic RL iterations. h. SLAP performance with different numbers of tomographic angles. We simulated the performance of SLAP source recovery with different numbers of equally-spaced line angles, at two different sample densities. At the higher sample density (500 sources), increasing the number of line angles from four to 8 improved performance, equivalent to approximately doubling the photon rate. At the lower sample density (100 sources), the corresponding improvement was negligible. Parameters settings for the above experiments: # random instances: A,G:5 B,C,D,E,H:40; F:10. # frames per instance: A,B,E: 350 ; B,C,F,H:500 G: 3000. # segments: A,C,E,G: 500 ; Photons per frame per segment: B-F: 100. τ: 100
Supplementary Figure 5 In Vitro Voltage Imaging.
a) Hippocampal culture labeled with RhoVR.pip.sulf. Dashed lines denote fields of view recorded by fast widefield and SLAP imaging. b) ΔF/F0 traces for the neuron outlined in (a) using two-photon SLAP without a dynamics prior (τ=0, top) or one-photon widefield imaging (bottom), in separate trials. Suprathreshold field stimuli (90 V/cm; black arrowheads) were applied to evoke action potentials. (right) Zoom of the red boxes in b. (c-e) FOV containing multiple neuron somata. Low-amplitude field stimuli (50 V/cm; black arrowheads) were applied to produce asynchronous spike patterns. Widefield imaging frame rate was limited to 400 Hz due to the size of the FOV. e) Scatterplot of SLAP responses of the two cells, demonstrating distinct patterns of firing in the two neurons. Amplitudes were the sum ΔF/F0 in the 20 ms following each stimulus, divided by the mean of the 3 largest amplitudes per recording. d’ values were calculated by fitting two Gaussians of equal variance (dotted lines) to the marginal activity distribution for each neuron (histograms). The cell outlines in (a,c) denote ROIs used to generate traces, by pixel-averaging (widefield) or frame-independent nonnegative unmixing (SLAP). Imaging power: 31 mW two-photon, 0.7 mW one-photon. These powers were the maximum that did not result in noticeable photobrightening of the voltage indicator, which occurs at higher excitation powers in both modalities. (a-d) We recorded 16 fields of view with similar results.
Supplementary Figure 6 SLAP motion tracking and registration.
Reconstruction of SLAP data requires precise and accurate detection of sample position, and appropriate compensation by the imaging model. We perform motion registrations using 3D grid search to identify the sample displacement that minimizes an alignment cost function (Methods). (a-e) We characterized registration precision by introducing known 3D displacements to a static sample of beads embedded in agarose gel. X-Y displacements were made by moving the stage and collecting a raster image to determine the precise lateral displacement. Axial displacements were made with a calibrated piezo objective stage. As in all experiments, 2D SLAP frames are aligned in 3D to a 3D reference image. b) Actual vs. estimated displacements from center of reference image for lateral (X,Y) axes. ‘Actual’ displacements were computed from raster scan images acquired after each stage movement. c) Histogram of alignment errors when aligning single SLAP frames (top) or mean of 100 frames (bottom). Lateral alignments were performed at 50 nm grid spacing. d) Actual vs. estimated displacements from center of reference image for vertical (Z) axis. e) Histogram of alignment errors for single SLAP frames (top) or mean of 100 SLAP frames (bottom). Axial alignments were performed at 375 nm grid spacing. (f-i) We demonstrated kHz-framerate sub-micron 3D brain motion tracking in awake headfixed mice implanted with fluorescent beads. g) Example SLAP recording. Despite head fixation, significant brain motion occurs during movements. Dashed boxes denote zoomed regions at right. h) Estimated 3D displacements for the same recording. i) Histograms of frame-to-frame displacements. Each frame was aligned independently to the 3D reference image. Estimated displacements between consecutive frames never exceeded a single pixel of the reference image (200nm lateral, 750 nm axial; frames were aligned at 0.5 pixel precision, n=2000 frames). This indicates that sample motion within a single 1-ms frame is negligible even in actively moving mice, and that SLAP motion alignment is precise and reliable. (f-i) this experiment was repeated 5 times in 2 mice with similar results. j) SLAP measurements (average of 100 frames) and Expected SLAP measurements before (left) and after (right) global position alignment. The Expected measurement is the product of the measurement matrix (P) with the rigidly-aligned reference image. This example is typical of all in vivo recordings in the study.
Supplementary Figure 7 Simultaneously recorded yGluSnFR and jRGECO traces (related to Fig. 4).
a) Representative traces over eight consecutive stimuli from Spine and Shaft ROIs of Fig. 4b. b) Mean temporal responses and tuning curves for the same ROIs (N = 20 trials per stimulus). Markers denote mean +/- SEM.
Supplementary Figure 8 High-frequency signals in dendritic yGluSnFR recordings.
We compared power spectra of yGluSnFR and dead sensor recordings to those expected by chance using a Monte Carlo framework. Our null hypothesis was that signals have no power at frequencies above 15 Hz (orange shading; the maximum signal frequency detectable by video-rate 30Hz imaging), and that measured modulation above this frequency results solely from shot noise and the source recovery process. We calculated the null distribution by low-pass filtering (8th-order Butterworth filter, 15Hz cutoff) the recovered rates (X) for each segment and generating Poisson samples from these filtered rates to produce simulated recordings. We performed source recovery on the simulated recordings in the same way as the original recordings, producing a null distribution of recovered traces. We scaled each trace in the simulated recordings so the average power below 15Hz was equal to that in the original recording. We then compared the measured power spectra of the most motion-tuned segments in each FOV to their power spectra under the null (shown is the mean ratio +/- s.e.m; N=10 fields of view yGluSnFR, N=4 fields of view Dead Sensor). Segments were selected for inclusion as in analyses for Fig. 6 (see Methods: Analysis of In Vivo Recordings). The mean power ratio of yGluSnFR.A184S vs null recordings was larger than dead sensor controls at frequencies above 15 Hz (p=0.02, two-sided two-sample t-test). The mean power ratio of the dead sensor recordings did not significantly differ from unity above 15Hz (p = 0.69, two-sided one-sample t-test), indicating that these signals do not contain significant high-frequency components. The mean power ratio of yGluSnFR recordings was significantly greater than unity for all frequencies between 15 and 137 Hz (p<0.05, two-sided one-sample t-test).
Supplementary Figure 9 Conservations of global modes across stimuli.
(top) Pearson correlations between PCA spatial modes computed separately for each stimulus type (N= 8 trials per stimulus). High correlations indicate similar spatial patterns. The largest modes have similar spatial patterns for all stimuli. (bottom) Correlation of the temporal profile of each mode to inferred sample motion. These example data are from a single session. Results were similar for all 10 sessions recorded.
Supplementary Figure 10 Synchrony of glutamate transients measured by raster scanning.
We performed high speed raster scanning of yGluSnFR activity to compare signals with SLAP imaging (Fig. 6). a) Emx1-IRES-Cre transgenic mice were injected with 5x1011 gc/ml AAV2/1.Syn.FLEX-yGluSnFR.A184S into visual cortex (40nL per site, 300 um deep), resulting in dense labeling of excitatory neurons. We performed strip-shaped two photon raster scan recordings (2.33 x 100 um, 8x300 pixels, 222.2Hz, 4 sec duration, 35-38 mW power) at various angles within the focal plane, 85-110um below dura, while presenting visual motion stimuli as in our other experiments. Recordings were motion-registered, and any with displacements greater than 2 pixel along the short axis of the strip were discarded. 10µm x 1.33µm regions of interest were defined along the strip ((b, left); 9 ROIs across the strip; edges were discarded). (b,right) Example trial, demonstrating both shared and local ΔF/F0 transients across ROIs. Transients were not correlated to sample motion (bottom). c) Normalized shuffle-subtracted correlations (errorbars denote S.E.M.) binned by pairwise distance between ROIs, for SLAP and strip scanning. Normalization consisted of subtracting the mean pairwise correlation among shuffled pairs over the distance range supported by the strip scans (0-80um) for each session, and division by the standard deviation across bins. Mean correlations prior to normalization were 0.34 (raster), 0.38 (SLAP). Pairwise instantaneous correlations measured by both methods show distance-dependence over tens of microns. Raster: N = 3 mice, 154 strips. SLAP: N = 10 sessions.
Supplementary Figure 11 Orientation tuning of spatial modes.
Orientation tuning index of the largest NMF mode for each SLAP recording (10 sessions), and the null distribution obtained by shuffling stimulus labels. Some modes are strongly tuned while others are not. Markers denote mean. Errorbars denote standard deviation of the shuffle distribution. **: p=2.5e-4, Fisher’s combined test.
Supplementary Figure 12 Recording and localization of sparse AChSnFR responses in densely labeled cortex.
a) SLAP measurements from visual cortex densely labeled with yAChSnFR, 300 µm below the brain surface. A single electrical pulse (500 µA, 1 ms) was delivered to nucleus basalis at time 0. Red circles highlight fluorescence transients in the four projection axes following stimulation. b) (top) Magnified view of stimulus-induced transient. (bottom) ΔF/F0 traces for same region, over 6 consecutive trials. Dark line denotes mean, light lines denote trials. c) Backprojection of the locations in (a) onto raster image of the FOV reveals the spatial origin of the transients. SLAP excitation power: 308 mW, depth 300 µm. Experiment was performed for 7 FOVs (one mouse) with similar results.
Supplementary Figure 13 SiPM detector performance.
Our SLAP microscope uses Silicon Photomultiplier (SiPM) photodetectors. (a) Zoom of detector voltage trace during a SLAP acquisition. Digitization (250 MHz) is synchronized to laser emission (5 MHz) via a phase-locked loop. In response to each laser pulse, an integer number of photons arrives at the detector, resulting in spikes with distinct response amplitudes. (b) Histogram of detector response amplitudes, normalized to the amplitude of a single photon. This spectrum shows distinct peaks corresponding to the integer numbers of photons produced by each laser pulse, demonstrating the extremely uniform pulse height distribution and linear summation of pulses by SiPMs. The pulse height spectrum for a photomultiplier tube, by comparison, does not show distinguishable peaks for more than 2 photoelectrons, and hybrid photodetectors represent a much smaller improvement in this respect (“Hybrid photodetectors combine PMT and semiconductor diode technologies.” Motohiro Suyama, Hamamatsu Photonics K.K., and Maridel Lares, Hamamatsu Corporation; 2008). Experiment was performed once.
Supplementary Figure 14 Neuronal morphology and response tuning before and 6 days after SLAP imaging.
An example L2/3 cortical neuron was imaged with SLAP for 64 trials at an average power of 87 mW on Day 1. Neuronal morphology (top) was imaged before SLAP recording (left) and in a second session 6 days later (right). Raster recordings of tuning (bottom) were interleaved with SLAP imaging on Day 1, and again 6 days later. We observed no signs of damage from SLAP imaging. Experiment was performed once.
Supplementary Figure 15 Characterization of RhoVR.Pip.Sulf 1.
(a) DIC image of cells loaded with RhoVR 1. (b) Fluorescence image of cells loaded with RhoVR 1. (c) DIC image of cells loaded with RhoVR.Pip.Sulf. (d) Fluorescence image of cells loaded with RhoVR.Pip.Sulf. Scale bar is 20 µm. (e) Quantification of relative RhoVR fluorescence in HEK cells. Bars denote mean ± S.D. for n = 4 (RhoVR 1) or 6 (RhoVR.Pip.Sulf) cells. (f) The fractional change in fluorescence is plotted vs. time for 100 ms hyper- and depolarizing steps (±100 mV, 20 mV increments) from a holding potential of -60 mV for a single HEK cells under whole-cell voltage-clamp mode. (g) A plot of % ΔF/F vs. final membrane potential (mV) summarizing data from 5 separate cells.
Supplementary information
Supplementary Information
Supplementary Figs. 1–15, Supplementary Notes 1–3 and Supplementary Table 1.
Supplementary Video 1: SLAP imaging schematic
SLAP scans line foci across the sample plane at four different angles. At any given time, one of four line foci illuminates the sample, generating a single measurement that corresponds to the combined brightness of the sample voxels along that line. Only regions in the sample plane selected by the SLM are illuminated. Remaining excitation light (darkened region) is discarded, thereby reducing sample heating and simplifying source recovery.
Supplementary Video 2: 3D SLAP measurements of flowing particles
Three-dimensional SLAP recording of a 250 × 250 × 250 µm3 volume (90 planes), imaged at a 10 Hz volume rate, containing flowing 0.5 µm fluorescent beads. Each recorded volume corresponds to four two-dimensional (X-Z) projections of the sample along the four distinct line axes.
Supplementary Video 3: 3D SLAP reconstruction of flowing particles
Volume video reconstructed from the measurements in Video 2 using Richardson–Lucy deconvolution.
Supplementary Video 4: In vitro recording of glutamate uncaging
SLAP activity recording of a yGluSnFR-expressing neuron. Glutamate was uncaged at two locations, 10 ms apart, at t = 800 ms. Saturation denotes ΔF/F0 conditioned on Z-score. Blue tinted regions were blocked by the SLM. Experiment was performed on 8 FOV with similar results.
Supplementary Video 5: In vivo yGluSnFR Raster Imaging
Two-photon raster recording of pyramidal neuron dendrites in mouse V1 expressing yGluSnFR.A184S. The mouse was shown eight directions of moving bar stimuli at the times indicated at bottom. Saturation denotes ΔF/F0 conditioned on Z-score. Experiment was performed on ten FOV (six mice) with similar results.
Supplementary Video 6: In vivo yGluSnFR SLAP Imaging
SLAP recording of the field of view shown in Supplementary Video 5. A moving bar stimulus was shown starting at t = 0 ms. Saturation denotes ΔF/F0 conditioned on Z-score. Experiment was performed on ten FOV (six mice) with similar results.
Supplementary Video 7: In vivo yGluSnFR-Null SLAP Imaging
SLAP recording of pyramidal neuron dendrites in mouse V1 expressing yGluSnFR-Null. A moving bar stimulus was shown starting at t = 0 ms. Saturation denotes ΔF/F0 conditioned on Z-score. Experiment was performed on four FOV (two mice) with similar results.
Supplementary Software
SLAP software. Code for acquiring and analyzing SLAP data, tutorials, and links to Demo data sets.
Rights and permissions
About this article
Cite this article
Kazemipour, A., Novak, O., Flickinger, D. et al. Kilohertz frame-rate two-photon tomography. Nat Methods 16, 778–786 (2019). https://doi.org/10.1038/s41592-019-0493-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41592-019-0493-9
This article is cited by
-
Live-cell imaging powered by computation
Nature Reviews Molecular Cell Biology (2024)
-
Cross-modality supervised image restoration enables nanoscale tracking of synaptic plasticity in living mice
Nature Methods (2023)
-
High-speed multiplane confocal microscopy for voltage imaging in densely labeled neuronal populations
Nature Neuroscience (2023)
-
Multifocal fluorescence video-rate imaging of centimetre-wide arbitrarily shaped brain surfaces at micrometric resolution
Nature Biomedical Engineering (2023)
-
An Algorithm Based on a Cable-Nernst Planck Model Predicting Synaptic Activity throughout the Dendritic Arbor with Micron Specificity
Neuroinformatics (2023)