Abstract
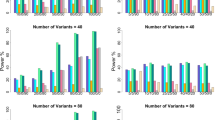
Family history of disease can provide valuable information in case–control association studies, but it is currently unclear how to best combine case–control status and family history of disease. We developed an association method based on posterior mean genetic liabilities under a liability threshold model, conditional on case–control status and family history (LT-FH). Analyzing 12 diseases from the UK Biobank (average N = 350,000) we compared LT-FH to genome-wide association without using family history (GWAS) and a previous proxy-based method incorporating family history (GWAX). LT-FH was 63% (standard error (s.e.) 6%) more powerful than GWAS and 36% (s.e. 4%) more powerful than the trait-specific maximum of GWAS and GWAX, based on the number of independent genome-wide-significant loci across all diseases (for example, 690 loci for LT-FH versus 423 for GWAS); relative improvements were similar when applying BOLT-LMM to GWAS, GWAX and LT-FH phenotypes. Thus, LT-FH greatly increases association power when family history of disease is available.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
This study analyzed data from the UK Biobank, which are publicly available by application (http://www.ukbiobank.ac.uk/). We have publicly released summary association statistics computed by applying our LT-FH method to UK Biobank data; LT-FH summary association statistics for 12 diseases are available at https://data.broadinstitute.org/alkesgroup/UKBB/LT-FH/sumstats/.
Code availability
We have publicly released open-source software implementing our LT-FH method; LT-FH software (v1 and v2): https://data.broadinstitute.org/alkesgroup/UKBB/LTFH/; BOLT-LMM v2.3 software: https://data.broadinstitute.org/alkesgroup/BOLT-LMM, LTSOFT software: https://data.broadinstitute.org/alkesgroup/LTSOFT/; and PLINK software: https://www.cog-genomics.org/plink2.
References
Liu, J. Z., Erlich, Y. & Pickrell, J. K. Case–control association mapping by proxy using family history of disease. Nat. Genet. 49, 325–331 (2017).
So, H.-C., Kwan, J. S. H., Cherny, S. S. & Sham, P. C. Risk prediction of complex diseases from family history and known susceptibility loci, with applications for cancer screening. Am. J. Hum. Genet. 88, 548–565 (2011).
Visscher, P. M. & Duffy, D. L. The value of relatives with phenotypes but missing genotypes in association studies for quantitative traits. Genet. Epidemiol. 30, 30–36 (2006).
Hayes, B. J., Bowman, P. J., Chamberlain, A. J. & Goddard, M. E. Genomic selection in dairy cattle: progress and challenges. J. Dairy Sci. 92, 433–443 (2008).
Misztal, I., Legarra, A. & Aguilar, I. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 92, 4648–4655 (2009).
Liu, Z., Goddard, M. E., Reinhardt, F. & Reents, R. A single-step genomic model with direct estimation of marker effects. J. Dairy Sci. 97, 5833–5850 (2014).
Marioni, R. E. et al. GWAS on family history of Alzheimer’s disease. Transl. Psychiatry 8, 99 (2018).
Jansen, I. E. et al. Genome-wide meta-analysis identifies new loci and functional pathways influencing Alzheimer’s disease risk. Nat. Genet. 51, 404–413 (2019).
Falconer, D. S. The inheritance of liability to diseases with variable age of onset, with particular reference to diabetes mellitus. Ann. Hum. Genet. 31, 1–20 (1967).
Lee, S. H., Wray, N. R., Goddard, M. E. & Visscher, P. M. Estimating missing heritability for disease from genome-wide association studies. Am. J. Hum. Genet. 88, 294–305 (2011).
Zaitlen, N. et al. Informed conditioning on clinical covariates increases power in case–control association studies. PLoS Genet. 8, e1003032 (2012).
Weissbrod, O., Lippert, C., Geiger, D. & Heckerman, D. Accurate liability estimation improves power in ascertained case–control studies. Nat. Methods 12, 332–334 (2015).
Hayeck, T. J. et al. Mixed model with correction for case–control ascertainment increases association power. Am. J. Hum. Genet. 96, 720–730 (2015).
Loh, P.-R. et al. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 47, 284–290 (2015).
Loh, P.-R., Kichaev, G., Gazal, S., Schoech, A. P. & Price, A. L. Mixed-model association for biobank-scale datasets. Nat. Genet. 50, 906–911 (2018).
Yang, J. et al. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 42, 565–569 (2010).
Pearson, K. Mathematical contributions to the theory of evolution. XI. On the influence of natural selection on the variability and correlation of organs. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 200, 1–66 (1903).
Aitken, A. C. Note on selection from a multivariate normal population. Proc. Edinb. Math. Soc. B 4, 106–110 (1934).
Armitage, P. Tests for linear trends in proportions and frequencies. Biometrics 11, 375–386 (1955).
Bycroft, C. et al. The UK Biobank resource with deep phenotyping and genomic data. Nature 562, 203–209 (2018).
Zhou, W. et al. Efficiently controlling for case–control imbalance and sample relatedness in large-scale genetic association studies. Nat. Genet. 50, 1335–1341 (2018).
Bulik-Sullivan, B. K. et al. LD score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 47, 291–295 (2015).
Finucane, H. K. et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat. Genet. 47, 1228–1235 (2015).
Gazal, S. et al. Linkage disequilibrium–dependent architecture of human complex traits shows action of negative selection. Nat. Genet. 49, 1421–1427 (2017).
Haworth, S. et al. Apparent latent structure within the UK Biobank sample has implications for epidemiological analysis. Nat. Commun. 10, 333 (2019).
Loh, P.-R. et al. Contrasting genetic architectures of schizophrenia and other complex diseases using fast variance components analysis. Nat. Genet. 47, 1385–1392 (2015).
Marigorta, U. & Navarro, A. High trans-ethnic replicability of GWAS results implies common causal variants. PLoS Genet. 9, e1003566 (2013).
Turley, P. et al. Multi-trait analysis of genome-wide association summary statistics using MTAG. Nat. Genet. 50, 229–237 (2018).
Price, A. L., Spencer, C. C. A. & Donnelly, P. Progress and promise in understanding the genetic basis of common diseases. Proc. Biol. Sci. 282, 20151684 (2015).
Visscher, P. M. et al. 10 years of GWAS discovery: biology, function, and translation. Am. J. Hum. Genet. 101, 5–22 (2017).
Manichaikul, A. et al. Robust relationship inference in genome-wide association studies. Bioinformatics 26, 2867–2873 (2010).
Munoz, M. et al. Evaluating the contribution of genetic and familial shared environment to common disease using the UK Biobank. Nat. Genet. 48, 980–983 (2016).
Schunkert, H. et al. Large-scale association analyses identifies 13 new susceptibility loci for coronary artery disease. Nat. Genet. 43, 333–338 (2011).
Morris, A. P. et al. Large-scale association analysis provides insights into the genetic architecture and pathophysiology of type 2 diabetes. Nat. Genet. 44, 981–990 (2012).
Michailidou, K. et al. Association analysis identifies 65 new breast cancer risk loci. Nature 551, 92–94 (2017).
Schumacher, F. et al. Association analyses of more than 140,000 men identify 63 new prostate cancer susceptibility loci. Nat. Genet. 50, 928–936 (2018).
Kichaev, G. et al. Leveraging polygenic functional enrichment to improve GWAS power. Am. J. Hum. Genet. 104, 65–75 (2019).
Acknowledgements
We are grateful to L. O’Connor, O. Weissbrod, N. Zaitlen, G. Kichaev and A. Gusev for helpful discussions and E.M. Pedersen for computational suggestions. This research was funded by NIH grants R01 HG006399 (N.P. and A.L.P.), R01 MH101244 (A.L.P.), R01 MH107649 (A.L.P.), NSF CAREER award DBI-1349449 (S.G. and A.L.P.) and 5T32CA009337-32 (M.L.A.H.). P.-R.L. was supported by the Next Generation Fund at the Broad Institute of MIT and Harvard and a Sloan Research Fellowship. This research was conducted using the UK Biobank resource under application no. 10438.
Author information
Authors and Affiliations
Contributions
M.L.A.H. and A.L.P. designed the experiments. M.L.A.H. performed the experiments and statistical analysis; N.P. assisted in proving the equivalence to a score test. M.L.A.H., S.G., P.-R.L. and A.L.P. analyzed the data. M.L.A.H. and A.L.P. wrote the manuscript with assistance from S.G., P.-R.L. and N.P.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 QQ plots from simulations with default parameter settings.
We report quantile-quantile (QQ) plots for null SNPs in simulations with default parameter settings. Results are based on 10 simulation replicates. These QQ plots compare the observed distribution of p-values with the standard uniform distribution. We plot the observed −log10(p) as a function of \(- \log _{10}\left( {\frac{{rank}}{{n + 1}}} \right)\) and the 95% confidence bands are constructed pointwise using the beta distribution.
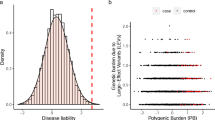
Extended Data Fig. 2 Distribution of LT-FH phenotypes for 12 UK Biobank diseases.
We plot the distribution of the LT-FH phenotype for each disease. We also report the kurtosis for both GWAS and LT-FH; Pearson’s measure of kurtosis, \(\kappa = \frac{{E\left[ {\left( {X - \mu } \right)^4} \right]}}{{\left( {E\left[ {\left( {X - \mu } \right)^2} \right]} \right)^2}}\), is calculated using the R package moments.
Extended Data Fig. 3 Impact of modifying the LT-FH method to incorporate age information as a function of the liability threshold model parameter for age for 12 UK Biobank diseases.
We plot the increase in number of independent loci for \({\mathrm{LT}}{\hbox{-}}{\mathrm{FH}}_{no{\hbox{-}}sib,age}^{PA}\) relative to for \({\mathrm{LT}}{\hbox{-}}{\mathrm{FH}}_{no {\hbox{-}} sib}^{PA}\) (Supplementary Table 32) against the liability threshold model parameter |cage|(Supplementary Table 30).
Extended Data Fig. 4 LT-FH increases association power across 12 diseases from the UK Biobank in analyses incorporating related individuals.
We report results of GWAS using BOLT-LMM on related Europeans, GWAX using BOLT-LMM on unrelated Europeans, and LT-FH using BOLT-LMM on related Europeans using only case–control status for all sibling pairs and parent-offspring pairs within the set of target samples. Numerical results are reported in Supplementary Table 37.
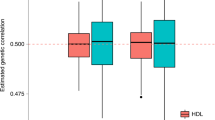
Extended Data Fig. 5 Strong concordance between GWAS BOLT-LMM-inf effect sizes and transformed LT-FH BOLT-LMM-inf effect sizes.
We plot GWAS BOLT-LMM-inf effect sizes and transformed LT-FH BOLT-LMM-inf effect sizes for genome-wide significant effect sizes (P≤5*10−8 for both GWAS and LT-FH BOLT-LMM-inf). We note that BOLT-LMM only outputs effect size estimates for BOLT-LMM-inf, the BOLT-LMM approximation to the infinitesimal mixed model. Our effect size for GWAS is the outputted βGWAS,BOLT−LMM−inf (per-allele observed scale) and for LT-FH we estimate a (per-allele observed scale) effect size as \(\begin{array}{l}\beta = \frac{{\beta _{LT - FH,BOLT - LMM - inf}}}{{se\left( {\beta _{LT - FH,BOLT - LMM - inf}} \right)\sqrt {N_{GWAS} \ast c} }} \frac{{\sqrt {K(1 - K)} }}{{\sqrt {2\left( {MAF} \right)\left( {1 - MAF} \right)} }}\end{array}\), where c is the boost in Neff for LT-FH relative to GWAS, K is disease prevalence in GWAS and MAF is the minor allele frequency of the SNP.
Supplementary information
Supplementary Information
Supplementary Note and Supplementary Tables 1–45
Rights and permissions
About this article
Cite this article
Hujoel, M.L.A., Gazal, S., Loh, PR. et al. Liability threshold modeling of case–control status and family history of disease increases association power. Nat Genet 52, 541–547 (2020). https://doi.org/10.1038/s41588-020-0613-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41588-020-0613-6