Abstract
The interplay of charge, spin, lattice and orbital degrees of freedom leads to a variety of emergent phenomena in strongly correlated systems. In transition-metal-dichalcogenide-based moiré heterostructures, recent observations of correlated phases can be described by triangular-lattice single-orbital Hubbard models based on moiré bands derived from the Brillouin-zone corners—the so-called K valleys. Richer phase diagrams described by multi-orbital Hubbard models are possible with hexagonal lattices that host moiré bands at the zone centre—called Γ valleys—or an additional layer degree of freedom. Here we report the tunable interaction between strongly correlated hole states hosted by Γ- and K-derived bands in a heterostructure of monolayer MoSe2 and bilayer 2H WSe2. We characterize the behaviour of exciton–polarons to distinguish the layer and valley degrees of freedom. The Γ band gives rise to a charge-transfer insulator described by a two-orbital Hubbard model. An out-of-plane electric field re-orders the Γ- and K-derived bands and drives the redistribution of carriers to the layer-polarized K orbital, generating Wigner crystals and Mott insulating states. Finally, we obtain degeneracy of the Γ and K orbitals at the Fermi level and observe interacting correlated states with phase transitions dependent on the doping density. Our results establish a platform to investigate multi-orbital Hubbard model Hamiltonians.
Similar content being viewed by others
Main
Although conceptually simple, the single-orbital two-dimensional Hubbard model can describe many ingredients of strongly correlated systems. However, real quantum materials are typically described using multi-orbital Hubbard models. For instance, doping in the two-orbital charge-transfer insulator has been connected to high-temperature superconductivity in cuprates1,2,3 and iron-based superconductors demand Hubbard models that account for multiple degenerate orbitals at the Fermi level4. Although challenges exist to accurately solve the single-orbital Hubbard model and its derivatives, the phase diagrams of more complex multi-orbital models become even more intractable; they sensitively depend on the interplay of the different degrees of freedom5. Hence, there is a strong motivation to develop platforms for strongly correlated physics that are relatively simple yet possess a high degree of tunability such that emergent physics can be probed and accurately mapped onto paradigmatic quantum Hamiltonians6,7.
Synthetic moiré superlattices, formed by stacking two atomic layers with a lattice mismatch or a relative twist angle, have emerged as a versatile solid-state platform that potentially fulfils these criteria7,8. The versatility of moiré materials arises from the impressive array of tuning knobs that can effectively control the moiré lattice and adjust the strength and nature of the particle interactions. For instance, electrostatic gating can fine-tune the fractional filling (ν) of the lattice with carriers (for electrons or holes, namely, νe or νh, respectively), displacement fields can adjust the moiré potential depth9,10 and long-range Coulomb interactions can be manipulated with screening gates11,12. Further, in semiconducting transition metal dichalcogenide (TMD)-based moiré systems, the strengths of Coulomb interactions between particles in the moiré lattice can be continuously tuned via the moiré period13,14. Additionally, different real-space lattice geometries can be found in the low-energy valence moiré bands, dependent on the valley degree of freedom: moiré orbitals on a triangular lattice are generally found for K-valley moiré bands localized on a single atomic layer13,14,15,16,17,18,19, whereas honeycomb lattices are found for Γ-valley moiré bands spread across each layer20,21,22,23,24,25,26,27. In particular, the energetic ordering of Γ- versus K-derived valence moiré bands is sensitively dependent on material combination, twist angle and atomic relaxation effects28. To date, most experimental observations of correlated states in both TMD moiré homo- and heterobilayers have been sufficiently described by single-band Hubbard models. Thus, experimentally realizing tunable moiré systems that portray multi-orbital Hubbard physics remains an exciting opportunity in this emerging platform.
Here, by stacking a natural bilayer (2L) of 2H WSe2 on monolayer (1L) MoSe2 with a relative twist angle to create a heterotrilayer (HTL) device with only one moiré interface, we demonstrate a degree of freedom to realize an extended t–U–\({{{V}}}\) three-orbital Hubbard system based on low-energy moiré bands at Γ and K, which host distinct real-space lattice geometries. Crucially, the relative ordering of these bands can be fine-tuned with an external electric (displacement) field \(\overrightarrow{E}\) and we are able to investigate the interplay of correlated states between different orbitals. To precisely probe the nature of the correlated states, we develop an optical spectroscopy technique based on the distinctive behaviour of exciton–polarons29 that unambiguously distinguishes the layer and valley degrees of freedom (Methods).
Layer and valley degrees of freedom for holes in moiré bands
Our HTL sample is a natural 2L of 2H WSe2/1L MoSe2 device with a moiré interface period of approximately 7 nm due to a relative twist angle of θ ≈ 2.7 ± 0.5° with respect to R stacking. Compared with a 1L WSe2/1L MoSe2 HBL device, the HTL provides an additional layer degree of freedom17,19,30, as well as raising the prospect for exploitation of the valley degree of freedom in the valence band31. To aid an unambiguous identification of the spectral features in the HTL device, we investigate a sample (Fig. 1d shows the device schematic) with adjacent HBL and HTL regions with nominally identical moiré period at each WSe2/MoSe2 interface (Methods). Hence, the HBL serves as a reference with well-understood exciton–polaron behaviour in the presence of strongly correlated states18.
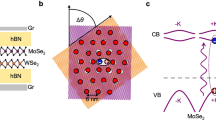
a,b, Density plots of the Vg dependence of d(ΔR/R0)/dE in the 1L WSe2/1L MoSe2 (HBL) (a) and 2L WSe2/1L MoSe2 (HTL) (b) heterostructure regions. The MoSe2 moiré excitons, namely, MXMo,1 and MXMo,2, and WSe2 neutral excitons, namely, X\({}_{{{{\rm{W}}}}}^{0}\), are indicated. In the HTL, intralayer excitons localized in the interface (L1) and upper (L2) layers of 2L WSe2 are non-degenerate due to different dielectric environments (ϵ), as indicated in d. The white dashed lines indicate integer values of electrons and holes per moiré unit cell, that is, νe and νh, respectively. d, Schematic of the full device with HBL and HTL regions. The TMD layers are fully encapsulated in hBN. Graphene (Gr) layers form contacts to the top and bottom hBN and the heterostructure. c,e, Schematic of the band structure for the moiré Brillouin zone based on the DFT calculations in the HBL (c) and HTL (e) regions. In the HBL region, optically injected excitons reside in ±K-derived states and are solely dressed by holes in the ±K moiré orbitals. In the HTL region, the excitons are dressed by holes at both Γ and ±K moiré bands. As indicated in the insets, the Γ moiré orbitals form a honeycomb lattice with inequivalent A and B sites. The moiré orbitals from the ±K valleys form a triangular lattice.
Figure 1a,b shows doping (Vg)-dependent sweeps (Methods) and monitoring the derivative of the reflection contrast with respect to energy (d(ΔR/R0)/dE) in the representative HBL and HTL regions of the device, respectively, at a temperature of 4 K. We observe doping-dependent periodic modulations in the peak position, intensity and linewidth of all the intralayer excitonic features at Vg values corresponding to integer ν (Fig. 1a,b, white dashed lines), indicating the formation of correlated electron and hole states. In contrast to the HBL region, in the HTL, we observe two WSe2 intralayer exciton peaks with different transition energies due to their different dielectric environments (Fig. 1d). The lower-energy feature, labelled X\({}_{{{{\rm{W,L1}}}}}^{0}\), is the WSe2 neutral exciton localized in the heterostructure interface layer (L1), whereas the higher-energy exciton, that is, X\({}_{{{{\rm{W,L2}}}}}^{0}\), is localized in the top layer (L2) (Methods). This spectroscopic signature provides a clear probe to determine which WSe2 layer is occupied by the Fermi sea under doping (via the formation of attractive exciton–polarons for each intralayer exciton). The type-II band alignment formed at the interface between L1 WSe2 and MoSe2 leads to fast non-radiative dephasing and a larger linewidth for X\({}_{{{{\rm{W,L1}}}}}^{0}\) compared with X\({}_{{{{\rm{W,L2}}}}}^{0}\) (ref. 32). Although all data are measured on a single device, we measure multiple spatial locations in the HTL region and find that the behaviour shown here is general (Extended Data Fig. 1 and Extended Data Table 1).
Figure 1c,e shows the schematic of the valence band in the moiré Brillouin zone for HBL and HTL, respectively, based on calculations using ab initio density functional theory (DFT) (Supplementary Discussion 4). Moiré bands derive from either states near the Γ or ±K points. Doped carriers that occupy the valence moiré band arising from ±K form a two-dimensional triangular lattice. In contrast, the holes in the moiré band derived from Γ form a honeycomb lattice with inequivalent A and B sites (Fig. 1e). In addition, the moiré bands inherit the contrasting properties of the different Brillouin-zone locations. Holes in the K-derived bands are highly localized in one of the WSe2 layers, as shown by the layer distribution of the hole wavefunction (Supplementary Fig. 8), whereas Γ holes are delocalized across both the WSe2 layers. The ΓA band is the lowest-energy-available valence moiré band. In each sample, optically excited electron–hole pairs reside in ±K-derived bands, whereas carriers that dress the excitons are doped into the lowest-energy-available valence band, which can be derived from either ±K or Γ. According to the selection rules, for the HTL, σ+ (σ−) light probes the +K-derived (−K-derived) states in L1 and the −K-derived (+K-derived) states in L2 of the natural 2L WSe2, due to 2H stacking and spin-layer locking33,34.
Probing Γ-valley correlated electronic states
Figure 2a,b shows the σ+- and σ−-resolved νh dependence of the d(ΔR/R0)/dE signal, respectively, in the HTL under a 5 T magnetic (B) field. The solid lines indicate integer values of νh (that is, the total number of holes per moiré unit cell). To further highlight the formation of correlated electronic states, we plot the derivative of the reflection contrast with respect to Vg, that is, d(ΔR/R0)/dVg (Fig. 2c,d). We note the largest changes in d(ΔR/R0)/dVg (at Vg values of −1.1, −2.1 and −3.1 V) identify the formation of different insulating correlated hole states (νh = 1, 2 and 3, respectively). There is a small charge-neutrality region (Extended Data Fig. 6). The Vg value required to fill the moiré lattice with either one electron or one hole per site is identical and corresponds to a twist angle of 2.7° (Methods). We perform temperature-dependent sweeps of Vg and monitor ΔR/R0 and find a critical temperature Tc ≈ 98 K for the correlated state at νh = 1 and Tc ≈ 59 K for the correlated state at νh = 2 (Extended Data Figs. 4 and 5). We also observe changes in d(ΔR/R0)/dVg at further intermediate hole fillings (Fig. 2c,d, black dashed lines), which we ascribe to the formation of generalized Wigner crystals that arise due to long-range Coulomb interactions16,30,35. Although an in-depth understanding about the specific charge and spin ordering of these states is beyond the scope of this work, we refer to recent theoretical works as a starting point to address these issues22,36,37,38.
a,b, σ+-helicity-resolved (a) and σ−-helicity-resolved (b) evolution of d(ΔR/R0)/dE, as a function of νh under an applied magnetic field of 5 T. c,d, Density plot of the first derivative with respect to the gate voltage of ΔR/R0 (d(ΔR/R0)/dVg) in a (c) and b (d). The orbital at the Fermi level is depicted in the schematic to the right. On all the plots, the solid lines indicate integer νh, whereas the dashed and dotted lines in c and d show intermediate fractional fillings.
We observe that there is little change in the two WSe2 excitonic resonance energies as hole doping increases from zero to νh = 1. After νh = 1, X\({}_{{{{\rm{W,L1}}}}}^{0}\) and X\({}_{{{{\rm{W,L2}}}}}^{0}\) abruptly redshift, indicating the formation of the hole-dressed attractive polarons AP\({}_{{{{\rm{W,L1}}}}}^{+}\) and AP\({}_{{\rm{W,L2}}}^{+}\) (ref. 39). Three key signatures indicate that the valence-band maximum in the system derives from the Γ valley, as predicted by the DFT calculations (Fig. 1e). First, AP\({}_{{{{\rm{W,L1}}}}}^{+}\) and AP\({}_{{{{\rm{W,L2}}}}}^{+}\) redshift with increasing νh. This is in contrast to natural 2L 2H WSe2, where an overall blueshift in AP\({}_{{\rm{W}}}^{+}\) occurs due to Pauli blocking effects: resident carriers fill up the states at the valence band at the ±K point where the photoexcited hole also resides40 (Supplementary Discussion 2). The contrasting redshift in the moiré HTL implies that the valence-band maximum is not derived from the ±K states. Second, unlike the examples of strong spin polarization of holes residing in ±K valleys29, in Fig. 2a,b, we observe negligible differences in the intensity and energy of AP\({}_{{{{\rm{W,L1}}}}}^{+}\) and AP\({}_{{{{\rm{W,L2}}}}}^{+}\) between the σ+- and σ−-resolved sweeps at B = 5 T, indicating an absence of spin polarization for the doped holes. This finding is consistent with a photoexcited exciton that resides at ±K dressed by doped holes in moiré bands derived from the Γ point. Finally, AP\({}_{{{{\rm{W,L1}}}}}^{+}\) and AP\({}_{{{{\rm{W,L2}}}}}^{+}\) forming at an identical Vg value is further evidence: holes in the Γ band are delocalized across the two WSe2 layers and equally dress both X\({}_{{{{\rm{W,L1}}}}}^{0}\) and X\({}_{{{{\rm{W,L2}}}}}^{0}\). In the absence of the delocalization of holes, we would expect carriers to sequentially fill the L1- and L2-derived moiré bands, causing a Vg offset in the formation of AP\({}_{{{{\rm{W,L1}}}}}^{+}\) and AP\({}_{{{{\rm{W,L2}}}}}^{+}\).
We now discuss the nature of the correlated state that arises at νh = 1 in the Γ orbital, which is determined to be a charge-transfer insulator. The energy gap between the two Γ moiré bands that map onto inequivalent A and B sites of a honeycomb lattice (ΓA and ΓB orbitals, respectively) is predicted by DFT to be approximately 18 meV (Supplementary Discussion 4), comparable with the value of the charge gap we can tentatively estimate from the temperature at which the correlated state at νh = 1 disappears, which is approximately 10 meV (Extended Data Fig. 5). Therefore, the ΓA lattice is first completely filled, followed by the sequential filling of the ΓB sites. The inequivalency of the A–B sublattice also presents a probable explanation for the lack of formation of AP\({}_{{{{\rm{W,L1}}}}}^{+}\) and AP\({}_{{{{\rm{W,L2}}}}}^{+}\) up to νh = 1. The DFT calculations reveal that the photoexcited hole at K resides on the site of B sublattice, whereas for 0 < νh < 1, the doped hole in the Γ moiré band lies on the A site (Supplementary Fig. 8). Hence, there is no spatial or momentum overlap between the two states, minimizing the formation of an attractive exciton–polaron41. For 1 < νh < 2, holes are doped into the ΓB moiré orbital, which spatially overlaps with the photoexcited hole. Hence, attractive polarons form in each layer for this range of νh.
Electric-field tuning of moiré orbitals
We now investigate the field tunability of the bands. By probing the magneto-optical properties of WSe2 exciton–polarons, we disentangle the different spin and valley properties of the holes doped into the Γ and ±K moiré bands as a function of \(\overrightarrow{E}\), using the tuning knob VE (Methods provides the definition of VE). Figure 3a,b shows the polarization-resolved d(ΔR/R0)/dE sweeps as a function of νh with B = 5 T and VE = +3 V. As we increase νh in the σ−-resolved spectrum (Fig. 3b), a new resonance (labelled AP\({}_{{{{\rm{W,L2}}}}}^{+}\), indicated by the red arrow) appears at νh = 1, ~14 meV lower energy than X\({}_{{{{\rm{W,L2}}}}}^{0}\). This resonance is particularly absent for the σ+ spectrum (Fig. 3a), where, instead, X\({}_{{{{\rm{W,L2}}}}}^{0}\) evolves into the repulsive-polaron branch RP\({}_{{{{\rm{W,L2}}}}}^{+}\) that blueshifts with increasing doping. The difference in oscillator strengths for RP\({\rm{{}_{W,L2}^{+}}}\) and AP\({\rm{{}_{W,L2}^{+}}}\) in the σ+- and σ−-polarized Vg sweeps indicates a large degree of spin polarization for the carriers that form the exciton–polarons in L2. We, therefore, unambiguously identify AP\({}_{{{{\rm{W,L2}}}}}^{+}\) as the intervalley attractive polaron, which is formed from the direct ±K exciton in L2 dressed with holes in the opposite K valley in L2 (ref. 29). This observation strongly indicates that at VE = +3 V, the L2 K-derived band is tuned upwards in energy relative to the layer-hybridized ΓB band. Previously, for VE = 0 V and holes loaded only at Γ, there is a complete lack of hole spin polarization, regardless of νh (Fig. 2a,b).
a,b, νh dependence of the σ+-resolved (a) and σ+-resolved (b) d(ΔR/R0)/dE at VE = +3 V with B = 5 T. c,d, Density plot of d(ΔR/R0)/dVg in a (c) and b (d), which highlight the formation of correlated states (identified by the dashed and solid lines). The orbital at the Fermi level is depicted in the schematic on the right. e,f, σ+-resolved (e) and σ−-resolved (f) B-field sweep of d(ΔR/R0)/dE at VE = +3 V and νh = 2. The red dots represent the B-field-dependent estimated energies of AP\({}_{{{{\rm{W,L2}}}}}^{+}\). g, B-field-dependent Zeeman splitting ΔE of AP\({}_{{\rm{W}}}^{+}\) at representative hole values of νh = 2 for VE = 0 V (black dots) and VE = +3 V (red dots). For VE = +3 V, ΔE is extracted from the estimated positions shown in e and f. The g-factor of AP\({}_{{{{\rm{W,L2}}}}}^{+}\) is extracted from linear fits to ΔE (solid lines). The calculated errors represent one standard deviation.
Next, we investigate the interaction effects on the magneto-optics for the correlated states in the Γ and K orbitals. Figure 3e,f shows the helicity-resolved evolution of the d(ΔR/R0)/dE spectra for applied B fields between −5 and +5 T at νh = 2 and VE = +3 V. The B-field-dependent estimated energy of AP\({}_{{{{\rm{W,L2}}}}}^{+}\) extracted from the fits are overlaid in this figure (red dots). Figure 3g shows the Zeeman splitting ΔE of AP\({}_{{{{\rm{W,L2}}}}}^{+}\) versus the B field at νh = 2, for both VE = 0 V (black) and VE = +3 V (red), where \({{\Delta }}E={E}^{{\sigma }^{+}}-{E}^{{\sigma }^{-}}\) (\({E}^{{\sigma }^{\pm }}\), transition energy with σ± polarization). The evolution of ΔE with B field can be associated with an effective exciton g-factor using ΔE(B) = gμ0B, where μ0 is the Bohr magneton. For VE = 0 V, when AP\({}_{{{{\rm{W,L2}}}}}^{+}\) is formed by an exciton dressed by holes at Γ, the g-factor is close to –4, which is expected according to spin and valley considerations in the absence of interaction effects29. In contrast, for VE = +3 V, AP\({}_{{{{\rm{W,L2}}}}}^{+}\) exhibits a large positive g-factor of approximately 49, partly due to interaction effects that arise from hole doping into the ±K band and the resulting favoured single-valley occupancy (Extended Data Fig. 3 and Extended Data Table 2)29. The measured g-factor is then further enhanced by spin coupling between the moiré localized holes15,18.
The tuning of the valence bands in the system is further demonstrated by the suppression of the formation of the attractive polaron for the L1 WSe2 exciton, that is, AP\({}_{{{{\rm{L1}}}}}^{+}\), up to νh > 2: holes are doped into the highly localized L2 K band and therefore have little effect on the L1 WSe2 exciton. Finally, we note that the binding energy EB for the hole-dressed attractive polaron formed by the L2-localized exciton for VE = +3 V (EB ≈ 14 meV) is much larger than the binding energy for VE = 0 V (EB ≈ 6 meV). This result is consistent with a larger wavefunction overlap between the exciton at ±K dressed by holes at ∓K compared with holes at Γ.
Correlated states: Γ versus K orbitals
We now investigate the correlated states formed within the Γ and K orbitals. We expect the same dependence of Vg versus νh for each orbital. Figure 3c,d shows the νh dependence of d(ΔR/R0)/dVg for the same data in Fig. 3a,b, respectively. As expected, we observe the largest changes in the d(ΔR/R0)/dVg signal at integer νh and smaller changes at intermediate νh, as previously observed for VE = 0 V (Fig. 2c,d). However, we observe that new correlated states emerge for VE = +3 V compared with VE = 0 V. A new state at νh = 4 clearly appears, as well as further states at νh = 7/3 and 8/3.
To understand the origin of the additional correlated insulating states, we again use the polarization-resolved doping-dependent reflection contrast measurements (Figs. 2a,b and 3a,b) and assign the correlated states to filling of either the Γ or K orbitals, as indicated by the schematics on the far right in these figures. For νh < 1, we observe that attractive polarons do not form for any VE because holes are always doped first into the ΓA orbital. We then observe that AP\({}_{{{{\rm{W,L2}}}}}^{+}\) and RP\({}_{{{{\rm{W,L2}}}}}^{+}\) form at νh > 1 with a large spin polarization, demonstrating doping into the K orbital. Hence, for VE = +3 V at νh = 2, a correlated state arises in which the lower Hubbard bands are filled for both ΓA and K orbitals. In contrast, for VE = 0 V and 1 < νh < 2, the ΓB orbital is filled, as demonstrated by the lack of spin polarization of the carriers that form AP\({}_{{{{\rm{W,L1}}}}}^{+}\) and AP\({}_{{{{\rm{W,L2}}}}}^{+}\) (Fig. 2a,b).
Continuing with the VE = +3 V scenario, after νh = 2, the non-spin-polarized AP\({}_{{{{\rm{W,L1}}}}}^{+}\) forms because holes are now doped into the ΓB orbital. Hence, at νh = 3, a correlated state arises in which each orbital (ΓA, ΓB and K) is filled with one hole. Finally, for νh > 3, AP\({}_{{{{\rm{W,L2}}}}}^{+}\) continually blueshifts with increasing doping, indicating Pauli blocking effects arising from doping into the K orbital, whereas AP\({}_{{{{\rm{W,L1}}}}}^{+}\) remains unaffected. At νh = 4, we, therefore, have a correlated state with νΓ = 2 and νK = 2. These assignments are consistent with the emergence of new states at νh = 7/3 and 8/3 for VE = +3 V. In comparison, for VE = 0 V, the Wigner crystals driven by long-range interactions are not observed at these νh values in the next Γ moiré orbital. The emergence of new correlated states at νh = 7/3, 8/3 and 4 is consistent with metal–insulator transitions occurring at these νh values, driven by VE-dependent tuning of the relative Γ–K-band energies.
Interplay of correlated states between degenerate orbitals
To better understand the VE-dependent shifts in the K and ΓB orbitals, we perform DFT calculations for the HTL in the presence of a vertical electric field. Figure 4a shows a simplified schematic of the band structure in the moiré Brillouin zone for a positive vertical electric field (Supplementary Discussion 4 shows the calculated full band structure). In agreement with the experiment, we observe that the ±K-derived bands localized on L2 are pushed up in energy (that is, reduced hole energy) relative to the ΓB bands (Fig. 1e shows a comparison). Figure 4b shows the band-edge energy of the ΓA, ΓB, L1 K and L2 K bands as function of the applied electric-field strength. Due to the high localization of its wavefunction on L2 WSe2 (Supplementary Fig. 7), the L2 K orbital exhibits the largest VE-dependent shift in energy. In contrast, the ΓA and ΓB bands exhibit smaller VE-dependent energy shifts due to delocalization across both WSe2 layers31.
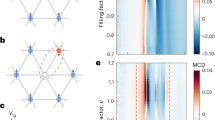
a, Schematic of the band structure for the moiré Brillouin zone based on DFT calculations of the HTL under an applied positive vertical electric (E) field. The K-derived band is shifted to a higher energy relative to the Γ-derived bands compared with VE = 0. b, Electric-field dependence of the valence-band maximum for the Γ- and K-derived moiré bands, calculated from DFT. c, Density plot of the VE dependence of the derivative of the d(ΔR/R0)/dE when hole filling is fixed at νh = 2. The white dashed line indicates an abrupt transfer of holes in the system from the Γ-derived moiré orbital to the K-derived orbital. d,e, νh dependence of the σ+-resolved (d) and σ−-resolved (e) d(ΔR/R0)/dE at VE = +2 V and B = 5 T. f,g, Density plot of d(ΔR/R0)/dVg for the same data in d (f) and e (g), respectively. On all the plots, the solid lines indicate integer νh of the moiré superlattice, whereas the dashed and dotted lines in f and g show intermediate fractional fillings. The schematic on the far right indicates the carriers per moiré unit cell in each of the Γ- or K-derived orbitals, where a filled circle indicates integer filling.
To probe the interplay between correlated states in Γ and K orbitals in more detail, we measure the VE dependence of the d(ΔR/R0)/dE signal for a fixed hole filling of νh = 2 (Fig. 4c). For VE = 0 V, we observe the two WSe2 attractive polaron resonances: intralayer excitons localized in L1 and L2 of the bilayer dressed by delocalized holes residing in the highest Γ moiré miniband (AP\({}_{{{{\rm{W,L1}}}}}^{+}\) and AP\({}_{{{{\rm{W,L2}}}}}^{+}\), respectively). However, as VE increases, these features are abruptly replaced by three new resonances at VE ≈ 2.3 V. The full-width at half-maximum of the change in the d(ΔR/R0)/dE signal is calculated to be ΔVE = 0.53 V (Extended Data Fig. 2). To identify the origin of the abrupt change, we measure the helicity-resolved νh dependence of d(ΔR/R0)/dE with VE = +2 V and B = 5 T (Fig. 4d,e). Figure 4f,g shows the νh dependence of d(ΔR/R0)/dVg for the same data. Identical to the case for VE = +3 V, in the σ− spectrum (Fig. 4d), we observe the emergence of a new highly spin-polarized resonance AP\({}_{{{{\rm{W,L2}}}}}^{+}\) (red arrow), indicating that holes are initially doped into the L2 K moiré band for νh > 1. However, for σ−, at around νh = 2, the oscillator strength is transferred to a higher-energy feature with a smaller binding energy, which also appears for the σ+-resolved data (Fig. 4d, blue arrows). This feature lacks a strong degree of spin polarization, suggesting that holes are transferred from the K to the ΓB orbital at νh = 2. The hole transfer is further demonstrated by the formation of an attractive polaron for the L1 WSe2 exciton at around νh = 2, at the same hole filling where the transfer of oscillator strength occurs. For νh > 2, holes start to be doped into the K orbital again, and the spin-polarized features re-emerge. Therefore, we assign the abrupt change in the absorption spectrum at VE = +2.3 V (Fig. 4c) to a transfer of holes from the ΓB to the K moiré orbital.
Rather than being continuous, the observed change occurs over a small range of VE (ΔVE ≈ 0.5 V). If holes were continuously transferred between the orbitals, there would be a gradual change in oscillator strength17. Instead, the abrupt change indicates that the system favours the formation of a correlated state, and the different VE-dependent scenarios for νh = 2 provide an archetypal illustration. For a small VE, a correlated state with νh = 1 in each ΓA and ΓB orbit arises. For large VE, a correlated state with νh = 1 in the ΓA orbital and νh = 1 in the K orbital is formed. However, when the ΓB and K orbitals are nearly degenerate at the Fermi level, the holes preferentially transfer from the K orbital to the ΓB orbital, probably due to a larger Coulomb gap for the filled ΓB orbital, which minimizes the energy of the correlated state. A summary of the orbital filling near degeneracy is depicted as a schematic (Fig. 4g, right).
Discussion
In the experiment, we observe an interplay between correlated states in three orbitals, which can be tuned with VE. Here we apply a t–U–\({{{{V}}}}\) Hamiltonian in the t/U → 0 limit (Methods) to provide a more detailed picture of the charge ordering and interactions of these correlated states. Charges can be distributed (and redistributed) between the ΓA, ΓB and K orbitals as hole filling increases. It is probable that complex correlated states with specific charge ordering in real space arise to minimize electrostatic repulsion for a given νh, similar to that observed in bilayer Hubbard model physics19.
First, we model the trilayer with VE = 0, where the onsite energy for the L2 K orbital (εK) is much larger than both ΓA and ΓB onsite orbital energies (εA and εB, respectively). For νh = 1, the holes occupy the ΓA orbitals, forming a triangular lattice (Fig. 5a). This correlated state is characterized by an occupied lower hole Hubbard band, which is separated from the upper hole Hubbard band by the onsite Coulomb energy \({U}_{{{{\Gamma }}}_{{\rm{A}}}}\) (Fig. 5a). Further hole doping results in the occupancy of the ΓB sites as well as the formation of charge-ordered ΓB states, consistent with the experimental findings of the Γ-derived Wigner crystal at νh = 4/3 (Fig. 2c,d). At νh = 2, all the ΓA and ΓB sites are occupied, whereas the L2 K orbital remains empty.
a, Charge-ordered states (formulated using Monte Carlo simulations) that arise in the Γ (pink and purple) and K (red) moiré lattices for VE = 0, for which the energy of the K-derived band is below both Γ-derived bands (ϵK < ϵB). The ΓB sites are spatially aligned with the K sites in the x–y plane. Holes are first loaded into the ΓA sites up to νh = 1 and into the ΓB sites for νh > 1. Schematic to the right illustrates the hole energy versus density of states (DOS) for each charge-ordered state shown in these data. The lower Hubbard band (LHB) and upper Hubbard band (UHB) form for νh = 1, whereas a charge gap Δ opens up for correlated states that form for non-integer filling. b, Charge-ordered states (formulated using Monte Carlo simulations) and the corresponding DOS schematic that arises for VE = +3 V, for which the energy of the K orbital lies between the Γ orbitals (ϵA > ϵK > ϵB). Holes are first loaded into the ΓA sites up to νh = 1 and into K for νh > 1. c, Experimentally observed charge-ordered states and corresponding DOS schematics for VE = +2.3 V for which the K orbital is energetically degenerate with the ΓB orbital. Holes are first loaded into the ΓA sites up to νh = 1, and into both K and ΓB for νh > 1. At νh = 2, holes are abruptly transferred from K to ΓB to form the correlated state with νΓA = 1 and νΓB = 1.
Next, we consider the case of a large electric field, namely, VE = +3 V, with εB > εK > εA and for νh = 1, the holes still occupy the ΓA sites. Further hole doping, however, results in the L2 K orbital becoming occupied and forming charge-ordered states (Fig. 5b), consistent with the experimental picture of B-field-dependent correlated states at νh = 4/3. At νh = 2, the lower Hubbard bands of the ΓA and L2 K orbitals are fully occupied by holes, whereas the upper Hubbard bands are empty.
Finally, we consider the critical electric field, namely, VE = +2.3 V. At this field, εB ≈ εK > εA and we expect strong quantum interaction effects to occur, which are not captured by our electrostatic model. For νh = 1, the holes still occupy the ΓA sites. As a result of the degeneracy of the ΓB and L2 K orbitals, we hypothesize that additional holes (1 < νh < 2) occupy both orbitals to minimize the overall Coulomb repulsion (Fig. 5c). When the doping reaches νh = 2, we experimentally observe that all the holes reside in Γ-derived states. This can be explained by the formation of a correlated state in which the lower Hubbard bands for both ΓA and ΓB orbitals are fully occupied. As the bandwidth of the Γ-derived bands is smaller than that of the K-derived bands (according to DFT calculations), it is energetically favourable for the Γ orbitals to be fully occupied. Thus, the holes spontaneously redistribute from the K to ΓB orbital. This observation provides motivation for future theoretical and experimental investigations to fully understand the many-body physics of this strongly correlated multi-orbital system.
Methods
Exciton–polaron spectroscopy of correlated states with layer and valley specificity
To precisely probe the nature of the correlated states, we develop an optical spectroscopy technique that yields unambiguous layer- and valley-specific experimental signatures. We probe momentum-direct electrons and holes at ±K valleys that form tightly bound intralayer excitons, which are extremely sensitive to their environment. The binding energy of the exciton depends on its dielectric environment42, leading to layer-specific exciton energies43, whereas excitons dressed by a Fermi sea form attractive exciton–polarons (AP) and repulsive exciton–polarons (RP)44,45, which exhibit distinct behaviours depending on the valley hosting the Fermi sea. For doping at ±K, dominant phase-space-filling effects cause an overall blueshift in the AP29, whereas doping in the Γ valley leads to a continuous redshift due to bandgap renormalization46. Contrasting properties in an applied magnetic field also manifest for excitons dressed by carriers in the two valleys: unlike Γ-valley holes, K-valley holes are highly spin polarized and exhibit strong magnetic interactions with excitons at ±K (ref. 29). Finally, the formation of strongly correlated states leads to abrupt changes in the oscillator strength, energy and linewidth of the exciton–polarons, regardless of which valley the Fermi sea occupies15,17,18. Altogether, exciton–polarons provide probes of strongly correlated electronic states with layer and valley specificity.
Device details
The moiré region in the heterostructure is fully encapsulated in hexagonal boron nitride (hBN). There are few-layer graphene contacts to both top and bottom hBN, as well as the heterostructure that allows the carrier concentration and vertical electric field to be independently tuned (Fig. 1b). To change the carrier concentration in the heterostructure without changing the vertical electric field, we sweep both VT and VB with the same values, that is, VT = VB = ΔVg. To change the vertical electric field without changing the carrier concentration, VT = −VB = VE. The applied vertical electric field can then be calculated using \(E=\frac{({V}_{{\rm{T}}}-{V}_{{{{\rm{B}}}}})}{({d}_{1}+{d}_{2})}\frac{{\epsilon }_{{\rm{hBN}}}}{{\epsilon }_{{\rm{TMD}}}}\). For intermediate regimes, when we want to change both applied vertical electric field and carrier concentration, we apply asymmetric gating, that is, VT ≠ VB.
To experimentally calibrate νh, we identify the first three largest changes in the d(ΔR/R0)/dVg signal. We find that for each applied VE, the dashed lines are equidistant in ΔVg. Hence, we assign them to be νh = 1, 2 and 3. We observe that the calibrated values exhibit a slight Vg offset from Vg = 0 V for the charge-neutrality region (νh = 0) in the device, and the Vg offset becomes larger for increasing VE. The carrier concentration n in the heterostructure can be calculated using the parallel-plate capacitor model, that is, \(n=\frac{\epsilon {\epsilon }_{0}{{\Delta }}{V}_{{{{\rm{g}}}}}}{{d}_{1}}+\frac{\epsilon {\epsilon }_{0}{{\Delta }}{V}_{{{{\rm{g}}}}}}{{d}_{2}}\), where ϵ is the permittivity of hBN, ΔVg is the voltage offset between both top and bottom gates and heterostructure gate and d1 (d2) is the thickness of the top (bottom) hBN layer and measured to be 17.4 ± 0.2 nm (18.2 ± 0.3 nm) using nulling ellipsometry. For a small angular difference between two stacked layers, the moiré periodicity can be estimated using \({\lambda }_{{\rm{M}}}=\frac{{a}_{{\rm{Se}}}}{\sqrt{{\delta }^{2}+{\theta }^{2}}}\), where aSe is the lattice constant of WSe2, δ is the fractional lattice mismatch between the two layers and θ is the twist angle in radians. For a triangular moiré pattern (or honeycomb with inequivalent A and B sites, where only one site is doped), the number of carriers required for one hole per site is given by \({n}_{0}=\frac{2}{\sqrt{3}{\lambda }_{{\rm{M}}}^{2}}\). Using the lattice constants of 0.3280 and 0.3288 nm for WSe2 and MoSe2, respectively47; permittivity of 3.8 for hBN (ref. 48); and ΔVg = 1.00 V for νh = 1 (as determined in the main text), we calculate the twist angle in the main measurement location to be 2.7°. We determine that the interface in HTL is R stacked as a result of the fabrication process. Single flakes of MoSe2 and WSe2 with monolayer and natural 2H bilayer regions are first exfoliated with the terraced layers (flat surface) facing up (on the substrate). The WSe2 flake (terraced side up) is then transferred onto MoSe2 on its substrate, keeping the interface between the two layers free from contaminants. The HBL region is H stacked, as demonstrated by magneto-optical studies on the same sample49,50 and polarization-resolved second-harmonic generation measurements (Supplementary Discussion 1), whereas in the HTL region, the WSe2 interface layer L1 is R stacked relative to 1L MoSe2. The upper WSe2 layer L2 is, therefore, H stacked relative to 1L MoSe2. We note that second-harmonic generation measurements cannot be used to determine R versus H stacking of the HTL heterointerface. DFT calculations show that both R- and H-stacked interfaces lead to qualitatively identical band structures with ground-state Γ-derived moiré bands with a honeycomb lattice (Extended Data Fig. 7).
Optical spectroscopy measurements
We focus a broadband white-light source from a power-stabilized halogen lamp onto the sample, and measure the reflected signal in a liquid-nitrogen-cooled charge-coupled device spectrometer. The sample is mounted in a closed-cycle cryostat and the sample temperature for all the experiments in the main text is 4 K. We define the reflection contrast as ΔR/R0, where ΔR = (RS − R0)/R0. Here RS is the reflected signal from the heterostructure and R0 is the reflected signal from a nearby heterostructure region without the TMD layers. Since we use the change in the d(ΔR/R0)/dVg signal to identify the correlated states, excitons with a larger oscillator strength and hence higher ΔR/R0 signal exhibit a larger change in d(ΔR/R0)/dVg.
DFT calculations
The moiré unit cell for the free-standing 2H WSe2/MoSe2 HTL with a twist angle of 3.1° contains 2,979 atoms. To calculate the band structure, we first relax the atomic positions using classical force fields as implemented in the LAMMPS code51 (Supplementary Discussion 4 provides details on the HTL geometry and atomic relaxations). DFT calculations were carried out on the relaxed structure using the linear-scaling DFT code SIESTA52. We employ the local-density-approximation exchange–correlation functional53, with a double-zeta plus polarization pseudoatomic orbital basis set, a mesh cutoff of 300 Ry and a vacuum region between periodic images of 15 Å. Spin–orbit coupling was included via the ‘onsite’ approximation54. Electron–ion interactions are described by fully relativistic Troulliers–Martins pseudopotentials55.
For calculations with a non-zero vertical electric field, the same atomic positions as in the zero-field case are used, and we employ a slab dipole correction, in which the electric field used to compensate the dipole of the system is self-consistently computed in every iteration56. Supplementary Discussion 4 reports the DFT band structures with and without the electric field as well as selected wavefunctions of Γ-valley and ±K-valley bands.
t–U–\({{{V}}}\) Hamiltonian
We analyse a three-orbital t–U–\({{{V}}}\) Hamiltonian in the t/U → 0 limit. In this limit, each moiré site can be occupied by at most one hole and no hopping between moiré sites is allowed. To find which configuration of holes ni (where i labels the various moiré sites corresponding to L2 K, ΓA and ΓB orbitals) minimizes the total energy, we use an annealing approach formulated using Monte Carlo simulations. The total energy is given by
where εA, εB and εK(VE) denote the onsite energies of the ΓA, ΓB and L2 K orbitals, respectively. Note that the onsite energy of the L2 K orbital (relative to that of Γ orbitals) depends on the applied electrostatic potential VE. From our DFT calculations, we estimate εA − εB ≈ 20 meV, independent of VE. Also, \({{{V}}}(| {{{{\bf{r}}}}}_{i}-{{{{\bf{r}}}}}_{j}| )=\frac{\exp (-| {{{{\bf{r}}}}}_{i}-{{{{\bf{r}}}}}_{j}| /{L}_{0})}{\epsilon | {{{{\bf{r}}}}}_{i}-{{{{\bf{r}}}}}_{j}| }\) denotes the screened Yukawa interaction between the holes located at positions ri and rj, where ϵ is the dielectric constant (which we set to 4.5) and L0 is the characteristic screening length (which we set to 2 nm). As the K-derived states are highly localized on the L2 WSe2 layer, the corresponding hole positions are assumed to lie in the plane of the layer. In contrast, our DFT calculations show that the Γ-derived states are delocalized across both WSe2 layers, and we, therefore, assume that the corresponding hole positions lie at the midpoint between the layers.
Data availability
The dataset generated and analysed during the current study is available at https://doi.org/10.17861/f4e79017-4043-4318-9315-0793e1fddabc. Source data are provided with this paper.
References
Emery, V. Theory of high-Tc superconductivity in oxides. Phys. Rev. Lett. 58, 2794 (1987).
Zhang, F. & Rice, T. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 37, 3759 (1988).
Dagotto, E. Correlated electrons in high-temperature superconductors. Rev. Mod. Phys. 66, 763 (1994).
Dai, P., Hu, J. & Dagotto, E. Magnetism and its microscopic origin in iron-based high-temperature superconductors. Nat. Phys. 8, 709–718 (2012).
Rohringer, G. et al. Diagrammatic routes to nonlocal correlations beyond dynamical mean field theory. Rev. Mod. Phys. 90, 025003 (2018).
Gross, C. & Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 357, 995–1001 (2017).
Kennes, D. M. et al. Moiré heterostructures as a condensed-matter quantum simulator. Nat. Phys. 17, 155–163 (2021).
Mak, K. F. & Shan, J. Semiconductor moiré materials. Nat. Nanotechnol. 17, 686–695 (2022).
Ghiotto, A. et al. Quantum criticality in twisted transition metal dichalcogenides. Nature 597, 345–349 (2021).
Li, T. et al. Continuous Mott transition in semiconductor moiré superlattices. Nature 597, 350–354 (2021).
Stepanov, P. et al. Untying the insulating and superconducting orders in magic-angle graphene. Nature 583, 375–378 (2020).
Li, T. et al. Charge-order-enhanced capacitance in semiconductor moiré superlattices. Nat. Nanotechnol. 16, 1068–1072 (2021).
Wu, F., Lovorn, T., Tutuc, E. & MacDonald, A. H. Hubbard model physics in transition metal dichalcogenide moiré bands. Phys. Rev. Lett. 121, 026402 (2018).
Zhang, Y., Yuan, N. F. & Fu, L. Moiré quantum chemistry: charge transfer in transition metal dichalcogenide superlattices. Phys. Rev. B 102, 201115 (2020).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Shimazaki, Y. et al. Strongly correlated electrons and hybrid excitons in a moiré heterostructure. Nature 580, 472–477 (2020).
Campbell, A. J. et al. Exciton-polarons in the presence of strongly correlated electronic states in a MoSe2/WSe2 moiré superlattice. npj 2D Mater. Appl. 6, 79 (2022).
Xu, Y. et al. A tunable bilayer Hubbard model in twisted WSe2. Nat. Nanotechnol. 17, 934–939 (2022).
Angeli, M. & MacDonald, A. H. Γ valley transition metal dichalcogenide moiré bands. Proc. Natl Acad. Sci. USA 118, e2021826118 (2021).
Xian, L. et al. Realization of nearly dispersionless bands with strong orbital anisotropy from destructive interference in twisted bilayer MoS2. Nat. Commun. 12, 5644 (2021).
Kaushal, N., Morales-Durán, N., MacDonald, A. H. & Dagotto, E. Magnetic ground states of honeycomb lattice Wigner crystals. Commun. Phys. 5, 289 (2022).
An, L. et al. Interaction effects and superconductivity signatures in twisted double-bilayer WSe2. Nanoscale Horiz. 5, 1309–1316 (2020).
Pei, D. et al. Observation of Γ-valley moiré bands and emergent hexagonal lattice in twisted transition metal dichalcogenides. Phys. Rev. X 12, 021065 (2022).
Gatti, G. et al. Flat Γ moiré bands in twisted bilayer WSe2. Phys. Rev. Lett. 131, 046401 (2023).
Foutty, B. A. et al. Tunable spin and valley excitations of correlated insulators in Γ-valley moiré bands. Nat. Mater. 22, 731–736 (2023).
Magorrian, S. et al. Multifaceted moiré superlattice physics in twisted WSe2 bilayers. Phys. Rev. B 104, 125440 (2021).
Vitale, V., Atalar, K., Mostofi, A. A. & Lischner, J. Flat band properties of twisted transition metal dichalcogenide homo- and heterobilayers of MoS2, MoSe2, WS2 and WSe2. 2D Mater. 8, 045010 (2021).
Back, P. et al. Giant paramagnetism-induced valley polarization of electrons in charge-tunable monolayer MoSe2. Phys. Rev. Lett. 118, 237404 (2017).
Zhou, Y. et al. Bilayer Wigner crystals in a transition metal dichalcogenide heterostructure. Nature 595, 48–52 (2021).
Movva, H. C. et al. Tunable Γ-K valley populations in hole-doped trilayer WSe2. Phys. Rev. Lett. 120, 107703 (2018).
Rigosi, A. F., Hill, H. M., Li, Y., Chernikov, A. & Heinz, T. F. Probing interlayer interactions in transition metal dichalcogenide heterostructures by optical spectroscopy: MoS2/WS2 and MoSe2/WSe2. Nano Lett. 15, 5033–5038 (2015).
Jones, A. M. et al. Spin–layer locking effects in optical orientation of exciton spin in bilayer WSe2. Nat. Phys. 10, 130–134 (2014).
Brotons-Gisbert, M. et al. Spin-layer locking of interlayer excitons trapped in moiré potentials. Nat. Mater. 19, 630–636 (2020).
Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).
Kaushal, N. & Dagotto, E. Moiré Kanamori-Hubbard model for transition metal dichalcogenide homobilayers. Phys. Rev. B 107, L201118 (2023).
Morales-Durán, N., Potasz, P. & MacDonald, A. H. Magnetism and quantum melting in moiré-material Wigner crystals. Phys. Rev. B 107, 235131 (2023).
Matty, M. & Kim, E.-A. Melting of generalized Wigner crystals in transition metal dichalcogenide heterobilayer moiré systems. Nat. Commun. 13, 7098 (2022).
Courtade, E. et al. Charged excitons in monolayer WSe2: experiment and theory. Phys. Rev. B 96, 085302 (2017).
Wang, Z., Chiu, Y.-H., Honz, K., Mak, K. F. & Shan, J. Electrical tuning of interlayer exciton gases in WSe2 bilayers. Nano Lett. 18, 137–143 (2018).
Naik, M. H. et al. Intralayer charge-transfer moiré excitons in van der Waals superlattices. Nature 609, 52–57 (2022).
Raja, A. et al. Coulomb engineering of the bandgap and excitons in two-dimensional materials. Nat. Commun. 8, 15251 (2017).
Chen, D. et al. Excitonic insulator in a heterojunction moiré superlattice. Nat. Phys. 18, 1171–1176 (2022).
Sidler, M. et al. Fermi polaron-polaritons in charge-tunable atomically thin semiconductors. Nat. Phys. 13, 255–261 (2017).
Efimkin, D. K. & MacDonald, A. H. Many-body theory of trion absorption features in two-dimensional semiconductors. Phys. Rev. B 95, 035417 (2017).
Gao, S., Liang, Y., Spataru, C. D. & Yang, L. Dynamical excitonic effects in doped two-dimensional semiconductors. Nano Lett. 16, 5568–5573 (2016).
Brixner, L. H. Preparation and properties of the single crystalline AB2-type selenides and tellurides of niobium, tantalum, molybdenum and tungsten. J. Inorg. Nucl. Chem. 24, 257–263 (1962).
Laturia, A., Van de Put, M. L. & Vandenberghe, W. G. Dielectric properties of hexagonal boron nitride and transition metal dichalcogenides: from monolayer to bulk. npj 2D Mater. Appl. 2, 6 (2018).
Baek, H. et al. Highly energy-tunable quantum light from moiré-trapped excitons. Sci. Adv. 6, eaba8526 (2020).
Brotons-Gisbert, M. et al. Moiré-trapped interlayer trions in a charge-tunable WSe2/MoSe2 heterobilayer. Phys. Rev. X 11, 031033 (2021).
Thompson, A. P. et al. LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 271, 108171 (2022).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys.: Condens. Matter 14, 2745 (2002).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Fernández-Seivane, L., Oliveira, M. A., Sanvito, S. & Ferrer, J. On-site approximation for spin-orbit coupling in linear combination of atomic orbitals density functional methods. J. Phys.: Condens. Matter 18, 7999 (2006).
Troullier, N. & Martins, J. L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 43, 1993–2006 (1991).
Papior, N., Lorente, N., Frederiksen, T., García, A. & Brandbyge, M. Improvements on non-equilibrium and transport Green function techniques: the next-generation TRANSIESTA. Comput. Phys. Commun. 212, 8–24 (2017).
Acknowledgements
We thank J. Ruhman for insightful discussions. This work was supported by the EPSRC (grant nos. EP/P029892/1 and EP/L015110/1), and the ERC (grant no. 725920) (A.J.C., M.B.-G., H.B., T.V.I., A.B. and B.D.G). V.V. and J.L. acknowledge funding from the EPSRC (grant no. EP/S025324/1). This work used the ARCHER2 UK National Supercomputing Service via J.L.’s membership of the HEC Materials Chemistry Consortium of UK, which is funded by the EPSRC (EP/L000202). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 101067977. M.B.-G. is supported by a Royal Society University Research Fellowship. B.D.G. is supported by a Wolfson Merit Award from the Royal Society and a Chair in Emerging Technology from the Royal Academy of Engineering. K.W. and T.T. acknowledge support from JSPS KAKENHI (grant nos. 19H05790, 20H00354 and 21H05233).
Author information
Authors and Affiliations
Contributions
A.J.C. performed the experimental measurements, except for the second-harmonic generation measurements which were performed by A.B. and T.V.I. A.J.C., M.B.-G. and B.D.G. analysed the data. H.B. fabricated the sample. V.V. and J.L. performed the theoretical calculations. T.T. and K.W. grew the hBN crystals. B.D.G. and J.L. conceived and supervised the project. A.J.C., V.V., M.B.-G, J.L. and B.D.G. wrote the paper with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks David Ruiz-Tijerina, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Twist angle homogeneity in the heterotrilayer.
a Optical micrograph of the stacked heterobilayer (HBL) and heterotrilayer (HTL) device regions before encapsulation in hBN. b Spatial map of the ΔR/R0 integrated in the spectral range 739 nm to 741 nm, with the HTL region outlined in green. The numbered spots indicate the measured locations. The red circle (L1) identifies the location measured in the main text. The lateral size of the spot indicates an estimate of the confocal collection spot size. cVg dependence of d(ΔR/R0)/dE in location 6 (L6) of the HTL. dνh dependence of the d(ΔR/R0)/dVg in L6. The dashed lines indicate integer fractional fillings of holes in each moiré unit cell. e,f As described for panels (c,d) for L10. g,h As described for panels (c,d) for L2. The dashed red boxes identify the highly reproducible signature that occurs for νh = 1.
Extended Data Fig. 2 Exciton-polaron behaviour under band realignment.
a Density plot showing the VE dependence of the d(ΔR/R0)/dE when the hole filling is fixed at νh = 2. The white dashed line indicates an abrupt change in the observed resonances. At VE = + 2V, ΔE1 is estimated to be 25 meV, extracted from Lorentizian oscillator fits to the resonances. For VE = + 3V, ΔE2 and ΔE3 are found to be 21 meV and 15 meV respectively. b-d Density plots of the Vg dependence of d(ΔR/R0)/dE when a constant VE of + 1 V (b), + 2 V (c) and + 3 V (d) is applied. For VE = + 1V and VE = + 2V, the energy splittings between AP\({}_{W,L1}^{+}\) and AP\({}_{W,L2}^{+}\) (ΔE1) are found to be 23 meV and 24 meV respectively. This is in good agreement with the ΔE1 estimated at VE = + 2 V in panel (a). As previously shown in the main text, the direct momentum electron-hole pairs at ± K are dressed by holes resident in the Γ derived moiré valence band, forming a correlated state (νΓ = 2, νK = 0). For VE = + 3V and νh = 2, the energy splitting between X\({}_{W,L1}^{0}\) and AP\({}_{W,L2}^{+}\) (ΔE2) is measured to be 15 meV, while the splitting between AP\({}_{W,L2}^{+}\) and RP\({}_{W,L2}^{+}\) (ΔE3) is measured to be 24 meV. These are close to the values extracted for ΔE2 and ΔE3 in panel a, and hence allow us to identify the three resonances for VE > + 2.3V as X\({}_{W,L1}^{0}\), AP\({}_{W,L2}^{+}\) and RP\({}_{W,L2}^{+}\) in order of increasing energy. As previously shown by the polarisation resolved measurements under an applied magnetic field (Fig. 3a,b in the main text) for VE = + 3V, AP\({}_{W,L2}^{+}\) is formed by an exciton dressed by holes in the moiré band deriving from ± K point in L2. We therefore determine that at VE = + 2.3V in panel a the holes in the ΓB orbital are suddenly transferred to the L2 K orbital, forming a correlated state with νΓ = 1 and νK = 1. e To characterise the abruptness of the hole transfer, we fit the full width half maximum of the d(ΔR/R0)/dVE at 1.68 eV. The solid black line represents a Lorentzian fit to the data, from which a full width half maximum of 0.53 V is extracted, centred around VE = 2.30 V.
Extended Data Fig. 3 Enhancement of magnetic interactions for K orbital holes.
a, Vg dependence of d(ΔR/R0)/dE at VE = 0V. The white arrow indicates the L2 WSe2 attractive polaron resonance. b,cσ+ (b) and σ− resolved B-field sweep of d(ΔR/R0)/dE at VE = 0 V and Vg = − 2.4 V as indicated by the white dashed line in panel (a). d-f, As described for panels (a-c) for VE = +2 V. g-i As described for panels (a-c) for VE = +3 V. For Vg = − 2.4 V for both VE = + 0 V and VE = +2 V (νΓ ~ 2, νK = 0) the attractive polaron formed from the exciton in the upper WSe2 layer (L2) AP\({}_{W,L2}^{+}\) exhibits a very small shift in energy with magnetic field. In contrast, for VE +3 V, and Vg = − 2.4 V (νΓ ~ 1, νK ~ 1) AP\({}_{W,L2}^{+}\) exhibits both a huge positive g-factor and a large degree of spin polarisation, consistent with carriers loaded at the ± K points.
Extended Data Fig. 4 Temperature dependence of the strongly correlated electronic states in the heterotrilayer.
a, Vg dependence of d(ΔR/R0)/dE at a sample temperature of 12 K, b 40 K, c 95 K and d 130 K. eνh dependence of d(ΔR/R0)/dVg at 12 K, f 40 K, g 95 K and h 130 K. The abrupt changes in the d(ΔR/R0)/dVg signal that indicate the formation of correlated hole states disappear as the temperature is increased.
Extended Data Fig. 5 Analysis of the temperature dependence of strongly correlated electronic states in the heterotrilayer.
a, Second derivative of ΔR/R0 with respect to Vg integrated in the spectral range 1.59 to 1.76 eV for different temperatures. We observe peaks in Σ∣ d 2(ΔR/R0)/ d 2Vg∣ at νe,h = ± 1, ± 2. We fit the peaks at νh = 1, 2 using a Gaussian and integrate the peak area to provide an estimate of the strength of the correlated states at νh = 1, 2. b, Evolution with temperature of the normalised integrated area of the peaks at νh = 1, 2 in \(\Sigma \left(| \right.\) d 2(ΔR/R0)/d\({V}_{g}^{2}|\) (indicated by the vertical dashed lines). By fitting an arctan function to the temperature dependence of the normalised spectral weight, we estimate the temperature TC at which the strongly correlated states disappear. We find TC ~ 98 K for νh = 1 and TC ~ 59 K for νh = 2. The TC for νh = 1 corresponds to a charge gap of 8.4 meV.
Extended Data Fig. 6 Charge neutrality region in the heterotrilayer.
Vg dependence of the d(ΔR/R0)/dE signal in the heterotrilayer. The solid white lines indicate the charge neutrality region, while the dashed lines indicate where correlated states are formed at integer fillings of the moiré superlattice. The labelling of the charge neutrality region is omitted in the main manuscript to avoid over-crowding the figure.
Extended Data Fig. 7 DFT calculations for R- versus H-stacking.
Top valence bands and wavefunction densities at high-symmetry points for two different stackings of a 2H-WSe2 bilayer on a twisted MoSe2 layer. Top two valence bands derive from Γ valley of WSe2 and are labeled as ΓA (top, light purple) and ΓB (bottom, dark purple). Bands deriving from ± K valley of WSe2 are also highlighted in red and blue, respectively. See the main manuscript for more details. Top panel: R-stacked (θ = 3. 1∘). Wavefunction densities of ΓA and ΓB bands at the k valley of the moiré BZ and of K(L1) and K(L2) at the γ valley of the moiré BZ. Bottom panel: same as top valley but for H-stacked (θ = 56. 9∘). For twisted homobilayers (for example WSe2) R-stacking is necessary to obtain ground state Γ-derived moiré bands with a honeycomb lattice20,27. However, in the case of the monolayer MoSe2 / 2-H natural WSe2 bilayer (HTL) device, we find that DFT calculations cannot distinguish between R- and H-stacked HTLs in terms of band structure and localization of wavefunctions. As shown in the figure we find that the two different configurations result in very similar electronic band structures at the top of the valence manifold. Moreover, even though R-stacked and H-stacked HTLs exhibit different stacking types, the relative localization of states from ΓA, ΓB and K(L2) is the same for both HTLs: in particular, states from ΓB and K(L2) are localized in the same regions resulting in the same predictions for optical properties of both HTLs.
Supplementary information
Supplementary Information
Supplementary Discussions 1–4 and Figs. 1–9.
Source data
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Extended Data Fig. 2
Statistical source data.
Source Data Extended Data Fig. 5
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Campbell, A.J., Vitale, V., Brotons-Gisbert, M. et al. The interplay of field-tunable strongly correlated states in a multi-orbital moiré system. Nat. Phys. 20, 589–596 (2024). https://doi.org/10.1038/s41567-024-02385-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-024-02385-4