Abstract
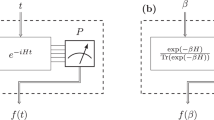
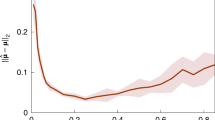
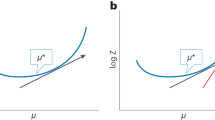
The behaviour of a system is determined by its Hamiltonian. In many cases, the exact Hamiltonian is not known and has to be extracted by analysing the outcome of measurements. We study the problem of learning a local Hamiltonian H to a given precision, supposing either we are given copies of its Gibbs state ρ = e−βH/Tr(e−βH) at a known inverse temperature β or we have access to unitary real-time evolution e−itH for a known evolution time t. Improving on recent results, we show how to learn the coefficients of a local Hamiltonian H to error ε with S = O(logN/(βε)2) Gibbs states or with Q = O(logN/(tε)2) runs of the real-time evolution, where N is the number of qubits in the system and if β < βc and t < tc for some critical inverse temperature βc and critical evolution time tc. We design a classical post-processing algorithm with time complexity linear in the sample size in both cases, namely, O(NS) and O(NQ). In the Gibbs-state input case, we prove a matching lower bound, showing that our algorithm’s sample complexity is optimal, and hence, our time complexity is also optimal.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
Data availability
Data sharing is not applicable to this paper as no datasets were generated or analysed during the current study.
References
Bairey, E., Arad, I. & Lindner, N. H. Learning a local Hamiltonian from local measurements. Phys. Rev. Lett. 122, 020504 (2019).
Qi, X.-L. & Ranard, D. Determining a local Hamiltonian from a single eigenstate. Quantum 3, 159 (2019).
Evans, T. J., Harper, R. & Flammia, S. T. Scalable Bayesian Hamiltonian learning. Preprint at https://arxiv.org/abs/1912.07636 (2019).
Bairey, E., Guo, C., Poletti, D., Lindner, N. H. & Arad, I. Learning the dynamics of open quantum systems from their steady states. New J. Phys. 22, 032001 (2020).
Karger, D. & Srebro, N. Learning Markov networks: maximum bounded tree-width graphs. in Proc. Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA ’01 392–401 (SIAM, 2001).
Abbeel, P., Koller, D. & Ng, A. Y. Learning factor graphs in polynomial time and sample complexity. J. Mach. Learn. Res. 7, 1743–1788 (2006).
Santhanam, N. P. & Wainwright, M. J. Information-theoretic limits of selecting binary graphical models in high dimensions. IEEE Trans. Inf. Theory 58, 4117–4134 (2012).
Bresler, G., Mossel, E. & Sly, A. Reconstruction of Markov random fields from samples: some observations and algorithms. SIAM J. Comput. 42, 563–578 (2013).
Bresler, G. Efficiently learning Ising models on arbitrary graphs. in Proc. Forty-Seventh Annual ACM on Symposium on Theory of Computing—STOC ’15 771–782 (ACM Press, 2015).
Vuffray, M., Misra, S., Lokhov, A. & Chertkov, M. Interaction screening: efficient and sample-optimal learning of Ising models. in Advances in Neural Information Processing Systems Vol. 29 (Curran Associates, 2016).
Klivans, A. & Meka, R. Learning graphical models using multiplicative weights. in 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS) 343–354 (IEEE, 2017).
Kindermann, R. & Snell, J. L. Markov Random Fields and their Applications (American Mathematical Society, 1980).
Clifford, P. Markov random fields in statistics. in Disorder in Physical Systems. A Volume in Honour of John M. Hammersley (Clarendon Press, 1990).
Lauritzen, S. Graphical Models (Clarendon Press, 1996).
Jaimovich, A., Elidan, G., Margalit, H. & Friedman, N. Towards an integrated protein–protein interaction network: a relational Markov network approach. J. Comput. Biol. 13, 145–164 (2006).
Koller, D. & Friedman, N. Probabilistic Graphical Models: Principles and Techniques (MIT Press, 2009).
Li, S. Z. Markov Random Field Modeling in Image Analysis (Springer, 2009).
Anshu, A., Arunachalam, S., Kuwahara, T. & Soleimanifar, M. Sample-efficient learning of interacting quantum systems. Nat. Phys. 17, 931–935 (2021).
Chow, C. & Liu, C. Approximating discrete probability distributions with dependence trees. IEEE Trans. Inf. Theory 14, 462–467 (1968).
Haah, J., Kothari, R. & Tang, E. Optimal learning of quantum Hamiltonians from high-temperature Gibbs states. Preprint at https://arxiv.org/abs/2108.04842 (2023).
Kuwahara, T., Kato, K. & Brandão, F. G. S. L. Clustering of conditional mutual information for quantum Gibbs states above a threshold temperature. Phys. Rev. Lett. 124, 220601 (2020).
Huang, H.-Y., Tong, Y., Fang, D. & Su, Y. Learning many-body Hamiltonians with Heisenberg-limited scaling. Phys. Rev. Lett. 130, 200403 (2023).
Dutkiewicz, A., O’Brien, T. E. & Schuster, T. The advantage of quantum control in many-body Hamiltonian learning. Preprint at https://arxiv.org/abs/2304.07172 (2023).
Acknowledgements
Some of this work was performed while E.T. was a research intern at Microsoft Quantum. E.T. is supported in part by the NSF GRFP (DGE-1762114). R.K. and E.T. thank M. Silva for early discussions about this problem. R.K. thanks V. P. Pingali for many helpful discussions about this problem and multivariable calculus. E.T. thanks A. Anshu for the question about the strong convexity of the log-partition function and A. Klivans for discussions about the state of the art in learning classical Hamiltonians. We also thank H.-Y. Huang for raising the question of learning a Hamiltonian from its real-time evolution.
Author information
Authors and Affiliations
Contributions
All authors have contributed equally to the formulation of the problem, algorithm design, its performance analysis and writing this manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Yihui Quek and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary text.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Haah, J., Kothari, R. & Tang, E. Learning quantum Hamiltonians from high-temperature Gibbs states and real-time evolutions. Nat. Phys. (2024). https://doi.org/10.1038/s41567-023-02376-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41567-023-02376-x