Abstract
A hallmark of symmetry-protected topological phases are topological boundary states, which are immune to perturbations that respect the protecting symmetry. It is commonly believed that any perturbation that destroys such a topological phase simultaneously destroys the boundary states. However, by introducing and exploring a weaker sub-symmetry requirement on perturbations, we find that the nature of boundary state protection is in fact more complex. Here we demonstrate that the boundary states are protected by only the sub-symmetry, using Su–Schrieffer–Heeger and breathing kagome lattice models, even though the overall topological invariant and the associated topological phase can be destroyed by sub-symmetry-preserving perturbations. By precisely controlling symmetry breaking in photonic lattices, we experimentally demonstrate such sub-symmetry protection of topological states. Furthermore, we introduce a long-range hopping symmetry in breathing kagome lattices, which resolves a debate on the higher-order topological nature of their corner states. Our results apply beyond photonics and could be used to explore the properties of symmetry-protected topological phases in the absence of full symmetry in different physical contexts.
Similar content being viewed by others
Main
Symmetry-protected topological (SPT) phases of matter are ubiquitous in nature and exist on versatile platforms including condensed-matter physics, ultracold atomic gases and photonics1,2. Topological insulators (TIs) induced by spin–orbit coupling, which are protected by time-reversal symmetry, are a paradigm for SPT phases of matter1,2,3. In topological crystalline insulators, a crystalline point group symmetry protects topological metallic boundary states1,4.
Imagine an SPT phase with a topological invariant characterizing the bulk states and the associated symmetry-protected boundary states. Any perturbation that respects the protecting symmetries will not destroy these boundary states or change the topological invariant without closing the gap between bands1,2. However, as pictured in Fig. 1, the situation can be more complex: there are perturbations that preserve the topological invariant but oppose the existence of boundary states5,6 and, vice versa, there are perturbations that leave the boundary states unhurt while destroying the topological invariant7. Here we explore the underlying physics for the latter scenario by using the concept of sub-symmetry (SubSy), where the symmetry equation, involving the Hamiltonian and a symmetry operator, does not hold in the whole Hilbert space, but only in its subspace. For the prototypical one-dimensional (1D) Su–Schrieffer–Heeger (SSH) and two-dimensional (2D) breathing kagome lattice (BKL) models, the SubSys arise from their chiral symmetries, which restrict the possibilities of coupling between sublattices (rigorously defined below). Here the SubSy means that the symmetry equation holds on only one sublattice.
A set of perturbations, which preserves the topological invariant (or invariants) and respects a particular symmetry (or symmetries), is encircled with a grey line. Every boundary state, when it exists, is protected with its pertinent SubSy. In the illustration, two sets of SubSy-preserving perturbations (encircled with red and green lines) are sketched, but their number depends on the actual system. At the overlap region, one has an SPT phase with a topological invariant (illustrated as a Möbius strip) characterizing the bulk (illustrated with a thick black line), and all associated boundary states (illustrated with red and green circles). For the SSH lattice, the SPT phase is protected by a chiral symmetry (with the implicit assumption of inversion symmetry). The topological invariant is protected by the inversion symmetry (even when the chiral symmetry is broken). The edge state on the A sublattice is protected with A-SubSy, which is defined by a chiral symmetry equation that holds solely on the A sublattice. The same holds for the edge state on the B sublattice with B-SubSy as the protecting sub-symmetry. For the BKL with negligible long-range hopping (see main text), the C3 symmetry protects the topological invariant, whereas there are three SubSys corresponding to three BKL sublattices, which protect the pertinent higher-order topological corner states. See text for details.
We demonstrate, theoretically and experimentally, that the boundary states in the SSH and BKL models are protected by their pertinent SubSy. Any SubSy-preserving perturbation will leave its corresponding boundary state eigenvalue at zero, even though the bulk topological invariant is lost. We utilize zigzag and twisted lattices, and ‘bridge’ waveguides to experimentally introduce SubSy-breaking and SubSy-preserving perturbations in a controlled manner and thereby demonstrate SubSy-protected topological states. In the case of non-negligible long-range hopping (that is, non-negligible coupling between distant lattice sites) in BKLs, we find that SubSy and an additional long-range hopping symmetry are sufficient to protect the corner states. Our experiments are performed in photonic structures, which have been established as a fertile platform for exploring novel topological phenomena8,9,10. The main message from our findings is summarized in Fig. 1.
The SSH lattice illustrated in Fig. 2a represents a typical 1D topological model, originally used to describe polyacetylene11. It has subsequently been experimentally realized on versatile platforms including photonics and nanophotonics12,13,14,15, plasmonics16 and quantum optics17 and in the context of parity–time symmetry and nonlinear non-Hermitian phenomena18,19.
a, The SSH model. b, Spectra of the unperturbed (black circles) and the A-SubSy-perturbed system (t1 = 0.1, t2 = 1). In all subplots, the blue crosses are perturbed bands, the red circle is the perturbed left edge state at zero energy, and the green cross is the perturbed right edge state. c, Modal structure of the unperturbed (black) and the perturbed left (red) and right (green) edge states. The black modes are shifted up for better visibility. d,e, Left: experimental images of A-SubSy-preserving lattice with B–B coupling (d) and A-SubSy-breaking lattice with A–A coupling (e). The white arrows indicate that solely the left-most waveguide (A sublattice site) is excited at z = 0. Middle: output intensity patterns of the probe beam after propagating 20 mm through corresponding lattices in the left panels, respectively. The intensity profile in the A-SubSy-preserving lattice resides solely on the A sublattice (d), whereas the intensity profile in the A-SubSy-breaking lattice is present on both A and B sublattices (e), which demonstrates SubSy protection of the left topological edge mode. The lattice constant (size of the unit cell) is 40 μm, and the twist angle is 57°. Right: numerical simulations in the middle panels agree with the related measurements. f,g, Left: experimental images of A-SubSy-preserving zigzag lattice with periodic B–B coupling (f) and A-SubSy-breaking lattice with A–A coupling (g). Middle: output intensity patterns after 20 mm of propagation (the probe beam excites the bottom site). The intensity profile in the A-SubSy-preserving lattice resides solely on the A sublattice (f), whereas it leaks onto the B sublattice for the A-SubSy-breaking case (g). This again demonstrates the SubSy protection of the edge mode \(\left| {{A_{\mathrm{L}}}} \right\rangle\). For these experiments, the lattice constant is 55 μm, and the twist angle is 60°. Right: numerical simulations to ten-times-longer propagation distance corroborate our experimental results.
The SSH lattice is composed of A and B sublattices (Fig. 2a), with the Hamiltonian \(H_{\mathrm{SSH}} ={\varSigma_n} {(t_1 b_n^{\dagger} a_n + t_2a_{n + 1}^{\dagger} b_n + {\mathrm{h.c.}})}\), where an is the annihilation operator at an A sublattice site in the nth unit cell, with an analogous definition for bn, while t1 and t2 are the intracell and intercell coupling strengths, respectively. Its topological phase is protected by the chiral symmetry
where \({{\varSigma }}_z = P_{\mathrm{A}} - P_{\mathrm{B}}\) and PA (PB) denotes the projection operator on the A (B) sublattice (Methods). The system has a trivial phase for t1 > t2 and a topologically non-trivial phase for t1 < t2, with the latter being characterized by the Zak phase of π and two topologically protected edge states at zero energy (Fig. 2b). The amplitudes of the left edge state \(\left| {{A_{\mathrm{L}}}} \right\rangle\) are non-zero solely on the A sublattice, that is, \({{P_{\mathrm{A}}}}\left| {A_{\mathrm{L}}} \right\rangle = \left| {{A_{\mathrm{L}}}} \right\rangle\), and \(P_{\mathrm{B}}\left| {{A_{\mathrm{L}}}} \right\rangle = 0\), and analogously for the right edge state \(\left| {{B_{\mathrm{R}}}} \right\rangle\) (Fig. 2c).
The concept of SubSy focuses on perturbations that break the chiral symmetry but preserve a less strict SubSy requirement. This provides a theoretical framework and generalizes the partial chiral symmetry-breaking case proposed previously in ref. 7. There are two SubSys in the SSH model, the A-SubSy and the B-SubSy, which are defined by
The most general perturbation in the couplings is of the form HAB + HAA + HBB, which implies that the hopping parameter between any two lattice sites (irrespective of distance) can be changed without any restrictions. Here \(H_{\mathrm{AB}} = \mathop {\varSigma}\nolimits_{m,n} {\left( {s_{ab}^{m,n}a_m^{\dagger} b_n + {\mathrm{h.c.}}} \right)}\) denotes couplings between the A and B sublattice sites (A–B coupling), where \(s_{ab}^{m,n}\) are the individual coupling strengths, with an analogous definition for the A–A (HAA) and B–B (HBB) couplings (see Methods for details).
Without loss of generality, we consider A-SubSy-preserving perturbations, which are of the form H′ = HAB + HBB; they are more restrictive than general perturbations but less restrictive than chiral symmetry-preserving perturbations (HAB). Perturbations involving the A–A coupling (HAA) break the A-SubSy. We emphasize that A-SubSy-preserving perturbations can be periodic (that is, respecting the lattice symmetry) or local (for example, perturbing only one coupling between two lattice sites) or even feature disorder.
One of our key results is that any such perturbation, if it respects the A-SubSy, will not destroy the left edge zero-energy state \(\left| {{A_{\mathrm{L}}}} \right\rangle\) (and fully analogously for the B-SubSy), as illustrated in Fig. 2a–c. The theoretical argument for this statement is made possible by the formulation of SubSy via projection operators in equation (2): because HAB preserves the chiral symmetry, the edge states are protected under such perturbations until the gap closes. B–B perturbations do not affect \(\left| {{A_{\mathrm{L}}}} \right\rangle\) because HBBPA = 0, which leads to \(H_{\mathrm{BB}}\left| {{A_{\mathrm{L}}}} \right\rangle = H_{\mathrm{BB}}P_{\mathrm{A}}\left| {{A_{\mathrm{L}}}} \right\rangle = 0\). Thus, \(\left| {{A_{\mathrm{L}}}} \right\rangle\) is protected under A-SubSy-preserving perturbations H′ = HAB + HBB. However, the right edge zero-energy state \(\left| {{B_{\mathrm{R}}}} \right\rangle\) is not protected because the HBB component affects this state. Moreover, HBB perturbations generally break both the chiral symmetry and the Zak phase quantization.
SubSy protection of edge states is illustrated in Fig. 2b,c, which show the spectra and the eigenmode structure for the case of a single randomly chosen A-SubSy-preserving perturbation. The energy of the perturbed left edge mode \(\left| {{A}_{\mathrm{L}}^\prime } \right\rangle\) is intact, but that of the right edge mode as well as the whole spectrum is altered by A-SubSy-preserving perturbations (Fig. 2b). The perturbed mode \(\left| {{A}_{\mathrm{L}}^\prime } \right\rangle\) resides solely on the A sublattice, that is, \(\left| {\left\langle {{{A}}_{\mathrm{L}}^\prime |P_{\mathrm{A}}{{A}}_{\mathrm{L}}^\prime } \right\rangle } \right|^2 = 1\); however, its structure can differ from the unperturbed mode (Fig. 2c). Detailed numerical analysis confirms that SubSy requirement is essential for protecting the edge states (Supplementary Information).
To experimentally test such edge-state protection with respect to the SubSy-preserving perturbations, we break the chiral symmetry in a controlled fashion. To this end, we introduce the appropriate A–A or B–B hopping by twisting the SSH lattice into the angled structure illustrated in Fig. 2d,e (left), which either breaks the A-SubSy (Fig. 2e) or preserves it (Fig. 2d). The probing is performed by launching a focused beam into the left-most waveguide on the A sublattice. In Fig. 2d (middle), the output intensity resides dominantly on the A sublattice, indicating that the left edge mode is topologically protected when the A-SubSy is preserved. For a direct comparison, in Fig. 2e (middle), we show the intensity of the same excitation beam propagating through the A-SubSy-breaking lattice. The presence of light in the second waveguide, that is, on the B sublattice, indicates that it is no longer a topologically protected edge mode12,19. Numerical simulations (Fig. 2d,e, right) agree with experimental results.
Perturbations in the twisted SSH lattices (Fig. 2d,e) are localized. To experimentally probe the robustness of edge states under periodic A-SubSy-preserving (Fig. 2f) or A-SubSy-breaking (Fig. 2g) perturbations, we fabricated two zigzag photonic SSH lattices. The zigzag lattices plotted in Fig. 2f,g (left) are oriented such that the bottom site belongs to the A sublattice. By exciting the bottom edge waveguide in the A-SubSy-preserving lattice, we observe protection of the edge mode as light populates solely the A sublattice, without coupling to the bulk (Fig. 2f, middle). An identical excitation in the A-SubSy-breaking lattice (Fig. 2g, middle) clearly indicates that the edge mode is no longer topologically protected as light leaks into the B sublattice. Numerical simulations for much longer propagation distances (Fig. 2f,g, right) corroborate our experimental results. We emphasize that the zigzag lattice in Fig. 2f (left) breaks both the inversion and chiral symmetries, yet the edge mode \(\left| {{A_{\mathrm{L}}}} \right\rangle\) is protected by the A-SubSy.
The kagome lattice is an inexhaustible golden vein of intriguing physics, attracting the broad interest of the scientific community. BKLs, illustrated in Fig. 3a, have been classified as higher-order topological insulators (HOTIs), where topologically protected corner states were observed20,21,22,23,24,25,26. HOTIs are a new class of topological materials27, found in condensed-matter, networks of resonators, photonic and acoustic systems20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39. The corner states in the BKLs were initially considered as HOTI states protected by the generalized chiral symmetry and the C3 crystalline symmetry20. However, it was later debated that they are not HOTI states40,41,42 because they are not protected by some specific long-range hopping perturbations obeying these symmetries40. In our discussion of SubSy-protected corner BKL states, we clarify this debated issue.
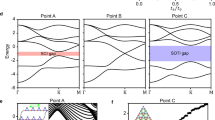
a, Sketch of the rhombic BKL with three sublattices. b, Illustration of the LRHS condition expressed in equation (4), for which the coupling between two sites indicated with red links must be equal, and the same for the coupling indicated with two blue links, and so on. c–e, Eigenvalue spectra of the rhombic BKL flake with 29 lattice sites along one edge for different perturbations. c, Ensemble of spectra for a set of 70 randomly chosen A-SubSy-preserving perturbations H′ = HBB + HCC + HBC of various strengths quantified by δ′, which leaves the zero-energy mode (red cross) intact. d, Bandgap structure of the unperturbed rhombic BKL flake (t1 = 0.1, t2 = 1). The rhombic BKL flake has a single corner state shown in the inset. e, Spectra for a set of 70 perturbations H′ + H″, which respect the A-SubSy and the LRHS (H″ = HAC + HAB). The magnitude of perturbations H′ is fixed at δ′ = 0.05, whereas that of the H″ perturbations, δ″ is varied. The zero-energy mode (red cross) is protected despite the presence of long-range hopping. In c and e, we calculate 70 spectra for 70 different perturbations, which are plotted one on top of the other. What appears as a single red cross at zero value indicates that for any perturbation, the zero mode is protected. A slight spread of red crosses for δ″ > 0.12 in e indicates that the zero mode becomes adjacent to the band modes (blue crosses) when finite-size effects become relevant. f, FCA and the mode densities (ρ and σ) calculated for perturbations from e (Methods).
BKLs are composed of three sublattices (A, B and C), featuring intracell and intercell hopping amplitudes t1 and t2, respectively (Fig. 3a and Methods). The bulk polarizations are the topological invariants that characterize the topological phase: for t1 < t2, the system is in the non-trivial phase with \(P_x = P_y = \frac{1}{3}\), whereas for t1 > t2, the polarizations are zero20,21. The BKL Hamiltonian HK possesses C3 symmetry and the generalized chiral symmetry \({{\varSigma }}_3H_{\mathrm{K}}{{\varSigma }}_3^{ - 1} + {{\varSigma }}_3^2H_{\mathrm{K}}{{\varSigma }}_3^{ - 2} = - H_{\mathrm{K}}\) (ref. 20). Here \({{\varSigma }}_3 = P_{\mathrm{A}} + {\mathrm{e}}^{{\mathrm{i}} \frac{{2\uppi }}{3}}P_{\mathrm{B}} + {\mathrm{e}}^{ - {\mathrm{i}}\frac{{2\uppi }}{3}}P_{\mathrm{C}}\) is the symmetry operator, where \(P_i,i \in \left\{ {\mathrm{A,B,C}} \right\}\) are the projection operators. The generalized chiral symmetry yields three equations
defining three SubSys corresponding to the three sublattices.
Our theoretical results on BKLs are presented in Fig. 3. We consider a rhombic flake illustrated in Fig. 3a, which has one zero-energy corner state \(H_{\mathrm{K}}\left| {{A}_{\mathrm{cor}}} \right\rangle = 0\) residing on the A sublattice, \(P_{\mathrm{A}}\left| {{{A}}_{\mathrm{cor}}} \right\rangle = \left| {{A}_{\mathrm{cor}}} \right\rangle\). The bandgap structure of one such flake is shown in Fig. 3d. First, we consider perturbations between B–B, C–C and B–C sites, H′ = HBB + HCC + HBC, which obey the A-SubSy, yet breaking the generalized chiral symmetry. These perturbations obey H′PA = 0, which implies \(H^\prime \left| {{A}_{\mathrm{cor}}} \right\rangle = H^\prime P_{\mathrm{A}}\left| {{A}_{\mathrm{cor}} } \right\rangle = 0\), that is, any such perturbation does not affect the corner state. This is illustrated in Fig. 3c that shows the bandgap structure, with the corner state indicated by red crosses, for a set of randomly chosen perturbations H′ of various magnitudes quantified by δ′. These perturbations are randomly chosen from a set that respect both A-SubSy and the lattice symmetries (Methods). Interestingly, at some higher perturbation strengths, \(\left| {A_{\mathrm{cor}}} \right\rangle\) can become a bound state in the continuum43.
Next, we consider the A-SubSy-preserving perturbations between A–B and A–C sites: H″ = HAC + HAB. Such perturbations can affect the zero-energy corner state \(\left| {{A}_{\mathrm{cor}}} \right\rangle\), even in a set-up preserving both the full generalized chiral symmetry and the C3 symmetry40. Long-range hopping parameters in H″ between site A in the unit cell (m, n) and site B in the unit cell (m0, n0) are denoted with \(t_{ab}^{m,n;m_0,n_0}\) and equivalently for A–C coupling (Methods). We analytically find that the zero-energy state, residing solely on the A sublattice, can exist only if the following two conditions hold: \(t_{ac}^{m,n;m_0,n_0} = t_{ab}^{m,n;m_0 - 1,n_0 + 1}\) and \(t_{ac}^{m,n;m_0,n_0} = t_{ab}^{m,n;m_0,n_0}\) (Supplementary Section 6). These conditions are trivially satisfied if the long-range hopping is zero, that is, when the tight-binding approximation holds. Otherwise, they are too strict and unphysical as illustrated in Fig. 3b, as all coupling strengths between lattice sites indicated with solid lines must be equal.
However, as the coupling strength is typically correlated with the distance, an inspection of the A–B and A–C links in Fig. 3b and our theoretical analysis (Supplementary Section 6) suggest that, when t1 < t2, we should consider an approximate but more physical and less restrictive long-range hopping symmetry (LRHS):
Equation (4) implies that only those couplings indicated by the same colour in Fig. 3b must be equal. To test the protection of the corner state under the A-SubSy and LRHS, we calculate the spectra for a set of randomly chosen H′ + H″ perturbations of different magnitudes quantified by δ′ and δ″, respectively; these perturbations also retain the lattice symmetry by construction (Fig. 3e and Methods). We see that the zero-energy corner state remains in the gap and protected, until it is too close to the band at strong perturbations (this is a finite-size effect). The perturbed corner state is dominantly on the A sublattice as long as it is in the gap (Supplementary Section 7).
We experimentally test the protection of the corner state under the SubSy by implementing targeted next-nearest-neighbour hopping, introduced by imprinting bridge waveguides in the rhombic lattice (Methods). As shown in Fig. 4a (left), the lattice with B–B and C–C bridges preserves the A-SubSy, while the lattice in Fig. 4b (left) with A–A bridges breaks the A-SubSy. For the lattice with a broken A-SubSy, after excitation of the corner site on the A sublattice, there is light in the B and C waveguides nearest to the corner site (Fig. 4b, middle). This offers clear evidence that the corner mode is not protected anymore. On the contrary, for the lattice with a preserving A-SubSy, light is present solely on the A sublattice (Fig. 4a, middle), exhibiting the characteristics of HOTI corner states in BKLs20,21,39. This proves that the corner state, in this case, is protected against the B–B and C–C bridge perturbations. To underpin the experimental results, in Fig. 4a,b (right), we show results from numerical simulations obtained in realistic BKLs with parameters corresponding to those from the experiment, which display an excellent agreement. Long-distance simulations also validify that light remains localized at the corner without traversing through the bridges in Fig. 4a (left) due to topological protection but travels through the two bridges (even now they are further away) and spread into the bulk in Fig. 4b (left) (Supplementary Section 8).
a,b, Left: experimentally established A-SubSy-preserving lattice (with bridges connecting B–B and C–C sites; a), and A-SubSy-breaking lattice (with bridges connecting A–A sites; b). The white arrows mark that the corner lattice site is initially excited. Middle: three-dimensional intensity plots of the output probe beam after propagating through the A-SubSy-preserving lattice (a), where light is solely populating the A sublattice, and through the A-SubSy-breaking lattice (b), where the presence of light in B and C sublattice sites clearly indicates a destroyed topological corner mode. Right: numerically obtained intensity patterns corresponding to the experimental results in the middle panels, respectively. The white circles added to 2D intensity plots in the insets depict the corner structure of the BKL.
We are now ready to discuss our results with the focus on the diagram in Fig. 1. In the 1D SSH lattice, the left edge mode is protected by A-SubSy (encircled with a red line), while B-SubSy-preserving perturbations (encircled with a green line) do not affect the right edge mode. At the overlap region, one has the full chiral symmetry and the SPT phase. However, it has been shown that perturbations that respect the inversion symmetry (encircled with a grey line) protect the topological invariant, that is, the Zak phase, even if the full chiral symmetry is broken5,6.
Recently, it was argued that the SSH model is a poor TI44,45; more specifically, it is a band (Dirac) insulator featuring zero modes at a domain wall between two dimerizations arising from the Jackiw–Rebbi mechanism. Indeed, at low energy, in the long-wavelength limit, the tight-binding SSH model can be described by an effective 1D Dirac equation, where the Jackiw–Rebbi mechanism gives rise to a topological defect mode at zero energy44,45. Although we agree with this interpretation, the standardly used arguments for interpreting the SSH model as an SPT phase are holding (see, for example, refs. 2,46 and references therein and Supplementary Section 9). We emphasize that the intent of this paper is to accurately classify perturbations that destroy or protect the boundary states, where we use the SSH model as one of the examples to illustrate the suitability of the SubSy concept towards this goal.
The scenario in which BKLs are involved is more complex. First, we consider BKLs where long-range hopping is negligible, which is physically common when hopping is generated with evanescent coupling. The corner state on the A sublattice is robust with respect to A-SubSy-preserving perturbations and analogously for the corner states on other sublattices (their existence depends on the shape of the BKL flake). The topological invariant is quantized due to the C3 symmetry38. Thus, for a triangular flake of the BKL with C3 and generalized chiral symmetry, one can classify perturbations with respect to symmetries in accordance with Fig. 1 with an additional C-SubSy (not shown) and the grey encircled region corresponding to C3 symmetry. In this model, the BKL corner states are HOTI states.
When the long-range hopping beyond the neighbouring unit cells becomes appreciable, the protection of the corner state under A-SubSy and the LRHS can be interpreted as being inherited from the underlying Hamiltonian HK . This interpretation is underpinned by the calculation of the fractional corner anomaly (FCA)25 shown in Fig. 3f for an ensemble of randomly chosen A-SubSy- and LRHS-preserving perturbations. It is a clear signature of non-trivial topology and the existence of the corner state.
In conclusion, we have demonstrated SubSy-protected boundary states of SPT phases by employing perturbations that break the original topological invariants. Although the SubSy concept here arises from the chiral symmetries, we envision its applicability for other protecting symmetries as well. For the BKLs with non-negligible long-range hopping, we have unveiled a previously undiscovered LRHS that is essential for protection of the corner states, providing a basis for understanding their HOTI characteristics. We have used the 1D SSH and the BKL models to demonstrate our main findings. However, with appropriately defined SubSys, our findings can be applied to other systems, such as the 2D SSH lattice. More generally, our results extend beyond photonics to condensed-matter and cold atom systems, where many intriguing phenomena are mediated by the interplay of symmetry and topology. For example, a periodic zigzag SSH-like photonic lattice with A–A and B–B next-nearest-neighbour coupling (such as those in Fig. 2f,g (left)) can be engineered with Rydberg atoms47. Even though perturbations respecting or breaking SubSy are artificially engineered in our work, we nevertheless expect that such perturbations could naturally appear in a number of existing materials, including polymers or other organic and inorganic structures.
Methods
Projection operators
The projection operator PA is constructed by requiring that the amplitude of \(P_{\mathrm{A}}\left| \psi \right\rangle\) is identical to the amplitude of a given state \(\left| \psi \right\rangle\) on any A sublattice site and zero on any other sublattices. The other projection operators (PB, PC) are constructed fully analogously.
SSH lattice
The chiral symmetry of the SSH lattice in equation (1) implies that for every eigenstate \(\left| e \right\rangle\) satisfying \(H_{\mathrm{SSH}}\left| e \right\rangle = \beta \left| e \right\rangle\), there is another eigenstate \({{\varSigma }}_z\left| e \right\rangle\) with eigenvalue −β. This ensures that any perturbation of the Hamiltonian that preserves the chiral symmetry does not destroy the topologically protected edge states unless the gap closes and the system undergoes a topological phase transition to a trivial phase (for example, see ref. 2 and references therein).
Perturbations of the SSH model corresponding to A–B coupling are formally defined as \(H_{\mathrm{AB}} = \mathop {\varSigma}\nolimits_{m,n} {\left( {s_{ab}^{m,n}a_m^{\dagger} b_n + {\mathrm{h.c.}}} \right)}\), where am is the annihilation operator at an A sublattice site in the mth unit cell, and analogously for bn, while \(s_{ab}^{m,n}\) is the strength of the coupling. Similarly, \(H_{\mathrm{BB}} = \mathop {\varSigma}\nolimits_{m,n} {\left( {s_{bb}^{m,n}b_m^{\dagger} b_n + {\mathrm{h.c.}}} \right)}\), where m ≠ n, and analogously for HAA.
Breathing kagome lattice
The BKL Hamiltonian is given by
where \(a_{m,n}\) is the annihilation operator at an A sublattice site in the unit cell labelled with (m, n) indices and analogously for \(b_{m,n}\) and \(c_{m,n}\). All perturbations between sublattices A and B beyond the hopping corresponding to t1 and t2 can be described by
and analogously for HAC and HBC. The B–B hopping perturbations are described by
and analogously for HAA and HCC.
To construct perturbations, the hopping amplitudes between the unit cells \((m,n) \to (m \pm i,n \pm j)\), \(i,j = - 3, \ldots ,3\), are perturbed with strength \({\mathrm{rand}}\delta ^\prime |t_2 - t_1|\) for H′ = HBC + HBB + HCC and \({\mathrm{rand}} \delta ^{\prime\prime} |t_2 - t_1|\) for H″ = HAC + HAB. Here rand is a random number between 0 and 1 chosen with respect to uniform probability distribution. The nearest couplings t1 and t2 are not perturbed. The strength of the perturbations is given relative to the size of the gap, which is given by \(|t_2 - t_1|\). All perturbations retain the lattice symmetry. In Fig. 3c, for each magnitude of the perturbation δ′, we calculate and plot an ensemble of 70 spectra for randomly chosen H′. An equivalent procedure is used for Fig. 3e, where parameter δ″ is now varied, and δ′ = 0.05 is kept fixed. Every H″ respects the lattice symmetry, the A-SubSy, and the LRHS. The projections \(\left|\left\langle {{A}_{\mathrm{cor}}^\prime {{{\mathrm{|}}}}{{A}}_{\mathrm{cor}}} \right \rangle\right|^2\) and \(\left|\left \langle {{A}_{\mathrm{cor}}^\prime {{{\mathrm{|}}}}P_{\mathrm{A}}{{A}}_{\mathrm{cor}}^\prime } \right \rangle \right|^2\) between the unperturbed \(\left| {{A}_{\mathrm{cor}}} \right\rangle\) and the perturbed \(\left| {{A}_{\mathrm{cor}}^\prime } \right\rangle\) corner states are exactly unity for any H′ = HBB + HCC + HBC. However, for H′ + H″, \(\left|\left\langle {A_{\mathrm{cor}}^\prime {{{\mathrm{|}}}}A_{\mathrm{cor}}} \right \rangle \right|^2 < 1\) (Supplementary Section 7).
The FCA is calculated as (ρ − 2 σ) mod 1 following ref. 25; the red and black circles in Fig. 3f represent the mode density of the corner unit cell ρ and the average mode density of edge unit cells σ (with edges that intersect at the corner), respectively. The mode density is calculated as the local density of states integrated over all states above the bandgap in the propagation constant spectrum (shown in Fig. 3e).
Experimental set-up and methods
In our experiments, we establish the desired photonic lattices (either the 1D ‘twisted’ and zigzag SSH lattices shown in Fig. 2 or the two-dimensional rhombic kagome lattice as shown in Fig. 4) by site-to-site writing of waveguides in a strontium–barium niobate (SBN:61) photorefractive crystal with a continuous-wave laser19,39. As illustrated in Extended Data Fig. 1, a low-power laser beam featuring a 532 nm wavelength illuminates a spatial light modulator, which creates a quasi-non-diffracting writing beam with variable input positions onto the 20-mm-long biased crystal. The lattice-writing beam is ordinarily polarized, while the probe beam launched to the lattice edge is extraordinarily polarized. Because of the self-focusing nonlinearity and the photorefractive ‘memory’ effect19,39, all waveguides are induced and remain intact during the subsequent probing processes. Compared with the femtosecond laser-writing method largely employed in glass materials9,26, the photonic lattices in our crystal can be readily reconfigured from topological non-trivial to trivial structures simply by controlling the lattice spacing. After the multi-step writing process (with a bias field of 130 kV m−1) is completed, the whole lattice can be examined by sending a set of Gaussian beams into the crystal to probe the waveguides one by one, which leads to superimposed lattice structures shown in Figs. 2 and 4. To investigate the evolution of the topological states in this work, the probe beam used to excite the lattice edge/corner is set at a much weaker power of only about 20 nW, so it undergoes only linear propagation without nonlinear self-action through the lattice. (We note that the probe power can be increased to locally change the index structure of the lattices—the ingredient used for nonlinear control of topological states as in our previous work19,39.) The intensity patterns of the probe beam exiting the lattices (Figs. 2 and 4) are captured by an imaging lens paired to a charge-coupled device camera.
Data availability
Source data are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Chiu, C.-K. et al. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Longhi, S. Probing one-dimensional topological phases in waveguide lattices with broken chiral symmetry. Opt. Lett. 43, 4639–4642 (2018).
Jiao, Z. Q. et al. Experimentally detecting quantized Zak phases without chiral symmetry in photonic lattices. Phys. Rev. Lett. 127, 147401 (2021).
Poli, C. et al. Partial chiral symmetry-breaking as a route to spectrally isolated topological defect states in two-dimensional artificial materials. 2D Mater. 4, 025008 (2017).
Wang, Z. et al. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Hafezi, M. et al. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013).
Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).
Malkova, N. et al. Observation of optical Shockley-like surface states in photonic superlattices. Opt. Lett. 34, 1633–1635 (2009).
Keil, R. et al. The random mass Dirac model and long-range correlations on an integrated optical platform. Nat. Commun. 4, 1368 (2013).
Xiao, M., Zhang, Z. Q. & Chan, C. T. Surface impedance and bulk band geometric phases in one-dimensional systems. Phys. Rev. X 4, 021017 (2014).
Kruk, S. et al. Edge states and topological phase transitions in chains of dielectric nanoparticles. Small 13, 1603190 (2017).
Poddubny, A. et al. Topological Majorana states in zigzag chains of plasmonic nanoparticles. ACS Photon. 1, 101–105 (2014).
Blanco-Redondo, A. et al. Topological protection of biphoton states. Science 362, 568–571 (2018).
Weimann, S. et al. Topologically protected bound states in photonic parity-time-symmetric crystals. Nat. Mater. 16, 433–438 (2017).
Xia, S. et al. Nonlinear tuning of PT symmetry and non-Hermitian topological states. Science 372, 72–76 (2021).
Ni, X. et al. Observation of higher-order topological acoustic states protected by generalized chiral symmetry. Nat. Mater. 18, 113–120 (2019).
Xue, H. et al. Acoustic higher-order topological insulator on a Kagome lattice. Nat. Mater. 18, 108–112 (2019).
Li, M. et al. Higher-order topological states in photonic Kagome crystals with long-range interactions. Nat. Photon. 14, 89–94 (2019).
El Hassan, A. et al. Corner states of light in photonic waveguides. Nat. Photon. 13, 697–700 (2019).
Kempkes, S. N. et al. Robust zero-energy modes in an electronic higher-order topological insulator. Nat. Mater. 18, 1292–1297 (2019).
Peterson Christopher, W. et al. A fractional corner anomaly reveals higher-order topology. Science 368, 1114–1118 (2020).
Kirsch, M. S. et al. Nonlinear second-order photonic topological insulators. Nat. Phys. 17, 995–1000 (2021).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).
Song, Z., Fang, Z. & Fang, C. (d-2)-dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 119, 246402 (2017).
Langbehn, J. et al. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 119, 246401 (2017).
Schindler, F. et al. Higher-order topology in bismuth. Nat. Phys. 14, 918–924 (2018).
Noh, J. et al. Topological protection of photonic mid-gap defect modes. Nat. Photon. 12, 408–415 (2018).
Imhof, S. et al. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 14, 925–929 (2018).
Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342–345 (2018).
Mittal, S. et al. Photonic quadrupole topological phases. Nat. Photon. 13, 692–696 (2019).
Zhang, X. et al. Second-order topology and multidimensional topological transitions in sonic crystals. Nat. Phys. 15, 582–588 (2019).
Xie, B. Y. et al. Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals. Phys. Rev. Lett. 122, 233903 (2019).
Chen, X. D. et al. Direct observation of corner states in second-order topological photonic crystal slabs. Phys. Rev. Lett. 122, 233902 (2019).
Benalcazar, W. A., Li, T. & Hughes, T. L. Quantization of fractional corner charge in Cn-symmetric higher-order topological crystalline insulators. Phys. Rev. B 99, 245151 (2019).
Hu, Z. et al. Nonlinear control of photonic higher-order topological bound states in the continuum. Light. Sci. Appl. 10, 164 (2021).
Van Miert, G. & Ortix, C. On the topological immunity of corner states in two-dimensional crystalline insulators. npj Quantum Mater. 5, 63 (2020).
Jung, M., Yu, Y. & Shvets, G. Exact higher-order bulk–boundary correspondence of corner-localized states. Phys. Rev. B 104, 195437 (2021).
Herrera, M. A. J. et al. Corner modes of the breathing kagome lattice: origin and robustness. Phys. Rev. B 105, 085411 (2022).
Hsu, C. W. et al. Bound states in the continuum. Nat. Rev. Mater. 1, 16048 (2016).
Fuchs, J.-N. & Piéchon, F. Orbital embedding and topology of one-dimensional two-band insulators. Phys. Rev. B 104, 235428 (2021).
Cayssol, J. & Fuchs, J. N. Topological and geometrical aspects of band theory. J. Phys. Mater. 4, 034007 (2021).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 96, 245115 (2017).
de Leseleuc, S. et al. Observation of a symmetry-protected topological phase of interacting bosons with Rydberg atoms. Science 365, 775–780 (2019).
Acknowledgements
We acknowledge assistance from R. Cheng and Y. Wang. This research is supported by the National Key R&D Program of China under grant no. 2022YFA1404800, the National Natural Science Foundation (12134006, 12274242) and the QuantiXLie Center of Excellence, a project co-financed by the Croatian Government and European Union through the European Regional Development Fund—the Competitiveness and Cohesion Operational Programme (grant KK.01.1.1.01.0004). D.B. acknowledges support from the 66 Postdoctoral Science Grant of China and the National Natural Science Foundation (12250410236). R.M. acknowledges support from NSERC and the CRC programme in Canada.
Author information
Authors and Affiliations
Contributions
Z.H., D.B. and X.W. realized the photonic lattices and performed the experiments. Z.W., X.W., D.J. and H.B. performed theoretical analysis and numerical simulations of the discrete models. D.B. and Z.H. performed numerical simulations of the continuous models. H.B., Z.C. and R.M. supervised the work. All the authors discussed the results and contributed to this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Ioannis Petrides and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Schematic illustration of the experimental setup employed for writing and probing a photonic lattice in a photorefractive crystal.
CW: the continuous-wave laser beam; SLM: spatial light modulator; BS: beam splitter; FM: Fourier mask; L: circular lens; SBN: strontium barium niobite crystal; M: mirror; λ/2: half-wavelength plate; CCD: charge-coupled device. The inset shows a laser-written “bridged” kagome lattice used in the experimental work of Fig. 4. The bottom path is used as a reference beam for interference measurement when needed.
Supplementary information
Supplementary Information
Supplementary Figs. 1–7 and Discussion.
Source data
Source Data Fig. 2
Numerically calculated data.
Source Data Fig. 3
Numerically calculated data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Z., Wang, X., Hu, Z. et al. Sub-symmetry-protected topological states. Nat. Phys. 19, 992–998 (2023). https://doi.org/10.1038/s41567-023-02011-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-023-02011-9
This article is cited by
-
Quantized polarization and Majorana fermions beyond tenfold classification
Communications Physics (2024)
-
Information-entropy enabled identifying topological photonic phase in real space
Frontiers of Optoelectronics (2024)