Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Signature of collective elastic glass physics in surface-induced long-range tails in dynamical gradients

Nature Physics volume 19, pages 800–806 (2023)Cite this article

Subjects

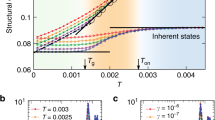
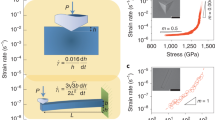
Abstract

Understanding the underlying nature of dynamical correlations believed to drive the bulk glass transition is a long-standing problem. Here we show that the form of spatial gradients of the glass transition temperature and structural relaxation time near an interface indeed provide signatures of the nature of relaxation in bulk glass-forming liquids. We report the results of long-time, large-system molecular dynamics simulations of thick glass-forming polymer films with one vapour interface, supported on a dynamically neutral substrate. We find that gradients in the glass transition temperature and logarithm of the structural relaxation time nucleated at a vapour interface exhibit two distinct regimes: a medium-ranged, large-amplitude exponential gradient, followed by a long-range slowly decaying tail that can be described by an inverse power law. This behaviour disagrees with multiple proposed theories of glassy dynamics but is predicted by the ‘elastically collective nonlinear Langevin equation’ theory as a consequence of two coupled mechanisms: a medium-ranged interface-nucleated gradient of surface-modified local caging constraints, and an interfacial truncation of a long-ranged collective elastic field. These findings support a coupled spatially local–nonlocal mechanism of activated glassy relaxation and kinetic vitrification in both the isotropic bulk and in broken-symmetry films.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Simulation and theory of normalized dynamical gradients of the shift of the glass transition temperature and alpha relaxation time relative to the bulk.
Fig. 2: Schematic of the film and key concepts of ECNLE theory, where ‘layers’ are shown only for illustrative reasons and density is homogeneous in all directions within the film.
Fig. 3: Theoretical predictions for the fractional and normalized deviations from bulk of multiple dynamical properties as a function of distance from the vapour interface.

Similar content being viewed by others

Data availability

All relevant data are included in the paper and/or its Supplementary Information files. Raw simulation trajectory files, which are prohibitively large, are available upon reasonable request from D.S.S.

Code availability

All results in this paper employed openly available codes and/or standard numerical algorithms.

References

  1. Cavagna, A. Supercooled liquids for pedestrians. Phys. Rep. 476, 51–124 (2009).

    Article  ADS  Google Scholar 

  2. Debenedetti, P. G. & Stillinger, F. H. Supercooled liquids and the glass transition. Nature 410, 259–267 (2001).

    Article  ADS  Google Scholar 

  3. Angell, C. A. Formation of glasses from liquids and biopolymers. Science 267, 1924–1935 (1995).

    Article  ADS  Google Scholar 

  4. Adam, G. & Gibbs, J. H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 43, 139–146 (1965).

    Article  ADS  Google Scholar 

  5. Kirkpatrick, T. R., Thirumalai, D. & Wolynes, P. G. Scaling concepts for the dynamics of viscous liquids near an ideal glassy state. Phys. Rev. A 40, 1045–1054 (1989).

    Article  ADS  Google Scholar 

  6. Lubchenko, V. & Wolynes, P. G. Theory of structural glasses and supercooled liquids. Annu. Rev. Phys. Chem. 58, 235–266 (2007).

    Article  ADS  Google Scholar 

  7. White, R. P. & Lipson, J. E. Polymer free volume and its connection to the glass transition. Macromolecules 49, 3987–4007 (2016).

    Article  ADS  Google Scholar 

  8. Long, D. & Lequeux, F. Heterogeneous dynamics at the glass transition in van der Waals liquids, in the bulk and in thin films. Eur. Phys. J. E 4, 371–387 (2001).

    Article  Google Scholar 

  9. Chandler, D. & Garrahan, J. P. Dynamics on the way to forming glass: bubbles in space-time. Annu. Rev. Phys. Chem. 61, 191–217 (2010).

    Article  Google Scholar 

  10. Dyre, J. C. Colloquium: the glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 78, 953–972 (2006).

    Article  ADS  Google Scholar 

  11. Hall, R. W. & Wolynes, P. G. The aperiodic crystal picture and free-energy barriers in glasses. J. Chem. Phys. 86, 2943–2948 (1987).

    Article  ADS  Google Scholar 

  12. Mirigian, S. & Schweizer, K. S. Elastically cooperative activated barrier hopping theory of relaxation in viscous fluids. I. General formulation and application to hard sphere fluids. J. Chem. Phys. 140, 194506 (2014).

    Article  ADS  Google Scholar 

  13. Mirigian, S. & Schweizer, K. S. Elastically cooperative activated barrier hopping theory of relaxation in viscous fluids. II. Thermal liquids. J. Chem. Phys. 140, 194507 (2014).

    Article  ADS  Google Scholar 

  14. Forrest, J. A. & Dalnoki-Veress, K. The glass transition in thin polymer films. Adv. Colloid Interface Sci. 94, 167–195 (2001).

    Article  Google Scholar 

  15. Alcoutlabi, M. & McKenna, G. B. Effects of confinement on material behaviour at the nanometre size scale. J. Phys. Condens. Matter 17, R461–R524 (2005).

    Article  ADS  Google Scholar 

  16. Baschnagel, J. & Varnik, F. Computer simulations of supercooled polymer melts in the bulk and in confined geometry. J. Phys. Condens. Matter 17, R851–R953 (2005).

    Article  ADS  Google Scholar 

  17. Ediger, M. D. & Forrest, J. A. Dynamics near free surfaces and the glass transition in thin polymer films: a view to the future. Macromolecules 47, 471–478 (2014).

    Article  ADS  Google Scholar 

  18. Li, Y. et al. Surface diffusion in glasses of rod-like molecules posaconazole and itraconazole: effect of interfacial molecular alignment and bulk penetration. Soft Matter 16, 5062–5070 (2020).

    Article  ADS  Google Scholar 

  19. Ediger, M. D. Perspective. Highly stable vapor-deposited glasses. J. Chem. Phys. 147, 210901 (2017).

    Article  ADS  Google Scholar 

  20. Simmons, D. S. An Emerging unified view of dynamic interphases in polymers. Macromol. Chem. Phys. 217, 137–148 (2016).

    Article  Google Scholar 

  21. Keddie, J. L., Jones, R. A. L. & Cory, R. A. Size-dependent depression of the glass transition temperature in polymer films. Europhys. Lett. 27, 59–64 (1994).

    Article  ADS  Google Scholar 

  22. Jancar, J. et al. Current issues in research on structure-property relationships in polymer nanocomposites. Polymer 51, 3321–3343 (2010).

    Article  Google Scholar 

  23. Christie, D., Register, R. A. & Priestley, R. D. Direct measurement of the local glass transition in self-assembled copolymers with nanometer resolution. ACS Cent. Sci. 4, 504–511 (2018).

    Article  Google Scholar 

  24. Wunderlich, B. Reversible crystallization and the rigid-amorphous phase in semicrystalline macromolecules. Prog. Polym. Sci. 28, 383–450 (2003).

    Article  Google Scholar 

  25. Jackson, C. L. & McKenna, G. B. The glass transition of organic liquids confined to small pores. J. Non-Cryst. Solids 131-133, 221–224 (1991).

    Article  ADS  Google Scholar 

  26. Schweizer, K. S. & Simmons, D. S. Progress towards a phenomenological picture and theoretical understanding of glassy dynamics and vitrification near interfaces and under nanoconfinement. J. Chem. Phys. 151, 240901 (2019).

    Article  ADS  Google Scholar 

  27. Richert, R. Dynamics of nanoconfined supercooled liquids. Annu. Rev. Phys. Chem. 62, 65–84 (2011).

    Article  ADS  Google Scholar 

  28. Napolitano, S., Glynos, E. & Tito, N. B. Glass transition of polymers in bulk, confined geometries and near interfaces. Rep. Prog. Phys. 80, 036602 (2017).

    Article  ADS  Google Scholar 

  29. Stevenson, J. D. & Wolynes, P. G. On the surface of glasses. J. Chem. Phys. 129, 234514 (2008).

    Article  ADS  Google Scholar 

  30. Merabia, S., Sotta, P. & Long, D. Heterogeneous nature of the dynamics and glass transition in thin polymer films. Eur. Phys. J. E 15, 189–210 (2004).

    Article  Google Scholar 

  31. White, R. P. & Lipson, J. E. G. Dynamics across a free surface reflect interplay between density and cooperative length: application to polystyrene. Macromolecules 54, 4136–4144 (2021).

    Article  ADS  Google Scholar 

  32. Salez, T., Salez, J., Dalnoki-Veress, K., Raphaël, E. & Forrest, J. A. Cooperative strings and glassy interfaces. Proc. Natl Acad. Sci. USA 112, 8227 (2015).

    Article  ADS  Google Scholar 

  33. Phan, A. D. & Schweizer, K. S. Influence of longer range transfer of vapor interface modified caging constraints on the spatially heterogeneous dynamics of glass-forming liquids. Macromolecules 52, 5192–5206 (2019).

    Article  ADS  Google Scholar 

  34. Mangalara, J. H., Marvin, M. D., Wiener, N. R., Mackura, M. E. & Simmons, D. S. Does fragility of glass formation determine the strength of Tg-nanoconfinement effects? J. Chem. Phys. 146, 104902 (2017).

    Article  ADS  Google Scholar 

  35. Hanakata, P. Z., Douglas, J. F. & Starr, F. W. Local variation of fragility and glass transition temperature of ultra-thin supported polymer films. J. Chem. Phys. 137, 244901 (2012).

    Article  ADS  Google Scholar 

  36. Zhou, Y. & Milner, S. T. Short-time dynamics reveals Tg suppression in simulated polystyrene thin films. Macromolecules 50, 5599–5610 (2017).

    Article  ADS  Google Scholar 

  37. Diaz-Vela, D., Hung, J.-H. & Simmons, D. S. Temperature-independent rescaling of the local activation barrier drives free surface nanoconfinement effects on segmental-scale translational dynamics near Tg. ACS Macro Lett 7, 1295–1301 (2018).

    Article  Google Scholar 

  38. Scheidler, P., Kob, W. & Binder, K. Cooperative motion and growing length scales in supercooled confined liquids. Europhys. Lett. 59, 701–707 (2002).

    Article  ADS  Google Scholar 

  39. Ghanekarade, A., Phan, A. D., Schweizer, K. S. & Simmons, D. S. Nature of dynamic gradients, glass formation and collective effects in ultrathin freestanding films. Proc. Natl Acad. Sci. USA 118, e2104398118 (2021).

    Article  Google Scholar 

  40. Schmidtke, B., Hofmann, M., Lichtinger, A. & Rössler, E. A. Temperature dependence of the segmental relaxation time of polymers revisited. Macromolecules 48, 3005–3013 (2015).

    Article  ADS  Google Scholar 

  41. Kob, W., Roldán-Vargas, S. & Berthier, L. Non-monotonic temperature evolution of dynamic correlations in glass-forming liquids. Nat. Phys. 8, 164–167 (2012).

    Article  Google Scholar 

  42. Hocky, G. M., Berthier, L., Kob, W. & Reichman, D. R. Crossovers in the dynamics of supercooled liquids probed by an amorphous wall. Phys. Rev. E 89, 052311 (2014).

    Article  ADS  Google Scholar 

  43. Mirigian, S. & Schweizer, K. S. Dynamical theory of segmental relaxation and emergent elasticity in supercooled polymer melts. Macromolecules 48, 1901–1913 (2015).

    Article  ADS  Google Scholar 

  44. Phan, A. D. & Schweizer, K. S. Theory of the spatial transfer of interface-nucleated changes of dynamical constraints and its consequences in glass-forming films. J. Chem. Phys. 150, 044508 (2019).

    Article  ADS  Google Scholar 

  45. White, R. P. & Lipson, J. E. G. To understand film dynamics look to the bulk. Phys. Rev. Lett. 125, 058002 (2020).

    Article  ADS  Google Scholar 

  46. Napolitano, S. & Wübbenhorst, M. Structural relaxation and dynamic fragility of freely standing polymer films. Polymer 51, 5309–5312 (2010).

    Article  Google Scholar 

  47. Paeng, K., Swallen, S. F. & Ediger, M. D. Direct measurement of molecular motion in freestanding polystyrene thin films. J. Am. Chem. Soc. 133, 8444–8447 (2011).

    Article  Google Scholar 

  48. Mirigian, S. & Schweizer, K. S. Theory of activated glassy relaxation, mobility gradients, surface diffusion and vitrification in free standing thin films. J. Chem. Phys. 143, 244705 (2015).

    Article  ADS  Google Scholar 

  49. Chowdhury, M. et al. Spatially distributed rheological properties in confined polymers by noncontact shear. J. Phys. Chem. Lett. 8, 1229–1234 (2017).

    Article  Google Scholar 

  50. Hao, Z. et al. Mobility gradients yield rubbery surfaces on top of polymer glasses. Nature 596, 372–376 (2021).

    Article  ADS  Google Scholar 

  51. Xie, S.-J. & Schweizer, K. S. A collective elastic fluctuation mechanism for decoupling and stretched relaxation in glassy colloidal and molecular liquids. J. Chem. Phys. 152, 034502 (2020).

    Article  ADS  Google Scholar 

  52. Li, Y. et al. Surface diffusion is controlled by bulk fragility across all glass types. Phys. Rev. Lett. 128, 075501 (2022).

    Article  ADS  Google Scholar 

  53. Evans, C. M., Deng, H., Jager, W. F. & Torkelson, J. M. Fragility is a key parameter in determining the magnitude of Tg-confinement effects in polymer films. Macromolecules 46, 6091–6103 (2013).

    Article  ADS  Google Scholar 

  54. Baglay, R. R. & Roth, C. B. Communication: experimentally determined profile of local glass transition temperature across a glassy-rubbery polymer interface with a Tg difference of 80 K. J. Chem. Phys. 143, 111101 (2015).

    Article  ADS  Google Scholar 

  55. Huang, X. & Roth, C. B. Optimizing the grafting density of tethered chains to alter the local glass transition temperature of polystyrene near silica substrates: the advantage of mushrooms over brushes. ACS Macro Lett. 7, 269–274 (2018).

    Article  Google Scholar 

  56. Mei, B., Zhou, Y. & Schweizer, K. S. Experimental test of a predicted dynamics-structure-thermodynamics connection in molecularly complex glass-forming liquids. Proc. Natl Acad. Sci. USA 118, e2025341118 (2021).

    Article  Google Scholar 

  57. Grest, G. & Kremer, K. Molecular-dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 33, 3628–3631 (1986).

    Article  ADS  Google Scholar 

  58. Mackura, M. E. & Simmons, D. S. Enhancing heterogenous crystallization resistance in a bead-spring polymer model by modifying bond length. J. Polym. Sci. B Polym. Phys. 52, 134–140 (2014).

    Article  ADS  Google Scholar 

  59. Ivancic, R. J. S. & Riggleman, R. A. Dynamic phase transitions in freestanding polymer thin films. Proc. Natl Acad. Sci. USA 117, 25407–25413 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  60. Vogel, H. Das temperatur-Abhängigkeitsgesetz der Viskosität von Flüssigkeiten. Phys. Zeit 22, 645–646 (1921).

    Google Scholar 

  61. Fulcher, G. S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 8, 339–355 (1925).

    Google Scholar 

Download references

Acknowledgements

D.S.S. and A.G. have been supported by the National Science Foundation (NSF) CAREER Award under grant no. DMR-1849594.

Author information

Authors and Affiliations

  1. Department of Chemical, Biological and Materials Engineering, University of South Florida, Tampa, FL, USA

    Asieh Ghanekarade & David S. Simmons

  2. Faculty of Materials Science and Engineering, Phenikaa University, Hanoi, Vietnam

    Anh D. Phan

  3. Departments of Materials Science and Chemistry and Materials Research Laboratory, University of Illinois, Urbana, IL, USA

    Kenneth S. Schweizer

Authors
  1. Asieh Ghanekarade
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Anh D. Phan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kenneth S. Schweizer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. David S. Simmons
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The paper and Supplementary Information were written based on the contributions of all authors. A.G. performed all simulations under the supervision of D.S.S. A.G. and D.S.S. jointly conceived of and analysed all simulations. A.D.P. and K.S.S. performed all ECNLE theory analytical analysis and numerical calculations.

Corresponding authors

Correspondence to Anh D. Phan, Kenneth S. Schweizer or David S. Simmons.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Detailed simulation methods, Supplementary Figs. 1–6 and theory details.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghanekarade, A., Phan, A.D., Schweizer, K.S. et al. Signature of collective elastic glass physics in surface-induced long-range tails in dynamical gradients. Nat. Phys. 19, 800–806 (2023). https://doi.org/10.1038/s41567-023-01995-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-023-01995-8

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing