Fish shoals resemble a stochastic excitable system driven by environmental perturbations

Abstract

Groups of animals can perform highly coordinated collective behaviours that confer benefits to the participating individuals by facilitating social information exchange and protection from predators¹. Some of these characteristics could arise when groups operate at critical points between two structurally and functionally different states, leading to maximal responsiveness to external stimuli and effective propagation of information^2,3. It has been proposed that animal groups constitute examples of self-organized systems at criticality^2,3; however, direct empirical evidence of this hypothesis—in particular in the wild—is mostly absent. Here we show that highly conspicuous, repetitive and rhythmic collective dive cascades produced by many thousands of freshwater fish under high predation risk resemble a stochastic excitable system driven by environmental perturbations. Together with the results of an agent-based model of the system, this suggests that these fish shoals might operate at a critical point between a state of high individual diving activity and low overall diving activity. We show that the best fitting model, which is located at a critical point, allows information about external perturbations—such as predator attacks—to propagate most effectively through the shoal. Our results suggest that criticality might be a plausible principle of distributed information processing in large animal collectives.

Main

Collective systems in biology—such as neuronal networks or large animal groups—are able to perform efficient collective information processing, although each unit or agent often only has access to local information¹. It has been proposed that this feature of collective biological systems is due to systems operating at the boundary between dynamical regimes of different types, at critical points. At such critical points, the system’s macroscopic behaviour undergoes a qualitative change—that is, a phase transition^4,2—and the system as a whole becomes highly sensitive to external perturbations, facilitating efficient collective information processing^2,5,6. Critical or slightly sub-critical behaviour has been reported for neuronal systems^{5,7,8,9,10,11,12,13}, but evidence for (near)-criticality in other collective information-processing systems, including animal groups, remains sparse^2,4,14. In addition, studies of collective behaviour of animal groups under natural conditions beyond a few hundreds of individuals and over extended periods of time beyond a few seconds^4,15 are missing. In this Letter we address this important gap by observing large groups of fish comprising hundreds of thousands of individuals¹⁶ over hours and in their natural ecosystem. By analysing this unique dataset, we provide evidence that giant fish shoals under high predation risk resemble a stochastic excitable system driven by environmental perturbations. By combining these empirical observations with computational modelling, we suggest that the fish system appears to operate close to criticality and that this could result in a near-optimal propagation of environmental cues, something that would confer benefits at the individual level in the corresponding ecosystem.

Our results are based on an investigation of the collective diving behaviour of sulphur molly (Poecilia sulphuraria) shoals. These fish are endemic to a sulfidic stream system near the city of Teapa in southern Mexico^16,17 (Fig. 1a and Methods). Among several adaptations to toxic concentrations of hydrogen sulfide (H₂S) as well as hypoxic conditions in their habitats^17,18,19,20, these fish spend substantial parts of their time at the water surface, using the thin but oxygen-rich air–water interface to perform aquatic surface respiration^21,22 (Supplementary Video 1). Typically, these fish aggregate in quasi-two-dimensional (2D) shoals of up to 3,000 individuals per square metre at the surface¹⁶, which suggests that the area covered in our recordings contained several hundred thousands of individuals. These surface-dwelling, high-density fish shoals attract various bird species as aerial predators at high frequencies^16,22,23, and fish react to the attacking birds by exhibiting a highly synchronized collective diving behaviour. As the fish touch the water surface with their tails when initiating a dive, a characteristic and easily traceable water disturbance (visual splash—a wave) may spread through the shoal in an avalanche-like manner^16,24 that resembles the ‘Mexican waves’ observed in football stadiums²⁵. These large-scale repeated waves that appear after bird attacks function as a deterrent behaviour that leads to fewer and less successful attacks by birds¹⁶.

Fig. 1: Analysis of empirical data of the surface-wave activity.

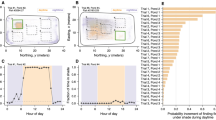
a, Localization of the field site in Teapa, Tabasco. The main pond, where all the videos were taken, is marked in the inset of the map. b, Snapshots of the rectification and background subtraction processes performed on the empirical videos. Active pixels caused by the disturbance of the surface as fish dive down are depicted in white. c, Plot of one surface-activity signal ${{{\mathcal{A}}}}{(t)}$ that is representative for all empirical videos. The inset serves to visualize the inter-spike time τ₁ and the spike-duration time τ₂. d,e, Plots of the distributions of the characteristic times P(τ₁) (d) and P(τ₂) (e) obtained from the empirical data. Both distributions are consistent with gamma distributions, which have exponentially decaying tails (KS statistic, p = 0.013 and p = 0.034, respectively), shown as black dashed lines. f, Plot of the distribution of the cluster areas P(a) obtained from the empirical data. The power-law fit (black dashed line) was estimated following ref. ³⁰ (KS statistic, p = 0.044). For spatial scales ranging from 10⁻¹ m² up to 10² m², the exponent is found to be α_a ≈ 2.3. See Methods for details on the goodness-of-fit for all empirical distributions.

A key observation is that the synchronized collective diving behaviour, hereafter referred to as ‘surface-wave activity’, also occurs spontaneously in the absence of bird attacks, as seen in Supplementary Video 2. This spontaneous and stochastic surface-wave activity may be viewed as analogous to the resting-state activity in neuronal systems^26,27. The system thus provides an optimal set-up for empirically testing the criticality hypothesis and investigating the benefits and potential trade-offs of critical behaviour in the wild²⁸. Due to the high predatory bird activity in the system^22,24, we hypothesized that these fish shoals would probably benefit from being in a constant state of alertness, operating at a critical point between two phases, one of low and another of high surface-wave activity. If so, the prediction would be to find intermittent surface-wave activity that can propagate through the whole system, giving rise to waves of different sizes ranging from small ones, involving a few individuals, to large ones involving most individuals in the shoals, which would follow a power-law distribution.

To test this hypothesis, we acquired videos, over multiple days, of the spontaneous and stochastic surface-wave activity in the absence of bird attacks, driven only by small-scale perturbations induced by external factors or uncertainty in individual perception (refs. ^{22 and 24} and Methods). Using a custom computer vision processing pipeline, we binarized the original videos into ‘active’ pixels that represent the diving of fish (state ${{{\mathcal{D}}}}$) and ‘non-active’ pixels corresponding to fish during surface and underwater states ${{{\mathcal{S}}}}$ and ${{{\mathcal{U}}}}$ (see Fig. 1b and Methods for details). An example of the resulting processed videos is provided as Supplementary Video 3.

We first analysed the empirical surface-activity signal ${{{\mathcal{A}}}}{(t)}$, defined as the fraction of active pixels in the video, as a proxy for the number of fish diving at a given moment in time. We observed peaks of activity (‘spikes’), corresponding to waves spreading through the system, separated by long periods of low activity corresponding to small-scale, non-propagating surface activity (Fig. 1c, inset). Both the probability distribution of inter-spike time intervals τ₁ and the probability distribution of spike-duration times τ₂ have exponentially decaying tails (Fig. 1d,e and Extended Data Fig. 1). The mean time interval between spikes was significantly longer than their duration (〈τ₁〉 = 12.84 ± 8.35 s and 〈τ₂〉 = 0.68 ± 0.41 s, Wilcoxon one-sided signed-rank test, W = 1,523,502.5, p < 0.001), indicating that the propagation time of the waves is much smaller than the time between successive waves.

In a second step, we analysed how single waves spread through the shoals. To this end, we defined activity clusters as the number of active pixels connected in time and space corresponding to a single wave (as defined in ref. ²⁹; see Methods for details). We found that the empirical cluster size distribution is consistent with a power-law distribution with an exponent of α_a = 2.3 (Kolmogorov–Smirnov (KS) statistic³⁰, p = 0.044; Fig. 1f and Extended Data Fig. 2). This exponent is robust across several decades, ranging from 10⁻¹ m² to 10² m². The existence of a wave size distribution that is consistent with a power law suggests that the system operates at criticality¹².

However, a power-law distribution in empirical data is not sufficient, alone, to conclude that a system is at criticality¹². Thus, to provide further evidence that the observed surface-wave activity is at the edge between two different dynamical regimes, we devised a generic model for the spatiotemporal propagation of the surface-activity waves. In this way we can simulate the emergent collective dynamics and identify parameters best fitting the observed macroscopic behaviour. Our prediction here is that if the fish shoals are operating at a critical point, we will find that the parameters that best fit the data are indeed located at a phase transition (critical point). One way to quantify this is to calculate the average correlation of fluctuations between neighbouring cells, which peaks at the phase transition^6,12.

We modelled the spontaneous surface-wave activity in a similar manner to Farkas and others²⁵. The surface is subdivided into spatial cells, each representing the mean dynamics of a subset of fish. Each cell can be in one of three states, corresponding to the stereotypical behaviours ${{{\mathcal{S}}}}$ (surface), ${{{\mathcal{D}}}}$ (dive) or ${{{\mathcal{U}}}}$ (underwater), as seen in the scheme in Fig. 2a. Cells enter the diving state stochastically, either spontaneously by environmental noise or driven by neighbouring cells³¹, making the propagation of diving events possible. The model has five free parameters: two time constants that control how long the cells remain in the diving and underwater state, two parameters that control the stochasticity of spontaneous events (parameters ω and μ) and—crucially—a coupling parameter θ, which represents an activation threshold and controls how many neighbouring cells need to be activated to prompt a given cell to become active. We first matched the time constants to previously published experimental data¹⁶ before performing a systematic parameter search to identify the values ω^⋆, θ^⋆ and μ^⋆ that best fit the surface-wave activity of the empirical system (Extended Data Fig. 3). The fit optimized two quantities, one quantifying the temporal dynamics of the system and one characterizing the local spatial dynamics (see Methods and Extended Data Figs. 4 and 5 for details). The best fitting model reproduces the empirical data, both qualitatively (snapshots of the dynamics and surface-activity signal are shown in Fig. 2b,c, respectively) and quantitatively in terms of the distributions of the characteristic times P(τ₁) and P(τ₂) (Fig. 2d,e), as well as the cluster size distribution P(a) (Fig. 2f). We note that in the analysis of the simulation results we used time series of the same length as were available from experiments (Methods). Thus, the exponential tails in the inter-spike distributions are probably induced by the relatively short observation windows due to experimental constraints.

Fig. 2: Computational model of surface activity.

a, We categorized the behaviour of individual fish into three fundamental states: swimming near the surface for respiration (${{{\mathcal{S}}}}$), fast diving (${{{\mathcal{D}}}}$) and underwater hovering with subsequent slow resurfacing (${{{\mathcal{U}}}}$)²⁴. b, Comparison between snapshots obtained from the empirical videos and the numerical simulations. c, Surface-activity signal ${{{\mathcal{A}}}}{(t)}$ computed using the model shown in a. d,e, Characteristic time distributions for the inter-spike times τ₁ (d) and the spike-duration times τ₂ (e). f, Distribution of cluster areas P(a), which is statistically consistent with a power law (black dashed line) with exponent α_a = 2.3. g, Plots of the surface-activity signal ${{{\mathcal{A}}}}{(t)}$ for three different sets of parameters, highlighted with different markers in h. h, Average neighbour correlation function ${\langle c(\omega ,\,\theta ,\,{\mu }^{\star })\rangle }_{t}$ showing a maximum at the critical region. The blue cross indicates the location of (ω^⋆, θ^⋆). i, Plots of ${\langle c({\omega }^{\star },\,\theta ,\,{\mu }^{\star })\rangle }_{t}$ and ${\langle c(\omega ,\,{\theta }^{\star },\,{\mu }^{\star })\rangle }_{t}$ to visualize the maximum when changing variables θ and ω. The plots in b–f were generated using numerical simulations and the parameters ω^⋆, θ^⋆ and μ^⋆. For details, see the section Model implementation in Methods.

By varying the spontaneous and coupling parameters ω and θ while fixing the other parameters to their best fitting values, we find that the ones that best fit the data are indeed located at a phase transition (critical point), where the system behaviour undergoes a fundamental change mainly with respect to variations in the coupling parameter θ. For stronger coupling (lower θ), the system exhibits high levels of persistent activity, effectively spanning the whole system. For weaker coupling (higher θ), we observe only small non-propagating, purely noise-driven activations (Fig. 2g and Supplementary Video 4). As predicted, the model shows a maximal average correlation at a specific value of the coupling parameter θ and remains largely unaffected by the spontaneous transition rate ω, as seen in Fig. 2h–i (see Methods for details). This means that variation of the social interactions among individuals is responsible for moving the system across the activity phases. To further support that the observed transition in the computational model is indeed a critical one, we computed the susceptibility of the surface-activity signal ${{{\mathcal{A}}}}{(t)}$ as a function of system size (L ∈ [25, 50, 100, 200, 400, 800]). We found that the susceptibility increases as a function of system size in a way that is consistent with a power law with exponent ≈ 1.7 (Extended Data Fig. 6). As a complement to this numerical analysis of the critical transition in the model, we computed the susceptibility in the empirical videos using different window sizes. We found that, in the empirical data, the susceptibility of the activity also increases with increasing window size (Extended Data Fig. 7). The exponents vary across measurement days—potentially due to environmental factors such as temperature, or lighting conditions—but they are consistent with the exponent in the model for at least three measurement days. Thus, the combination of these numerical and empirical results suggests that the system operates in close vicinity to a critical point. Details on the analysis of the critical transition are provided in Methods (see section Analysis of the critical transition).

To investigate the possibility that the individual fish in shoals at the critical point could benefit from optimal sensitivity to environmental stimuli³², as well as efficient information propagation across large distances³³, we combined two different computational approaches. First, using the numerical model, we tested the sensitivity of the system when exposed to external perturbations of different intensities, analogous to ref. ³⁴. At random points in time we activated a number ${{{\mathcal{I}}}}$ of cells in a perturbation zone (PZ in Fig. 3a) always located in the centre of the system, and observed its response in a sampling zone (SZ in Fig. 3a), which consisted of a larger set of cells excluding the cells of the PZ. The sizes of the PZ and SZ were selected such that the size of the SZ is one order of magnitude larger than the PZ. We characterized the ability of the system to detect a perturbation of a given intensity ${{{\mathcal{I}}}}$ by calculating the surface-activity signal of the cells in the SZ (${{{{\mathcal{A}}}}}_{\rm{SZ}}{(t)}$) and then computing its time average. We then implemented receiver operating characteristic (ROC) analysis to quantify the effect of the perturbations on the system. To obtain a binary classification, we implemented numerical simulations with no perturbation (true negative (TN) case) and compared them with simulations perturbed with the five different intensities (true positive (TP) cases). For each perturbation intensity ${{{\mathcal{I}}}}$, we computed the area under the curve (AUC) of the false positive (FP) versus TP curve. We found that the average sensitivity Φ_AUC(ω, θ, μ^⋆) is maximal at the critical boundary, as seen in Fig. 3b (see Methods and Extended Data Fig. 8 for details). Again, the parameters that best fit the empirical observations (highlighted with a blue cross in Fig. 3b) are close to this boundary, suggesting that the experimentally observed shoals could maximize their sensitivity to external perturbations.

Fig. 3: Information propagation in the critical regime.

a, Illustration of the PZ and SZ for sensitivity analysis. b, Heatmap showing the values of the parameter Φ_AUC(ω, θ, μ^⋆). The blue cross denotes the location of the parameters (ω^⋆, θ^⋆). c, Scheme to describe the training of the RNN for different parameters (ω, θ) to classify the event of a perturbation. The training was implemented using the BPTT technique (Methods). d, Scheme to visualize the PZ and SZ for analysis of the propagation of information through the system. e, Heatmap showing the accuracy of the RNN. We find that the empirically fitted parameters (ω^⋆, θ^⋆) (highlighted with a blue cross) are located where the accuracy peaks.

Second, we characterized the propagation of information through the system by classifying the presence of a perturbation based on the activity in a small SZ at varying location (Fig. 3d). This localized subset of cells aims to emulate the local perspective of small groups of fish in the system. We used a generic machine-learning-based classifier to probe the general ability of the system to identify the perturbations to the system. For this, we used the time-dependent stochastic activation patterns in the SZ from the simulated data. We computed the results in the parameter space defined by θ and ω, in particular the performance at the set of parameters that best fit the experimental observations. We used a recurrent neural network (RNN; LSTM, long short-term memory)³⁵ to integrate the local activity information over time (Fig. 3c, Methods and Extended Data Table 1). For each parameter pair (θ, ω), we trained a separate network, providing a binary prediction at every time step (Fig. 3c). This result, shown in Fig. 3e, is qualitatively similar to the sensitivity analysis (Fig. 3b), suggesting that individuals can detect the presence of a perturbation at a given distance optimally only when the system operates close to the critical region. Taken together, the above analysis demonstrates that, in the model, the critical state facilitates precise and robust propagation of information through the system, something that might also be present in the real-life system.

In summary, by combining empirical data with mathematical modelling, we have shown that the spatiotemporal collective dynamics of large shoals of sulphur mollies correspond to a noise-driven excitable system at criticality. Our estimated exponent for the cluster size distribution is consistent with those observed for the closely related self-organized critical forest fire model by Drossel and Schwabl³⁶. However, as noted by Grassberger³⁷, corresponding estimations are difficult due to strong finite size effects. We further refrain from claims on the exponent belonging to a particular universality class. Although this is a fundamental concept in equilibrium statistical physics, the general relevance of universality for non-equilibrium phase transitions is under debate due to reports of non-universal, parameter-dependent scaling exponents³⁸. A corresponding in-depth investigation of the scaling exponents and scaling relationship is beyond the scope of this work. Furthermore, using two different computational classifying methods, we have shown that operating at the critical point maximizes the discrimination ability of (local) environmental cues of different intensities, as well as the communication range between individuals in different locations of the system. In such natural systems, cue intensity scales with danger, as hunting birds often enter the water with large parts of their bodies, leading to high-intensity visual, acoustic and hydrodynamic perturbations, while overflying birds barely provide visual cues²⁴. Thus, information on the cue intensity is highly relevant for the fish in order to coordinate appropriate responses, including repeated diving for multiple minutes¹⁶. In addition, this information can be communicated across wide distances, allowing fish to take action even when not within the direct area of danger. Being at a critical point potentially allows the sulphur molly shoals to be in a constant state of alertness to environmental perturbations and information on the cue intensity that relates to the danger of these perturbations, which can then be passed most effectively through the shoals. This would suggest that there could be adaptive benefits of the critical state in terms of optimal information processing³⁹. This wide range of empirical observations points to (self-organized) criticality as a possible general organizing principle of collective information processing². Nevertheless, there are also important differences between our system and the other biological systems mentioned above. For example, in neuronal systems, the structure of the interaction network between individual elements changes on a much slower timescale than the dynamical behaviour of the network, so the networks may be assumed to be effectively constant. Such timescale separation is assumed essential for self-tuning of these systems to criticality^10,40. For example, in starling flocks, signatures of criticality have been reported based on short-term observations of highly ordered flocks³³, where network rearrangements are negligible^2,41. For the sulphur molly shoals, the interaction networks between individuals are highly dynamic and change on timescales comparable to the observed behaviour. Thus, our results suggest that self-organized critical behaviour could be a robust feature of biological information processing not requiring such timescale separation, while at the same time pose new fundamental questions on the theoretical description and underlying mechanisms of self-organized adaptation towards criticality.

It remains to be studied how the sulphur mollies—and similar systems that show characteristics of criticality—mechanistically tune themselves towards critical points. Ultimately, criticality has to emerge from the adaptation of individual-level behaviour, such as effective social interactions^3,39,42. It has been shown that the density of sulphur molly shoals exhibits substantial variation over the course of a day²², which in turn modulates the effective strength of social interactions^31,43. This suggests local density to be one core variable controlling the self-organization of living systems to criticality²⁸ and thus a variable to quantify over longer periods of time. However, individual behavioural parameters such as individual speed⁴⁴ or attention to conspecifics⁴⁵ have been shown to have strong effects on collective behaviour, which may yield alternative mechanisms for self-organization towards criticality through modulation of individual behaviour⁴⁶. More generally, this relates also to the recently raised broader question on whether—and if so how—natural collectives and bioinspired artificial systems are capable of flexibly controlling their distance to criticality to modulate their information-processing capabilities depending on the environmental context^28,46.

Methods

Collection of field observations

The field observations were performed in Teapa, a municipality in Tabasco in south-eastern Mexico (17° 33′ N, 93° 00′ W). In this area, there are several sulfidic springs that feed into surrounding surface–water streams and pools. The field work and data collection were performed from 6 April to 11 April 2018 in the largest pond (~600 m²) in the Baños del Azufre spring complex (Fig. 1a). A total of 89 videos were collected, each between 120 and 180 s long. This relatively short length of video recordings was chosen to ensure that, during the observation, as well as at least 180 s before the time window, the system had not been subject to a large external perturbation like a bird attack or bird flyover, to obtain the best possible approximation of spontaneous fish activity given the experimental constraints. The videos were recorded in the afternoon (17:00 to 19:00). The frame rate acquisition of all videos was 50 frames s⁻¹. Figure 1b provides a snapshot.

Rectification process

Each of the videos was rectified to reconstruct a top view of the pond. For this purpose, we positioned a 1.55 m × 1.55 m plastic square on the surface of the water at the end of each recording session. We rectified the videos using the four corner positions of the square and the OpenCV Python library⁴⁷. The rectification process is shown in Fig. 1b.

Background subtraction process

We implemented the background subtraction process to each rectified video using the MOG2 background subtractor from the OpenCV library in Python⁴⁸. After the background subtraction process, the obtained videos consisted only of black and white pixels, as seen in Fig. 1b. For this purpose we used a threshold value of 100 and a history value of 400 in the OpenCV function createBackgroundSubtractorMOG2⁴⁸. We cropped the processed videos to eliminate the black edges of the videos created during the rectification process, as well as the parts of the pond close to the shore, thus keeping only the dynamics in the centre of the pond. The size of all the processed empirical videos is 500 × 500 pixels.

Analysis of the surface-activity signal

We quantified the surface-wave activity of the pond using the processed black-and-white videos. We computed the surface-activity signal ${{{\mathcal{A}}}}{(t)}$, which is defined for each time step (or frame) as the number of white pixels at a given time t divided by the total number of pixels in that frame. Thus, the surface-activity signal ${{{\mathcal{A}}}}{(t)}$ can take values between 0 and 1. From each empirical signal we calculated two quantities that served to characterize the dynamics. These quantities are the mean value ${\langle {{{\mathcal{A}}}}\rangle }_{t}$ and the threshold value ${{{{\mathcal{A}}}}}_{{{{\rm{th}}}}}$. They are defined as

$${\langle {{{\mathcal{A}}}}\rangle }_{t}=\frac{1}{T}\mathop{\sum }\limits_{t=0}^{T}{{{\mathcal{A}}}}{(t)},$$

(1)

$${{{{\mathcal{A}}}}}_{{{{\rm{th}}}}}={\langle {{{\mathcal{A}}}}\rangle }_{t}+2\sqrt{{\langle {({{{\mathcal{A}}}}-{\langle {{{\mathcal{A}}}}\rangle }_{t})}^{2}\rangle }_{t}},$$

(2)

where T is the time duration of the signal. We computed a third quantity from each signal, which is the ratio of both previously defined values:

$${{{\mathcal{R}}}}={\frac{{\langle {{{\mathcal{A}}}}\rangle }_{t}}{{{{{\mathcal{A}}}}}_{{{{\rm{th}}}}}}}.$$

(3)

We used this ratio ${{{\mathcal{R}}}}$ to compare the empirical signals of ${{{\mathcal{A}}}}{(t)}$ with the corresponding signals obtained in numerical simulations. The average value over all empirical videos was ${{{{\mathcal{R}}}}}_{{{{\rm{emp}}}}}={0.33\pm 0.15}$. The numerical values of these quantities are presented in Extended Data Fig. 4 for each video. We used the threshold value ${{{{\mathcal{A}}}}}_{{{{\rm{th}}}}}$ to compute the characteristic times τ₁ (inter-spike time) and τ₂ (spike-duration time), shown in Fig. 1c. The corresponding distributions obtained from the empirical videos are presented in Fig. 1d,e.

Fitting of characteristic times distributions and goodness-of-fit

We fitted the empirically obtained distributions for the characteristic times τ₁ and τ₂ using a gamma distribution:

$${P(\tau )}={\frac{1}{{{\varGamma }}(\kappa )\,\,{\theta }^{\kappa }}\,{\tau }^{\kappa -1}{\rm{e}}^{-\tau /{{\varOmega }}}}$$

(4)

where κ > 0 and Ω > 0 are two free parameters of the distribution and Γ(κ) is the gamma function. We can fit the two parameters of equation (4) using the first two moments of the empirical distributions by computing

$${\kappa }={\frac{{\langle \tau \rangle }^{2}}{{\sigma }^{2}},\,{{\varOmega }}={\frac{{\sigma }^{2}}{\langle \tau \rangle }}},$$

(5)

where σ² = 〈(τ − 〈τ〉)²〉. In this way, we obtain the best candidate to fit the empirical data. To assess the goodness of this fit, we followed a procedure introduced in ref. ³⁰. We first generate a set of random data sampled using a gamma distribution with the parameters κ and θ fitted from the empirical data. We then calculate the D-statistics using the KS distance:

$${D}={\mathop{\max }\limits_{\tau }| {F}_{{{{\rm{synth}}}}}(\tau )-{F}_{{{{\rm{theory}}}}}(\tau )| },$$

(6)

where F_synth(τ) in equation (6) is the cumulative distribution function (CDF) of the synthetically generated data, and F_theory(τ) is the analytic expression of the CDF of the gamma distribution in equation (4), which is

$${F}_{{{{\rm{theory}}}}}{(\tau )}={\frac{1}{{{\varGamma }}(\kappa )}\,\gamma (\kappa ,\,\tau /{{\varOmega }})},$$

(7)

where γ(x, y) is the lower incomplete gamma function, defined as

$${\gamma (x,\,y)}={\int\limits_{0}^{y}{t}^{x-1}{\rm{e}}^{-t}{\rm{d}}t}.$$

(8)

We repeat this process 2,500 times and generate the distribution P(D) with all the obtained values. We now calculate the value of the D-statistics using the empirical data by computing

$${D}_{{{{\rm{emp}}}}}={\mathop{\max }\limits_{\tau }| {F}_{{{{\rm{emp}}}}}(\tau )-{F}_{{{{\rm{theory}}}}}(\tau )| },$$

(9)

where F_emp(τ) is the CDF of the empirical data. We compare the numerical value of D_emp with the distribution generated with the synthetic data and compute the p value as the fraction of values of D lower than D_emp. We show the results in Extended Data Fig. 1 for both characteristic times τ₁ and τ₂. The low p values obtained for both characteristic times (p = 0.013 and p = 0.034, respectively) suggest that the error between the empirical measurements and the analytic expression in equation (4) can be associated only to noise³⁰. We can thus conclude that their distributions are consistent with gamma distributions, which have exponentially decaying tails.

Computation of activity clusters

The activity cluster analysis presented in the main text was implemented using the definition given in ref. ²⁹. We quantified the activity clusters (coherent spatiotemporal structures) by stacking the images of each black-and-white video at equal time intervals Δt and then counting the number of connected spatiotemporal white pixels. The cluster volumes are then defined as the size of these spatiotemporal structures. If we collapse the cluster volumes over the temporal axis, we obtain purely spatial structures that we call cluster areas. The distributions of the cluster volumes and cluster areas are shown in Extended Data Fig. 2. We also computed the speed of each cluster to filter small-sized ones, related to moving objects on the surface of the pond. We used the same methods as used in ref. ¹⁶, and we analysed only the clusters with a speed higher than 0.5 m s⁻¹ to be sure that the analysed clusters were originated by fish activity.

Power-law analysis of the cluster distributions

We implemented an analysis on the empirical distributions of the cluster areas and volumes to quantify how far these distributions are statistically consistent with a power-law distribution of the form

$${P(v)\propto {v}^{-{\alpha }_{v}}},$$

(10)

$${P(a)\propto {a}^{-{\alpha }_{a}}},$$

(11)

where v and a stand for the cluster volumes and cluster areas, respectively. We performed the analysis following ref. ³⁰ and using the Python power-law library⁴⁹. There are two important values that need to be calculated from the data: the minimal value ${a}_{\min }$ (and ${v}_{\min }$) and the exponent α_a (and α_v). With these minimal values ${a}_{\min }$ and ${v}_{\min }$, we can calculate the exponents using maximum likelihood estimators³⁰:

$${\alpha }_{a}={1+{n}_{a}{\left[\mathop{\sum }\limits_{i = 1}^{{n}_{a}}\ln \frac{{a}_{i}}{{a}_{\min }}\right]}^{-1}},$$

(12)

$${\alpha }_{v}={1+{n}_{v}{\left[\mathop{\sum }\limits_{i = 1}^{{n}_{v}}\ln \frac{{v}_{i}}{{v}_{\min }}\right]}^{-1}},$$

(13)

where a_i (with i = 1, …, n_a) and v_i (with i = 1, …, n_v) are the observed empirical values such that ${a}_{i} > {a}_{\min }$ and ${v}_{i} > {v}_{\min }$. Following ref. ³⁰, we obtain the best fitting parameters ${a}_{\min }^{\star }$, ${v}_{\min }^{\star }$, ${\alpha }_{a}^{\star }$ and ${\alpha }_{v}^{\star }$ and we compute the corresponding D-statistics for areas and volumes, which we call ${D}_{a}^{\star }$ and ${D}_{v}^{\star }$. To test the goodness of the fit of these parameters, we generate random data sampled from a power-law distribution with the estimated parameters, analogous to what we explained in the previous section. We then obtain the distributions P(D_a) and P(D_v) and compute the corresponding p values as the fraction of the synthetically generated data where ${D}_{a}\le {D}_{a}^{\star }$ and ${D}_{v}\le {D}_{v}^{\star }$, respectively.

Model implementation

The system consists of a square lattice of L × L cells. The temporal dynamics of the cells is stochastic, and it is computed with a discrete variable that we call q(i, j, t), where i and j are integers that represent the location of the cell within the system, and t is the time. Each cell can be in one of three different states (${{{\mathcal{S}}}},\,{{{\mathcal{D}}}},\,{{{\mathcal{U}}}}$), each one associated to one behaviour as explained in the main text. A snapshot of the numerical simulations is shown in Fig. 2b and in Extended Data Fig. 3a. The transition rate that controls the change of cell ij from state ${{{\mathcal{S}}}}$ to state ${{{\mathcal{D}}}}$ is mathematically expressed as

$${R}_{{{{\mathcal{S}}}}\to {{{\mathcal{D}}}}}^{(ij)}{(x)}={R}_{{{{\rm{int}}}}}^{(ij)}{(x)}+{R}_{{{{\rm{spont}}}}}^{(ij)},$$

(14)

where x is the number of neighbours in state ${{{\mathcal{D}}}}$ of the cell ij. The neighbourhood of each cell is defined as its eight nearest neighbours (Moore neighbourhood; Extended Data Fig. 3b,c). For the interaction term in equation (14) we use a sigmoid function with two parameters called θ and μ:

$${R}_{{{{\rm{int}}}}}^{(ij)}{(x)}={\frac{{(x/\theta )}^{\theta \mu }}{1+{(x/\theta )}^{\theta \mu }}}.$$

(15)

Examples of equation (15) are provided in Extended Data Fig. 3d,e. The spontaneous term in equation (14) is given by

$${R}_{{{{\rm{spont}}}}}^{(ij)}={\omega },$$

(16)

with ω a constant. Notice that the probability of observing a spontaneous transition ${{{\mathcal{S}}}}\to {{{\mathcal{D}}}}$ in the complete system increases with increasing system size as L². We are then left with a total of three free parameters in the model: ω, θ and μ. The transitions ${{{\mathcal{D}}}}\to {{{\mathcal{U}}}}$ and ${{{\mathcal{U}}}}\to {{{\mathcal{S}}}}$ were implemented in a deterministic way. This means that a cell that transitioned to state ${{{\mathcal{D}}}}$ would remain in this state (and thus affect its neighbours that are in state ${{{\mathcal{S}}}}$) for a time ${t}_{{{{\mathcal{D}}}}}$. After this time, the cell would change its state to ${{{\mathcal{U}}}}$. Analogously, a cell in state ${{{\mathcal{U}}}}$ remains a time ${t}_{{{{\mathcal{U}}}}}$ in this state before changing back to state ${{{\mathcal{S}}}}$. These transitions can also be implemented in a stochastic fashion using constant rates such that ${R}_{{{{\mathcal{D}}}}}={1}/{t}_{{{{\mathcal{D}}}}}$ and ${R}_{{{{\mathcal{U}}}}}={1}/{t}_{{{{\mathcal{U}}}}}$. Notice that the stochastic implementation of the transitions ${{{\mathcal{D}}}}\to {{{\mathcal{U}}}}$ and ${{{\mathcal{U}}}}\to {{{\mathcal{S}}}}$ requires the use of a total of three states (${{{\mathcal{S}}}}$, ${{{\mathcal{D}}}}$, ${{{\mathcal{U}}}}$) to have a refractory period between two succesive events where a single cell was in the susceptible state ${{{\mathcal{S}}}}$ (ref. ⁵⁰). For our simulations, we used the values of ${t}_{{{{\mathcal{D}}}}}={1}$ s and ${t}_{{{{\mathcal{U}}}}}={3}$ s. These values correspond to the observations published in ref. ²⁴, where experiments were performed in a controlled environment in the laboratory using small groups of sulphur mollies that were captured in the same sulfidic springs in Teapa. In their experiments, the fish were exposed to artificial visual and acoustic stimuli presented separately or combined. They measured—among other observables—the diving duration (called fast-start duration in Fig. 4c of ref. ²⁴), as well as the total dive duration (shown in Fig. 4e of ref. ²⁴). The numerical values of ${t}_{{{{\mathcal{D}}}}}$ and ${t}_{{{{\mathcal{U}}}}}$ used in our simulations were chosen to reproduce the observations done for the bimodal stimulus.

For the numerical results presented in Fig. 2 in the main text, we used the Euler–Maruyama method⁵¹ to compute the time evolution of the model. For all panels in the figure, the time step was Δt = 0.1s and the system size was L × L = 250,000 cells. For Fig. 2c,g, the number of time steps was 1,300 (equal to 130s) and only one realization was required for each plot. For Fig. 2d–f, the number of time steps was 5,000,000 and, again, only one realization was required to acquire the data for the three distributions. Finally, for Fig. 2h,i, the number of time steps was 50,000 (per realization) and 10,000 realizations were computed for each set of parameters (neighbour coupling θ and spontaneous rate ω). The value of each point in Fig. 2h,i is the average correlation function over all realizations. For details on the computation of the results in Fig. 2h,i, see the Average correlation function section.

Fitting of the parameters of the model

We fitted the parameters ω, θ and μ by comparing the empirical data with the numerical simulations via two quantities, the first being the previously defined ratio ${{{\mathcal{R}}}}$ and the second one the average number of active neighbouring cells, which we call ${{{\mathcal{N}}}}$. The ratio ${{{\mathcal{R}}}}$ is a quantity related to the temporal dynamics of the system, and ${{{\mathcal{N}}}}$ is instead related to the spatial properties of the observed patterns in the natural system. We computed ${{{\mathcal{N}}}}$ by randomly selecting time frames from each video and computing the number of neighbouring cells in state ${{{\mathcal{D}}}}$ of randomly selected focal cells, as depicted in Extended Data Fig. 5. From each video we sampled 2,000 randomly selected frames, and we selected 2,500 cells from each frame as focal cells. The average value obtained over all empirical videos is ${{{{\mathcal{N}}}}}_{{{{\rm{emp}}}}}={0.27\pm 0.23}$. To find the best fitting parameters, we define two auxiliary functions, ${\epsilon }_{1}{(\omega ,\,\theta ,\,\mu )}=| {{{{\mathcal{R}}}}}_{{{{\rm{emp}}}}}-{{{{\mathcal{R}}}}}_{{{{\rm{sim}}}}}{(\omega ,\,\theta ,\,\mu )}|$ and ${\epsilon }_{2}{(\omega ,\,\theta ,\,\mu )}=| {{{{\mathcal{N}}}}}_{{{{\rm{emp}}}}}-{{{{\mathcal{N}}}}}_{{{{\rm{sim}}}}}{(\omega ,\,\theta ,\,\mu )}|$, where ${{{{\mathcal{R}}}}}_{{{{\rm{sim}}}}}{(\omega ,\,\theta ,\,\mu )}$ and ${{{{\mathcal{N}}}}}_{{{{\rm{sim}}}}}{(\omega ,\,\theta ,\,\mu )}$ are the resulting values obtained in the numerical simulations for a given set of parameters (ω, θ, μ). For a fixed value of μ, we can plot the two functions ϵ₁ and ϵ₂ in the 2D space defined by ω and θ. The corresponding plots for the case μ = 1 are shown in Extended Data Fig. 3f,g. When we compute the values of ω and θ that minimize the functions ϵ₁ and ϵ₂ (Extended Data Fig. 3f,g, orange lines), we can find the set of parameters ω^⋆ and θ^⋆ that minimize both auxiliary functions simultaneously, namely the crossing of both orange lines, highlighted with a blue cross in Extended Data Fig. 3f,g. We can look for the corresponding parameters ω^⋆ and θ^⋆ for every given value μ. We implemented numerical simulations for different values of μ and compared them via the function ${{{\widehat{\boldsymbol{\epsilon }}}}}{({\omega }^{\star },\,{\theta }^{\star },\,\mu )}={\epsilon }_{1}{({\omega }^{\star },\,{\theta }^{\star },\,\mu )}+{{\epsilon }_{2}({\omega }^{\star },\,{\theta }^{\star },\,\mu )}$. The values of ${{{\widehat{\boldsymbol{\epsilon }}}}}{({\omega }^{\star },\,{\theta }^{\star },\,\mu )}$ are shown in Extended Data Fig. 3h. Notice that the minimal value is reached for a value of μ = μ^⋆ = 1. Thus, the best fitting parameters are ω^⋆ = 0.6 × 10⁻⁵, θ^⋆ = 2.5 and μ^⋆ = 1.

Analysis of the critical transition in the model

To provide further evidence that the transition observed in the model is indeed critical, we analysed the susceptibility of the mode as a function of the system size. For this, we highlight that the phase transition is mainly driven by the neighbour coupling θ, as observed in Fig. 2h, Fig. 3b,e and Extended Data Fig. 3g. Thus, to simplify the analysis, we fixed the spontaneous rate ω and parameter μ to their optimal values (ω^⋆, μ^⋆) and performed a more thorough analysis by varying only the parameter θ. For a given value of this parameter, we computed the average mean square fluctuations of the activity signal ${{{\mathcal{A}}}}{(t)}$—that is, the susceptibility—defined as

$${\chi (\theta )}={{L}^{2}\times \left[\langle {{{{\mathcal{A}}}}}^{2}\rangle -{\langle {{{\mathcal{A}}}}\rangle }^{2}\right]},$$

(17)

where L is the system size (and L × L is the number of cells in the system). We computed the susceptibility χ for six different system sizes: L ∈ [25, 50, 100, 200, 400, 800]. We show the results in Extended Data Fig. 6a. In all cases, and for all system sizes, the susceptibility peaks in an interval between θ = 2 and θ = 3 (approximately). We can easily notice that the numerical value of the susceptibility at the peak increases with increasing system size L. We obtained the value of θ at which the susceptibility χ reaches its maximum value (peak) and called it θ_c. We compared the effect of the system size L on the values of the susceptibility for three different regimes: θ < θ_c, θ = θ_c and θ > θ_c. The results are shown in Extended Data Fig. 6b, where we can see that the numerical value of the susceptibility increases with increasing system size L only for the case θ = θ_c, and remains constant for the other two regimes. In that case, susceptibility χ diverges with an exponent of ~1.7.

To better quantify this result, we computed the width of the peak of the susceptibility χ—called ${{{\mathcal{W}}}}$—defined as

$${{{{\mathcal{W}}}}}^{2}={\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{\chi }_{i}\times {({\theta }_{i}-{\theta }_{\rm{c}})}^{2}},$$

(18)

where N is the sum of susceptibility values ${\mathop{\sum }\nolimits_{i = 1}^{N}{\chi }_{i}}$, θ_c is the value for which the susceptibility reaches its maximum for each system size L, and χ_i and θ_i are the numerical values plotted in Extended Data Fig. 6a for all system sizes. The results are plotted in Extended Data Fig. 6c for all system sizes, where we observe that the width ${{{\mathcal{W}}}}$ decreases with increasing system size L. From these results we can conclude that the transition we observe in the model is indeed of a critical nature, given that the susceptibility peaks at θ_c (a good method to identify the critical regime), and the larger the system size L, the larger and thinner the peak.

Computation of the susceptibility in empirical data

As a complement to the analysis of the critical transition in the model, we computed the susceptibility—as defined in equation (17)—in the empirical videos. For this, we used different window sizes L_W of the original videos and computed the surface-activity signal ${{{\mathcal{A}}}}{(t)}$ in that window. We show the results in Extended Data Fig. 7, where we notice that, in all cases, the susceptibility increases with window size, which strongly suggests that the real-life system operates at criticality. We highlight that the the best fitting power laws for the different acquisition days have an exponent between 1 and 2. As shown in the previous subsection, the exponent obtained in the model (numerical value of ~1.7) lies within the same range. Furthermore, there are three days (180407, 180410 and 180411) where the best fit to the empirical data is indeed very close to the numerical result of the model. There are different potential explanations for this variability observed in the exponent: the different camera set-ups or camera position or the time of the day at which the videos were taken. Furthermore, the distribution of the fish in the region of interest may vary slightly over the course of different recordings, which, together with finite size effects, may lead to variation in the corresponding exponents. A corresponding detailed investigation is beyond the scope of this work.

Average correlation function

To quantify the correlation of the fluctuations of the activity of the system, we computed the average correlation function 〈c(ω, θ, μ)〉, as done in ref. ¹⁵. We first computed the time average value of the variable q(i, j, t) by calculating

$${\langle q(i,\,j)\rangle }_{t}={\frac{1}{T}\mathop{\sum }\limits_{t=0}^{T}q(i,\,j,\,t)},$$

(19)

where T is the observation time and q(i, j, t) = 1 if the cell is in the active state ${{{\mathcal{D}}}}$ and q(i, j, t) = 0 otherwise. We can then compute the correlation of the fluctuations of all cells in the system with its neighbours at a given time t:

$${c(t| \omega ,\,\theta ,\,\mu )}={\frac{\mathop{\sum }\limits_{i,\,j=1}^{L}\,\mathop{\sum}\limits_{l,\,p\in {{{\varOmega }}}_{ij}}\left(q(i,\,j,\,t)-{\langle q(i,\,j)\rangle }_{t}\right)\left(q(l,\,p,\,t)-{\langle q(l,\,p)\rangle }_{t}\right)}{\mathop{\sum }\limits_{i,\,j=1}^{L}{\left(q(i,\,j,\,t)-{\langle q(i,\,j)\rangle }_{t}\right)}^{2}}},$$

(20)

where Ω_ij is the set of neighbours of a given cell ij. The resulting function in equation (20) depends on the values of the parameters ω, θ and μ. To compare the correlation for different parameter values, we computed the time average of equation (20) as

$${\langle c(\omega ,\,\theta ,\,\mu )\rangle }_{t}={\frac{1}{T}\mathop{\sum }\limits_{t=0}^{T}c(t| \omega ,\,\theta ,\,\mu )}.$$

(21)

For the plot in Fig. 2h we computed the average value of ${\langle c(\omega ,\,\theta ,\,{\mu }^{\star })\rangle }_{t}$ over 10,000 realizations, where each realization consisted of 50,000 time steps. Cuts at ω = ω^⋆ and θ = θ^⋆ are also shown in Fig. 2i.

Perturbation analysis

We explored the effect of perturbations on the numerical simulations of the model. For this purpose, we considered five different perturbation intensities by perturbing a different number of cells in the PZ (Fig. 3a). The total area of the PZ—called ${{{{\mathcal{V}}}}}_{\rm{PZ}}$—represents 1.5% of the total area of the system. The main reason is that we aim to study the effect of strong and highly localized perturbations on the system. For the results presented in the main text, we used a system of size L × L = 25 × 25 cells (this is, a localized analysis) and thus the total area of the PZ was ${{{{\mathcal{V}}}}}_{\rm{PZ}}={3\times 3}$ cells. The five different intensities were selected to represent a fraction of ${{{{\mathcal{V}}}}}_{\rm{PZ}}$ such that ${{{\mathcal{I}}}}\in {\{1,\,3,\,5,\,7,\,9\}}$.

Sensitivity analysis

We implemented the ROC analysis to quantify the effect of the perturbations on the system. To obtain a binary classification, we implemented numerical simulations with no perturbation (TN case) and compared them with simulations perturbed with the five different intensities (TP cases). For all cases, we sampled the dynamics of all cells in the sample zone SZ (Fig. 3a) of total area ${{{{\mathcal{V}}}}}_{\rm{SZ}}={3\times 3}$ cells. We computed the activity signal of the cells in the SZ—called ${{{{\mathcal{A}}}}}_{{{{{\rm{SZ}}}}}}{(t)}$—for an observation time T = 2,000, and we computed the time average:

$${\langle {{{{\mathcal{A}}}}}_{{{{\rm{SZ}}}}}\rangle }={\frac{1}{T}\mathop{\sum }\limits_{t=0}^{T}{{{{\mathcal{A}}}}}_{{{{\rm{SZ}}}}}(t)}.$$

(22)

We implemented 5,000 realizations (using the Euler–Maruyama method, a time step of Δt = 0.1 and a system of size L × L = 625 cells) for a given set of parameters (ω, θ, μ^⋆) and obtained the corresponding probability distribution ${P}({{{{\mathcal{A}}}}}_{{{{\rm{SZ}}}}})$. We then calculated the FP versus TP curve, as shown in Extended Data Fig. 8. The AUC of the FP versus TP curves for a given perturbation intensity ${{{\mathcal{I}}}}$ is referred to in the following as ${{{\rm{AUC}}}}{(\omega ,\,\theta ,\,{\mu }^{\star },\,{{{\mathcal{I}}}})}$. To simplify the comparison between parameters, we computed the average response to all the five external stimuli:

$${{{\varPhi }}}_{{{{\rm{AUC}}}}}{(\omega ,\,\theta ,\,{\mu }^{\star })}={\frac{1}{5}\mathop{\sum}\limits_{{{{\mathcal{I}}}}}{{{\rm{AUC}}}}(\omega ,\,\theta ,\,{\mu }^{\star },\,{{{\mathcal{I}}}})}.$$

(23)

We plot the resulting values for the parameter space (ω, θ, μ^⋆) in Fig. 3b. For a plot in the reduced space (ω^⋆, θ, μ^⋆), see Extended Data Fig. 8.

Propagation of information analysis

We studied also the propagation of the information of external stimuli in the system. For this, we used machine-learning algorithms. We generated numerical data for different values of (ω, θ, μ^⋆) at a sampling rate of Δt = 0.1s, for an observation time of T = 40s and a system size of L = 25. We generated 10,000 realizations and for each one, a random perturbation time t_p was selected in the interval t_p ∈ [20s, 40s]. We used perturbation intensities in the interval ${{{\mathcal{I}}}}\in {[1,\,9]}$ and compared them with simulations where no perturbation was implemented. More specifically, a single realization is a sequence of 2D arrays ${{{\bf{X}}}}\in {{\mathbb{R}}}^{(T/{{\Delta }}t)\times L\times L}$, which records the dynamics of the system. For each realization, we computed an auxiliary perturbation temporary series, which is a single vector ${{{\bf{Y}}}}\in {{\mathbb{R}}}^{(T/{{\Delta }}t)}$, whose entries are 0 before the perturbation and 1 for all perturbations where the number of perturbed cells exceeds a threshold N_thresh. Hence, it is a binary classification task. For the perturbation analysis, we discarded the first 20 time units because they correspond to an initial stationary settling period. This results in a time-series of size (200, 25, 25) for a single sequence. From each of the realizations we sub-sample (without replacement) three 3 × 3 sub-patches next to the PZ. These sub-patches aim to emulate the local-agent perspective. To reduce the memory requirements of our simulations, we furthermore downsample the time dimension and only keep every second time step. The final dataset used to train the networks consists of 30,000 sub-patch sequences of shape (100, 3, 3).

LSTM training

From the numerical simulations we obtained a high-dimensional time-series of regressors and their corresponding perturbation labels across time. These arrays were reshaped into a vector format to be processed by the RNN. We first embedded X_t by using a linear layer with 128 hidden units. The embedded input patch, ${\tilde{X}}_{t}\in {{\mathbb{R}}}^{128}$, was then processed by the RNN. We used a common LSTM³⁵ layer, which maintained a hidden state h_t and a cell state c_t. Given an input, these states are updated using a combination of input, forget, update and output gates:

$$\begin{array}{rl}{f}_{t}&=\sigma \left({U}^{\,f}{\tilde{X}}_{t}+{W}^{f}{h}_{t-1}+{b}^{\,f}\right)\\ {i}_{t}&=\sigma \left({U}^{i}{\tilde{X}}_{t}+{W}^{\,i}{h}_{t-1}+{b}^{i}\right)\\ {\tilde{c}}_{t}&=\tanh \left({U}^{c}{\tilde{X}}_{t}+{W}^{\,c}{h}_{t-1}+{b}^{c}\right)\\ {c}_{t}&={f}_{t}\odot {c}_{t-1}+{i}_{t}\odot {\tilde{c}}_{t}\\ {o}_{t}&=\sigma \left({U}^{o}{x}_{t}+{W}^{o}{h}_{t-1}+{b}^{o}\right)\\ {h}_{t}&=\tanh ({c}_{t})\odot {o}_{t}.\end{array}$$

Afterwards, the resulting hidden state h_t is processed by another linear layer to provide the readout logits used to classify the presence of a perturbation. The networks are trained to optimize a simple binary cross-entropy loss using backpropagation through time (BPTT) and the Adam optimizer:

$${\mathop{\min }\limits_{\theta }{{{\mathcal{L}}}}({{{\bf{X}}}},\,{{{\bf{Y}}}})}={-\frac{1}{T}\mathop{\sum }\limits_{t=1}^{T}\mathop{\sum }\limits_{c=1}^{2}{Y}_{t,\,c}\times \log \left[{p}_{\theta }\left({Y}_{t,\,c}| {X}_{1},\,\ldots ,\,{X}_{t}\right)\right]},$$

(24)

where p_θ(⋅) denotes the class probabilities predicted by the LSTM. We rewrite Y as a binary one-hot encoded matrix, were c denotes a specific perturbation class. At each time step the network receives an 18D vector input. The networks were trained on 12 CPU cores each and we used the PyTorch⁵² automatic differentiation library. All results shown were obtained by repeating the same procedures for five independent runs with different random seeds. The technical details and parameters used for the training of the networks are listed in Extended Data Table 1.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this Article.