Abstract
The coupling between superconductors and oscillation cycles of light pulses, i.e., lightwave engineering, is an emerging control concept for superconducting quantum electronics. Although progress has been made towards terahertz-driven superconductivity and supercurrents, the interactions able to drive non-equilibrium pairing are still poorly understood, partially due to the lack of measurements of high-order correlation functions. In particular, the sensing of exotic collective modes that would uniquely characterize light-driven superconducting coherence, in a way analogous to the Meissner effect, is very challenging but much needed. Here we report the discovery of parametrically driven superconductivity by light-induced order-parameter collective oscillations in iron-based superconductors. The time-periodic relative phase dynamics between the coupled electron and hole bands drives the transition to a distinct parametric superconducting state out-of-equalibrium. This light-induced emergent coherence is characterized by a unique phase–amplitude collective mode with Floquet-like sidebands at twice the Higgs frequency. We measure non-perturbative, high-order correlations of this parametrically driven superconductivity by separating the terahertz-frequency multidimensional coherent spectra into pump–probe, Higgs mode and bi-Higgs frequency sideband peaks. We find that the higher-order bi-Higgs sidebands dominate above the critical field, which indicates the breakdown of susceptibility perturbative expansion in this parametric quantum matter.
Similar content being viewed by others
Main
Alternating ‘electromagnetic’ bias, in contrast to d.c. bias, is emerging as a universal control concept to enable dynamical functionalities by terahertz (THz) modulation1,2,3,4,5,6,7,8,9,10. THz-lightwave-accelerated superconducting (SC) and topological currents8,9,11,12,13,14,15,16,17,18 have revealed exotic quantum dynamics, for example, high harmonics9,11,19 and gapless quantum fluid states20, and light-induced Weyl and Dirac nodes1,15. However, high-order correlation characteristics far exceeding the known two-photon light coupling to superconductors are hidden in conventional single-particle spectroscopies and perturbative responses, where a mixture of multiple excitation pathways contribute to the same low-order responses21,22. A compelling solution to sensing light-induced SC coherence far from equilibrium is to be able to identify their correlations and collective modes8,23,24,25,26,27,28. The dominant collective excitations of the equilibrium SC phase range from amplitude oscillations (Higgs mode) to oscillations of interband phase differences (Leggett mode) of the SC order parameter. Although amplitude modes have been observed close to equilibrium when external a.c.9,19 and d.c.18,29,30 fields break inversion symmetry (IS), the order-parameter phase–amplitude coherent oscillations have never been observed in spite of their fascinating opportunity to parametrically drive quantum phases.
Figure 1a illustrates the parametrically driven SC state, which is characterized by distinct phase–amplitude collective modes arising from strong light-induced couplings between the amplitude and phase channels in iron-based superconductors (FeSCs). The ground state of FeSCs is known to have s±, rather than Bardeen–Cooper–Schrieffer (BCS), pairing symmetry, which is determined by strong coupling between the electron (e) and hole (h) bands. The state can be viewed as the relative orientation of correlated Anderson pseudo-spins located at different momentum points k (ref. 9). Up and down pseudo-spins correspond to filled and empty (k, −k) Cooper-pair states, whereas canted spins are the superposition of these up and down pseudo-spins. In FeSCs, the pseudo-spins are anti-parallelly oriented between the e−h bands with order-parameter phase difference of π (red and blue arrows, Fig. 1a (top left)) (the ‘THz-MDCS of Anderson pseudo-spin canting states’ section). The THz-driven dynamics causes time-dependent deviations in this s± relative phase and leads to the precession of the correlated pseudo-spins, which, in turn, parametrically drives pseudo-spin canting (Fig. 1a, top right) from the equilibrium anti-parallel configuration. The latter results from the different dynamics of the SC phase in each band, which leads to different e−h pseudo-spin rotations. Consequently, the strong light-induced coupling between the pseudo-spins (Δρ) in each band and the relative phase between them (Δθ) (Fig. 1a) can lead to phase–amplitude collective oscillations and emergent nonlinear sidebands, absent for either d.c. currents or weak field driving.
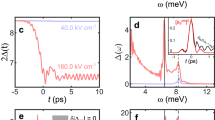
a, Schematic of THz-MDCS via THz-pulse-pair excitations and detections. The schematic of a time-dependent phase-driven Anderson pseudo-spin canting is shown (top right) where the pseudo-spin components are defined by density matrix Δρ (the ‘Gauge-invariant theory and simulations of THz-MDCS signals’ section). The equilibrium anti-parallel pseudo-spin configuration (top left) is non-adiabatically driven by the light-induced time dependence of the order-parameter e–h relative phase Δθ at the Higgs frequency. b, Temporal waveforms of the nearly single-cycle THz pulse pair used in the experiment (red and blue lines). c, Spectra of the used pulses centred at ω0 ≈ 4 meV (vertical dashed arrow); the purple horizontal dashed line indicates the broadband frequency width Δω. d, Temporal dynamics of the measured coherent nonlinear transmission ENL(t, τ)(pink) = EAB(t, τ)(black) − EA(t)(red) − EB(t, τ)(blue) as a function of gate time t at a fixed delay time between the two pulses, namely, −τ = 6.5 ps, under THz driving fields of 229 kV cm−1 at a temperature of 5 K. e, Temporal dynamics of the ENL(t, τ) amplitude decay below (red diamond, 5 K) and above (black cross, 40 K) Tc, as a function of pulse-pair delay time τ under THz driving fields of 333 kV cm−1. The correlated nonlinear signal ENL(t, τ) (red) decays over timescales much longer than the pulse duration.
Terahertz-frequency multidimensional coherent nonlinear spectroscopy (THz-MDCS)12,31,32,33,34,35,36 represents a correlation tomography and control tool to distinguish between different many-body response functions and collective modes. Unlike for THz-MDCS studies of semiconductors12,32,33,37, magnets34 and molecular crystals35, Fig. 1a illustrates three distinct features of our THz-MDCS scheme applied for the first time here on superconductors, to the best of our knowledge. First, our approach is based on measuring the phase of the supercurrent coherent nonlinear emission, in addition to the amplitude, by using phase-resolved coherent measurements with two intense phase-locked THz pulses of similar field strengths. Taking advantage of both real-time and relative phase of the two THz fields, we separate in two-dimensional (2D) frequency-space spectral peaks generated by light-induced correlations and collective mode interactions from the conventional pump–probe (PP), four-wave-mixing (FWM) and high-harmonic-generation signals9,24. This 2D separation of spectral peaks arising from high-order nonlinear processes achieves a ‘super’ resolution of higher-order interactions and collective modes in highly non-perturbative states. This capability is not possible with traditional single-particle or PP spectroscopies9,20,24. Second, as a result of lightwave condensate acceleration by the effective local field inside a thin-film SC induced by THz pulse pairs and electromagnetic propagation effects9, the Cooper pairs (k, –k) of the equilibrium BCS state experience SC pairing with finite centre-of-mass momentum pS(t) (Fig. 1a). Precisely, this phase persists well after the two strong pulses and exhibits (k + pS(t)/2, –k + pS(t)/2) Cooper pairing, due to dynamical symmetry breaking of the centrosymmetric pairing states9. Third, the finite-momentum-pairing quantum state with supercurrent flow that is directly proportional to pS(t) controllable by two-pulse interference can host distinct collective modes that parametrically drive the time-dependent pseudo-spin oscillators. This process triggers the phase–amplitude dynamics illustrated in Fig. 1a, whose nonlinear interactions determine the THz-MDCS spectral profile36.
In this Article, we reveal a parametrically driven SC state by time-periodic light-induced dynamics of the order parameter phase in a Ba(Fe1−xCox)2As2 superconductor. Such an effect parametrically drives time-dependent Anderson pseudo-spin canting and precession from the anti-parallel equilibrium orientation, consistent with our quantum kinetic simulations. Such parametric driving becomes important when the phase dynamics is amplified by a unique phase–amplitude collective mode that develops with increasing THz pulse-pair driving and gives rise to the drastic nonlinear shift from ωHiggs to 2ωHiggs Floquet sideband peaks.
THz-MDCS of FeSCs
We measured Co-doped BaFe2As2 (Ba-122) epitaxial thin film (60 nm) at the optimal doping with Tc ≈ 23 K and lower SC gap of 2Δ1 ≈ 6.8 meV (the ‘Sample preparation and quality’ section). We used THz-MDCS to measure the responses to two phase-locked, nearly single-cycle THz pulses A and B of similar field strength (Fig. 1b), with a central frequency of ω0 ≈ 4 meV (Fig. 1c, black arrow) and broadband frequency width of Δω ≈ 6 meV (Fig. 1c, purple dashed line). Representative time scans of these THz-MDCS experiments driven by laser fields ETHz,A,B = 229 kV cm−1 are shown in Fig. 1d. The measured nonlinear differential emission correlated signal, ENL(t, τ) = EAB(t, τ) − EA(t) − EB(t, τ), was recorded as a function of both gate time t (Fig. 1d) and delay time τ = tB − tA between the two pulses A and B (Fig. 1e). We note three points. First, as demonstrated by ENL(t, τ) (Fig. 1d, pink cross), measured at a fixed delay of −τ = 6.5 ps, the electric field in the time domain allows for simultaneous amplitude-/phase-resolved detection of the coherent nonlinear responses induced by the pulse pair and has negligible contributions from the individual pulses. This is achieved by subtracting the individual responses, EA(t) and EB(t, τ) (Fig. 1b, red and blue solid lines, respectively), from the full signal obtained in response to both phase-locked pulses, namely, EAB(t, τ) (Fig. 1d, black solid line). Second, ENL(t, τ) in Fig. 1e vanishes above Tc, as seen by comparing the 5 K (red diamond) and 40 K (black cross) traces. Third, the THz-MDCS signals persist even when the two pulses do not overlap in time, for example, at −τ = 6.5 ps (Fig. 1d,e). The long-lived correlated signal ENL(t, τ) indicates that the two subgap laser excitations, centred below 2Δ1 (Fig. 1c), have generated robust supercurrent-carrying macroscopic states persisting well after the pulse.
Figure 2 compares the 2D THz temporal profile of the coherent nonlinear signal ENL(t, τ) for relatively weak (Fig. 2a), intermediate (Fig. 2b) and strong (Fig. 2c) driving fields. The ENL(t, τ) dynamics reveals that pronounced coherent temporal oscillations last much longer than the temporal overlap between the two driving pulses (Fig. 1b). One can introduce frequency vectors characterizing the two pulses A and B, namely, ωA = (ω0 ± Δω, 0) and ωB = (ω0 ± Δω, −ω0 ∓ Δω), respectively, which are centred around ω0 ≈ 4 meV (Fig. 1c, black arrow). Following these notations, the observed long-lived coherent responses generate sharp THz-MDCS spectral peaks visible up to ~8 meV below substrate absorption (the ‘Sample preparation and quality’ section). These spectra were obtained by the Fourier transform of ENL(t, τ) with respect to both t (frequency ωt) and τ (frequency ωτ) (Fig. 2d–f). We observe multiple distinguishing and well-defined resonances with unique lineshapes that drastically change with increasing field strength. These ENL(ωt, ωτ) spectra strongly differ from the conventional ones measured, for example, in semiconductors12,32,33, where peaks are observable at multiples of the THz driving pulse frequency ω0 ≈ 4 meV (Fig. 2d–f, magenta dashed line), as expected in the case of a rigid excitation energy bandgap. The observed peaks in FeSCs are much narrower than the excitation pulse width Δω (Fig. 1c, purple dashed line). This result implies that ENL(t, τ) oscillates with the frequencies of SC collective mode excitations that lie within the Δω value of the few-cycle driving pulses. The width of the THz-MDCS spectral peaks is determined by the SC mode damping and not by Δω of the driving pulses.
a–c, Two-dimensional false-colour plot of the measured coherent nonlinear transmission ENL(t, τ) of FeSCs at 5 K induced by THz pump electric fields of 229 kV cm−1(a), 333 kV cm−1(b) and 475 kV cm−1 (c). d–f, Corresponding THz 2D coherent spectra ENL(ωt, ωτ) at 5 K for the three pump electric fields in a (d), b (e) and c (f). Pump frequency ω0 is indicated by the vertical dashed magenta lines. g–i, Normalized ENL(ωt, ωτ) spectra are plotted for the three pump electric fields in a (g), b (h) and c (i) to highlight the pump-field-dependent evolution of the correlation peaks along the 2D frequency vector space. The peaks marked by the dashed lines are located at frequencies associated with the PP signal (black), Higgs mode (green) and bi-Higgs frequency sidebands (red and blue), consistent with the theory shown in Fig. 3.
The normalized ENL(ωt, ωτ) experimental spectra (Fig. 2g–i) visualize the nonlinear couplings of SC collective mode resonances and their field dependences. For the weaker pump field of E0 = 229 kV cm−1 (Fig. 2g), ENL(ωt, ωτ) shows four dominant peaks. Intriguingly, the two strongest peaks, roughly (6, 0) and (6, − 6) meV, are located at higher frequencies, whereas the weaker peaks, slightly below (2, 0) and (2, −2) meV, are located at lower frequencies. This observation is in strong contrast to the expectation from conventional harmonic generation that high-order nonlinear signals should be weaker than lower-order ones. For the intermediate field of E0 = 333 kV cm−1 (Fig. 2h), ENL(ωt, ωτ) shows several peaks close to each other (red and green lines), centred at new frequencies of ~(5, 0) and (5, −5) meV, which exhibit clear non-perturbative behaviour as the dominant high-order THz-MDCS spectral peaks over low-order ones. This observation indicates the breakdown of the susceptibility perturbative expansion that is valid around the SC equilibrium state. The spectral profile changes again with increasing THz driving: four peaks are observable in the THz-MDCS spectrum for the highest studied pump field of E0 = 475 kV cm−1. The two strongest THz-MDCS peaks are roughly located at (2.3, 0) and (2.3, −2.3) meV, whereas two weaker peaks become detectable at (6.2, 0) and (6.2, −6.2) meV (Fig. 2i). These high-field peaks should be distinguished from the low-field ones at similar frequencies (Fig. 2g), as the latter have redshifted with increasing field due to the SC gap reduction. The evolution of THz-MDCS spectral peaks reflects the emergence of different collective modes with increasing driving field, which characterizes the transition to different non-equilibrium SC states.
Light-induced drastic changes in collective modes
We first introduce some basic principles to classify the observed peaks in (ωt, ωτ) space. First, the non-equilibrium SC state driven by the THz pulse pair is characterized by a quenched asymptotic value of the time-evolved SC order parameter, which defines the Higgs frequencies ωH,i = 2Δ∞,i, where i = 1 (i = 2) denotes the h (e) pocket of the FeAs band structure. The above Higgs mode frequencies decrease from their equilibrium values of 2Δ0,i with increasing field, which leads to a redshift in the THz-MDCS spectral features (Fig. 2g–i). Note that we only probe the lower Higgs mode, ωH,1 ≈ 6.8 meV, whereas the higher Higgs frequency, ωH,2 ≈ 19 meV, lies outside the measured spectral range (Fig. 1c). Second, the THz pulses drive the Anderson pseudo-spin oscillators9,36 at different momenta k (the ‘Pseudo-spin canting driven parametrically by phase oscillations’ section). The pseudo-spin dynamics is dominated by frequencies ~ωH,i;A = (ωH,i, 0) and ~ωH,i;B = (ωH,i, − ωH,i), that is, field-dependent Higgs and quasi-particle pair excitations, or ~2ωA,B, that is, quasi-particle excitations driven at the laser frequency.
To identify which nonlinear process generates each peak measured in Fig. 2g–i, we use our quantum kinetic simulations (the ‘Gauge-invariant theory and simulations of THz-MDCS signals’ section) and the above three principles. Lightwave propagation inside an SC thin-film geometry determines the effective driving field \(E(t)={E}_{{{{\rm{THz}}}}}(t)-\frac{{\mu }_{0}c}{2n}J(t)\), which is obtained from Maxwell’s equations38 and differs from the applied field ETHz(t) (n is the refractive index and c is the speed of light). This effective field drives the nonlinear supercurrent J(t), described self-consistently by solving the gauge-invariant SC Bloch equations24,36,38 (the ‘Gauge-invariant theory and simulations of THz-MDCS signals’ section) for a three-pocket SC model with strong e–h pocket interaction U far exceeding the intraband pairing interaction. We directly simulate the ENL(t, τ) temporal dynamics measured in the experiment (Fig. 3a) and then obtain the ENL(ωt, ωτ) spectra (Fig. 3b–e). These simulations are fully consistent with the observed drastic change in the THz-MDCS spectra, where non-perturbative spectral peaks emerging with increasing field (Fig. 2g–i) are indicative of a transition to light-driven SC states with different, emergent collective modes.
a, Example of calculated ENL(t, τ) as a function of gate time t and delay time τ for 250 kV cm−1 pump field. b–e, 2D Fourier transform of ENL(t, τ) for THz pump electric fields of 25 kV cm−1 (b), 250 kV cm−1 (c), 350 kV cm−1 (d) and 700 kV cm−1 (e). The dashed black (blue) lines indicate the PP ωt = ωH,1 − ω0 (bi-Higgs frequency sideband ωt = 2ωH,1 − ω0), whereas IS-breaking signals at Higgs ωt = ωH,1 (bi-Higgs frequency sideband ωt = 2ωH,1 − 2ω0) are marked by the vertical dashed green (red) line; PP peaks at ωt = ω0 are indicated by the vertical dashed magenta line. f, Field-strength dependence of the dominant peak in the spectrum of the interband phase difference ∆θ(ω). g, Field-strength dependence of the bi-Higgs frequency sidebands at 2ωH,1 − ω0 follows the ∆θ(ω) behaviour in f, which identifies the importance of light-induced time-periodic phase dynamics at the ωH,1 frequency in driving a non-equilibrium SC state. Three excitation regimes are marked (main text).
We elaborate the above quantum state transitions by identifying three different excitation regimes. They are marked in Fig. 3f (black dashed lines) and distinguished by the field-strength dependence of the interband phase difference ∆θ(ω) peak: regime (i), the perturbative susceptibility regime; regime (ii), the non-perturbative state with dominant Higgs amplitude mode; regime (iii), the parametrically driven SC state determined by phase–amplitude collective mode. We first examine regime (i), where the Higgs frequency ωH,1 remains close to its equilibrium value, 2Δ1 ≈ 6.8 meV, similar to the ‘rigid’ excitation energy gap in semiconductors. The simulated THz-MDCS spectrum (Fig. 3b) then shows several peaks (Table 1 and Methods) splitting along the ωτ vertical axis, at ωt = ω0 (dashed magenta line) and ωt = ωH,1 (dashed green line). The conventional PP signals are observed at (ω0, −ω0) and (ω0, 0) (Fig. 3b), generated by the familiar third-order processes ωA − ωA + ωB and ωB − ωB + ωA, respectively. FWM signals are also observed at (ω0, ω0) and (ω0, −2ω0), generated by the third-order processes 2ωA − ωB and 2ωB − ωA. However, the perturbative behaviour in this regime is inconsistent with the dominance of higher-order peaks (Fig. 2g) for the stronger fields used in the experiment (to achieve the necessary signal-to-noise ratio).
By increasing the field strength (Fig. 3c–e), the calculated signals along the ωτ vertical axis and at (ω0, −ω0) and (ω0, 0) diminish. Only peaks along (ωt, 0) and (ωt, −ωt) are then predicted by our calculation, consistent with the experiment shown in Fig. 2g–i. For the lower field strength of 250 kV cm−1 (Fig. 3c), our calculated ENL(ωt, ωτ) shows two weak peaks at ωt ≈ 2 meV (black dashed line) and two strong broken IS peaks at ωt = ωH,1 ≈ 6 meV (green dashed line) similar to the experimental THz-MDCS peaks (Fig. 2g). The weak peaks at ωt ≈ 2 meV (black dashed line) arise from the high-order difference-frequency Raman processes (Methods and Table 2, PP), which generate PP signals at ωt = ωH,1 − ω0 (Fig. 2g). The strong peaks at the Higgs frequency ωt = ωH,1 ≈ 6 meV (Fig. 2g,h, green dashed line) dominate for intermediate fields up to ~400 kV cm−1 (Fig. 3f, regime (ii)). However, they vanish if we neglect the electromagnetic propagation effects, as discussed later. The BCS ground state evolves into a finite-momentum-pairing SC state, which is determined by the condensate momentum pS generated by nonlinear processes (Supplementary Fig. 4c and Supplementary Note 4). This condensate momentum persists well after the pulse. Higgs frequency peaks then arise from ninth-order IS-breaking nonlinear processes generated by the coupling between the Higgs mode and lightwave-accelerated supercurrent J(t) (Methods and Table 2, IS Higgs). The superior resolution achieved for sensing the collective modes by using THz-MDCS with 2D coherent excitation is far more than that achieved by using a static IS-breaking scheme using a direct current (Supplementary Fig. 9 and Supplementary Note 7).
For even higher field strengths of 350 kV cm−1 (Fig. 3d) and 700 kV cm−1 (Fig. 3e), the THz-MDCS spectra change above the excitation threshold where the order-parameter phase dynamics becomes substantial (Fig. 3f, regime (iii)). In this regime, new dominant THz-MDCS peaks emerge at ωt = 2ωH,1 − ω0 (Fig. 3d,e, blue dashed line), referred to as bi-Higgs frequency sideband. Satellite peaks are also observed at ωt = 2ωH,1 − 2ω0 (Fig. 3d,e, red dashed line). Figure 3g demonstrates a threshold nonlinear behaviour of these bi-Higgs frequency sideband peak strengths, which coincides with the development of strong phase dynamics (Fig. 3f). These theoretical predictions are fully consistent with our experimental observations (Fig. 2h,i). For the intermediate field (Fig. 3d), the THz-MDCS peaks at ωt = 2ωH,1 − 2ω0 ≈ 4 meV (red dashed line) and ωt = ωH,1 ≈ 6 meV (green dashed line) are close to each other. As a result, they merge into a single broad resonance around (5, 0) and (5, −5) meV, which agrees with the measured broad, overlapping THz-MDCS peaks of ~5 meV (Fig. 2h). The calculated ωt = 2ωH,1 − ω0 peak (Fig. 3d, blue line) is not experimentally visible due to substrate absorption. For the highest studied field strength (Fig. 3e), the calculated THz-MDCS signals are dominated by the bi-Higgs frequency nonlinear sidebands at ωt = 2ωH,1 − ω0 ≈ 6 meV and ωt = 2ωH,1 − 2ω0 ≈ 2 meV (ωH,1 redshifted to ~5 meV with the highest driving field used). Both sidebands peaks now fall into the substrate transparency region and are clearly resolved in Fig. 2i. The emergence of these new THz-MDCS peaks in regime (iii) is a direct manifestation of the phase-driven Anderson pseudo-spin canting (Fig. 1a), as further discussed later.
Figure 4 demonstrates the strong temperature dependence and redshift in the observed peaks as we appoach Tc. The THz-MDCS spectrum ENL(ωt, ωτ) at a temperature of 16 K is shown in Fig. 4a for the intermediate field of E0 = 333 kV cm−1. It is compared in Fig. 2h with the spectrum at T = 5 K for the same excitation. The broken IS signals observed at the Higgs mode frequency ωt = ωH,1 redshift with increasing temperature, from (5.0, 0) and (5.0, −5.0) meV peaks at 5 K to broad peaks slightly below (2.5, −2.5) and (2.5, 0) meV at 16 K (Fig. 4a, green line). This redshift arises from the thermal quench of the SC order parameter 2Δ1 with increasing temperature. However, unlike for the case of THz coherent control of the order parameter (Fig. 2h), a thermal quench does not produce any obvious bi-Higgs frequency THz-MDCS peaks, expected at ~1 meV, which is indicative of the coherent origin of the latter. Figure 4b,c shows the temperature dependence of the measured differential coherent emission ENL(t, τ) and corresponding ENL(ωt, τ) at a fixed pulse separation of −τ = 6.5 ps. By comparing the 5 K (black line) and 22 K (grey) traces (Fig. 4b,c), it is evident that when approaching Tc from below, the coherent nonlinear emissions quickly diminish and redshift. Finally, Fig. 4d,e shows a detailed plot of ENL(ωt, τ) up to 100 K. The integrated spectral weight (Fig. 4d) correlates with the SC transition at Tc (grey dashed line).
a, THz-MDCS spectra ENL(ωt, ωτ) at 16 K for pump electric field of 333 kV cm−1. b, Temporal profiles of two-pulse THz coherent signals ENL(t, τ) at various temperatures from 5 to 22 K for a peak THz pump electric field of Epump = 229 kV cm−1 and −τ = 6.5 ps. Traces are offset for clarity. c, Corresponding Fourier spectra of the coherent dynamics in b. d,e, A 2D false-colour plot of THz coherent signals as a function of temperature and frequency ωt (e) with the integrated spectral weight at various temperatures (d). The dashed grey line indicates the SC transition temperature.
Phase–amplitude mode and parametric driving
Figure 5 offers more insights into the physical mechanism behind the observed transition in the THz-MDCS spectra with increasing field. First, we compare ENL(ωt, ωτ) for a field strength of 250 kV cm−1 between (1) the full calculation that includes electromagnetic propagation and interference effects leading to slowly decaying pS(t) after the pulse (Fig. 5a) and (2) a calculation without electromagnetic propagation effects where pS(t) oscillates during the THz pulse and vanishes afterwards (Fig. 5b). The ωt = ωH,1 peaks vanish in Fig. 5b (green dashed line) and ENL(ωt, ωτ) is dominated by broad PP peaks at ωt = ω0 ≈ 4 meV. This result suggests that the peaks at ωH,1, which dominate the PP peaks in nonlinear regime (ii) (Fig. 2g (experiment) and Fig. 5a (theory)), provide the coherent sensing of non-perturbative Higgs collective modes underpinning the finite-momentum-pairing SC phase (Supplementary Note 7).
a,b, ENL(ωt, ωτ) for the full calculation with lightwave propagation (E0 = 250 kV cm−1) (a) and for a calculation without pulse propagation effects (E0 = 250 kV cm−1) (b). The dashed black (green) lines indicate ωt = ωH,1 − ω0 (ωt = ωH,1). The IS peaks at ωt = ωH,1 vanish without persisting IS breaking. c–e, ENL(ωt, ωτ) for the full calculation with lightwave propagation (E0 = 700 kV cm−1) (c), for a calculation without phase–amplitude coupling (E0 = 400 kV cm−1) (d) and for a calculation without interband interaction, U = 0 (E0 = 100 kV cm−1) (e). To directly compare the different THz-MDCS spectra, the field strengths of the different calculations are chosen such that ωH,1 are comparable, ωH,1 ≈ 5.0 meV. The dashed blue lines indicate ωt = 2ωH,1 − ω0, whereas IS-breaking signals at Higgs ωt = ωH,1 (bi-Higgs ωt = 2ωH,1 − 2ω0) are marked by the vertical dashed green (red) lines. Note that the bi-Higgs frequency sideband peaks are strongly suppressed without phase–amplitude coupling or without interband interaction.
Next, we turn to the transition from Higgs to dominant bi-Higgs signals at ωt = 2ωH,1 − ω0. We associate this transition with the development of a time-dependent pseudo-spin canting from the equilibrium anti-parallel pseudo-spin directions, which is parametrically driven by amplified relative phase dynamics at frequency ωH,1 (the ‘Pseudo-spin canting driven parametrically by phase oscillations’ and ‘Phase–amplitude collective mode and bi-Higgs frequency sidebands’ sections). If the interband Coulomb coupling exceeds the intraband pairing interaction, the Leggett-mode phase oscillations lie well within the quasi-particle continuum (regime (i) for weak THz fields; Fig. 3f), so they are overdamped. Above the critical THz driving (Fig. 3f, regime (iii)), however, the THz-modulated superfluid density of strongly Coulomb-coupled e–h pockets (the ‘Phase–amplitude collective mode and bi-Higgs frequency sidebands’ section and Supplementary Note 4) enhances the nonlinear coupling of the order-parameter phase and amplitude oscillations. This leads to phase oscillations at the same Higgs frequency ωH,1 as the amplitude oscillations, which we refer as to the phase–amplitude collective mode. The latter interacts with quasi-particle excitations at an energy of ~ωH,1, which amplifies the THz-MDCS sideband peaks at frequencies ~2ωH,1 (Fig. 3e). This amplification is at the expense of the Higgs mode peak at ωH,1, which dominates in regime (ii) (Fig. 3f).
To further corroborate the transition from Higgs amplitude to phase–amplitude collective mode, we compare (Fig. 5c,d) the THz-MDCS spectra obtained from the full calculation for 700 kV cm−1 driving with those obtained by turning off the pseudo-spin canting around the s± equilibrium state driven by the ωH,1 time-periodic phase oscillations (Supplementary Figs. 4d and 6 and Supplementary Note 4). Our formulation of the gauge-invariant SC Bloch equations in terms of two coupled pseudo-spin nonlinear oscillators (the ‘Pseudo-spin canting driven parametrically by phase oscillations’ section) shows that non-adiabatic pseudo-spin canting is parametrically driven with the time-dependent strength of \(\sim \vert{{{\varDelta }}}_{1}\vert^{2}\sin (2\Delta \theta )\Delta{\rho }_{1,2}\), where ∆ρ1 and ∆ρ2 are the THz-driven deviations of the x and y Anderson pseudo-spin components from equilibrium, respectively. Such phase-dependent contribution to the nonlinear response is amplified by the strong THz modulation of the superfluid density characterized by light-induced changes in |Δ1|2. Consequently, the threshold nonlinear field dependence of this coupling (Supplementary Fig. 4d) leads to the strong field dependence of the ~2ωH,1 sideband (Fig. 3g). By comparing Fig. 5c,d, we see that the signals at frequencies ωt = 2ωH,1 − ω0 (blue dashed line) and ωt = 2ωH,1 − 2ω0 (red dashed line) are absent when the order parameter phase can be approximated by its equilibrium value. We also compare the full result with a calculation without interband Coulomb interaction between the e and h pockets (Fig. 5e), which again diminishes the bi-Higgs frequency signals.
Conclusion
We demonstrate parametrically driven superconductivity enabled by light-induced phase–amplitude coupling and by time-periodic relative phase dynamics. Higgs coherence tomography of the lightwave-induced high-order correlations and entanglement in parametric quantum matter is of direct interest to quantum information, sensing and superconducting electronics.
Note added after publication: We could have cited ref. 39, as it contributes a potentially helpful item in the existing literature. We thank Dr Matteo Puviani for bringing this to our attention.
Methods
Sample preparation and quality
We measure optimally Co-doped BaFe2As2 epitaxial single-crystal thin films40 (Supplementary Note 8 and Supplementary Figs. 10–12). They are 60 nm thick, grown on 40-nm-thick SrTiO3 buffered (001)-oriented (La;Sr)(Al;Ta)O3 single-crystal substrates. The sample exhibits an SC transition at Tc ≈ 23 K (Supplementary Fig. 11). THz spectra are visible up to ~8 meV below substrate absorption (Supplementary Fig. 12). The base pressure is below 3 × 10−5 Pa and the films were synthesized by pulsed laser deposition with a KrF (248 nm) ultraviolet excimer laser in a vacuum of 3 × 10−4 Pa at 730 °C (growth rate, 2.4 nm s–1). The Co-doped Ba-122 target was prepared by a solid-state reaction with a nominal composition of Ba/Fe/Co/As = 1.00:1.84:0.16:2.20. The chemical composition of the thin film is found to be Ba(Fe0.92,Co0.08)2As1.8, which is close to the stoichiometry of Ba-122 with 8% (atomic percentage) optimal Co doping. The pulsed laser deposition (PLD) targets were made in the same way using the same nominal composition of Ba(Fe0.92,Co0.08)2As2.2.
The epitaxial and crystalline quality of the sample were confirmed by four-circle X-ray diffraction, complex THz conductivity and other extensive chemical, structural and electrical characterizations (Supplementary Figs. 10–12). Equilibrium low-frequency electrodynamics measurements show that the superfluid density ns vanishes above Tc ≈ 23 K and that the lower SC gap is ~6.2–7.0 meV, in agreement with the values quoted in the literature41,42. We measured temperature-dependent electrical resistivity for SC transitions by the four-point method (Supplementary Fig. 11). Onset Tc and Tc at zero resistivity are as high as 23.4 and 22.0 K, respectively, and ΔTc is as narrow as 1.4 K. These are the highest and narrowest values for Ba-122 thin films. In our prior papers, we also checked the zero-field-cooled magnetization Tc and clearly showed a diamagnetic signal by superconducting quantum interference device magnetometer measurements.
THz-MDCS of Anderson pseudo-spin canting states
Following the early work of Anderson43, an SC state can be viewed in terms of an N-spin/pseudo-spin state, with one 1/2 spin at each momentum point interacting with all the rest. The spin texture resulting from this long-range spin interaction, determined by the relative orientation of the different correlated spins located at different momentum points, describes the properties of the SC state. Unlike in one-band SCs with BCS order parameter, the properties of the multiband iron pnictide superconductors studied here are determined by the strong coupling between the e and h bands and the corresponding pseudo-spins. The ground state is known to have s± order parameter symmetry. This means that, in equilibrium, the Anderson pseudo-spins are anti-parallelly oriented between the e and h bands (Fig. 1a). This anti-parallel pseudo-spin orientation between different bands reflects a phase difference of π between the e and h components of the order parameter. Collective excitations of the SC state may be described as magnon-like collective excitations of the Anderson pseudo-spins, whereas quasi-particle excitations correspond to flipping a single spin. THz excitation leads to precession of the correlated pseudo-spins around their equilibrium positions. The new light-driven dynamics proposed here causes time-dependent deviations in the order-parameter relative phase between the e and h bands, which, in turn, parametrically drive Anderson pseudo-spin time-dependent canting from the equilibrium anti-parallel orientation corresponding to the e–h phase difference of π. Such canting from the anti-parallel pseudo-spin orientation between the e and h bands results from the different dynamics of the SC phase in each band, which leads to different e–h pseudo-spin rotations.
Close to equilibrium, time-dependent oscillations of the e–h relative phase that drives pseudo-spin canting results in the Leggett-phase collective modes. These collective modes are additional to the Higgs amplitude modes. However, the Leggett linear response modes are damped in iron pnictides, as their energy lies within the quasi-particle excitation continuum, higher than the frequency of the lower Higgs amplitude mode that coincides with twice the SC gap 2Δ1. Our numerical results presented in the main text show that strong light-induced time-dependent nonlinear coupling of the order-parameter phase and amplitude oscillations leads to phase oscillations at the same Higgs frequency as the amplitude oscillations. We refer to such phase–amplitude simultaneous oscillations at the same frequency of twice the SC energy gap as the phase–amplitude collective mode of the highly driven non-equilibrium state. This phase–amplitude collective mode replaces the Higgs amplitude and Leggett-phase collective modes, which describe the perturbative low-order responses to the THz driving electric field. Since the relative phase of the order-parameter e–h components determines the anti-parallel pseudo-spin configuration that defines the SC equilibrium state of iron pnictides, the development of relative phase oscillations around π at the same frequency as the amplitude Higgs oscillations non-adiabatically drives an ultrafast spin canting from the equilibrium anti-parallel pseudo-spin configuration. Such phase-driven Anderson pseudo-spin canting (Fig. 1a) corresponds to a time-dependent change in the relative pseudo-spin orientation between the e and h bands. This ultrafast canting from the anti-parallel orientation oscillates at the Higgs rather than Leggett frequency above the THz excitation threshold. It is in addition to the collective pseudo-spin precession within each individual band, which describes the hybrid-Higgs light-induced collective mode of iron pnictides introduced in our previous work24. The relative phase oscillations around the equilibrium value of π are long lived when their frequency shifts to the Higgs mode frequency of twice the SC energy gap, which is below the quasi-particle continuum leading to the damping of the Leggett phase mode. Therefore, this frequency shift, induced by the strong light-induced coherent coupling of the order-parameter phase and amplitude oscillations above the threshold field, parametrically drives a non-equilibrium state characterized by time-dependent pseudo-spin canting from the anti-parallel equilibrium configuration. The nonlinear coupling between the pseudo-spin and phase oscillations at the Higgs frequency results in THz-MDCS sidebands at twice the Higgs frequency, which is confirmed by our numerical results in the main text.
To create and characterize the Anderson pseudo-spin canting states, the FeAs SC film is excited with two broadband THz pulses of similar amplitudes, with a centre frequency of ~1.0 THz (4.1 meV) and broadband frequency width of Δω ≈ 1.5 THz (Fig. 1c). The measured nonlinear coherent differential transmission ENL(t, τ) = EAB(t, τ) − EA(t) − EB(t, τ) is plotted as a function of gate time t and the delay time between the two pulses A and B, that is, τ. The time-resolved coherent nonlinear dynamics is then explored by varying the interpulse delay τ between the two THz pulses. Measuring the electric fields in the time domain through electro-optic sampling by a third pulse allows the phase-resolved detection of the sample response as a function of gate time t. The signals arise from third- and higher-order nonlinear PP responses of the SC state, which are separated from the linear response background to obtain an enhanced resolution. Details of our THz setup can be found elsewhere9,20,44,45.
Gauge-invariant theory and simulations of THz-MDCS signals
Details are presented in Supplementary Notes 1 and 2. In thin-film SCs, electromagnetic propagation effects combined with strong SC nonlinearity leads to an effective driving electric field and Cooper-pair centre-of-mass momentum that persist well beyond the duration of the laser pulse. To model both effects in a gauge-invariant way, we use the Boguliobov–de Gennes Hamiltonian46,47
where the fermionic field operators \({\psi }_{\alpha ,\nu }^{{\dagger} }({{{\bf{x}}}})\) create an electron characterized by spin index α and band index ν; ξν(p + eA(x, t)) is the band dispersion, with momentum operator p = −i∇x, vector potential A(x, t) and electron charge −e; μ denotes the chemical potential; and ϕ(x, t) is the scalar potential. The complex SC order parameter component in band ν is given by
The Hartree and Fock energy contributions are
and
respectively, where \({n}_{\sigma ,\nu }({{{\bf{x}}}})=\langle {\psi }_{\sigma ,\nu }^{{\dagger} }({{{\bf{x}}}}){\psi }_{\sigma ,\nu }({{{\bf{x}}}})\rangle\). Here V(x – x′) is the long-ranged Coulomb potential, with Fourier transform Vq = e2/(ε0q2), which pushes the in-gap Nambu–Goldstone mode up to the plasma frequency according to the Anderson–Higgs mechanism43. The Fock energy \({\mu }_{{{{\rm{F}}}}}^{\alpha ,\nu }({{{\bf{x}}}})\) ensures charge conservation. Also, gλ,ν describes the effective interband (λ ≠ ν) and intraband (λ = ν) pairing interactions.
The multiband Hamiltonian (1) is gauge invariant under the general gauge transformation48
when the corresponding vector potential, scalar potential and SC order parameter phases transform as
Here we introduced the field operator in Nambu space, \({{{\varPsi }}}_{\nu }({{{\bf{x}}}})={({\psi }_{\uparrow ,\nu }^{{\dagger} }({{{\bf{x}}}}),{\psi }_{\downarrow ,\nu }({{{\bf{x}}}}))}^{\mathrm{T}}\), and the Pauli spin matrix \({\sigma }_{3}=\left(\begin{array}{ll}1&0\\ 0&-1\end{array}\right)\). However, the density matrix \({\rho }^{(\nu )}({{{\bf{x}}}},{{{\bf{x}}}}^{\prime} )=\langle {\hat{\rho }}^{(\nu )}({{{\bf{x}}}},{{{\bf{x}}}}^{\prime} )\rangle =\langle {{{\varPsi }}}_{\nu }({{{\bf{x}}}}){{{\varPsi }}}_{\nu }^{{\dagger} }({{{\bf{x}}}}^{\prime} )\rangle\) depends on the specific choice of the gauge. To obtain gauge-invariant SC equations of motion, we introduce centre-of-mass and relative coordinates R = (x + x′)/2 and r = x – x′ and define the transformed density matrix38
where \({\rho }^{(\nu )}({{{\bf{r}}}},{{{\bf{R}}}})=\langle {{{\varPsi }}}_{\nu }({{{\bf{R}}}}+\frac{{{{\bf{r}}}}}{2}){{{\varPsi }}}_{\nu }^{{\dagger} }\left.({{{\bf{R}}}}-\frac{{{{\bf{r}}}}}{2})\right)\rangle\). By applying the gauge transformation in equation (5), the density matrix \({\tilde{\rho }}^{(\nu )}({{{\bf{r}}}},{{{\bf{R}}}})\) transforms as38
After applying a Fourier transformation with respect to the relative coordinate r, we perform an additional gauge transformation,
to eliminate phase \({\theta }_{{\nu }_{0}}\) of the SC order parameter for reference band ν0. The equations of motion then depend on the phase difference, \(\delta {\theta }_{\nu }={\theta }_{{\nu }_{0}}-{\theta }_{\nu }\), of the order parameter components between different bands ν ≠ ν0. The latter relative phases also determine the equilibrium symmetry of the multiband SC order parameter (for example, s++ or s±).
Assuming that the multiband SC system is only weakly spatially dependent36,38, we express the gauge-invariant density matrix in terms of Anderson pseudo-spin components at each wavevector k:
Here σn, n = 1,…3, are the Pauli spin matrices, σ0 is the unit matrix and \({\tilde{\rho }}_{n}^{(\nu )}({{{\bf{k}}}})\) are the pseudo-spin components of band ν. We then straightforwardly derive gauge-invariant SC Bloch equations of pseudo-spins, thus generalizing the data from another work38 to the multiband case:
where k± = k ± pS/2. The above equations were solved numerically coupled to Maxwell’s equations to compare with the experiment. Three different sources drive light-induced pseudo-spin motion in the above equations: condensate centre-of-mass momentum pS, effective chemical potential μeff and order-parameter phase difference between different bands ν, namely, \(\delta {\theta }_{\nu }={\theta }_{{\nu }_{0}}-{\theta }_{\nu }\). The coupling of the laser field leads to the time-dependent band energy
This time dependence comes from the light-induced condensate momentum pS(t), the effective chemical potential μeff and the Fock energy
The spin-↑ and spin-↓ electron populations determine the phase-space filling contributions:
Compared with the conventional pseudo-spin models used in the literature before, the gauge-invariant SC Bloch equations (equation (11)) include quantum transport terms proportional to the laser electric field, such as \(e\,{{{\bf{E}}}}\cdot {\nabla }_{{{{\bf{k}}}}}{\tilde{\rho }}_{3}^{(\nu )}({{{\bf{k}}}})\), which also lead to ±pS(t)/2 k-space displacements of the coherences and populations in the finite-momentum-pairing SC state. Dynamically induced IS breaking leads to the coupling between \({\tilde{\rho }}_{0}({{{\bf{k}}}})\) and \({\tilde{\rho }}_{3}({{{\bf{k}}}})\) described by equation (11). As already discussed in other work9,19,20,36,38, by also including the lightwave electromagnetic propagation effects inside the SC system, described by Maxwell’s equations, the above IS breaking persists after the driving pulse.
We obtain the experimentally measured signals by calculating the gauge-invariant supercurrent38
with pseudo-spin component \({\tilde{\rho }}_{0}^{(\lambda )}({{{\bf{k}}}})\). The nonlinear differential transmission measured in the experiment is obtained in terms of J(t) by calculating the transmitted electric field after solving Maxwell’s equations. For a superconducting thin-film geometry, we obtain the effective driving field38
where ETHz(t) is the applied THz electric field, c is the speed of light and n is the refractive index of the SC system. THz lightwave propagation inside the SC thin film is included in our calculation by self-consistently solving equation (16) and the gauge-invariant SC Bloch equations (equation (11))38. Using the above results, we calculated the nonlinear differential transmission-correlated signal measured in the THz-MDCS experiment, which is given by
for the collinear two-pulse geometry used in the experiment (Fig. 1a). EAB(t, τ) is the transmitted electric field induced by both pulses A and B, which depends on both gate time t and delay time between the two pulses, τ. EA(t) and EB(t, τ) are the transmitted electric fields resulting from separate driving by pulse A and pulse B. The THz-MDCS spectra are obtained by the Fourier transform of ENL(t, τ) with respect to both t (frequency ωt) and τ (frequency ωτ). To analyse the spectra, we introduce ‘time vectors’ t′ = (t, τ) and ‘frequency vectors’ (ωt, ωτ), such that the electric fields used in the calculations can be written as EA(t)sin(ωAt′) and EB(t)sin(ωBt′). In these calculations, we assume Gaussian envelope functions EA,B(t′). The corresponding frequency vectors of the two pulses A and B are ωA = (ω0, 0) and ωB = (ω0, −ω0), where ω0 is the central frequency of the pulses.
We solve the gauge-invariant optical Bloch equations (equation (11)) for a three-pocket model with an h pocket centred at the Γ-point and the two e pockets located at (π, 0) and (0, π). We include the inter-e–h pocket interactions (ge,h = gh,e) as well as intrapocket interactions (Vλ = gλ,λ) and neglect the inter-e–e pocket interactions for simplicity. We use an interband-to-intraband interaction ratio of U = ge,h/Vλ = 3 to model the dominance of interband coupling between the e–h pockets over the intraband interaction in FeSCs. The pockets are described by using the square lattice nearest-neighbour tight-binding dispersion ξν(k) = –2[Jν,xcos(kx) + Jν,ycos(ky)] + µν with hopping parameter Jν,i and band offset μν. We choose a circular h pocket with J1,x = J1,y = 25.0 meV and μ1 = −15.0 meV. We introduce the known particle–hole asymmetry between the e and h pockets in our system49,50,51 by considering elliptical e pockets with J2,x = J3,y = −25.0 meV, J2,y = J3,x = −80.0 meV and μ2 = μ3 = 15.0 meV. Such asymmetry strongly suppresses the higher Higgs mode in the spectra of ENL in our calculation, as discussed elsewhere24. We assume s± pairing symmetry with equilibrium SC order parameters Δ1 = 3.4 meV for the h pockets and Δ2 = Δ3 = 9.7 meV for the e pockets. The multiband SC system is excited with two equal broadband pulses with centre frequency ω0 = 1 THz.
Pseudo-spin canting driven parametrically by phase oscillations
To identify the physical origin of the THz-MDCS peaks, we derive nonlinear oscillator equations of motion from the full gauge-invariant equations of motion (equation (11)). Details are discussed in Supplementary Note 3. First, we express the density matrix \({\tilde{\rho }}^{(\nu )}({{{\bf{k}}}})\) describing the non-equilibrium SC state as
where \({\tilde{\rho }}^{(\nu ),{{{\rm{0}}}}}({{{\bf{k}}}})\) is the density matrix of the equilibrium (stationary) state and \({{\Delta }}{\tilde{\rho }}^{(\nu )}({{{\bf{k}}}})\) is the non-equilibrium change induced by the strong driving fields. We consider s± symmetry in the SC ground state, as in the studied iron pnictide system. Then, \(\delta {\theta }_{\nu }^{0}=0,\,\uppi\) defines the equilibrium pseudo-spin orientations in the different bands, whereas \({\tilde{\rho }}_{2}^{(\nu ),{{{\rm{0}}}}}({{{\bf{k}}}})=0\) and \({\tilde{\rho }}_{1}^{(\nu ),{{{\rm{0}}}}}({{{\bf{k}}}})\ne 0\), that is, the pseudo-spins point along the x axis and are anti-parallel between the e and h bands. By taking the second time derivative of equation (11), we obtain the deviations of the x and y pseudo-spin components from equilibrium, namely, \({{\Delta }}{\tilde{\rho }}_{1}^{(\nu )}({{{\bf{k}}}})\) and \({{\Delta }}{\tilde{\rho }}_{2}^{(\nu )}({{{\bf{k}}}})\), respectively, in terms of equations of motion for two nonlinearly coupled oscillators:
The above coupled oscillator equations of motion describe light-induced pseudo-spin canting parametrically driven by long-lived time-dependent phase oscillations \({{\Delta }}{\theta }_{\nu }=\delta {\theta }_{\nu }-\delta {\theta }_{\nu }^{0}\). Also, \(\delta {{{\varDelta }}}_{\nu }^{\prime}={{{\varDelta }}}_{\nu }^{\prime}-{{{\varDelta }}}_{\nu ,0}^{\prime}\) and \(\delta {{{\varDelta }}}_{\nu }^{^{\prime\prime} }={{{\varDelta }}}_{\nu }^{^{\prime\prime} }\) describe the light-induced order-parameter collective dynamics, where we introduced the real and imaginary parts of the complex-valued order parameters
The first terms on the right-hand side of equation (19), \({S}_{\nu }^{(1,2)}({{{\bf{k}}}})\), describe pseudo-spin driving by sum- and difference-frequency Raman and quantum transport processes, previously discussed in another work36, modified here by Δθν ≠ 0 (Supplementary Note 3). The second term on the right-hand side of equation (19), proportional to the light-induced order parameter deviations from equilibrium \(\delta {{{\varDelta }}}_{\nu }^{\prime}\) and \(\delta {{{\varDelta }}}_{\nu }^{^{\prime\prime} }\), describes the collective modes arising from the non-perturbative coupling of the different k pseudo-spins.
The main new effect here comes from the parametric driving of the nonlinear oscillator equations of motion (equation (19)) by the time-dependent order-parameter relative phase Δθν(t). This parametric driving results in non-adiabatic canting of the pseudo-spins from their equilibrium directions defined by \(\delta {\theta }_{\nu }^{0}=0,\uppi\). It originates from the dependence of the left-hand side of equation (19) on Δθν(t), which is enhanced by the phase–amplitude collective mode of the driven non-equilibrium SC state, discussed in the next section. By expanding the nonlinear-coupled-oscillator equations of motion to the lowest order in driving Δθν(t) and pS(t), we show that pseudo-spin canting from the equilibrium direction, \({{\Delta }}{\tilde{\rho }}_{2}^{(\nu )}({{{\bf{k}}}})\ne 0\), is described by the time-dependent coupling to
where ∂tEν(k) ≈ e (E(t) ⋅ ∇k)(pS ⋅ ∇k) ξ(k) is approximated by expanding the band dispersions in powers of the centre-of-mass momentum pS. Equation (21) drives light-induced pseudo-spin canting determined by the competition between condensate momentum and order-parameter relative phase dynamics oscillating at ~ωH,1. In particular, ∂tEν(k) drives pseudo-spin canting via difference-frequency Raman processes ωA,B − ωA,B ≈ 0 and sum-frequency Raman processes ωA,B + ωA,B ≈ 2ω0 > ωH,1. On the other hand, the time dependence of the interband phase difference is dominated by strong oscillations close to the Higgs frequency ωH,1, rather than the Leggett mode frequency well within the quasi-particle continuum, when a phase–amplitude collective mode develops above the critical field (Supplementary Fig. 1).
When the quasi-particle excitations are resonantly driven by the pulse E2 spectrum, as is the case for the broad pulses used here, the \(\Delta{\tilde{\rho }}_{1}^{(\nu )}({{{\bf{k}}}})\) spectra are dominated by a momentum-dependent peak centred at the quasi-particle excitation energy,
determined by the quenched order-parameter asymptotic value |Δ1,∞|. The dominant contribution of the pseudo-spin oscillations that determine the time dependence of \({{\Delta }}{\tilde{\rho }}_{1}^{(\nu )}({{{\bf{k}}}})\) comes from quasi-particle excitations close to the excitation energy minimum, which is located close to the Higgs mode energy ωH,1 (Supplementary Fig. 2). As a result, \({{\Delta }}{\tilde{\rho }}_{1}^{(\nu )}({{{\bf{k}}}})\) mainly oscillates close to ωH,1. We thus obtain, through the nonlinear coupling (equation (21)), THz-MDCS sidebands centred at the sum of the frequencies of Δθν(t) oscillations (phase–amplitude collective mode frequency close to ωH,1) and \({{\Delta }}{{{{\rm{\tilde{\rho} }}}}}_{1}^{(\nu )}\) oscillations (quasi-particle excitations close to ωH,1). Above critical driving, this nonlinear coupling is amplified by the light-induced quench of the superfluid density (Supplementary Fig. 4d), as discussed in more detail in Supplementary Notes 3 and 4.
Phase–amplitude collective mode and bi-Higgs frequency sidebands
To clarify the role of the phase–amplitude collective mode in enhancing the parametric pseudo-spin driving, we have studied the field dependence of the order-parameter amplitude spectrum |Δ1(ω)| and the spectrum of the relative phase Δθ(ω) for strong Coulomb interband coupling as in FeSCs studied here (Supplementary Fig. 4a,b). At low fields, |Δ1(ω)| is dominated by a peak at ~ωH,1, whereas Δθ(ω) shows a peak located within the quasi-particle continuum, corresponding to the Leggett mode. This low-field result reproduces previous collective mode results obtained by using susceptibility expansions. With an increasing driving field, nonlinear coupling between the phase and amplitude moves the relative phase mode towards ωH,1 by creating phase–amplitude collective modes. The emergence of a strong Δθ(ω) peak at the Higgs frequency ωH,1 results from a light-induced phase–amplitude collective mode at ωH,1. This collective mode displays strong phase oscillations at ωH,1, which allows the resonant parametric driving of the coupled nonlinear harmonic oscillators (equation (19)). The resulting time-dependent pseudo-spin canting leads to the sideband signals at twice the Higgs energy ωH,1 (Supplementary Fig. 4e).
To clarify the transition from the Higgs collective mode to coupled phase–amplitude mode with energy ωH,1, we compare the field dependence of the persisting superfluid momentum pS (Supplementary Fig. 4c), which breaks the IS and characterizes the strength of the Higgs mode signals at ωt = ωH,1, and the maximum of the |Δ1|2sin2Δθ spectrum (Supplementary Fig. 4d), which drives pseudo-spin canting in response to the time-dependent changes in the relative phase. Here pS arises from the coupling between SC nonlinearity and electromagnetic propagation effects, which determines the effective driving field (equation (16)) dependent on supercurrent J(t). At low driving fields, the increase in pS is proportional to \({E}_{0}^{3}\), since in this regime, it is generated to the lowest order by third-order nonlinear processes when lightwave propagation effects are included38. This initial excitation regime is, however, followed by another excitation regime, where in a two-band SC, the quench of the SC gap is only slightly modified as the driving field increases (Supplementary Fig. 4a). This behaviour is unlike the one-band case19,38 and results from the strong interband coupling between the e and h pockets leading to the formation of a hybrid-Higgs collective mode24. In this non-perturbative excitation regime, the contribution of Higgs collective effects to the nonlinear response dominates over quasi-particle excitations, which results in the different nonlinear increases in pS compared with the initial regime (Supplementary Fig. 4c). Above 600 kV cm−1 driving, a further increase in the driving field leads to a complete quench of the SC gap (results are only shown up to an order parameter quench of 25%; Supplementary Fig. 4), which results in a stronger nonlinear increase in pS compared with the one in the initial excitation regime (Supplementary Fig. 4c). This behaviour is in agreement with the results in one-band superconductors discussed elsewhere19,38. Compared with the increasing superfluid momentum pS, the maximum of the |Δ1|2sin2Δθ spectrum (Supplementary Fig. 4d) remains near zero in the perturbative excitation regime. In this susceptibility regime, parametric time-periodic driving of pseudo-spin canting by the phase dynamics is negligible, and we recover previously obtained results without any bi-Higgs frequency sidebands. However, above the critical laser field, Supplementary Fig. 4d shows a (two-step) nonlinear increase in |Δ1|2sin2Δθ, up to 400 kV cm−1 excitation. In this regime, the coupled phase–amplitude mode emerges when the relative phase mode gets close to ωH,1 (Supplementary Fig. 4b). A further increase in E0 leads to a strong increase in the maximum of the |Δ1|2sin2Δθ spectrum, which coincides with the emergence of the non-perturbative bi-Higgs frequency sidebands in the THz-MDCS spectra (Supplementary Fig. 4e). In this high-excitation nonlinear regime, the SC order parameter is quenched, which leads to a stronger increase in the relative phase oscillation amplitude, enhanced by 1/|Δ1|. Due to the strong nonlinear increase above the driving field threshold (Supplementary Fig. 4d), the pseudo-spin canting driven by |Δ1|2sin2Δθ dominates over that due to the increase in pS (Supplementary Fig. 4c). This is in contrast to the behaviour at lower fields, where pS increases whereas |Δ1|2sin2Δθ remains small. As a result, the THz-MDCS signals generated by the phase–amplitude mode at ωt = 2ωH,1 − ω0 and ωt = 2ωH,1 − 2ω0 dominate over the nonlinear signals at ωt = ωH,1 in the Higgs collective mode.
Nonlinear processes contributing to the THz-MDCS spectra
In this section, we summarize all the nonlinear processes that contribute to the THz-MDCS spectra (Figs. 2 and 3 and Supplementary Notes 5–7). First, we list the conventional PP and FWM signals already known from THz-MDCS spectroscopy experiments on semiconductors. Such peaks significantly contribute to the THz-MDCS spectra here only in the perturbative excitation regime (Fig. 3b) and result from the nonlinear processes summarized in Table 1.
With increasing field strength, new high-order correlated wave-mixing signals emerge, which dominate over the above conventional PP and FWM signals. In particular, lightwave propagation inside the SC system leads to dynamical IS breaking persisting after the pulses. As a result, new wave-mixing signals (IS wave mixing) emerge at ωt = ωH,1, which are generated by nonlinear processes involving amplitude Higgs mode excitation. Bi-Higgs frequency and IS-breaking bi-Higgs frequency (IS bi-Higgs) sideband peaks emerge with increasing field strength and exceed the Higgs signals at elevated E0. In addition, difference-frequency Raman process assisted by quasi-particle excitations leads to high-order correlated PP signals. All the high-order correlated wave-mixing spectral peaks and corresponding nonlinear processes are summarized in Table 2.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Code availability
All computer codes are available from the corresponding author upon reasonable request.
Change history
07 June 2024
A Correction to this paper has been published: https://doi.org/10.1038/s41567-024-02576-z
References
Vaswani, C. et al. Light-driven Raman coherence as a nonthermal route to ultrafast topology switching in a Dirac semimetal. Phys. Rev. X 10, 021013 (2020).
Fausti, D. et al. Light-induced superconductivity in a stripe-ordered cuprate. Science 331, 189–191 (2011).
Kemper, A. F., Sentef, M. A., Moritz, B., Freericks, J. K. & Devereaux, T. P. Direct observation of Higgs mode oscillations in the pump-probe photoemission spectra of electron-phonon mediated superconductors. Phys. Rev. B 92, 224517 (2015).
Knap, M., Babadi, M., Refael, G., Martin, I. & Demler, E. Dynamical Cooper pairing in nonequilibrium electron-phonon systems. Phys. Rev. B 94, 214504 (2016).
Sentef, M. A., Kemper, A. F., Georges, A. & Kollath, C. Theory of light-enhanced phonon-mediated superconductivity. Phys. Rev. B 93, 144506 (2015).
Mitrano, M. et al. Possible light-induced superconductivity in K3C60 at high temperature. Nature 530, 461–464 (2016).
Buzzi, M. et al. Higgs-mediated optical amplification in a nonequilibrium superconductor. Phys. Rev. X 11, 011055 (2021).
Matsunaga, R. et al. Light-induced collective pseudospin precession resonating with Higgs mode in a superconductor. Science 345, 1145–1149 (2014).
Yang, X. et al. Lightwave-driven gapless superconductivity and forbidden quantum beats by terahertz symmetry breaking. Nat. Photon. 13, 707–713 (2019).
von Hoegen, A. et al. Amplification of Superconducting Fluctuations in Driven YBa2Cu3O6+x. Phys. Rev. X 12, 031008 (2022).
Linder, J. & Robinson, J. W. Superconducting spintronics. Nat. Phys. 11, 307–315 (2015).
Maag, T. et al. Coherent cyclotron motion beyond Kohn’s theorem. Nat. Phys. 12, 119–123 (2016).
Reimann, J. et al. Subcycle observation of lightwave-driven Dirac currents in a topological surface band. Nature 562, 396–400 (2018).
Lingos, P. C., Kapetanakis, M. D., Wang, J. & Perakis, I. E. Light-wave control of correlated materials using quantum magnetism during time-periodic modulation of coherent transport. Commun. Phys. 4, 60 (2021).
Luo, L. et al. A light-induced phononic symmetry switch and giant dissipationless topological photocurrent in ZrTe5. Nat. Mater. 20, 329–334 (2021).
Rajasekaran, S. et al. Parametric amplification of a superconducting plasma wave. Nat. Phys. 12, 1012–1016 (2016).
Dienst, A. et al. Bi-directional ultrafast electric-field gating of interlayer charge transport in a cuprate superconductor. Nat. Photon. 5, 485–488 (2011).
Nakamura, S. et al. Infrared activation of the Higgs mode by supercurrent injection in superconducting NbN. Phys. Rev. Lett. 122, 257001 (2019).
Vaswani, C. et al. Terahertz second-harmonic generation from lightwave acceleration of symmetry-breaking nonlinear supercurrents. Phys. Rev. Lett. 124, 207003 (2020).
Yang, X. et al. Terahertz-light quantum tuning of a metastable emergent phase hidden by superconductivity. Nat. Mater. 17, 586 (2018).
Cea, T., Castellani, C. & Benfatto, L. Nonlinear optical effects and third-harmonic generation in superconductors: Cooper pairs versus Higgs mode contribution. Phys. Rev. B 93, 180507 (2016).
Murotani, Y. & Shimano, R. Nonlinear optical response of collective modes in multiband superconductors assisted by nonmagnetic impurities. Phys. Rev. B 99, 224510 (2019).
Krull, H., Bittner, N., Uhrig, G., Manske, D. & Schnyder, A. Coupling of Higgs and Leggett modes in non-equilibrium superconductors. Nat. Commun. 7, 11921 (2016).
Vaswani, C. et al. Light quantum control of persisting Higgs modes in iron-based superconductors. Nat. Commun. 12, 258 (2021).
Giorgianni, F. et al. Leggett mode controlled by light pulses. Nat. Phys. 15, 341–346 (2019).
Udina, M., Cea, T. & Benfatto, L. Theory of coherent-oscillations generation in terahertz pump-probe spectroscopy: from phonons to electronic collective modes. Phys. Rev. B 100, 165131 (2019).
Chu, H. et al. Phase-resolved Higgs response in superconducting cuprates. Nat. Commun. 11, 1793 (2020).
Schwarz, L., Fauseweh, B. & Tsuji, Nea Classification and characterization of nonequilibrium Higgs modes in unconventional superconductors. Nat. Commun. 11, 287 (2020).
Moor, A., Volkov, A. F. & Efetov, K. B. Amplitude Higgs mode and admittance in superconductors with a moving condensate. Phys. Rev. Lett. 118, 047001 (2017).
Puviani, M., Schwarz, L., Zhang, X.-X., Kaiser, S. & Manske, D. Current-assisted Raman activation of the Higgs mode in superconductors. Phys. Rev. B 101, 220507 (2020).
Cundiff, S. T. & Mukamel, S. Optical multidimensional coherent spectroscopy. Phys. Today 66, 44–49 (2013).
Kuehn, W., Reimann, K., Woerner, M., Elsaesser, T. & Hey, R. Two-dimensional terahertz correlation spectra of electronic excitations in semiconductor quantum wells. J. Phys. Chem. B 115, 5448–5455 (2011).
Junginger, F. et al. Nonperturbative interband response of a bulk InSb semiconductor driven off resonantly by terahertz electromagnetic few-cycle pulses. Phys. Rev. Lett. 109, 147403 (2012).
Lu, J. et al. Coherent two-dimensional terahertz magnetic resonance spectroscopy of collective spin waves. Phys. Rev. Lett. 118, 207204 (2017).
Johnson, C. L., Knighton, B. E. & Johnson, J. A. Distinguishing nonlinear terahertz excitation pathways with two-dimensional spectroscopy. Phys. Rev. Lett. 122, 073901 (2019).
Mootz, M., Luo, L., Wang, J. & Perakis, lE. Visualization and quantum control of light-accelerated condensates by terahertz multi-dimensional coherent spectroscopy. Commun. Phys. 5, 47 (2022).
Mahmood, F., Chaudhuri, D., Gopalakrishnan, S., Nandkishore, R. & Armitage, N. P. Observation of a marginal Fermi glass. Nat. Phys. 17, 627–631 (2021).
Mootz, M., Wang, J. & Perakis, I. E. Lightwave terahertz quantum manipulation of nonequilibrium superconductor phases and their collective modes. Phys. Rev. B 102, 054517 (2020).
Puviani, M. & Manskea, D. Quench–drive spectroscopy of cuprates. Faraday Discuss. 237, 125–147 (2022).
Lee, S. et al. Template engineering of Co-doped BaFe2As2 single-crystal thin films. Nat. Mater. 9, 397–402 (2010).
Tu, J. J. et al. Optical properties of the iron arsenic superconductor BaFe1.85Cco0.15As2. Phys. Rev. B 82, 174509 (2010).
Charnukha, A. Optical conductivity of iron-based superconductors. J. Phys.: Condens. Matter 26, 253203 (2014).
Anderson, P. W. Random-phase approximation in the theory of superconductivity. Phys. Rev. 112, 1900–1916 (1958).
Xu, Y. Ultrafast nonthermal terahertz electrodynamics and possible quantum energy transfer in the Nb3Sn superconductor. Phys. Rev. B 99, 094504 (2019).
Charnukha, A. Light control of surface-bulk coupling by terahertz vibrational coherence in a topological insulator. npj Quantum Mater. 5, 13 (2020).
Stephen, M. J. Transport equations for superconductors. Phys. Rev. 139, A197–A205 (1965).
Yang, F. & Wu, M. W. Gauge-invariant microscopic kinetic theory of superconductivity: application to the optical response of Nambu-Goldstone and Higgs modes. Phys. Rev. B 100, 104513 (2019).
Nambu, Y. Quasi-particles and gauge invariance in the theory of superconductivity. Phys. Rev. 117, 648–663 (1960).
Liu, C. et al. Evidence for a Lifshitz transition in electron-doped iron arsenic superconductors at the onset of superconductivity. Nat. Phys. 6, 419–423 (2010).
Fernandes, R. M. & Schmalian, J. Competing order and nature of the pairing state in the iron pnictides. Phys. Rev. B 82, 014521 (2010).
Yang, X. et al. Nonequilibrium pair breaking in Ba(Fe1−xCox)2As2 superconductors: evidence for formation of a photoinduced excitonic state. Phys. Rev. Lett. 121, 267001 (2018).
Acknowledgements
THz spectroscopy work was designed and supported by National Science Foundation 1905981 (M.M. and J.W.). Data processing and analysis (L.L.) was supported by the Ames National Laboratory, the US Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES), Materials Science and Engineering Division, under contract no. DEAC0207CH11358. THz instrument (J.W.) was supported by the W.M. Keck Foundation (initial design and commission) and by the US DOE, Office of Science, National Quantum Information Science Research Centers, Superconducting Quantum Materials and Systems Center (SQMS), under contract no. DE-AC02-07CH11359 (for improved cryogenic operation and for benchmarking of coherent spectroscopy). The work at University of Wisconsin-Madison (J.H.K. and C.B.E) was supported by the US DOE, Office of Science, Basic Energy Sciences (BES), the Materials Sciences and Engineering (MSE) Division, under award no. DE-FG02-06ER46327 (synthesis of pnictide thin films and characterizations of epitaxial thin films). Work by K.E. and J.W.L. was funded by the Gordon and Betty Moore Foundation’s EPiQS Initiative, Grant GBMF9065. Modelling work at the University of Alabama, Birmingham (I.E.P.), was supported by the US DOE under contract no. DE-SC0019137 and was made possible in part by a grant for high-performance computing resources and technical support from the Alabama Supercomputer Authority.
Author information
Authors and Affiliations
Contributions
J.W., M.M. and I.E.P. designed the project. L.L., with help of C.H. and C.V., processed and analysed the raw data. I.E.P., M.M. and J.W. developed the physical picture with discussions from all the authors and M.M. performed the calculations. J.H.K., K.E., J.W.L. and C.B.E. grew the samples and performed the crystalline quality and transport characterizations. Y.G.C. and E.E.H. prepared the Ba-122 target for the epitaxial thin films. The paper is written by J.W., M.M. and I.E.P. with help of all the authors. J.W. coordinated the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–8, Figs. 1–12 and refs. 1–21.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Luo, L., Mootz, M., Kang, J.H. et al. Quantum coherence tomography of light-controlled superconductivity. Nat. Phys. 19, 201–209 (2023). https://doi.org/10.1038/s41567-022-01827-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01827-1
This article is cited by
-
Probing inhomogeneous cuprate superconductivity by terahertz Josephson echo spectroscopy
Nature Physics (2024)
-
Terahertz control of many-body dynamics in quantum materials
Nature Reviews Materials (2023)