Abstract
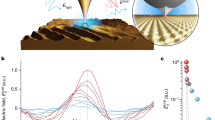
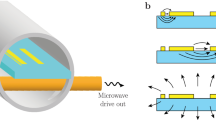
Interacting many-body systems display enhanced sensitivity close to critical transition points due to diverging quantum fluctuations. This criticality-based enhancement has been suggested as a potential resource for applications in precision metrology. Here we demonstrate many-body critical enhanced metrology for the sensing of external microwave electric fields in a non-equilibrium Rydberg atomic gas. We show that small variations in external driving lead to a large variation in the population of Rydberg states around criticality and to a notable change in the optical transmission signal. For continuous optical transmission at the critical point, we quantify the enhanced sensitivity extracting the Fisher information, which shows a three orders of magnitude increase due to many-body effects compared with single-particle systems. These results demonstrate that critical properties of many-body systems are promising resources for sensing and metrology applications.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
The data that support this study are available via GitHub56 at https://github.com/ZongkaiLiu/many-body-enhanced-metrology. Source data are provided with this paper.
References
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002).
Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).
Martin, M. J. et al. A quantum many-body spin system in an optical lattice clock. Science 341, 632–636 (2013).
Colombo, S., Pedrozo-Peñafiel, E., Adiyatullin, A.F. et al. Time-reversal-based quantum metrology with many-body entangled states. Nat. Phys. 18, 925–930. https://doi.org/10.1038/s41567-022-01653-5 (2022).
Lukin, M. D. et al. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 87, 037901 (2001).
Saffman, M., Walker, T. G. & Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 82, 2313 (2010).
Carr, C., Ritter, R., Wade, C. G., Adams, C. S. & Weatherill, K. J. Nonequilibrium phase transition in a dilute Rydberg ensemble. Phys. Rev. Lett. 111, 113901 (2013).
Ding, Dong-Sheng, Busche, H., Shi, Bao-Sen, Guo, Guang-Can & Adams, C. S. Phase diagram of non-equilibrium phase transition in a strongly-interacting Rydberg atom vapour. Phys. Rev. X 10, 021023 (2020).
Malossi, N. et al. Full counting statistics and phase diagram of a dissipative Rydberg gas. Phys. Rev. Lett. 113, 023006 (2014).
de Melo, N. R. et al. Intrinsic optical bistability in a strongly driven Rydberg ensemble. Phys. Rev. A. 93, 063863 (2016).
Šibalić, N., Wade, C. G., Adams, C. S., Weatherill, K. J. & Pohl, T. Driven-dissipative many-body systems with mixed power-law interactions: bistabilities and temperature-driven nonequilibrium phase transitions. Phys. Rev. A. 94, 011401 (2016).
Wade, C. G. et al. A terahertz-driven non-equilibrium phase transition in a room temperature atomic vapour. Nat. Commun. 9, 3567 (2018).
Wintermantel, T. M. et al. Epidemic growth and Griffiths effects on an emergent network of excited atoms. Nat. Commun. 12, 103 (2020).
Ding, D.-S. et al. Epidemic spreading and herd immunity in a driven non-equilibrium system of strongly-interacting atoms. Preprint at https://arxiv.org/abs/2106.12290 (2021).
Gibbs, H. M., McCall, S. L. & Venkatesan, T. N. C. Differential gain and bistability using a sodium-filled Fabry-Perot interferometer. Phys. Rev. Lett. 36, 1135 (1976).
Wang, H., Goorskey, D. J. & Xiao, M. Bistability and instability of three-level atoms inside an optical cavity. Phys. Rev. A. 65, 011801 (2001).
Wang, H., Goorskey, D. & Xiao, M. Enhanced Kerr nonlinearity via atomic coherence in a three-level atomic system. Phys. Rev. Lett. 87, 073601 (2001).
Pickup, L. et al. Optical bistability under nonresonant excitation in spinor polariton condensates. Phys. Rev. Lett. 120, 225301 (2018).
Hehlen, M. P. et al. Cooperative bistability in dense, excited atomic systems. Phys. Rev. Lett. 73, 1103 (1994).
Lee, T. E., Haeffner, H. & Cross, M. C. Collective quantum jumps of Rydberg atoms. Phys. Rev. Lett. 108, 023602 (2012).
Marcuzzi, M., Levi, E., Diehl, S., Garrahan, J. P. & Lesanovsky, I. Universal nonequilibrium properties of dissipative Rydberg gases. Phys. Rev. Lett. 113, 210401 (2014).
Weimer, H. Variational principle for steady states of dissipative quantum many-body systems. Phys. Rev. Lett. 114, 040402 (2015).
Levi, E., Gutiérrez, R. & Lesanovsky, I. Quantum non-equilibrium dynamics of Rydberg gases in the presence of dephasing noise of different strengths. J. Phys. B: At. Mol. Opt. Phys. 49, 184003 (2016).
Fan, H. et al. Atom based RF electric field sensing. J. Phys. B: At. Mol. Opt. Phys. 48, 202001 (2015).
Sedlacek, J. A. et al. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances. Nat. Phys. 8, 819–824 (2012).
Facon, A. et al. A sensitive electrometer based on a Rydberg atom in a Schrödinger-cat state. Nature 535, 262–265 (2016).
Cox, K. C., Meyer, D. H., Fatemi, F. K. & Kunz, P. D. Quantum-limited atomic receiver in the electrically small regime. Phys. Rev. Lett. 121, 110502 (2018).
Jing, M. et al. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat. Phys. 16, 911–915 (2020).
Liu, Zong-Kai et al. Deep learning enhanced Rydberg multifrequency microwave recognition. Nat. Commun. 13, 1997 (2022).
Gammelmark, S. & Mølmer, K. Phase transitions and Heisenberg limited metrology in an Ising chain interacting with a single-mode cavity field. New J. Phys. 13, 053035 (2011).
Macieszczak, K., Guţă, M., Lesanovsky, I. & Garrahan, J. P. Dynamical phase transitions as a resource for quantum enhanced metrology. Phys. Rev. A 93, 022103 (2016).
Fernández-Lorenzo, S. & Porras, D. Quantum sensing close to a dissipative phase transition: symmetry breaking and criticality as metrological resources. Phys. Rev. A 96, 013817 (2017).
Raghunandan, M., Wrachtrup, J. örg & Weimer, H. High-density quantum sensing with dissipative first order transitions. Phys. Rev. Lett. 120, 150501 (2018).
Garbe, L., Bina, M., Keller, A., Paris, MatteoG. A. & Felicetti, S. Critical quantum metrology with a finite-component quantum phase transition. Phys. Rev. Lett. 124, 120504 (2020).
Chu, Y., Zhang, S., Yu, B. & Cai, J. Dynamic framework for criticality-enhanced quantum sensing. Phys. Rev. Lett. 126, 010502 (2021).
Montenegro, V., Mishra, U. & Bayat, A. Global sensing and its impact for quantum many-body probes with criticality. Phys. Rev. Lett. 126, 200501 (2021).
Ilias, T., Yang, D., Huelga, S. F. & Plenio, M. B. Criticality enhanced quantum sensing via continuous measurement. PRX Quantum 3, 010354. 10.1103/PRXQuantum.3.010354 (2022).
Garbe, L., Abah, O., Felicetti, S. & Puebla, R. Critical quantum metrology with fully-connected models: from Heisenberg to Kibble-Zurek scaling. Quantum Sci. Technol. 7 035010 https://doi.org/10.1088/2058-9565/ac6ca5 (2022).
Liu, R. et al. Experimental critical quantum metrology with the Heisenberg scaling. npj Quantum Inf. 7, 170 (2021).
Zanardi, P., Paris, MatteoG. A. & Campos Venuti, L. Quantum criticality as a resource for quantum estimation. Phys. Rev. A 78, 042105 (2008).
Rossini, D. & Vicari, E. Dynamic Kibble-Zurek scaling framework for open dissipative many-body systems crossing quantum transitions. Phys. Rev. Res. 2, 023211 (2020).
Pelissetto, A., Rossini, D. & Vicari, E. Dynamic finite-size scaling after a quench at quantum transitions. Phys. Rev. E 97, 052148 (2018).
Pezzè, L., Smerzi, A., Oberthaler, M. K., Schmied, R. & Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 90, 035005 (2018).
Braunstein, S. L., Caves, C. M. & Milburn, G. J. Generalized uncertainty relations: theory, examples, and Lorentz invariance. Ann. Phys. 247, 135–173 (1996).
Zurek, W. H., Dorner, U. & Zoller, P. Dynamics of a quantum phase transition. Phys. Rev. Lett. 95, 105701 (2005).
Clark, L. W., Feng, L. & Chin, C. Universal space-time scaling symmetry in the dynamics of bosons across a quantum phase transition. Science 354, 606–610 (2016).
Keesling, A. et al. Quantum Kibble–Zurek mechanism and critical dynamics on a programmable Rydberg simulator. Nature 568, 207–211 (2019).
Trenkwalder, A. et al. Quantum phase transitions with parity-symmetry breaking and hysteresis. Nat. Phys. 12, 826–829 (2016).
Negretti, A., Henkel, C. & Mølmer, K. Quantum-limited position measurements of a dark matter-wave soliton. Phys. Rev. A 77, 043606 (2008).
Delaubert, V., Treps, N., Fabre, C., Bachor, H. A. & Réfrégier, P. Quantum limits in image processing. EPL 81, 44001 (2008).
Šibalić, N., Pritchard, J. D., Adams, C. S. & Weatherill, K. J. ARC: an open-source library for calculating properties of alkali Rydberg atoms. Comput. Phys. Commun. 220, 319–331 (2017).
Lehmann, E. L. & Casella, G. Theory of Point Estimation (Springer, 1998).
Mardia, K. V. & Marshall, R. J. Maximum likelihood estimation of models for residual covariance in spatial regression. Biometrika 71, 135–146 (1984).
Miller, K. S. Complex Stochastic Processes: An Introduction to Theory and Application (Addison Wesley Publishing Company, 1974).
Weller, D., Urvoy, A., Rico, A., Löw, R. & Kübler, H. Charge-induced optical bistability in thermal Rydberg vapor. Phys. Rev. A. 94, 063820 (2016).
Zong-Kai, L. Original data for ‘Enhanced metrology at the critical point of a many-body Rydberg atomic system’. GitHub https://github.com/ZongkaiLiu/many-body-enhanced-metrology (2022).
Acknowledgements
D.-S.D. thanks the discussions with J. Ye (JILA). Z.-K.L. appreciates the instructive discussions with T.-Y. Xie. D.-S.D. acknowledges funding from the National Key Research and Development Program of China (2017YFA0304800), the National Natural Science Foundation of China (grant no. U20A20218), the Major Science and Technology Projects in Anhui Province (grant no. 202203a13010001) and the Youth Innovation Promotion Association of the Chinese Academy of Sciences under grant no. 2018490. B.-S.S. acknowledges funding from the National Natural Science Foundation of China (grant no. 11934013), the Innovation Program for Quantum Science and Technology (2021ZD0301100) and Anhui Initiative in Quantum Information Technologies (AHY020200). C.-S.A. acknowledges funding from the EPSRC through grant agreements EP/M014398/1 (‘Rydberg Soft Matter’), EP/R002061/1 (‘Atom-based Quantum Photonics’), EP/L023024/1 (‘Cooperative Quantum Optics in Dense Thermal Vapours’), EP/P012000/1 (‘Solid State Superatoms’), EP/R035482/1 (‘Optical Clock Arrays for Quantum Metrology’) and EP/S015973/1 (‘Microwave and Terahertz Field Sensing and Imaging using Rydberg Atoms’); the Danish National Research Foundation through the Center of Excellence for Complex Quantum Systems (grant agreement no. DNRF156); DSTL; and Durham University.
Author information
Authors and Affiliations
Contributions
D.-S.D. conceived the idea and implemented the physical experiments with Z.-K.L. Z.-K.L., D.-S.D. and K.M. employed the FI. D.-S.D., Z.-K.L. and K.M. derived the equations, plotted the figures and wrote the manuscript. All the authors contributed to the discussions regarding the results and analysis contained in the manuscript. D.-S.D., B.-S.S., G.-C.G. and C.-S.A. sponsor this project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Shannon Whitlock and Abolfazl Bayat for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–4.
Supplementary Data 1
Data for Supplementary Fig. 1.
Supplementary Data 2
Data for Supplementary Fig. 2.
Supplementary Data 3
Data for Supplementary Fig. 3.
Source data
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Fig. 5
Statistical source data.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ding, DS., Liu, ZK., Shi, BS. et al. Enhanced metrology at the critical point of a many-body Rydberg atomic system. Nat. Phys. 18, 1447–1452 (2022). https://doi.org/10.1038/s41567-022-01777-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01777-8
This article is cited by
-
Criticality-enhanced electric field gradient sensor with single trapped ions
npj Quantum Information (2024)
-
Nonlinear Rydberg exciton-polaritons in Cu2O microcavities
Light: Science & Applications (2024)
-
Cavity-enhanced metrology in an atomic spin-1 Bose–Einstein condensate
Frontiers of Physics (2024)
-
Quantum metrology with boundary time crystals
Communications Physics (2023)
-
Many atoms make sensors better
Nature Physics (2022)