Abstract
In various so-called strange metals, electrons undergo Planckian dissipation1,2, a strong and anomalous scattering that grows linearly with temperature3, in contrast to the quadratic temperature dependence expected from the standard theory of metals. In some cuprates4,5 and pnictides6, a linear dependence of resistivity on a magnetic field has also been considered anomalous—possibly an additional facet of Planckian dissipation. Here we show that the resistivity of the cuprate strange metals Nd0.4La1.6−xSrxCuO4 (ref. 7) and La2−xSrxCuO4 (ref. 8) is quantitatively consistent with the standard Boltzmann theory of electron motion in a magnetic field, in all aspects—field strength, field direction, temperature and disorder level. The linear field dependence is found to be simply the consequence of scattering rate anisotropy. We conclude that Planckian dissipation is anomalous in its temperature dependence, but not in its field dependence. The scattering rate in these cuprates does not depend on field, which means that their Planckian dissipation is robust against fields up to at least 85 T.
Similar content being viewed by others
Main
The hallmark of strange metals is a perfectly linear temperature dependence of the electrical resistivity as temperature (T) goes to zero, in contrast to the T2 dependence expected from the standard Fermi-liquid theory of metals. This behaviour is observed in a wide range of metals, typically close to a quantum critical point, as in heavy-fermion metals9, hole-doped cuprates7,8, electron-doped cuprates10,11, organic superconductors12 and iron-based superconductors13,14, even though the nature of the critical point may be different15. The phenomenon is called Planckian dissipation, because in all cases an estimate1,2, or a measurement3, of the inelastic scattering time τ yields \({\tau \approx \hbar /{k_{\rm{B}}}T}\), where \({\hbar}\) is Planck’s constant and kB is Boltzmann’s constant. The microscopic mechanism that underlies Planckian dissipation remains unknown, but the simplicity and universal character of the phenomenon point to a fundamental quantum principle.
It has been suggested that the dependence of resistivity on magnetic field B is another facet of Planckian dissipation in strange metals. Specifically, the scattering rate would have not only an anomalous T-linear dependence, but also an anomalous B-linear dependence. This suggestion was inspired by the observation of B-linear resistivity in cuprates such as La2−xSrxCuO4 (LSCO)4, Tl2Ba2CuO6+δ (Tl2201) and Bi2Sr2CuO6+δ (Bi2201)5, and pnictides such as BaFe2(As1−xPx)2 (ref. 6)—a behaviour that contrasts with the usual B2 dependence observed in simple metals. In one proposal, T and B would be linked via a scattering rate of the form \({\sqrt {{\left( {\alpha {k_{\rm{B}}}T} \right)^2} + {\left( {\gamma {\mu _{\rm{B}}}B} \right)^2}}}\), where μB is the Bohr magneton, and α and γ are coefficients of comparable magnitude6.
To determine whether the linear magnetoresistance is anomalous, we must compare it to what is expected from the standard Boltzmann theory of electron motion in a magnetic field providing all electronic parameters are known. Here we carry out such a comparison in detail for two closely related strange metals: the cuprates La1.6−xNd0.4SrxCuO4 (Nd-LSCO) and LSCO, at a hole concentration (doping) of p = 0.24.
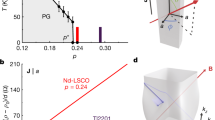
At that doping, Nd-LSCO is in its purely metallic phase, without pseudogap16,17,18, charge-density wave modulations19,20 or static magnetism21 (Fig. 1a). Its superconductivity can be entirely suppressed by applying a magnetic field in excess of 20 T. Its resistivity is perfectly T-linear down to the lowest temperature (T ≈ 1 K)7. Thermal conductivity measurements down to 50 mK have shown this T-linearity to persist down to T = 0 (ref. 22). Nd-LSCO is an archetypal strange metal, with a simple quasi-two-dimensional (2D) single-band Fermi surface, as mapped out by angle‐resolved photoemission spectroscopy (ARPES) measurements17,23.
a, Schematic temperature-doping phase diagram of the cuprate Nd-LSCO, showing the pseudogap phase (PG)16, the superconducting phase in zero field (SC), the charge-density-wave region (CDW)12,19,20 and roughly the region of strange metal behaviour (SM), distinct from the Fermi-liquid behaviour (FL). b, Temperature dependence of the in-plane resistivity ρ (J∥a) in a magnetic field B = 16 T normal to the copper oxide planes (B∥c), for our three cuprate samples, all with doping p = 0.24: Nd-LSCO (red), LSCO S1 (green) and LSCO S2 (blue). All three exhibit a perfect T-linear dependence below T ≈ 70 K, with a very similar slope. The residual resistivities extrapolated from a linear fit in the interval 20–70 K (dotted lines) are ρ0 = 28, 12 and 48 μΩ cm, respectively. The drop in ρ to zero below 10 K is due to superconductivity, not entirely suppressed at this relatively low field.
A first test of Boltzmann theory was recently carried out on Nd-LSCO in a fixed field by measuring its angle-dependent magnetoresistance (ADMR)3. Changes in the c-axis resistivity ρc as a function of the field angle relative to the c axis (θ) and a axis (ϕ) were used to extract the detailed shape and size of the Fermi surface, using the standard Chambers formalism. The resulting Fermi surface was in good agreement with that seen by ARPES, thereby validating Boltzmann theory in a fixed field.
The ADMR data were also used to extract the scattering rate 1/τ. Its T dependence was found to be linear, with a Planckian slope, namely \({1/\tau} = {\alpha {k_{\rm{B}}}{T}/\hbar}\) with α ≈ 1 (specifically, α = 1.2 ± 0.4)3. Moreover, and crucially, this T-linear inelastic scattering rate was found to be isotropic (independent of ϕ), thereby explaining how a perfect T-linear resistivity is possible in a metal whose Fermi surface, density of states and Fermi velocity are strongly anisotropic. The scattering rate is the sum of an elastic (T-independent) term and an inelastic (T-dependent) term:
Fits to the ADMR data in Nd-LSCO p = 0.24 (ref. 3) yielded the parameters α = 1.2 and, the exponent, v = 12 (Extended Data Table 1), with c = 1.0 by construction.
The strongly anisotropic elastic term in Nd-LSCO is attributed to the nearby van Hove singularity (together with small-angle scattering24), which causes the angle-dependent density of states to be strongly anisotropic, with a maximum in the antinodal directions3.
Given the Fermi surface and the scattering rate, we can now use Boltzmann theory to predict how the resistivity of Nd-LSCO should vary as a function of field strength, disorder level and field direction, at various temperatures. As shown below, we will find that all predictions are precisely confirmed by our data on Nd-LSCO and on the closely related material LSCO. In other words, the behaviour of electrons in a magnetic field in these strange metals is entirely the result of their orbital motion, and there is no evidence that the scattering rate has any field dependence.
The in-plane resistivity of the three samples considered here is displayed in Fig. 1b. It is perfectly T-linear below 70 K in all cases, with similar slopes. The only difference is the residual resistivity (at T = 0), which reflects the different levels of disorder (elastic scattering): ρ0 = 28, 12 and 48 μΩ cm for Nd-LSCO, LSCO sample S1 and LSCO sample S2, respectively.
In Fig. 2a, we display the field dependence of the in-plane resistivity ρ for Nd-LSCO, plotted as ρ(B)/ρ(0), the relative magnetoresistance (MR), obtained by applying a pulsed field up to 85 T, at various constant temperatures (the full set of isotherms is provided in Extended Data Fig. 1). In Fig. 2b, we show the corresponding prediction of Boltzmann theory, based on the parameters established by ADMR in Nd-LSCO. We see that the data and calculation are in quantitative agreement: the MR values at 4 K and 80 T are ρ(B)/ρ(0) = 1.35 and 1.30, respectively. Qualitatively, we find that the MR increases with decreasing T, and it evolves from a B2 dependence at high T to B-linear at low T—an evolution that is nicely reproduced by the calculation.
Measured and calculated MR, plotted as ρ(B)/ρ(0) versus B, for J∥a and B∥c, at various fixed temperatures, as indicated. a, Isotherms measured in Nd-LSCO up to 85 T, for T = 4 K (blue), 40 K (green) and 100 K (red). The MR at 4 K is seen to be linear in a field above ~40 T, whereas the MR at 100 K is quadratic, as emphasized by the linear (dashed) and quadratic (dashed dotted) lines. b, Calculated MR using the parameters for Nd-LSCO extracted from a previous ADMR study3, for the same three temperatures. c, Isotherms measured in LSCO S1 up to 65 T, for the same three temperatures as in a. d, Calculated MR at T = 4 K, using the full scattering rate of Nd-LSCO, given in equation (1) (red, same as in a), and using only the isotropic part of that scattering rate (blue). The parallel dashed lines are linear, to emphasize the loss of B-linearity in the isotropic case.
The B-linear dependence at low T, hailed as anomalous in previous studies, is in fact entirely accounted for by Boltzmann theory, given the strongly anisotropic elastic scattering rate of Nd-LSCO. Indeed, if we remove the anisotropic part of the scattering (by setting 1/τaniso = 0 in equation (1)), we then lose the B-linear character of the MR (Fig. 2d). The fact that the MR becomes quadratic at high T (MR ∝ B2 at 100 K) is also accounted for by the calculation (Fig. 2b), and this is due to the loss of anisotropy as the isotropic inelastic scattering dominates more and more with increasing temperature. We conclude that in overdoped Nd-LSCO and LSCO, there is no need for 1/τ to depend on the field to explain quantitatively the B-linearity, because it is simply due to the orbital motion of electrons in the presence of anisotropic impurity scattering. In other words, Planckian dissipation in these cuprates is insensitive to field, up to at least 85 T. Note that the B-linear MR observed in iron-based superconductors has also been linked to an anisotropy of the Fermi surface in those metals25.
To directly compare with earlier work on LSCO4, we also measured the field dependence of ρ in LSCO at p = 0.24, in our two samples, S1 and S2. In those two samples, ρ is T-linear below T ≈ 70 K, exactly as in Nd-LSCO, with a very similar slope (Fig. 1b). In a previous study on LSCO at p = 0.23 (ref. 8), in which a field of 48 T was applied to suppress superconductivity, the T-linear dependence of ρ was found to extend down to at least T ≈ 1 K. Note that the Fermi surface of LSCO is very similar to that of Nd-LSCO23, namely it is electron-like, because the Fermi level has crossed the van Hove singularity.
In Fig. 2c we display our high-field data on LSCO S1. The behaviour of the MR at various temperatures is seen to be very similar to that found in Nd-LSCO and in the calculations, namely B-linear at 4 K, evolving to B2 at 100 K. (Note that our MR data on LSCO are also consistent with prior MR data on LSCO p = 0.19 (ref. 4); Extended Data Fig. 2.) The only difference is the magnitude of the MR, equal to 1.65 in LSCO S1 versus 1.3 in Nd-LSCO, at 4 K and 60 T. This quantitative difference is expected, given the lower ρ0 in the former sample.
In Fig. 3a, we compare the MR in our three samples, at T = 30 K. In Fig. 3b, we show the predicted dependence of the MR on the disorder level. The calculation is performed using all the same ADMR-determined parameters, but now varying the multiplicative factor c in front of the elastic term in equation (1). By definition, c = 1.0 is the value determined by the ADMR study for an Nd-LSCO sample with a very similar ρ0 value to our own Nd-LSCO sample (from the same source and batch). We see that by decreasing the strength of disorder scattering by a factor of 0.43, namely the ratio of ρ0 values in our Nd-LSCO and LSCO S1 samples (that is, 12/28), so setting c = 0.43 in equation (1), the calculation reproduces perfectly the MR measured in sample S1. Similarly, setting c = 1.72 (that is, 48/28) yields a calculated curve in excellent agreement with the MR measured in sample S2. We conclude that Boltzmann theory is able to account very well for the effect of disorder on the magnitude of the MR in these strange metals.
a, Measured MR at T = 30 K, for Nd-LSCO (red), LSCO S1 (green) and LSCO S2 (blue). The dashed lines are linear extensions of the data. b, Calculated MR at T = 30 K, for three levels of disorder, obtained by setting the prefactor of the elastic scattering term in equation (1) to c = 1.0 (red), 0.43 (green) and 1.72 (blue). The values of c correspond to the variation in the measured ρ0 values of our three samples (Fig. 1b).
If the MR in Nd-LSCO and LSCO is entirely the result of the orbital motion of electrons around the Fermi surface, this orbital MR should all but vanish when the magnetic field is applied parallel to the CuO2 planes of the layered cuprate structure. If the materials were truly 2D, no motion could arise perpendicular to the planes and so no orbital motion could be induced by a field B∥a. These cuprates are in fact quasi-2D materials and their Fermi surface has some warping along the c axis due to a small but non-zero dispersion perpendicular to the planes, such that ρc/ρa ≈ 250 (at p = 0.24)7. In Fig. 4a, the MR predicted for Nd-LSCO is shown for B∥a at T = 50 K. A huge difference in MR between B∥c and B∥a is obtained, the latter being smaller by a factor on the order of 300 (at B = 50 T). In Fig. 4b, we display our high-field data on LSCO S1, for B∥c and B∥a. We observe a huge difference between the two field directions, with a negligible MR when B∥a. We conclude that all the field dependence of the electrical resistivity in these strange metals is coming from the orbital motion of electrons. In this respect, the earlier report of a large MR for B∥a in the cuprates Tl2201 and Bi22015—comparable to the MR for B∥c—is in striking contrast to our data and remains to be understood. Note that Boltzmann calculations for Tl2201 based on ADMR-determined parameters yield a predicted MR that is not consistent with the measured MR5. Note also that the electron-doped cuprate LCCO shows both T-linear resistivity and B-linear MR11, even though its band structure is far from a van Hove singularity and its Fermi surface is relatively isotropic. It will be interesting to measure the anisotropy of its scattering rate (this was not done in previous ADMR studies26).
a, Calculated normalized MR at T = 50 K, for a magnetic field applied parallel (red, B∥a) and perpendicular (blue, B∥c) to the CuO2 planes. b, Measured MR, ρ(B)/ρ(0), at T = 50 K, for a magnetic field applied parallel (red, B∥a) and perpendicular (blue, B∥c) to the CuO2 planes in LSCO sample S1 at p = 0.24. No MR is detected in this sample up to 50 T for B∥J∥a.
In summary, the standard Boltzmann theory accounts in detail and quantitatively for all aspects of the MR in two archetypal cuprate strange metals, including the dependence on field angle (θ and ϕ), on field strength and on disorder level, for temperatures down to T ≈ 0. Although the microscopic mechanism responsible for the perfect T-linear dependence of the resistivity in strange metals remains unknown, the strongly interacting electrons that undergo Planckian scattering nevertheless conform to the standard orbital motion in a field, as prescribed by their Fermi surface, Fermi velocity and scattering rate, the latter being independent of field. Planckian dissipation in cuprates is insensitive to magnetic field, at least up to 85 T. This contradicts a previous proposal of a B-dependent scattering rate in LSCO4.
This insensitivity to field sheds new light on the nature of scattering in cuprates. It is natural to associate the scattering process at p = 0.24 with the critical doping at which the pseudogap phase ends in Nd-LSCO, namely p* = 0.23 (ref. 16). This endpoint displays the standard thermodynamic signatures of a quantum critical point, with a sharp peak in the specific heat C versus p at p* and a log T dependence of C/T at p* (ref. 27). It was shown that, at p*, C is independent of the magnetic field up to 18 T (ref. 27). We now find that τ is independent of the field up to 85 T. This is dramatically different from the quantum criticality of other strange metals, like the heavy-fermion metals CeCu6 and CeCoIn5, where a small magnetic field strongly perturbs both the resistivity and the specific heat9,28. Clearly, the fluctuations associated with the pseudogap critical point in hole-doped cuprates, presumably responsible for the inelastic T-linear scattering near p* and potentially involved in the d-wave pairing15, are remarkably robust against magnetic fields.
Methods
Samples
Nd-LSCO
Single crystals of Nd-LSCO with a Sr content such that p = 0.24 were prepared with the floating zone technique at the University of Texas (by J.-S.Z.). A platelet sample was cut with dimensions 2 × 0.5 × 0.05 mm3 with the c axis along the shortest dimension. Longitudinal contacts were made with silver epoxy annealed in oxygen for 1 h at 500 °C. The high-symmetry crystallographic directions were determined with a precision better than 5° and they were normal to the faces of the sample. The superconducting critical temperature of this sample obtained from resistivity measurements in zero field, where ρ = 0, is Tc = 10 ± 1 K.
LSCO
Single crystals of LSCO were grown with the floating zone technique, with a Sr content such that p = 0.24. Two samples were prepared, with similar dimensions and contacts to that of our Nd-LSCO sample. LSCO sample S1 was prepared by S.O. and sample S2 by H.T. Sample S1 was annealed for several weeks in oxygen flow to reduce the oxygen deficiency, yielding a lower ρ0 compared to S2. The superconducting transition temperatures of samples S1 and S2 are Tc = 17 ± 1 K and 16 ± 1 K, respectively.
Transport measurements
Electrical d.c. resistance was measured at Sherbrooke on all samples with an in-plane excitation current in the range of 0.5–2 mA and with a steady field of 16 T applied normal to the CuO2 planes.
The longitudinal resistance was measured with a conventional four-point configuration in pulsed fields up to 85 T in Toulouse. The in-plane excitation current was 5 mA or lower, with a frequency range between 10 and ~60 kHz that was applied along the a axis in all samples.
A high-speed acquisition system was used to digitize the reference signal (current) and the voltage drop across the sample at a frequency of 500 kHz. The data were post-analysed with software to perform the phase comparison2.
MR calculations based on the Boltzmann model
All the simulations were obtained by solving the Boltzmann equation below (all further details are discussed in refs. 3,29):
where the contour integral is over the Fermi surface, D(k) is the density of state at point k, vx is the component of the Fermi velocity in the x direction, and the second integral is an integral of the Fermi velocity in the x direction that calculates the probability that a quasiparticle with lifetime τ scatters after time t. The magnetic field enters through the Lorentz force and modifies the velocity by introducing a cyclotron motion to the quasiparticles.
Data availability
Data that support the plots within this paper are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
Code availability
The code used to compute the resistivity is available from the corresponding authors upon reasonable request.
References
Bruin, J. A. N. et al. Similarity of scattering rates in metals showing T-linear resistivity. Science 339, 804–807 (2013).
Legros, A. et al. Universal T-linear resistivity and Planckian dissipation in overdoped cuprates. Nat. Phys. 15, 142–147 (2019).
Grissonnanche, G. et al. Linear-in-temperature resistivity from an isotropic Planckian scattering rate. Nature 595, 667–672 (2021).
Giraldo-Gallo, P. et al. Scale-invariant magnetoresistance in a cuprate superconductor. Science 361, 479–481 (2018).
Ayres, J. et al. Incoherent transport across the strange-metal regime of overdoped cuprates. Nature 595, 661–666 (2021).
Hayes, I. M. et al. Scaling between magnetic field and temperature in the high-temperature superconductor BaFe2 (As1-xPx)2. Nat. Phys. 12, 916–919 (2016).
Daou, R. et al. Linear temperature dependence of resistivity and change in the Fermi surface at the pseudogap critical point of a high-Tc superconductor. Nat. Phys. 5, 31–34 (2009).
Cooper, R. A. et al. Anomalous criticality in the electrical resistivity of La2−xSrxCuO4. Science 323, 603–607 (2009).
Löhneysen, H. V. et al. Non-Fermi-liquid behavior in a heavy-fermion alloy at a magnetic instability. Phys. Rev. Lett. 72, 3262–3265 (1994).
Fournier, P. et al. Insulator-metal crossover near optimal doping in Pr2−xCexCuO4: anomalous normal-state low temperature resistivity. Phys. Rev. Lett. 81, 4720–4723 (1998).
Greene, R. L. et al. The strange metal state of the electron-doped cuprates. Annu. Rev. Condens. Matter Phys. 11, 213–229 (2020).
Doiron-Leyraud, N. et al. Correlation between linear resistivity and Tc in the Bechgaard salts and the pnictide superconductor Ba(Fe1−xCox)2As2. Phys. Rev. B 80, 214531 (2009).
Kasahara, S. et al. Evolution from non-Fermi- to Fermi-liquid transport via isovalent doping in BaFe2(As1−xPx)2 superconductors. Phys. Rev. B 81, 184519 (2010).
Analytis, J. G. et al. Transport near a quantum critical point in BaFe2(As1−xPx)2. Nat. Phys. 10, 194–197 (2014).
Taillefer, L. Scattering and pairing in cuprate superconductors. Annu. Rev. Condens. Matter Phys. 1, 51–70 (2010).
Collignon, C. et al. Fermi-surface transformation across the pseudogap critical point of the cuprate superconductor La1.6−xNd0.4SrxCuO4. Phys. Rev. B 95, 224517 (2017).
Matt, C. E. et al. Electron scattering, charge order and pseudogap physics in La1.6−xNd0.4SrxCuO4: an angle-resolved photoemission spectroscopy study. Phys. Rev. B 92, 134524 (2015).
Cyr-Choinière, O. et al. Pseudogap temperature T* of cuprate superconductors from the Nernst effect. Phys. Rev. B 97, 064502 (2018).
Collignon, C. et al. Thermopower across the phase diagram of the cuprate La1.6−xNd0.4SrxCuO4: signatures of the pseudogap and charge density wave phases. Phys. Rev. B 103, 155102 (2021).
Gupta, N. K. et al. Vanishing nematic order beyond the pseudogap phase in overdoped cuprate superconductors. Proc. Natl Acad. Sci. USA 118, e2106881118 (2021).
Nachumi, B. et al. Muon spin relaxation study of the stripe phase order in La1.6−xNd0.4SrxCuO4 and related 214 cuprates. Phys. Rev. B 58, 8760–8772 (1998).
Michon, B. et al. Wiedemann-Franz law and abrupt change in conductivity across the pseudogap critical point of a cuprate superconductor. Phys. Rev. X 8, 041010 (2018).
Horio, M. et al. Three-dimensional Fermi surface of overdoped La-based cuprates. Phys. Rev. Lett. 121, 077004 (2018).
Abrahams, E. & Varma, C. M. What angle-resolved photoemission experiments tell about the microscopic theory for high-temperature superconductors. Proc. Natl Acad. Sci. USA 97, 5714–5716 (2000).
Maksimovic, N. et al. Magnetoresistance scaling and the origin of H-linear resistivity in BaFe2(As1–xPx)2. Phys. Rev. X 10, 041062 (2020).
Helm, T. et al. Magnetic breakdown in the electron-doped cuprate superconductor Nd2−xCexCuO4: the reconstructed Fermi surface survives in the strongly overdoped regime. Phys. Rev. Lett. 105, 247002 (2010).
Michon, B. et al. Thermodynamic signatures of quantum criticality in cuprate superconductors. Nature 567, 218–222 (2019).
Bianchi, A. Possible Fulde-Ferrell-Larkin-Ovchinnikov superconducting state in CeCoIn5. Phys. Rev. Lett. 91, 187004 (2003).
Fang, Y. et al. Fermi surface transformation at the pseudogap critical point of a cuprate superconductor. Nat. Phys. 18, 558–564 (2022).
Acknowledgements
We thank J. G. Analytis, R. L. Greene, N. E. Hussey, S. A. Kivelson, D. Sénéchal and B. J. Ramshaw for fruitful discussions. A portion of this work was performed at the LNCMI, a member of the European Magnetic Field Laboratory (EMFL). D.V. and C.P. acknowledge support from the EUR grant NanoX no ANR-17-EURE-0009 and from the ANR grant NEPTUN no ANR-19-CE30-0019-01. L.T. acknowledges support from the Canadian Institute for Advanced Research (CIFAR) as a Fellow and funding from the Natural Sciences and Engineering Research Council of Canada (NSERC; PIN:123817), the Fonds de recherche du Québec - Nature et Technologies (FRQNT), the Canada Foundation for Innovation (CFI) and a Canada Research Chair. This research was undertaken thanks, in part, to funding from the Canada First Research Excellence Fund. J.-S.Z. was supported by an NSF grant (MRSEC DMR-1720595). S.O. was supported by a JSPS KAKENHI grant (20H05304).
Author information
Authors and Affiliations
Contributions
A.A., A.G., S.B., J.B., L.C., M.-E.B., V.O., S.B., D.V. and C.P. performed the high-field transport measurements at LNCMI, Toulouse. A.A., A.G., F.L., N.D.-L. and S.B. performed the transport and characterization measurements at Sherbrooke. J.-S.Z. prepared the Nd-LSCO sample, S.O. prepared the LSCO S1 sample, and H.T. prepared the LSCO S2 sample. A.A. analysed the data and made the simulation figures in consultation with G.G. and L.T. A.A. and L.T. wrote the manuscript, in consultation with all the authors. L.T. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Subir Sachdev and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Field dependence of resistivity.
In-plane resistivity as a function of magnetic field (B∥a) in a) Nd-LSCO, b) LSCO sample S1 and c) LSCO sample S2, at the indicated temperatures.
Extended Data Fig. 2 Magnetoresistance in different LSCO samples.
Magnetic field dependence of the in-plane resistivity (J∥a) in LSCO at p = 0.19 (a), from4) compared with b) LSCO sample S1 and c) LSCO sample S2 at p = 0.24, at temperatures as indicated. In all cases, B∥c.
Source data
Source Data Fig. 1b
Temperature dependence of resistivity in LSCO and Nd-LSCO.
Source Data Fig. 2a
Field dependence of resistivity at various temperatures.
Source Data Fig. 2b
Calculated field dependence of resistivity at various temperatures.
Source Data Fig. 2c
Field dependence of resistivity at various temperatures.
Source Data Fig. 2d
Calculated field dependence of resistivity with different scattering rates.
Source Data Fig. 3a
Field dependence of resistivity at 30 K for different samples.
Source Data Fig. 3b
Calculated field dependence of resistivity with different disorder levels.
Source Data Fig. 4a
Calculated field dependence of resistivity for different field directions.
Source Data Fig. 4b
Field dependence of resistivity for different field directions.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ataei, A., Gourgout, A., Grissonnanche, G. et al. Electrons with Planckian scattering obey standard orbital motion in a magnetic field. Nat. Phys. 18, 1420–1424 (2022). https://doi.org/10.1038/s41567-022-01763-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01763-0
This article is cited by
-
Emergent normal fluid in the superconducting ground state of overdoped cuprates
Nature Communications (2024)