Abstract
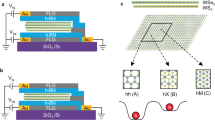
Moiré superlattices in van der Waals heterostructures have emerged as a powerful tool for engineering quantum phenomena. Here we report the observation of a correlated interlayer exciton insulator in a double-layer heterostructure composed of a WSe2 monolayer and a WS2/WSe2 moiré bilayer that are separated by ultrathin hexagonal boron nitride. The moiré WS2/WSe2 bilayer features a Mott insulator state when the density of holes is one per moiré lattice site. When electrons are added to the Mott insulator in the WS2/WSe2 moiré bilayer and an equal number of holes are injected into the WSe2 monolayer, a new interlayer exciton insulator emerges with the holes in the WSe2 monolayer and the electrons in the doped Mott insulator bound together through interlayer Coulomb interactions. The interlayer exciton insulator is stable up to a critical hole density in the WSe2 monolayer, beyond which the interlayer exciton dissociates. Our study highlights the opportunities for realizing quantum phases in double-layer moiré systems due to the interplay between the moiré flat band and strong interlayer electron interactions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper.
References
Mott, N. F. The transition to the metallic state. Philos. Mag. J. Theor. Exp. Appl. Phys. 6, 287–309 (1961).
HALPERIN, B. I. & RICE, T. M. Possible anomalies at a semimetal–semiconductor transistion. Rev. Mod. Phys. 40, 755–766 (1968).
Kuneš, J. Excitonic condensation in systems of strongly correlated electrons. J. Phys. Condens. Matter 27, 333201 (2015).
Eisenstein, J. P. Exciton condensation in bilayer quantum Hall systems. Annu. Rev. Condens. Matter Phys. 5, 159–181 (2014).
Liu, X., Watanabe, K., Taniguchi, T., Halperin, B. I. & Kim, P. Quantum Hall drag of exciton condensate in graphene. Nat. Phys. 13, 746–750 (2017).
Li, J. I. A., Taniguchi, T., Watanabe, K., Hone, J. & Dean, C. R. Excitonic superfluid phase in double bilayer graphene. Nat. Phys. 13, 751–755 (2017).
Liu, X. et al. Crossover between strongly coupled and weakly coupled exciton superfluids. Science 375, 205–209 (2022).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Chen, G. et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019).
Chen, G. et al. Signatures of tunable superconductivity in a trilayer graphene moiré superlattice. Nature 572, 215–219 (2019).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Balents, L., Dean, C. R., Efetov, D. K. & Young, A. F. Superconductivity and strong correlations in moiré flat bands. Nat. Phys. 16, 725–733 (2020).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Chen, G. et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice. Nature 579, 56–61 (2020).
Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).
Seyler, K. L. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019).
Tran, K. et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019).
Jin, C. et al. Observation of moiré excitons in WSe2/WS2 heterostructure superlattices. Nature 567, 76–80 (2019).
Alexeev, E. M. et al. Resonantly hybridized excitons in moiré superlattices in van der Waals heterostructures. Nature 567, 81–86 (2019).
Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).
Jin, C. et al. Stripe phases in WSe2/WS2 moiré superlattices. Nat. Mater. 20, 940–944 (2021).
Miao, S. et al. Strong interaction between interlayer excitons and correlated electrons in WSe2/WS2 moiré superlattice. Nat. Commun. 12, 3608 (2021).
Liu, E. et al. Excitonic and valley-polarization signatures of fractional correlated electronic phases in a WSe2/WS2 moiré superlattice. Phys. Rev. Lett. 127, 037402 (2021).
Courtade, E. et al. Charged excitons in monolayer WSe2: experiment and theory. Phys. Rev. B 96, 085302 (2017).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Li, Z. et al. Direct observation of gate-tunable dark trions in monolayer WSe2. Nano Lett. 19, 6886–6893 (2019).
Liu, E. et al. Gate tunable dark trions in monolayer WSe2. Phys. Rev. Lett. 123, 027401 (2019).
Perali, A., Neilson, D. & Hamilton, A. R. High-temperature superfluidity in double-bilayer graphene. Phys. Rev. Lett. 110, 146803 (2013).
Fogler, M. M., Butov, L. V. & Novoselov, K. S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 5, 4555 (2014).
Wu, F.-C., Xue, F. & MacDonald, A. H. Theory of two-dimensional spatially indirect equilibrium exciton condensates. Phys. Rev. B 92, 165121 (2015).
Conti, S., Neilson, D., Peeters, F. M. & Perali, A. Transition metal dichalcogenides as strategy for high temperature electron–hole superfluidity. Condens. Matter 5, 22 (2020).
Conti, S., Van der Donck, M., Perali, A., Peeters, F. M. & Neilson, D. Doping-dependent switch from one- to two-component superfluidity in coupled electron–hole van der Waals heterostructures. Phys. Rev. B 101, 220504 (2020).
Barkeshli, M., Nayak, C., Papić, Z., Young, A. & Zaletel, M. Topological exciton Fermi surfaces in two-component fractional quantized Hall insulators. Phys. Rev. Lett. 121, 026603 (2018).
Hu, Y., Venderbos, J. W. F. & Kane, C. L. Fractional excitonic insulator. Phys. Rev. Lett. 121, 126601 (2018).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Acknowledgements
This work was supported primarily by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under contract no. DE-AC02-05-CH11231 (van der Waals heterostructures programme, KCWF16). The device fabrication was also supported by the U.S. Army Research Office under MURI award W911NF-17-1-0312. E.C.R. acknowledges support from the Department of Defense through the National Defense Science and Engineering Graduate Fellowship (NDSEG) Program. S.T. acknowledges support from DOE-SC0020653, NSF CMMI 1933214, NSF mid-scale 1935994, NSF 1904716, NSF DMR 1552220 and DMR 1955889. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, grant no. PMXP0112101001, JSPS KAKENHI grant no. JP20H00354 and the CREST(JPMJCR15F3), JST.
Author information
Authors and Affiliations
Contributions
F.W. conceived the research. Z.Z. fabricated the device and performed most of the experimental measurements. E.C.R., D.W. and W.Z. contributed to the optical measurements. Z.Z. and F.W. performed data analysis. E.C.R., D.W., W.Z., S.W., M.C. and A.Z. contributed to the fabrication of van der Waals heterostructures. M.P.Z. contributed to the theory. M.S., K.Y. and S.T. grew WSe2 and WS2 crystals. K.W. and T.T. grew hBN crystals. All authors discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Andrea Perali and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Device information.
a–c, Three side-view schematics, optical microscope images, and second harmonic generation (SHG) results of Device I (a), Device II (b), and Device III (c). a, The top (bottom) hBN thickness is approximately 50 nm (50 nm). The stack is capped with an approximately 65 nm thick hBN layer. In the optical microscopy image, the dashed green (red) line outlines the WS2 (WSe2) layer in the moiré heterostructure, the dashed yellow line outlines the WSe2 monolayer, the dashed black (white) line outlines the top (bottom) FLG gate. These three flakes are aligned, as demonstrated by the SHG signal. The moiré bilayer has a near-60º twist angle. b, The top (bottom) hBN thickness is approximately 80 nm (40 nm). The stack is capped with an approximately 55 nm thick hBN layer. In the optical microscopy image, the dashed green (red) line outlines the WS2 (WSe2) layer in the moiré heterostructure, the dashed yellow line outlines the monolayer WSe2, and the dashed black line outlines the top and bottom FLG gate. The solid lines correspond to a few-layer TMDCs that are attached to the monolayers. The twist angle between the moiré bilayer and the WSe2 monolayer is around 25 degrees. The moiré bilayer has a near-zero twist angle as it shows an enhanced SHG signal. c, The stacking order of Device III is opposite to that in Device I and Device II. The moiré bilayer in device III is below the WSe2 monolayer. The top (bottom) hBN thickness is approximately 9 nm (15 nm). The stack is further capped with an approximately 8 nm thick hBN layer. In the optical microscopy image, the dashed green (red) line outlines the WS2 (WSe2) layer in the moiré heterostructure, the dashed yellow line outlines the monolayer WSe2, the dashed black (white) line outlines the top (bottom) FLG gate. The solid lines correspond to a few-layer TMDCs that are attached to the monolayers. These three layers are aligned, as determined by the SHG measurements. The moiré bilayer in device III has a near-zero twist angle.
Extended Data Fig. 2 Reflection contrast spectra of 2s exciton at four representative vertical electric fields.
a–d, The two-dimensional color plots of reflection contrast spectra at the E field of 80 mV nm−1 (a), 8 mV nm−1 (b), 0 mV nm−1 (c), and −8 mV nm−1 (d). The monolayer WSe2 2s exciton resonances at p/p0 = 1/3, 2/3, and 1 in a correspond to the generalized Wigner crystal and Mott insulator states. Prominent 2s exciton resonances are still observed at p/p0 = 1 in b–d, indicating a correlated insulating state when the total doping is at one hole per moiré superlattice site.
Extended Data Fig. 3 Mott insulator state revealed by the interlayer exciton photoluminescence.
a, The two-dimensional color plot of derivative reflection contrast spectra of 2s exciton at E = 80 mV nm−1. Well-defined and red-shifted monolayer WSe2 2s exciton resonances at p/p0 = 1 and 2 correspond to the Mott insulator and the full filling of the moiré band (that is, two holes per moiré superlattice). b, The two-dimensional color plot of interlayer exciton PL spectra of the WS2/WSe2 moiré bilayer at E = 80 mV nm−1. The PL resonance energy blueshifts suddenly, and the PL intensity exhibits a sudden increase at p/p0 = 1 and 2, which is consistent with the correlated states probed by the 2s exciton spectra. Therefore, this abrupt increase of interlayer exciton PL intensity provides a reliable signature of the Mott insulating state with one hole at each moiré superlattice (pmoiré /p0 = 1 or 2).
Extended Data Fig. 4 The trion signal at different vertical electric fields in the correlated interlayer exciton insulator.
The binding energy of the trion energy is around 21 meV.
Extended Data Fig. 5 Phase diagram of the correlated interlayer exciton insulator in device II and device III.
a and b, The WSe2 monolayer trion signal in the reflection contrast spectra (a) and WSe2 monolayer 2s exciton signal in the derivative reflection contrast spectra (b) as a function of gates’ induced hole density and vertical electric field E in device II. The dashed black line, determined by the emergence of the trion signal in a, separates region I (with a charge-neutral WSe2 monolayer) from region II (with a hole-doped WSe2 monolayer). The strongest 2s resonance at p/p0 = 1 in the region I of b defines the Mott insulator state of the moiré bilayer. This Mott insulator state becomes a correlated interlayer exciton insulator as the resonance extends to region II of b at the combined hole density p/p0 = (pmoiré +pmono) = 1. c and d, WSe2 monolayer trion signal (c) and WSe2 monolayer 2s exciton signal (d) in the derivative reflection contrast spectra function of gates’ induced hole density and vertical electric field E in device III. The dashed black line, determined by the emergence of the trion signal in c, separates region I (with a charge-neutral WSe2 monolayer) from region II (with a hole-doped WSe2 monolayer). The strongest 2s resonance in region I of c defines the Mott insulator state of the moiré bilayer. This Mott insulator state also becomes an interlayer exciton insulator as the resonance extends into region II of c with the combined hole density p/p0 = (pmoiré +pmono) = 1, and eventually disappears at the negative vertical electric field.
Extended Data Fig. 6 Line cuts of 2s exciton signal in the Mott insulator and correlated interlayer exciton insulator.
a, Reflection contrast spectra in the Mott insulator (E = 80 mV nm−1) and correlated interlayer exciton insulator (E = 0, −4, and −8 mV nm−1). b, Derivative reflection contrast spectra in the Mott insulator (E = 80 mV nm−1) and correlated interlayer exciton insulator (E = 0, −4, and −8 mV nm−1). It clearly shows that the WSe2 2s exciton feature decreases in amplitude at p/p0 = 1 with a reduced vertical electric field (increased hole doping in the WSe2 monolayer). The WSe2 2s exciton amplitudes of the interlayer exciton insulator states (E = 0, −4, and −8 mV nm−1) are weaker than that of the Mott insulator (E = 80 mV nm−1).
Extended Data Fig. 7 Line cuts of trion signal in the Mott insulator and correlated interlayer exciton insulator.
For the Mott insulator (E = 80 mV nm−1), the WSe2 monolayer does not have a trion state, while in the correlated interlayer exciton insulator state, the WSe2 monolayer does have a trion state (E = 0, −4, and −8 mV nm−1).
Extended Data Fig. 8 Estimation of critical interlayer exciton density.
a–c, WSe2 monolayer trion intensity (a), Derivative of interlayer exciton PL intensity with respect to gates induced hole density \(dI_{IX}/\left[ { - \frac{1}{e}\left( {C_{t1}V_t + C_{b1}V_b} \right)} \right]\) (b), and WSe2 monolayer 2s exciton intensity (c) as a function of the gates induced hole density \(- \frac{1}{e}\left( {C_{t1}V_t + C_{b1}V_b} \right)\) and vertical electric field E. The same figures are plotted in Fig. 3a–c, in the main text. The critical point is labeled as point X, where the correlated interlayer exciton insulator starts to melt, as shown in c. The dashed black line in a denotes states with the same trion PL intensity as, and therefore similar pmono to, the X point. The dashed green line in b corresponds to the Mott insulator in the moiré bilayer (pmoiré/p0 = 1), which is determined by the maximum of \(dI_{IX}/\left[ { - \frac{1}{e}\left( {C_{t1}V_t + C_{b1}V_b} \right)} \right]\) in b. The carrier density in the WSe2 monolayer pmono along this green dashed line can be calculated as pmono = p – pmoiré. The intersection of the dashed blue line and the dashed green line is around p/p0 = 1.5. The hole density in the WSe2 monolayer is pmono = p – pmoiré = 1.5 p0 – p0 = 0.5 p0 at the intersection. Point X should have a similar pmono because it has the same trion intensity. Therefore, the critical interlayer exciton density at point X is nX = pmono ≈ 0.5 p0.
Supplementary information
Supplementary information
Supplementary Figs. 1–9 and Sections 1–5
Supplementary Data 1
Background subtraction
Supplementary Data 2
Capacitance model
Supplementary Data 3
2s exciton signal_Vb_Vt
Supplementary Data 4
Offset estimation
Supplementary Data 5
P0 estimation
Supplementary Data 6
Gaussian fit at four E fields
Supplementary Data 7
E-dependent integrated trion area
Supplementary Data 8
P-dependent integrated trion area
Supplementary Data 9
Gaussian fit at four p doping levels
Source data
Source Data Fig. 1
Reflection contrast spectrum
Source Data Fig. 2
2s exciton, trion and IX
Source Data Fig. 3
2s exciton, trion and IX phase diagram
Source Data Fig. 4
Temperature-dependent 2s exciton
Source Data Extended Data Fig. 1
Device information
Source Data Extended Data Fig. 2
Reflection contrast spectra of 2s exciton
Source Data Extended Data Fig. 3
Mott insulator revealed by IX PL
Source Data Extended Data Fig. 4
Trion binding energy
Source Data Extended Data Fig. 5
Phase diagram of device II and III
Source Data Extended Data Fig. 6
Line cuts of 2s exciton signal
Source Data Extended Data Fig. 7
Line cuts of trion signal
Source Data Extended Data Fig. 8
Estimation of critical interlayer exciton density
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhang, Z., Regan, E.C., Wang, D. et al. Correlated interlayer exciton insulator in heterostructures of monolayer WSe2 and moiré WS2/WSe2. Nat. Phys. 18, 1214–1220 (2022). https://doi.org/10.1038/s41567-022-01702-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01702-z
This article is cited by
-
Remote imprinting of moiré lattices
Nature Materials (2024)
-
Engineering correlated insulators in bilayer graphene with a remote Coulomb superlattice
Nature Materials (2024)
-
Dynamically tunable moiré exciton Rydberg states in a monolayer semiconductor on twisted bilayer graphene
Nature Materials (2024)
-
Twistronics and moiré excitonic physics in van der Waals heterostructures
Frontiers of Physics (2024)
-
Interlayer exciton dynamics of transition metal dichalcogenide heterostructures under electric fields
Nano Research (2024)