Measurement of the Higgs boson width and evidence of its off-shell contributions to ZZ production

Abstract

Since the discovery of the Higgs boson in 2012, detailed studies of its properties have been ongoing. Besides its mass, its width—related to its lifetime—is an important parameter. One way to determine this quantity is to measure its off-shell production, where the Higgs boson mass is far away from its nominal value, and relating it to its on-shell production, where the mass is close to the nominal value. Here we report evidence for such off-shell contributions to the production cross-section of two Z bosons with data from the CMS experiment at the CERN Large Hadron Collider. We constrain the total rate of the off-shell Higgs boson contribution beyond the Z boson pair production threshold, relative to its standard model expectation, to the interval [0.0061, 2.0] at the 95% confidence level. The scenario with no off-shell contribution is excluded at a p-value of 0.0003 (3.6 standard deviations). We measure the width of the Higgs boson as ${{{\varGamma }}}_{{{{{{\rm{H}}}}}}}={3.2}_{-1.7}^{+2.4}\,{{{{{\rm{MeV}}}}}}$, in agreement with the standard model expectation of 4.1 MeV. In addition, we set constraints on anomalous Higgs boson couplings to W and Z boson pairs.

Main

The standard model (SM) of particle physics provides an elegant description for the masses and interactions of fundamental particles. These are fermions, which are the building blocks of ordinary matter, and gauge bosons, which are the carriers of the electroweak (EW) and strong forces. In addition, the SM postulates the existence of a quantum field that is responsible for the generation of the masses of fundamental particles through a phenomenon known as the Brout–Englert–Higgs mechanism. This field, known as the Higgs field^1,2,3, interacts with SM particles, giving them mass, as well as with itself. The field carrier is a massive, scalar (spin-0) particle known as the Higgs (H) boson. Nearly half a century after its postulation, it was finally observed in 2012 with a mass m_H of ~125 GeV by the ATLAS and CMS Collaborations^4,5,6 at the CERN Large Hadron Collider (LHC). Given the unique role the H boson plays in the SM, studies of its properties are a major goal of particle physics.

Apart from mass, another important property of a particle is its lifetime, τ. Only a few fundamental particles are stable. Others—including the H boson—exist only for a fleeting moment before disintegrating into other, lighter, species. The Heisenberg uncertainty principle⁷ provides a direct connection between the lifetime of a particle and the uncertainty in its mass, a property known as the particle’s width, Γ. Any unstable particle (often referred to as a resonance) has a finite lifetime, with shorter τ corresponding to broader Γ. The two quantities are related through the Planck constant, ħ, as Γ = ħ/(2πτ). Even with perfect experimental resolution, the observed mass of an unstable particle will not be constant across a series of measurements (for example, of the invariant mass of its decay products i, which is calculated from the sums of their energies, E_i, and momenta, ${{{\bf{p}}}}_{i}$, as ${\sqrt{{({\sum }_{i}{E}_{i})}^{2}-| {\sum }_{i}{{{\bf{p}}}}_{i}{| }^{2}}}$). The possible mass values are distributed according to a characteristic relativistic Breit–Wigner distribution⁸ with a nominal mass value corresponding to the maximum of the Breit–Wigner, and with width parameter Γ.

Particles are understood to be on the mass shell (on-shell) if their mass is close to the nominal mass value, and off-shell if their mass takes a value far away from it. According to the aforementioned property of the Breit–Wigner line shape, particles are generally more likely to be produced on-shell than off-shell when energy and momentum conservation allows it. Scattering amplitudes (A) for off-shell particle production, followed by a specific decay final state, may be modified further by interference with other processes, which is large and destructive in the case of the H boson. In this specific case, writing A = H + C, where H indicates the H boson contribution and C the other interfering contributions, we will use the term ‘off-shell production’ as a shorthand for the ∣H∣² term in ∣A∣².

For broad resonances, the width can be obtained by directly measuring the Breit–Wigner line shape, for example, as was done in the case of the Z boson, which was measured to have a mass of m_Z = 91.188 ± 0.002 GeV and a width of Γ_Z = 2.495 ± 0.002 GeV at the CERN Large Electron Positron collider⁹. The H boson is expected to live three orders of magnitude longer, with a theoretically predicted width of Γ_H = 4.1 MeV (0.0041 GeV)¹⁰, and a deviation from the SM prediction would indicate the existence of new physics. This width is too small to be measured directly from the line shape because of the limited mass resolution of order 1 GeV achievable with the present LHC detectors. Another direct way of measuring the H boson width would be to measure its lifetime by means of its decay length and use the relationship Γ_H = ħ/(2πτ_H), but its lifetime is still too short (τ_H = 1.6 × 10⁻²² s) to be detectable directly. The present experimental limit for this quantity is τ_H < 1.9 × 10⁻¹³ s at 95% confidence level (CL)¹¹, nine orders of magnitude above the SM lifetime.

The value of Γ_H can be extracted with much better precision through a combined measurement of on-shell and off-shell H-boson production. In the decay of an H boson with m_H ≈ 125 GeV to a pair of massive gauge bosons V (V = W or Z, with masses around 80.4 or 91.2 GeV, respectively), we have m_V < m_H < 2m_V. Therefore, when the H boson is produced on-shell (with the VV invariant mass m_VV ~ m_H), one of the V bosons must be off-shell to satisfy four-momentum conservation. Once the H boson is produced off-shell with large enough invariant mass m_VV > 2m_V (off-shell H-boson production region), the V bosons themselves are produced on-shell. Because the Breit–Wigner mass distribution of either the H or V boson maximizes at their respective nominal masses, the rate of off-shell H-boson production above the V-boson pair production threshold is enhanced with respect to what one would expect from the Breit–Wigner line shape of the H boson alone.

The measurement of the higher part of the m_VV spectrum can then be used to establish off-shell H-boson production. The ratio of off-shell to on-shell production rates allows for a measurement of Γ_H (refs. ^12,13) via the cross-section proportionality relations

$${\sigma }^{{{{{{\rm{on}}}}{\mbox{-}}{{{\rm{shell}}}}}}}\propto {\frac{{g}_{{{\rm{p}}}}^{2}{g}_{{{\rm{d}}}}^{2}}{{{{\varGamma }}}_{{{{{{\rm{H}}}}}}}}}\propto {\mu }_{{{\rm{p}}}}\Rightarrow {\sigma }^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}\propto {{g}_{{{\rm{p}}}}^{2}}{{g}_{{{\rm{d}}}}^{2}}\propto {\mu }_{{{\rm{p}}}}{{{\varGamma }}}_{{{{{{\rm{H}}}}}}},$$

where g_p and g_d are the couplings associated with the H-boson production and decay modes, respectively, and μ_p is the on-shell H-boson signal strength in the production mode being considered. Each signal strength is defined as the ratio of the H-boson squared amplitude in the measured cross-section to that predicted in the SM. The off-shell H-boson signal strength, ${\mu }_{{{\rm{p}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$, can be expressed as μ_pΓ_H in each production mode, and the scenario with no off-shell production becomes equivalent to the limiting case Γ_H = 0. For the rest of this Article, we concentrate on the ZZ decay channel, that is, g_d corresponding to the H → ZZ decay. The CMS and ATLAS Collaborations have previously used this method to set upper limits on Γ_H as low as 9.2 MeV at 95% CL^14,15.

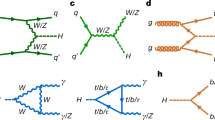
It is important to distinguish between two types of H boson production modes: the gluon fusion gg → H → ZZ process, where the H boson is produced via its couplings to fermions, and the EW processes, which involve HVV (that is, HWW or HZZ) couplings. The top row of Fig. 1 shows the Feynman diagrams for the most dominant contributions to the gg (top left) process, and the EW processes of vector boson fusion (VBF, top centre) and VH (top right). A more complete set of diagrams for the EW process is provided in Extended Data Figs. 1 and 2. Because different H-boson couplings are involved in the gg and EW processes, we extract two off-shell signal strength parameters, ${\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$ for the gg mode and ${\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$ for the EW mode. We also consider an overall off-shell signal strength parameter ${\mu }^{{\rm{off}}{\mbox{-}}{\rm{shell}}}$ with different assumptions on the ratio ${R}_{{{{{{\rm{V,F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}={\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}/{\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$.

Fig. 1: Feynman diagrams for important contributions to ZZ production.

Diagrams can be distinguished as those involving the H boson (top) and those that give rise to continuum-ZZ production (bottom). The interaction displayed at tree level in each diagram is meant to progress from left to right. Each straight, curvy or curly line refers to the different set of particles denoted. Straight, solid lines with no arrows indicate the line could refer to either a particle or an antiparticle, whereas those with forward (backward) arrows refer to a particle (an antiparticle).

A major challenge arises from the fact that there are other sources of ZZ pairs in the SM (continuum-ZZ production); see, for example, the bottom row of Fig. 1. These contributions, particularly those from ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}$, are typically much larger than the contribution from off-shell H → ZZ. In addition, some of the amplitudes from continuum-ZZ processes interfere with the H-boson amplitudes because they share the same initial and final states. For example, the amplitudes in the first column of Fig. 1, or those in the second column, interfere with each other; the amplitude shown in the lower right panel (shown more generically in Extended Data Fig. 3) does not interfere with any of the other diagrams as we omit the negligible contribution of ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{H}}}}}}\to {{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}$ that would interfere with it.

The interference between the H boson and continuum-ZZ amplitudes is destructive^{16,17,18,19,20,21}. This destructive interference plays a key role in the SM, as it is one of the contributions that unitarizes the scattering of massive gauge bosons, keeping the computation of the cross-section for ZZ production in proton–proton (pp) collisions finite^16,17,18,19. Figure 2 displays the interplay between the H-boson production modes and the interfering continuum amplitudes, illustrating the growing importance of their destructive interference as m_ZZ grows in the two final states included in the analysis, ZZ → 2ℓ2ν and ZZ → 4ℓ. In the parametrization of the total cross-section, contributions from this type of interference between the H boson and continuum-ZZ amplitudes scale as ${\sqrt{{\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}}}$ and ${\sqrt{{\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}}}$ for the gg and EW modes, respectively.

Fig. 2: SM calculations of ZZ invariant mass in the gg and EW processes.

Distributions for the 2ℓ2ν invariant mass (m_2ℓ2ν) from the gg → 2ℓ2ν process (left) and for the 4ℓ invariant mass (m_4ℓ) from the EW ZZ(→4ℓ) + qq processes (right). These processes involve the H boson (∣H∣²) and interfering continuum (∣C∣²) contributions to the scattering amplitude, as shown in black and gold, respectively. The dashed green curve represents their direct sum without interference (∣H∣² + ∣C∣²), and the solid magenta curve represents the sum with interference included (∣H + C∣²). Note that the interference is destructive, and its importance grows as the mass increases. The integrated luminosity is taken to be 1 fb⁻¹, so these distributions are equivalent to the differential cross-section spectra dσ/dm_2ℓ2ν (left) and dσ/dm_4ℓ (right). The distributions are shown after requiring that all charged leptons satisfy p_T > 7 GeV and ∣η∣ < 2.4, and that the invariant mass of any charged lepton pair with the same flavour and opposite charge is greater than 4 GeV. Here, p_T denotes the magnitude of the momentum of these leptons transverse to the pp collision axis, and η denotes their pseudorapidity, defined as $-{\ln }{\left[{\tan }\left({\theta }/{2}\right)\right]}$ using the angle θ between the momentum vector and the collision axis. Calculations for the gg → 4ℓ and EW ZZ(→2ℓ2ν) + qq processes exhibit similar qualitative properties. The details of the Monte Carlo programs used for these calculations are provided in the Methods.

In this Article we study off-shell H-boson decays to ZZ → 2ℓ2ν, and on-shell as well as off-shell H-boson decays to ZZ → 4ℓ (ℓ = μ or e), using a sample of pp collisions at 13 TeV collected by the CMS experiment at the LHC. The selection and analysis of the off-shell ZZ → 2ℓ2ν data sample is described in detail in this Article, and it is based on data collected between 2016 and 2018, corresponding to an integrated luminosity of 138 fb⁻¹. For the ZZ → 4ℓ mode, we use previously published CMS off-shell (2016 and 2017 datasets, 78 fb⁻¹; ref. ¹⁵) and on-shell (2015^15,22 and 2016–2018²³ datasets, 2.3 fb⁻¹ and 138 fb⁻¹, respectively) results.

Information on the off-shell signal strengths, Γ_H, and constraints on possible beyond-the-SM (BSM) anomalous couplings are extracted from combined fits over several kinematic distributions of the selected 2ℓ2ν and 4ℓ events. Although the off-shell events are the ones solely used to establish the presence of off-shell H-boson production, the measurement of Γ_H relies on the combination of on-shell and off-shell data.

Because of the presence of neutrinos, the H-boson mass cannot be precisely reconstructed in the H → 2ℓ2ν final state, as the longitudinal component of the total momentum carried by the neutrinos cannot be measured. Thus, on-shell information can only be extracted from the 4ℓ mode. This combination of 4ℓ and 2ℓ2ν data enables the measurement of Γ_H with a precision of ~50%. The measurement improves the upper limit on τ_H by eight orders of magnitude compared to the direct constraint from ref. ¹¹. The inclusion of the 2ℓ2ν data also allows the lower limits on ${\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$ to reach within ~65% of its best-fit value, compared to the weaker constraints from 4ℓ data alone, which reach within ~90% of the 4ℓ-only best-fit value¹⁵.

The m_ZZ line shape is sensitive to the potential presence of anomalous HVV couplings^{10,11,15,24,25,26}. Thus, BSM physics could affect the ratio of off-shell to on-shell H boson production rates, and therefore the measurement of Γ_H. We test the effect of these couplings on the Γ_H measurement and constrain the contribution from these couplings themselves. In parametrizing anomalous HVV contributions, we adopt the formalism of ref. ¹⁵ with scattering amplitude

$$\begin{array}{l}{{{{A}}}}\propto {\left[{a}_{1}-{\frac{{{q}_{1}^{2}}+{{q}_{2}^{2}}}{{{{\varLambda }}}_{1}^{2}}}\right]}{m}_{{{{{{\rm{V}}}}}}}^{2}{\epsilon }_{1}^{* }{\epsilon }_{2}^{* }\\ +{a}_{2}{f}_{\mu \nu }^{{\,}* (1)}{f}^{{\,}* (2)\mu \nu }+{a}_{3}{f}_{\mu \nu }^{{\,}* (1)}{\tilde{f}}^{{\,}* (2)\mu \nu }.\end{array}$$

Here, the polarization vector (four-momentum) of the vector boson V_i is denoted by ϵ_i (q_i), and ${f}^{{\,}(i)\mu \nu }={\epsilon }_{i}^{\mu }{q}_{i}^{\nu }-{\epsilon }_{i}^{\nu }{q}_{i}^{\mu }$ and ${\tilde{f}}_{\mu \nu }^{\,(i)}={\frac{1}{2}}{\epsilon }_{\mu \nu \rho \alpha }{f}^{\,(i)\rho \alpha }$ are tensor expressions for each V_i. The BSM couplings a₂, a₃ and ${1}/{{{\varLambda }}}_{1}^{2}$ (denoted generically as a_i) are assumed to be real and can take negative values, with the κ factors in ref. ¹⁵ absorbed into the definition of ${1}/{{{\varLambda }}}_{1}^{2}$. The first two are coefficients for generic CP-conserving and CP-violating higher-dimensional operators, respectively, while ${1}/{{{\varLambda }}}_{1}^{2}$ is the coefficient for the first-order term in the expansion of a SM-like tensor structure with an anomalous dipole form factor in the invariant masses of the two V bosons. In what follows, we will use the shorthand ‘a_i hypothesis’ to refer to the scenario where all BSM HVV couplings other than a_i itself are zero.

Throughout this work, we assume that the gluon fusion loop amplitudes do not receive new physics contributions apart from a rescaling of the SM amplitude. Possible modifications of the m_ZZ line shape^26,27 are neglected based on existing LHC constraints^28,29,30.

2ℓ2ν analysis considerations

The 2ℓ2ν analysis is based on the reconstruction of Z → ℓℓ decays with a second Z boson decaying to neutrinos that escape detection. The momentum of the undetected Z boson transverse to the pp collision axis can be measured through an imbalance across all remaining particles, that is, missing transverse momentum (${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ or ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ in vector form). Thus, the analysis requires large ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ as the Z → νν signature.

The event selection is sensitive to the tail of the instrumental ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ resolution in pp → Z + jets events, which constitute an important reducible background. This contribution is estimated through a study of a data control region (CR) of γ + jets events, where ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ is purely instrumental, as it is in Z + jets events.

Processes such as ${{{{{\rm{p}}}}}}{{{{{\rm{p}}}}}}\to {{{{{\rm{t}}}}}}\overline{{{{{{\rm{t}}}}}}}$ or WW result in non-resonant dilepton final states of the same (e⁺e⁻ and μ⁺μ⁻) and opposite (e^±μ^∓) flavour, with the same probability and the same kinematic properties. Thus, their background contribution to the 2ℓ2ν signal, which includes two leptons of the same flavour, is estimated from an opposite-flavour eμ CR.

Other backgrounds from ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}$, ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}^{\prime} \to {{{{{\rm{W}}}}}}{{{{{\rm{Z}}}}}}$ with W → ℓν and an undetected lepton, and the small contribution from tZ production, are estimated from simulation. A third CR of trilepton events, consisting mostly of ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}^{\prime} \to {{{{{\rm{W}}}}}}{{{{{\rm{Z}}}}}}$ events, is used to constrain the ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}^{\prime} \to {{{{{\rm{W}}}}}}{{{{{\rm{Z}}}}}}$ background and, most importantly, the large ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}$ background. The ability to constrain ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}$ from ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}^{\prime} \to {{{{{\rm{W}}}}}}{{{{{\rm{Z}}}}}}$ is based on the similarity in the physics of these processes.

Further details on event selection, kinematic observables and the methods to estimate the different contributions are discussed in the Methods.

2ℓ2ν kinematic observables

The analysis of off-shell H-boson events is based on m_ZZ. This quantity is computed from the reconstructed momenta in the 4ℓ final state as the invariant mass of the 4ℓ system, m_4ℓ. However, because of the undetected neutrinos, we can only use the transverse mass ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$, defined below, as a proxy for m_ZZ in the 2ℓ2ν final state. First, we identify ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ as the transverse momentum vector of the Z boson decaying into neutrinos. As there is no information on the longitudinal momenta of the neutrinos, ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$ is then computed as the invariant mass of the ZZ pair with all longitudinal momenta set to zero. This results in a variable with a distribution that peaks at m_ZZ, with a long tail towards lower values. The definition of ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$ is

$$\begin{array}{ll}{\left({m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}\right)}^{2}&={\left[\sqrt{{{p}_{{{{{{\rm{T}}}}}}}^{\ell \ell }}^{2}+{{m}_{\ell \ell }}^{2}}+\sqrt{{{p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}}^{2}+{{m}_{{{{{{\rm{Z}}}}}}}}^{2}}\right]}^{2}\\ &-{\left|{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{\ell \ell }+{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}\right|}^{2},\end{array}$$

where ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{\ell \ell }$ and m_ℓℓ are the dilepton transverse momentum and invariant mass, respectively, and m_Z, the Z boson pole mass, is taken to be 91.2 GeV.

The kinematic quantity ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ itself is used as another observable to discriminate processes with genuine, large ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ against the Z + jets background. Finally, in events with at least two jets, we use matrix element (MELA²⁶) kinematic discriminants that distinguish the VBF process from the gg process or SM backgrounds. These discriminants are the ${{{{{{\mathcal{D}}}}}}}_{2{{{{{\rm{jet}}}}}}}^{{{{{{\rm{VBF}}}}}}}$-type kinematic discriminants used in refs. ^15,23, and are based on the four-momenta of the H boson and the two jets leading in p_T.

Data interpretation

The results for the off-shell signal strength parameters ${\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$, ${\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$ and ${\mu }^{{\rm{off}}{\mbox{-}}{\rm{shell}}}$, as well as the H-boson width Γ_H, are extracted from binned extended maximum likelihood fits over several kinematic distributions following the parametrization in ref. ¹⁵. In this parametrization, all mass dependencies are absorbed into the distributions for the various terms contributing to the likelihood, and the off-shell signal strength parameters, or Γ_H, are kept mass-independent. Over different data periods and event categories, 117 multidimensional distributions are used in the fit: 42 for off-shell 2ℓ2ν data (10,867 events), including 18 distributions from the trilepton WZ CR (8,541 events), and 18 and 57 for off-shell and on-shell 4ℓ data (1,407 off-shell and 621 on-shell events), respectively.

In the 2ℓ2ν data sample, the value of ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$ is required to be greater than 300 GeV. Depending on the number of jets (N_j), this sample is binned in ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$ and ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ (N_j < 2) or ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$, ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and the ${{{{{{\mathcal{D}}}}}}}_{2{{{{{\rm{jet}}}}}}}^{{{{{{\rm{VBF}}}}}}}$-type kinematic discriminants (N_j ≥ 2). For the 4ℓ samples, the binning is in m_4ℓ and MELA discriminants, which are sensitive to differences between the H-boson signal and continuum-ZZ production, or the interfering amplitudes, or anomalous HVV couplings. These variables are listed in table II of ref. ¹⁵ for 4ℓ off-shell data, under ‘Scheme 2’ in table IV of ref. ²³ for on-shell 2016–2018 data, and in table 1 of ref. ¹⁵ for on-shell 2015 data. The m_4ℓ range is required to be within 105–140 GeV for 4ℓ on-shell data, or above 220 GeV for 4ℓ off-shell data.

Theoretical uncertainties in the kinematic distributions include the simulation of extra jets (up to 20% depending on N_j), and the quantum chromodynamic (QCD) running scale and parton distribution function (PDF) uncertainties in the cross-section calculation (up to 30% and 20%, respectively, depending on the process, and ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$ or m_4ℓ). These are particularly important in the gg process, as it cannot be constrained by the trilepton WZ CR. Theory uncertainties also include those associated with the EW corrections to the ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}$ and WZ processes, which reach 20% at masses around 1 TeV (refs. ^31,32).

Experimental uncertainties include uncertainties in the lepton reconstruction and trigger efficiency (typically 1% per lepton), the integrated luminosity (between 1.2% and 2.5%, depending on the data-taking period^33,34,35) and the jet energy scale and resolution³⁶, which affect the counting of jets, as well as the reconstruction of the VBF discriminants.

Evidence for off-shell contributions, and width measurement

A representative distribution of ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$, integrated over all N_j, is shown for 2ℓ2ν events in the left panel of Fig. 3. Finer details in terms of N_j and the various contributions to the event sample are presented in Extended Data Fig. 4. The CRs for instrumental ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and non-resonant dilepton production backgrounds are illustrated in Extended Data Figs. 5 and 6, respectively, and the CR with trilepton WZ events is illustrated in Extended Data Fig. 7. Also shown in the right panel of Fig. 3 is a representative distribution of m_4ℓ from the combined off-shell 4ℓ events.

Fig. 3: Distributions of ZZ invariant mass observables in the off-shell signal regions.

Distributions of transverse ZZ invariant mass, ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$, from the 2ℓ2ν off-shell signal region (left) and those of the 4ℓ invariant mass, m_4ℓ, from the 4ℓ off-shell signal region (right). The stacked histogram displays the distribution after a fit to the data with SM couplings, with the blue shaded area corresponding to the SM processes that do not include H-boson interactions, and the pink shaded area adding processes that include H-boson and interference contributions. The gold dot-dashed line shows the fit to the no off-shell hypothesis. The black points with error bars representing uncertainties at 68% CL show the observed data, which are consistent with the prediction with SM couplings within 1 s.d. The last bins contain the overflow. The requirements on the missing transverse momentum ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ in 2ℓ2ν events, and the ${{{{{{\mathcal{D}}}}}}}_{{{{{{\rm{bkg}}}}}}}$-type kinematic background discriminants (table II of ref. ¹⁵) in 4ℓ events are applied to enhance the H-boson signal contribution. The displayed values of integrated luminosity correspond to those included in the off-shell analyses of each final state. The bottom panels show the ratio of the data or dashed histograms to the SM prediction (stacked histogram). The black horizontal line in these panels marks unit ratio.

The constraints on ${\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$, ${\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$, ${\mu }^{{\rm{off}}{\mbox{-}}{\rm{shell}}}$ and Γ_H are summarized in Table 1, where we show the ‘observed’ results, that is, those extracted from data, as well as the ‘expected’ ones, that is, those based on the SM and our understanding of selection efficiencies, backgrounds and systematic uncertainties. The two sets of results are consistent with statistical fluctuations in the data. The constraint on Γ_H at the 95% confidence level corresponds to 7.7 × 10⁻²³ < τ_H < 1.3 × 10⁻²¹ s in the H-boson lifetime.

Table 1 Results for the off-shell signal strengths and Γ_H

The profile likelihood scans in the ${\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$ and ${\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$ plane are shown in the left panel of Fig. 4 (scans over the individual signal strengths are provided in Extended Data Fig. 8). Likelihood scans over Γ_H are displayed in the right panel of Fig. 4. These scans always include information from the 4ℓ on-shell data, and the three cases displayed correspond to adding the 4ℓ off-shell data alone, the 2ℓ2ν off-shell data alone or adding both. The steepness of the slope of the log-likelihood curves near ${\mu }^{{\rm{off}}{\mbox{-}}{\rm{shell}}}$ = 0 and Γ_H = 0 MeV is caused by the interference terms between the H-boson and continuum-ZZ production amplitudes, which scale with ${\sqrt{{\mu }^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}}}$ or ${\sqrt{{{{\varGamma }}}_{{{{{{\rm{H}}}}}}}}}$, respectively.

Fig. 4: Log-likelihood scans of ${\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$ and ${\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$, and Γ_H.

Left: two-parameter likelihood scan of the off-shell gg and EW production signal strength parameters, ${\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$ and ${\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$, respectively. The dot-dashed and dashed contours enclose the 68% $({-2}{{\Delta }}\ln {{{{L}}}}={2.30})$ and 95% $({-2}{{\Delta }}\ln {{{{L}}}}={5.99})$ CL regions. The cross marks the minimum, and the blue diamond marks the SM expectation. The integrated luminosity reaches only up to 138 fb⁻¹ as on-shell 4ℓ events are not included in performing this scan. Right: observed (solid) and expected (dashed) one-parameter likelihood scans over Γ_H. Scans are shown for the combination of 4ℓ on-shell data with 4ℓ off-shell (magenta) or 2ℓ2ν off-shell data (green) alone, or with both datasets (black). The horizontal lines indicate the 68% $({-2}{{\Delta }}\ln {{{{L}}}}={1.0})$ and 95% $({-2}{{\Delta }}\ln {{{{L}}}}={3.84})$ CL regions. The integrated luminosity reaches up to 140 fb⁻¹ as on-shell 4ℓ events are included in performing these scans. The exclusion of the no off-shell hypothesis is consistent with 3.6 s.d. in both panels.

The no off-shell scenario with ${\mu }^{{\rm{off}}{\mbox{-}}{\rm{shell}}}$ = 0, or Γ_H = 0 MeV is excluded at a p-value of 0.0003 (3.6 s.d.). The p-value calculation was checked with pseudoexperiments and the Feldman–Cousins prescription³⁷. As described in greater detail in the Methods, the exclusion is illustrated in Extended Data Fig. 9 through a comparison of the total number of events in each off-shell signal region bin predicted for the fit of the data to the no off-shell scenario, and the best fit. Constraints on Γ_H are stable within 1 MeV (0.1 MeV) for the upper (lower) limits when testing the presence of anomalous HVV couplings. More results on these anomalous couplings are discussed in the Methods and are presented in Extended Data Fig. 8 and Extended Data Table 1. All results are also tabulated in the HEPData record for this analysis³⁸.

Methods

Experimental set-up

The CMS apparatus³⁹ is a multipurpose, nearly hermetic detector, designed to trigger on⁴⁰ and identify muons, electrons, photons and charged or neutral hadrons^41,42,43. A global reconstruction algorithm, particle-flow (PF)⁴⁴, combines the information provided by the all-silicon inner tracker and by the crystal electromagnetic and brass-scintillator hadron calorimeters (ECAL and HCAL, respectively), operating inside a 3.8-T superconducting solenoid, with data from gas-ionization muon detectors interleaved with the solenoid return yoke, to build jets, missing transverse momentum, tau leptons and other physics objects^36,45,46. In the following discussion up to likelihood scans, we will focus on the details of the 2ℓ2ν analysis. Analysis details for the off-shell 4ℓ data are available in ref. ¹⁵, 2015 on-shell 4ℓ data in refs. ^15,22 and 2016–2018 on-shell 4ℓ data in ref. ²³.

Physics objects

Events in the 2ℓ2ν signal region, the eμ CR and the trilepton WZ CR are selected using single-lepton and dilepton triggers. The efficiencies of these selections are measured using orthogonal triggers, that is, jet or ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ triggers, and events triggered on a third, isolated lepton, or a jet. They range between 78% and 100%, depending on the flavour of the leptons, and p_T and η of the dilepton system, taking lower values at lower p_T. Photon triggers are used to collect events for the γ + jets CR. The photon trigger efficiency is measured using a tag-and-probe method⁴⁷ in Z → ee events, with one electron interpreted as a photon with tracks ignored, as well as through a study of ℓℓγ events. The efficiency is found to range from ~55% at 55 GeV in photon p_T to ~95% at photon p_T > 220 GeV.

Jets are reconstructed using the anti-k_T algorithm⁴⁸ with a distance parameter of 0.4. Jet energies are corrected for instrumental effects, as well as for the contribution of particles originating from additional pp interactions (pileup). A multivariate technique is used to suppress jets from pileup interactions⁴⁹. For the purpose of this analysis, we select jets of p_T > 30 GeV and ∣η∣ < 4.7, and they must be separated by ${{\Delta }}{R}={\sqrt{{({{\Delta }}\phi )}^{2}+{({{\Delta }}\eta )}^{2}}} > {0.4}$, where ϕ is the azimuthal angle (measured in radians) from a lepton or a photon of interest. Jets within ∣η∣ < 2.5 (∣η∣ < 2.4 for 2016 data) can be identified as b jets using the DeepJet algorithm⁵⁰ with a loose working point. The efficiency of this working point ranges between 75% and 95%, depending on p_T, η and the data period.

The missing transverse momentum vector ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ is estimated from the negative of the vector sum of the transverse momenta of all PF candidates. Dedicated algorithms⁵¹ are used to eliminate events featuring cosmic ray contributions, beam–gas interactions, beam halo or calorimetric noise.

The algorithms to reconstruct leptons are described in detail in ref. ⁴¹ for muons and ref. ⁴² for electrons. Muons are identified using a set of requirements on individual variables, and electrons are identified using a boosted decision tree algorithm. Leptons of interest in this analysis are expected to be isolated with respect to the activity in the rest of the event. A measure of isolation is computed from the flux of photons and hadrons reconstructed by the PF algorithm that are within a cone of ΔR < 0.3 built around the lepton direction, including corrections from the contributions of pileup. We define loose and tight isolation requirements for muons (electrons) with p_T > 5 GeV and ∣η∣ < 2.4 (∣η∣ < 2.5). The efficiency of loose selection for muons (electrons) ranges from ~85% (65–75%, depending on η) at p_T = 5 GeV to >90% (>85%) at p_T > 25 GeV. The additional requirements for tight selections reduce the efficiencies by 10–15%.

Photons are reconstructed from energy clusters in the ECAL not linked to charged tracks, with the exception of converted photons⁴². Their energies are corrected for shower containment in the ECAL crystals and energy loss due to conversions in the tracker with a multivariate regression. In this analysis, we consider photons with p_T > 20 GeV and ∣η∣ up to 2.5, with requirements on shower shape and isolation used to identify isolated photons and separate them from hadronic jets. The selection requirements are tightened in the γ + jets CR, which leads to selection efficiencies in the range 50–75%, depending on p_T and η.

Event simulation

The signal Monte Carlo (MC) samples are generated for an undecayed H boson for gg, VBF, ZH and WH productions using the POWHEG 2^52,53,54,55 program at next-to-leading order (NLO) in QCD at various H-boson pole masses ranging from 125 GeV to 3 TeV. The generated H bosons are decayed to four-fermion final states through intermediate Z bosons using the JHUGen²⁶ program, with versions between 6.9.8 and 7.4.0.

These samples are reweighted using the MELA matrix element package, which interfaces with the JHUGen and MCFM^13,56,57,58 matrix elements, following the same reweighting techniques used in ref. ¹⁵ to obtain the final ZZ event sample, including the H-boson contribution, the continuum and their interference. The MelaAnalytics package developed for ref. ¹⁵ is used to automate matrix element computations and to account for the extra partons in the NLO simulation. The gg generation is rescaled with the next-to-NLO (NNLO) QCD K-factor, differential in m_VV, and an additional uniform K-factor of 1.10 for the next-to-NNLO cross-section computed at m_H = 125 GeV (ref. ¹⁰). Furthermore, the pole mass values of the top quark (173 GeV) and the bottom quark (4.8 GeV)⁵⁹ are used in the massive loop calculations for the generation of this process. The difference that would be introduced by using the ${\overline{{{{{{\rm{MS}}}}}}}}$ renormalization scheme for these masses is found to be within systematic uncertainties after accounting for the effects on both the H-boson and continuum-ZZ amplitudes.

The tree-level Feynman diagrams in Fig. 1 illustrate the complete set contributing to the gg → ZZ process on the leftmost top and bottom panels, and some of the diagrams contributing to the EW ZZ production associated with two fermions on the middle and top right panels. Extended Data Figs. 1 and 2 display the full set of diagrams for the EW process.

The ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}$ and WZ MC samples are also generated with POWHEG 2 applying EW NLO corrections for two on-shell Z and W bosons^31,32, and NNLO QCD corrections as a function of m_VV (ref. ⁶⁰). The tree-level Feynman diagrams for these non-interfering continuum contributions are illustrated in Extended Data Fig. 3. Samples for the tZ + X processes, or other processes contributing to the CRs, are generated using MadGraph5_aMC@NLO at NLO or LO precision using the FxFx⁶¹ or MLM⁶² schemes, respectively, to match jets from matrix element calculations and parton shower.

The parton shower and hadronization are modelled with Pythia (8.205 or 8.230)⁶³, using tunes CUETP8M1⁶⁴ for the 2015 and 2016 datasets, and CP5⁶⁵ for the 2017 and 2018 periods. The PDFs are taken from NNPDF 3.0⁶⁶ with QCD orders matching those of the cross-section calculations. Finally, the detector response is simulated with the GEANT4⁶⁷ package.

Signal region selection requirements

Events in the 2ℓ2ν final state are required to have two opposite-sign, same-flavour leptons (μ⁺μ⁻ or e⁺e⁻) satisfying tight isolation requirements with p_T > 25 GeV, m_ℓℓ within 15 GeV of m_Z, and ${p}_{{{{{{\rm{T}}}}}}}^{\ell \ell } > {55}\,{{{{{\rm{GeV}}}}}}$. Additional requirements are imposed to reduce contributions from Z + jets and ${{{{{\rm{t}}}}}}\overline{{{{{{\rm{t}}}}}}}$ processes as follows. Events with b-tagged jets, additional loosely isolated leptons of p_T > 5 GeV or additional loosely identified photons with p_T > 20 GeV are vetoed. To further improve the effectiveness of the lepton veto, events with isolated reconstructed tracks of p_T > 10 GeV are removed. This requirement is also effective against one-prong τ decays.

The value of ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ is required to be >125 GeV (>140 GeV) for N_j < 2 (≥2). Requirements are imposed on the unsigned azimuthal opening angles (Δϕ) between ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and other objects in the event to reduce contamination from ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ misreconstruction: ${{\Delta }}{\phi }_{{{{{{\rm{miss}}}}}}}^{\ell \ell } > {1.0}$ between ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{\ell \ell }$, ${{\Delta }}{\phi }_{{{{{{\rm{miss}}}}}}}^{\ell \ell {{{{{\rm{+jets}}}}}}} > {2.5}$ between ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{\ell \ell }+{\sum }{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{j}}}}}}}$, $\min {{\Delta }}{\phi }^{{{\mathrm{j}}}}_{{{\mathrm{miss}}}} > 0.25$ (0.50) between ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{j}}}}}}}$ for N_j = 1 (N_j ≥ 2), where ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{j}}}}}}}$ is the transverse momentum vector of a jet.

Finally, events are split into lepton flavour (μμ or ee) and jet multiplicity (N_j = 0, 1, ≥2) categories. The resulting event distributions are illustrated along the ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$ observable in Extended Data Fig. 4.

Matrix element kinematic discriminants

In events with N_j ≥ 2, we use two MELA kinematic discriminants for the VBF process, ${{{{{{\mathcal{D}}}}}}}_{2{{{{{\rm{jet}}}}}}}^{{{{{{\rm{VBF}}}}}}}$ and ${{{{{{\mathcal{D}}}}}}}_{2{{{{{\rm{jet}}}}}}}^{{{{{{\rm{VBF}}}}}},\,{a2}}$ (ref. ¹⁵). Each of these discriminants consists of a ratio of two matrix elements or, equivalently, a ratio of event-by-event probability functions, expressed in terms of the four-momenta of the H boson and the two jets leading in p_T. The four-momentum of the H boson in the 2ℓ2ν channel is approximated by taking the η of the Z → 2ν candidate, together with its sign, to be the same as that of the Z → 2ℓ candidate. This approximation is found to be adequate through MC studies.

In both discriminants, one of the matrix elements is always computed for the SM H-boson production through gluon fusion. The remaining matrix element is computed for the SM VBF process in ${{{{{{\mathcal{D}}}}}}}_{2{{{{{\rm{jet}}}}}}}^{{{{{{\rm{VBF}}}}}}}$, so this discriminant improves the sensitivity to the EW H-boson production. The ${{{{{{\mathcal{D}}}}}}}_{2{{{{{\rm{jet}}}}}}}^{{{{{{\rm{VBF}}}}}},\,{a2}}$ discriminant also computes the remaining matrix element for the VBF process, but under the a₂ HVV coupling hypothesis instead of the SM scenario. We find that this second discriminant brings additional sensitivity to SM backgrounds as well as being sensitive to the a₂ HVV coupling hypothesis by design. When anomalous HVV contributions are considered, the a₂ hypothesis used in the computation is replaced by the appropriate a_i hypothesis to optimize the sensitivity for the coupling of interest.

Control regions

As already mentioned, Z + jets events are a background to the 2ℓ2ν signal selection. This can occur because of resolution effects in ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and the large cross-section for this process. Because γ + jets and Z + jets have similar production and ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ resolution properties, the Z + jets contributions at high ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ can be estimated from a γ + jets CR⁶⁸.

In this CR, all event selection requirements are the same as those on the signal region, except that the photon replaces the Z → ℓℓ decay. The ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}}$ kinematic variable is constructed using the photon p_T in place of ${p}_{{{{{{\rm{T}}}}}}}^{\ell \ell }$, and m_Z in place of m_ℓℓ. Only photons in the barrel region (that is, ∣η∣ < 1.44) are considered for N_j < 2 to eliminate beam halo events that can mimic the ${\gamma }+{p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ signature. Reweighting factors are extracted as a function of photon p_T, photon η (when N_j ≥ 2) and the number of observed pp collisions by matching the corresponding distributions in γ + jets sidebands at low ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ (<125 GeV) to those of Z + jets sidebands with the same requirement at each N_j category separately. These reweighting factors are then applied to the high-${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ γ + jets data sample. This technique to estimate the background from the data is verified using closure tests from the simulation by comparing the Z + jets and reweighted γ + jets MC distributions over each kinematic observable.

Contributions to the γ + jets CR from events with genuine, large ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ from the Z(→νν)γ, W(→ℓν)γ and W(→ℓν) + jets processes are subtracted in the final estimate of the instrumental ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ background. The first two are estimated from simulation, where the Zγ contribution is corrected based on the observed rate of Z(→ℓℓ)γ. The W + jets contribution is estimated from a single-electron sample selected with requirements similar to those in the γ + jets CR. Representative distributions for this estimate are shown in Extended Data Fig. 5.

Processes such as ${{{{{\rm{p}}}}}}{{{{{\rm{p}}}}}}\to {{{{{\rm{t}}}}}}\overline{{{{{{\rm{t}}}}}}}$ and pp → WW, including non-resonant H-boson contributions, can produce two leptons and large ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ without a resonant Z → ℓℓ decay. The kinematic properties of the dilepton system in these processes are the same for any combination of lepton flavours e or μ. These non-resonant ee or μμ background processes are therefore estimated from an eμ CR. This CR is constructed by applying the same requirements used in the signal selection except for the flavour of the leptons. Data events are reweighted to account for differences in trigger and reconstruction efficiencies between eμ, and ee or μμ final states. Representative distributions for this estimate are shown in Extended Data Fig. 6.

A third CR selects trilepton ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{W}}}}}}{{{{{\rm{Z}}}}}}$ events. These events are used to constrain the normalization and kinematic properties of the ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{{{{{\rm{Z}}}}}}$ and WZ continuum contributions. The Z → ℓℓ candidate is identified from the opposite-sign, same-flavour lepton pair with m_ℓℓ closest to m_Z, and the value of m_ℓℓ for this Z candidate is required to be within 15 GeV of m_Z. Trigger requirements are only placed on this Z candidate. The remaining lepton is identified as the lepton from the W decay (ℓ_W). The leading-p_T lepton from the Z decay is required to satisfy p_T > 30 GeV, and the remaining leptons are required to satisfy p_T > 20 GeV.

Similar to the signal region, requirements are imposed on the unsigned Δϕ between ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and other objects in the event so as to reduce contamination from the Z + jets and ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{\gamma}$ processes: ${{\Delta }}{\phi }_{{{{{{\rm{miss}}}}}}}^{\ell \ell } > {1.0}$ between ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{\ell \ell }$ for the Z candidate, ${{\Delta }}{\phi }_{{{{{{\rm{miss}}}}}}}^{3\ell {{{{{\rm{+jets}}}}}}} > {2.5}$ between ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{3\ell }+{\sum }{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{j}}}}}}}$, and $\min {{\Delta }{\phi }^{{\mathrm{j}}}_{{\mathrm{miss}}}} > 0.25$ between ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and ${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{j}}}}}}}$.

The W-boson transverse mass is defined through the vector transverse momentum of ℓ_W (${{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}}$) as ${m}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}}={\sqrt{2({p}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}}{p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}-{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}}\cdot {{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}})}}$, and additional requirements are imposed on ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}$ and ${m}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}}$ to reduce contamination from the Z + jets and ${{{{{\rm{q}}}}}}\overline{{{{{{\rm{q}}}}}}}\to {{{{{\rm{Z}}}}}}{\gamma}$ processes further: ${p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}} > {20}\,{{{{{\rm{GeV}}}}}}$, ${m}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}} > {20}\,{{{{{\rm{GeV}}}}}}$ (10 GeV) for ℓ_W = μ (e), and ${{{{A}}}}\, {m}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}}+{p}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}} > {120}\,{{{{{\rm{GeV}}}}}}$, with A = 1.6 (4/3) for ℓ_W = μ (e). All other requirements on b-tagged jets, and additional leptons or photons are the same as those for the signal region.

The events are finally split into categories of the flavour of ℓ_W (μ or e) and jet multiplicity (N_j = 0, 1, ≥2), and binned in ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{W}}}}}}{{{{{\rm{Z}}}}}}}$, defined using the W-boson mass m_W = 80.4 GeV (ref. ⁵⁹) as

$$\begin{array}{ll}{\left({m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{W}}}}}}{{{{{\rm{Z}}}}}}}\right)}^{2}&=\left[\sqrt{{{p}_{{{{{{\rm{T}}}}}}}^{\ell \ell }}^{2}+{{m}_{\ell \ell }}^{2}}\right.\\ &{\left.+\sqrt{{\left|{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}+{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}}\right|}^{2}+{{m}_{{{{{{\rm{W}}}}}}}}^{2}}\right]}^{2}\\ &-{\left|{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{\ell \ell }+{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{miss}}}}}}}+{{{\bf{p}}}}_{{{{{{\rm{T}}}}}}}^{{\ell }_{{{{{{\rm{W}}}}}}}}\right|}^{2}.\end{array}$$

Event distributions along ${m}_{{{{{{\rm{T}}}}}}}^{{{{{{\rm{W}}}}}}{{{{{\rm{Z}}}}}}}$ from this CR are shown in Extended Data Fig. 7.

Likelihood scans

As mentioned in the discussion of data interpretation, the likelihood is constructed from several multidimensional distributions binned over the different event categories. Profile likelihood scans over ${\mu }_{{{{{{\rm{F}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$, ${\mu }_{{{{{{\rm{V}}}}}}}^{{{{{{\rm{off}}}}{\mbox{-}}{{{\rm{shell}}}}}}}$,${\mu}^{{\rm{off}}{\mbox{-}}{\rm{shell}}}$ and Γ_H are shown in Extended Data Fig. 8. When testing the effects of anomalous HVV couplings, we perform fits to the data with all BSM couplings set to zero, except the one being tested, in the model to be fit. Because the only remaining degree of freedom is the ratio of these BSM couplings to the SM-like coupling, a₁, the probability densities are parametrized in terms of the effective, signed on-shell cross-section fraction f_ai for each a_i coupling, where the sign of the phase of a_i relative to a₁ is absorbed into the definition of f_ai (ref. ²³). The constraints on Γ_H are found to be stable within 1 MeV (0.1 MeV) for the upper (lower) limits under the different anomalous HVV coupling conditions, and they are summarized in Extended Data Table 1.

In addition, we provide a simplified illustration of the exclusion of the no off-shell hypothesis (Extended Data Fig. 9). In this figure, the total numbers of events in each bin of the likelihood are compared for the 2ℓ2ν and 4ℓ off-shell regions for the fit of the data to the no off-shell (N_{no off-shell}) scenario, and the best fit (N_{best fit}). Events can then be rebinned over the ratio N_{no off-shell}/(N_{no off-shell} + N_{best fit}) extracted from each bin, and these rebinned distributions can then be compared at different Γ_H values. In particular, we compare the observed and expected event distributions over this ratio under the best-fit scenario, and the scenario with no off-shell H-boson production, to illustrate which bins bring most sensitivity to the exclusion of the no off-shell scenario. The exclusion is noted to be most apparent from the last two bins displayed in this figure. We note, however, that the full power of the analysis ultimately comes from the different bins over the multidimensional likelihood, and that this figure only serves to condense the information for illustration.

When we perform separate likelihood scans over the three f_ai fractions, only the corresponding BSM parameter is allowed to be non-zero in the fit. Profile likelihood scans for f_a2, f_a3 and f_Λ1 under different fit conditions are shown in Extended Data Fig. 8, and a summary of the allowed intervals at 68% and 95% CL is presented in Extended Data Table 1.