Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

A universal qudit quantum processor with trapped ions

Nature Physics volume 18, pages 1053–1057 (2022)Cite this article

Subjects

Abstract

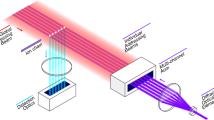
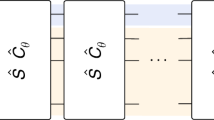
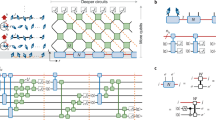
Most quantum computers use binary encoding to store information in qubits—the quantum analogue of classical bits. Yet, the underlying physical hardware consists of information carriers that are not necessarily binary, but typically exhibit a rich multilevel structure. Operating them as qubits artificially restricts their degrees of freedom to two energy levels1. Meanwhile, a wide range of applications—from quantum chemistry2 to quantum simulation3—would benefit from access to higher-dimensional Hilbert spaces, which qubit-based quantum computers can only emulate4. Here we demonstrate a universal quantum processor using trapped ions that act as qudits with a local Hilbert-space dimension of up to seven. With a performance similar to qubit quantum processors5, this approach enables the native simulation of high-dimensional quantum systems3, as well as more efficient implementation of qubit-based algorithms6,7.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Level scheme of the 40Ca+ ion.
Fig. 2: Single-qudit randomized benchmarking in an eight-ion register.
Fig. 3: Qutrit entangling gates in an eight-ion register.
Fig. 4: Full qudit readout.

Data availability

Source data are provided with this paper. The data underlying this work are available via Zenodo at https://doi.org/10.5281/zenodo.6527605.

Code availability

All the codes used for data analysis are available from the corresponding author upon reasonable request.

References

  1. Schindler, P. et al. A quantum information processor with trapped ions. New J. Phys. 15, 123012 (2013).

    Article  ADS  Google Scholar 

  2. MacDonell, R. J. et al. Analog quantum simulation of chemical dynamics. Chem. Sci. 12, 9794–9805 (2021).

    Article  Google Scholar 

  3. Rico, E. et al. SO(3) ‘nuclear physics’ with ultracold gases. Ann. Phys. 393, 466–483 (2018).

  4. Bullock, S., O’Leary, D. & Brennen, G. Asymptotically optimal quantum circuits for d-level systems. Phys. Rev. Lett. 94, 230502 (2005).

    Article  ADS  Google Scholar 

  5. Bermudez, A. et al. Assessing the progress of trapped-ion processors towards fault-tolerant quantum computation. Phys. Rev. X 7, 041061 (2017).

    Google Scholar 

  6. Lanyon, B. P. et al. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nat. Phys. 5, 134–140 (2008).

    Article  Google Scholar 

  7. Wang, Y., Hu, Z., Sanders, B. C. & Kais, S. Qudits and high-dimensional quantum computing. Front. Phys. 8, 589504 (2020).

    Article  Google Scholar 

  8. Martinez, E. A. et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 534, 516–519 (2016).

    Article  ADS  Google Scholar 

  9. Senko, C. et al. Realization of a quantum integer-spin chain with controllable interactions. Phys. Rev. X 5, 021026 (2015).

    Google Scholar 

  10. Leupold, F. M. et al. Sustained state-independent quantum contextual correlations from a single ion. Phys. Rev. Lett. 120, 180401 (2018).

    Article  ADS  Google Scholar 

  11. Malinowski, M. et al. Probing the limits of correlations in an indivisible quantum system. Phys. Rev. A 98, 050102 (2018).

    Article  ADS  Google Scholar 

  12. Ahn, J., Weinacht, T. & Bucksbaum, P. Information storage and retrieval through quantum phase. Science 287, 463–465 (2000).

    Article  ADS  Google Scholar 

  13. Godfrin, C. et al. Operating quantum states in single magnetic molecules: implementation of Grover’s quantum algorithm. Phys. Rev. Lett. 119, 187702 (2017).

    Article  ADS  Google Scholar 

  14. Anderson, B. E., Sosa-Martinez, H., Riofrío, C. A., Deutsch, I. H. & Jessen, P. S. Accurate and robust unitary transformations of a high-dimensional quantum system. Phys. Rev. Lett. 114, 240401 (2015).

    Article  ADS  Google Scholar 

  15. Morvan, A. et al. Qutrit randomized benchmarking. Phys. Rev. Lett. 126, 210504 (2021).

    Article  ADS  Google Scholar 

  16. Hu, X.-M. et al. Beating the channel capacity limit for superdense coding with entangled ququarts. Sci. Adv. 4, eaat9304 (2018).

    Article  ADS  Google Scholar 

  17. Weggemans, J. R. et al. Solving correlation clustering with QAOA and a Rydberg qudit system: a full-stack approach. Quantum 6, 687 (2022).

    Article  Google Scholar 

  18. Kasper, V. et al. Universal quantum computation and quantum error correction with ultracold atomic mixtures. Quantum Sci. Technol. 7, 015008 (2022).

    Article  ADS  Google Scholar 

  19. Ringbauer, M. et al. Certification and quantification of multilevel quantum coherence. Phys. Rev. X 8, 041007 (2018).

    Google Scholar 

  20. Kraft, T., Ritz, C., Brunner, N., Huber, M. & Gühne, O. Characterizing genuine multilevel entanglement. Phys. Rev. Lett. 120, 060502 (2018).

    Article  ADS  Google Scholar 

  21. Scott, A. J. Multipartite entanglement, quantum-error-correcting codes, and entangling power of quantum evolutions. Phys. Rev. A 69, 052330 (2004).

    Article  ADS  Google Scholar 

  22. Shlyakhov, A. R. et al. Quantum metrology with a transmon qutrit. Phys. Rev. A 97, 022115 (2018).

    Article  ADS  Google Scholar 

  23. Kristen, M. et al. Amplitude and frequency sensing of microwave fields with a superconducting transmon qudit. npj Quantum Inf. 6, 57 (2020).

    Article  ADS  Google Scholar 

  24. Huber, M. & de Vicente, J. I. Structure of multidimensional entanglement in multipartite systems. Phys. Rev. Lett. 110, 030501 (2013).

    Article  ADS  Google Scholar 

  25. Campbell, E. T. Enhanced fault-tolerant quantum computing in d-level systems. Phys. Rev. Lett. 113, 230501 (2014).

    Article  ADS  Google Scholar 

  26. Campbell, E. T., Anwar, H. & Browne, D. E. Magic-state distillation in all prime dimensions using quantum Reed-Muller codes. Phys. Rev. X 2, 041021 (2012).

  27. Joshi, M. K. et al. Polarization-gradient cooling of 1D and 2D ion Coulomb crystals. New J. Phys. 22, 103013 (2020).

    Article  ADS  Google Scholar 

  28. Barenco, A. et al. Elementary gates for quantum computation. Phys. Rev. A 52, 3457–3467 (1995).

    Article  ADS  Google Scholar 

  29. Sorensen, A. & Molmer, K. Entanglement and quantum computation with ions in thermal motion. Phys. Rev. A 62, 022311 (2000).

    Article  ADS  Google Scholar 

  30. Brennen, G. K., Bullock, S. S. & O’Leary, D. P. Efficient circuits for exact-universal computations with qudits. Quantum Inf. Comput. 6, 436–454 (2005).

    MathSciNet  MATH  Google Scholar 

  31. Gell-Mann, M. Symmetries of baryons and mesons. Phys. Rev. 125, 1067–1084 (1962).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Gottesman, D. Theory of fault-tolerant quantum computation. Phys. Rev. A 57, 127–137 (1998).

    Article  ADS  Google Scholar 

  33. Clark, S. Valence bond solid formalism for d-level one-way quantum computation. J. Phys. A 39, 2701–2721 (2006).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. Howard, M. & Vala, J. Qudit versions of the qubit π/8 gate. Phys. Rev. A 86, 022316 (2012).

    Article  ADS  Google Scholar 

  35. Magesan, E., Gambetta, J. M. & Emerson, J. Characterizing quantum gates via randomized benchmarking. Phys. Rev. A 85, 042311 (2012).

    Article  ADS  Google Scholar 

  36. Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).

    Article  ADS  Google Scholar 

  37. Low, P. J., White, B. M., Cox, A. A., Day, M. L. & Senko, C. Practical trapped-ion protocols for universal qudit-based quantum computing. Phys. Rev. Res. 2, 033128 (2020).

    Article  Google Scholar 

  38. Pogorelov, I. et al. Compact ion-trap quantum computing demonstrator. PRX Quantum 2, 020343 (2021).

    Article  ADS  Google Scholar 

  39. Parrado-Rodríguez, P., Ryan-Anderson, C., Bermudez, A. & Müller, M. Crosstalk suppression for fault-tolerant quantum error correction with trapped ions. Quantum 5, 487 (2021).

    Article  Google Scholar 

  40. Kim, S.: Acousto-Optic Devices for Optical Signal Processing and Quantum Computing. Dissertation, University of Colorado (2008).

  41. Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63–66 (2016).

    Article  ADS  Google Scholar 

  42. Häffner, H. et al. Precision measurement and compensation of optical Stark shifts for an ion-trap quantum processor. Phys. Rev. Lett. 90, 143602 (2003).

    Article  ADS  Google Scholar 

  43. O’Leary, D. P., Brennen, G. K. & Bullock, S. S. Parallelism for quantum computation with qudits. Phys. Rev. A 74, 032334 (2006).

    Article  ADS  Google Scholar 

  44. Ringbauer, M. et al. Characterizing quantum dynamics with initial system-environment correlations. Phys. Rev. Lett. 114, 090402 (2015).

    Article  ADS  Google Scholar 

  45. Ferrie, C. & Blume-Kohout, R. Estimating the bias of a noisy coin. AIP Conf. Proc. 1443, 14–21 (2012).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank M. Huber and J. Wallman for discussions. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 840450. It reflects only the author’s view; the EU Agency is not responsible for any use that may be made of the information it contains. We also acknowledge support by the Austrian Science Fund (FWF), through the SFB BeyondC (FWF project no. F7109); by the Institut für Quanteninformation GmbH; by the US Army Research Office (ARO) through grant no. W911NF-21-1-0007; by the US Air Force Office of Scientific Research (AFOSR) via IOE grant no. FA9550-19-1-7044 LASCEM; and by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via the US ARO grant no. W911NF-16-1-0070. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 801110 and the Austrian Federal Ministry of Education, Science and Research (BMBWF).

Author information

Authors and Affiliations

  1. Institut für Experimentalphysik, Universität Innsbruck, Innsbruck, Austria

    Martin Ringbauer, Michael Meth, Lukas Postler, Roman Stricker, Rainer Blatt, Philipp Schindler & Thomas Monz

  2. Institut für Quantenoptik und Quanteninformation, Österreichische Akademie der Wissenschaften, Innsbruck, Austria

    Rainer Blatt

  3. Alpine Quantum Technologies GmbH, Innsbruck, Austria

    Rainer Blatt & Thomas Monz

Authors
  1. Martin Ringbauer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael Meth
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lukas Postler
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Roman Stricker
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Rainer Blatt
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Philipp Schindler
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Thomas Monz
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.R. developed the concepts. M.R., M.M., L.P., R.S., P.S. and T.M. performed the experiments. M.R. analyzed the data. T.M. and R.B. supervised the project. All the authors contributed to writing the manuscript.

Corresponding author

Correspondence to Martin Ringbauer.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Winfried Hensinger and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Discussion 1–8, Figs. 1–11, Tables 1 and 2, and Algorithm 1.

Source data

Source Data Fig. 2

Statistical source data.

Source Data Fig. 3a

Statistical source data.

Source Data Fig. 3b

Statistical source data.

Source Data Fig. 4

Statistical source data.

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ringbauer, M., Meth, M., Postler, L. et al. A universal qudit quantum processor with trapped ions. Nat. Phys. 18, 1053–1057 (2022). https://doi.org/10.1038/s41567-022-01658-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01658-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing