Abstract
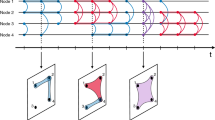
Identifying the hidden organizational principles and relevant structures of complex networks is fundamental to understand their properties. To this end, uncovering the structures involving the prominent nodes in a network is an effective approach. In temporal networks, the simultaneity of connections is crucial for temporally stable structures to arise. Here, we propose a measure to quantitatively investigate the tendency of well-connected nodes to form simultaneous and stable structures in a temporal network. We refer to this tendency as the temporal rich club phenomenon, characterized by a coefficient defined as the maximal value of the density of links between nodes with a minimal required degree, which remain stable for a certain duration. We illustrate the use of this concept by analysing diverse data sets and their temporal properties, from the role of cohesive structures in relation to processes unfolding on top of the network to the study of specific moments of interest in the evolution of the network.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All the data used in this work are available at https://github.com/nicolaPedre/Temporal-Rich-Club/.
Code availability
The analysis presented here were performed in Python. Example notebooks are available at https://github.com/nicolaPedre/Temporal-Rich-Club/.
The randomized reference models were obtained thanks to the publicly available notebooks by the authors of ref. 34, namely at https://github.com/mgenois/RandTempNet.
References
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002).
Dorogovtsev, S. N. & Mendes, J. F. F. Evolution of Networks: from Biological Nets to the Internet and WWW (Oxford Univ. Press, 2003).
Barrat, A., Barthelemy, M. & Vespignani, A. Dynamical Processes on Complex Networks (Cambridge Univ. Press, 2008).
Flake, G., Lawrence, S., Giles, C. & Coetzee, F. Self-organization and identification of web communities. Computer 35, 66–70 (2002).
Barrat, A., Barthélemy, M., Pastor-Satorras, R. & Vespignani, A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. U. S. A. 101, 3747–3752 (2004).
Barabási, A.-L. & Oltvai, Z. N. Network biology: understanding the cell’s functional organization. Nat. Rev. Genet. 5, 101–113 (2004).
Maslov, S. & Sneppen, K. Specificity and stability in topology of protein networks. Science 296, 910–913 (2002).
Pilosof, S., Porter, M. A., Pascual, M. & Kéfi, S. The multilayer nature of ecological networks. Nat. Ecol. Evol. 1, 0101 (2017).
Bullmore, E. & Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009).
Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998).
Cattuto, C. et al. Dynamics of person-to-person interactions from distributed RFID sensor networks. PLOS ONE 5, 1–9 (2010).
Stehlé, J. et al. High-resolution measurements of face-to-face contact patterns in a primary school. PLOS ONE 6, 1–13 (2011).
Rombach, M. P., Porter, M. A., Fowler, J. H. & Mucha, P. J. Core–periphery structure in networks. SIAM J. Appl. Math. 74, 167–190 (2014).
Alvarez-Hamelin, J. I., Dall’Asta, L., Barrat, A. & Vespignani, A. K-core decomposition of Internet graphs: hierarchies, self-similarity and measurement biases. Netw. Heterog. Media 3, 371 (2008).
Kitsak, M. et al. Identification of influential spreaders in complex networks. Nat. Phys. 6, 888–893 (2010).
Zhou, S. & Mondragon, R. The rich-club phenomenon in the internet topology. IEEE Commun. Lett. 8, 180–182 (2004).
Colizza, V., Flammini, A., Serrano, M. A. & Vespignani, A. Detecting rich-club ordering in complex networks. Nat. Phys. 2, 110–115 (2006).
Opsahl, T., Colizza, V., Panzarasa, P. & Ramasco, J. J. Prominence and control: the weighted rich-club effect. Phys. Rev. Lett. 101, 168702 (2008).
Serrano, M. A. Rich-club vs rich-multipolarization phenomena in weighted networks. Phys. Rev. E 78, 026101 (2008).
McAuley, J. J., da Fontoura Costa, L. & Caetano, T. S. Rich-club phenomenon across complex network hierarchies. Appl. Phys. Lett. 91, 084103 (2007).
Zhou, S. & Mondragón, R. Structural constraints in complex networks. N. J. Phys. 9, 173 (2007).
van den Heuvel, M. P. & Sporns, O. Rich-club organization of the human connectome. J. Neurosci. 31, 15775–15786 (2011).
Holme, P. & Saramäki, J. Temporal networks. Phys. Rep. 519, 97–125 (2012).
Holme, P. Modern temporal network theory: a colloquium. Eur. Phys. J. B 88, 234 (2015).
Holme, P. & Saramäki, J. (eds.) Temporal Network Theory (Springer, 2019).
Braha, D. & Bar-Yam, Y. From centrality to temporary fame: dynamic centrality in complex networks. Complexity 12, 59–63 (2006).
Braha, D. & Bar-Yam, Y. in Adaptive Networks, vol. 51 of Understanding Complex Systems (eds Gross, T. & Sayama, H.) pp 39–50 (Springer, 2009).
Pedreschi, N. et al. Dynamic core-periphery structure of information sharing networks in entorhinal cortex and hippocampus. Netw. Neurosci. 4, 946–975 (2020).
Masuda Naoki, M. J. C. & Petter, H. Concurrency measures in the era of temporal network. J. R. Soc. Interface. 18, 20210019 (2021).
Kovanen, L., Karsai, M., Kaski, K., Kertész, J. & Saramäki, J. Temporal motifs in time-dependent networks. J. Stat. Mech. Theory Exp. 2011, P11005 (2011).
Longa, A., Cencetti, G., Lepri, B. & Passerini, A. An efficient procedure for mining egocentric temporal motifs. Data Min. Knowl. Discov. 36, 355–378 (2022).
Galimberti, E., Barrat, A., Bonchi, F., Cattuto, C. & Gullo, F. Mining (maximal) span-cores from temporal networks. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management (Ed. ACM) 107–116 (ACM, 2018).
Ciaperoni, M. et al. Relevance of temporal cores for epidemic spread in temporal networks. Sci. Rep. 10, 12529 (2020).
Gauvin, L. et al. Randomized reference models for temporal networks. Preprint at https://arxiv.org/abs/1806.04032 (2018).
Gautreau, A., Barrat, A. & Barthélemy, M. Microdynamics in stationary complex networks. Proc. Natl Acad. Sci. U. S. A. 106, 8847–8852 (2009).
Salathé, M. et al. A high-resolution human contact network for infectious disease transmission. Proc. Natl Acad. Sci. U. S. A. 107, 22020–22025 (2010).
Barrat, A., Cattuto, C., Tozzi, A. E., Vanhems, P. & Voirin, N. Measuring contact patterns with wearable sensors: methods, data characteristics and applications to data-driven simulations of infectious diseases. Clin. Microbiol. Infect. 20, 10–16 (2014).
Masuda, N. & Holme, P. Detecting sequences of system states in temporal networks. Sci. Rep. 9, 795 (2019).
Gelardi, V., Le Bail, D., Barrat, A. & Claidiere, N. From temporal network data to the dynamics of social relationships. Proc. R. Soc. B 288, 20211164 (2021).
Valdano, E., Poletto, C. & Colizza, V. Infection propagator approach to compute epidemic thresholds on temporal networks: impact of immunity and of limited temporal resolution. Eur. Phys. J. B 88, 341 (2015).
Valdano, E., Ferreri, L., Poletto, C. & Colizza, V. Analytical computation of the epidemic threshold on temporal networks. Phys. Rev. X 5, 021005 (2015).
Clawson, W. et al. Computing hubs in the hippocampus and cortex. Sci. Adv. 5, eaax4843 (2019).
Clawson, W. et al. Disordered information processing dynamics in experimental epilepsy. Preprint at bioRxiv https://doi.org/10.1101/2021.02.11.430768 (2021).
Gelardi, V., Fagot, J., Barrat, A. & Claidière, N. Detecting social (in)stability in primates from their temporal co-presence network. Anim. Behav. 139, 239–254 (2019).
Hill, S. & Braha, D. Dynamic model of time-dependent complex networks. Phys. Rev. E 82, 046105 (2010).
Laurent, G., Saramäki, J. & Karsai, M. From calls to communities: a model for time-varying social networks. Eur. Phys. J. B 88, 301 (2015).
Markram, H., Gerstner, W. & Sjöström, P. J. Spike-timing-dependent plasticity: a comprehensive overview. Front. Synaptic Neurosci. 4, 2 (2012).
Singer, W. Neuronal synchrony: a versatile code for the definition of relations? Neuron 24, 49–65 (1999).
Varela, F., Lachaux, J.-P., Rodriguez, E. & Martinerie, J. The brainweb: phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2, 229–239 (2001).
Buzsáki, G. Neural syntax: cell assemblies, synapsembles, and readers. Neuron 68, 362–385 (2010).
Ikegaya, Y. et al. Synfire chains and cortical songs: temporal modules of cortical activity. Sci. (N.Y.) 304, 559–564 (2004).
Bonifazi, P. et al. GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science 326, 1419–1424 (2009).
Acknowledgements
N.P. has received funding from the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement no. 713750. Also, the project has been carried out with the financial support of the Regional Council of Provence-Alpes-Côte d’Azur and with the financial support of A*MIDEX (ANR-11-IDEX-0001-02), funded by the Investissements d’Avenir project funded by the French Government, managed by the French National Research Agency (ANR).
D.B. is supported by the European Union Innovative Training Network “i- CONN” (H2020 ITN 859937).
A.B. is supported by Agence Nationale de la Recherche (ANR) project DATAREDUX (ANR-19-CE46-0008).
Author information
Authors and Affiliations
Contributions
N.P., D.B. and A.B. designed the study and the experiment. N.P. developed the numerical tools, and produced the figures. N.P., D.B. and A.B. analysed the data and results and wrote and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests
Peer review
Peer review information
Nature Physics thanks Shi Zhou, Dan Braha and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary information
Supplementary Notes 1–5.
Rights and permissions
About this article
Cite this article
Pedreschi, N., Battaglia, D. & Barrat, A. The temporal rich club phenomenon. Nat. Phys. 18, 931–938 (2022). https://doi.org/10.1038/s41567-022-01634-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01634-8
This article is cited by
-
Attributed Stream Hypergraphs: temporal modeling of node-attributed high-order interactions
Applied Network Science (2023)