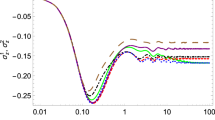
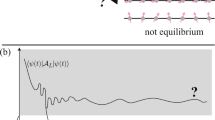
Abstract
Studies of the dynamics of open quantum systems are limited by the large Hilbert space of typical environments, which is too large to be treated exactly. In some cases, approximate descriptions of the system are possible, for example, when the environment has a short memory time or only interacts weakly with the system. Accurate numerical methods exist, but these are typically restricted to baths with Gaussian correlations, such as non-interacting bosons. Here we present a method for simulating open quantum systems with arbitrary environments that consist of a set of independent degrees of freedom. Our approach automatically reduces the large number of environmental degrees of freedom to those which are most relevant. Specifically, we show how the process tensor describing the effect of the environment can be iteratively constructed and compressed using matrix product state techniques. We demonstrate the power of this method by applying it to a range of open quantum systems, including bosonic, fermionic and spin environments. The versatility and efficiency of our automated compression of environments method provides a practical general-purpose tool for open quantum systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data presented in the figures including the parameter files to generate them are available online in the ‘examples’ subdirectory of the Zenodo repository at https://doi.org/10.5281/zenodo.5214128.
Code availability
The C++ computer code including documentation is available online at https://doi.org/10.5281/zenodo.5214128.
References
Breuer, H.-P. and Petruccione, F. The Theory of Open Quantum Systems (Oxford Univ. Press, 2002).
Plenio, M. B. & Huelga, S. F. Dephasing-assisted transport: quantum networks and biomolecules. New J. Phys. 10, 113019 (2008).
Rebentrost, P., Mohseni, M., Kassal, I., Lloyd, S. & Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 11, 033003 (2009).
Chin, A. W., Datta, A., Caruso, F., Huelga, S. F. & Plenio, M. B. Noise-assisted energy transfer in quantum networks and light-harvesting complexes. New J. Phys. 12, 065002 (2010).
Beige, A., Braun, D., Tregenna, B. & Knight, P. L. Quantum computing using dissipation to remain in a decoherence-free subspace. Phys. Rev. Lett. 85, 1762 (2000).
Verstraete, F., Wolf, M. M. & Cirac, J. I. Quantum computation and quantum-state engineering driven by dissipation. Nat. Phys. 5, 633–636 (2009).
de Vega, I. & Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 89, 015001 (2017).
Tanimura, Y. Stochastic Liouville, Langevin, Fokker–Planck, and master equation approaches to quantum dissipative systems. J. Phys. Soc. Jpn 75, 082001 (2006).
Plenio, M. B. & Knight, P. L. The quantum-jump approach to dissipative dynamics in quantum optics. Rev. Mod. Phys. 70, 101 (1998).
Redfield, A. G. The theory of relaxation processes. in Advances in Magnetic Resonance, Advances in Magnetic and Optical Resonance Vol. 1 (ed Waugh, J. S.) 1–32 (Academic Press, 1965).
Nazir, A. & McCutcheon, D. P. S. Modelling exciton–phonon interactions in optically driven quantum dots. J. Phys.: Condens. Matter 28, 103002 (2016).
Breuer, H.-P., Laine, E.-M., Piilo, J. & Vacchini, B. Colloquium: non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 88, 021002 (2016).
Tanimura, Y. & Kubo, R. Time evolution of a quantum system in contact with a nearly Gaussian-Markoffian noise bath. J. Phys. Soc. Jpn 58, 101–114 (1989).
Tanimura, Y. Numerically ‘exact’ approach to open quantum dynamics: the hierarchical equations of motion (HEOM). J. Chem. Phys. 153, 020901 (2020).
Prior, J., Chin, A. W., Huelga, S. F. & Plenio, M. B. Efficient simulation of strong system-environment interactions. Phys. Rev. Lett. 105, 050404 (2010).
Somoza, A. D., Marty, O., Lim, J., Huelga, S. F. & Plenio, M. B. Dissipation-assisted matrix product factorization. Phys. Rev. Lett. 123, 100502 (2019).
Nüßeler, A., Dhand, I., Huelga, S. F. & Plenio, M. B. Efficient simulation of open quantum systems coupled to a fermionic bath. Phys. Rev. B 101, 155134 (2020).
Feynman, R. & Vernon, F. The theory of a general quantum system interacting with a linear dissipative system. Ann. Phys. 24, 118 (1963).
Makri, N. & Makarov, D. E. Tensor propagator for iterative quantum time evolution of reduced density matrices. I. Theory. J. Chem. Phys. 102, 4600 (1995).
Makri, N. & Makarov, D. E. Tensor propagator for iterative quantum time evolution of reduced density matrices. II. Numerical methodology. J. Chem. Phys. 102, 4611 (1995).
Cygorek, M., Barth, A. M., Ungar, F., Vagov, A. & Axt, V. M. Nonlinear cavity feeding and unconventional photon statistics in solid-state cavity QED revealed by many-level real-time path-integral calculations. Phys. Rev. B 96, 201201 (2017).
Strathearn, A., Kirton, P., Kilda, D., Keeling, J. & Lovett, B. W. Efficient non-Markovian quantum dynamics using time-evolving matrix product operators. Nat. Commun. 9, 3322 (2018).
Cosacchi, M. et al. Path-integral approach for nonequilibrium multitime correlation functions of open quantum systems coupled to Markovian and non-Markovian environments. Phys. Rev. B 98, 125302 (2018).
Denning, E. V., Bundgaard-Nielsen, M. & Mørk, J. Optical signatures of electron-phonon decoupling due to strong light-matter interactions. Phys. Rev. B 102, 235303 (2020).
Cosacchi, M., Ungar, F., Cygorek, M., Vagov, A. & Axt, V. M. Emission-frequency separated high quality single-photon sources enabled by phonons. Phys. Rev. Lett. 123, 017403 (2019).
Seidelmann, T. et al. Phonon-induced enhancement of photon entanglement in quantum dot-cavity systems. Phys. Rev. Lett. 123, 137401 (2019).
Kaestle, O., Finsterhoelzl, R., Knorr, A. & Carmele, A. Continuous and time-discrete non-Markovian system-reservoir interactions: Dissipative coherent quantum feedback in Liouville space. Phys. Rev. Research 3, 023168 (2021).
Vagov, A., Croitoru, M. D., Glässl, M., Axt, V. M. & Kuhn, T. Real-time path integrals for quantum dots: quantum dissipative dynamics with superohmic environment coupling. Phys. Rev. B 83, 094303 (2011).
Quilter, J. H. et al. Phonon-assisted population inversion of a single InGaAs/GaAs quantum dot by pulsed laser excitation. Phys. Rev. Lett. 114, 137401 (2015).
Koong, Z. X. et al. Coherent dynamics in quantum emitters under dichromatic excitation. Phys. Rev. Lett. 126, 047403 (2021).
Palm, T. & Nalbach, P. Quasi-adiabatic path integral approach for quantum systems under the influence of multiple non-commuting fluctuations. J. Chem. Phys. 149, 214103 (2018).
Simine, L. & Segal, D. Path-integral simulations with fermionic and bosonic reservoirs: transport and dissipation in molecular electronic junctions. J. Chem. Phys. 138, 214111 (2013).
Rossi, F. & Kuhn, T. Theory of ultrafast phenomena in photoexcited semiconductors. Rev. Mod. Phys. 74, 895 (2002).
Hsieh, C.-Y. & Cao, J. A unified stochastic formulation of dissipative quantum dynamics. I. Generalized hierarchical equations. J. Chem. Phys. 148, 014103 (2018).
Hsieh, C.-Y. & Cao, J. A unified stochastic formulation of dissipative quantum dynamics. II. Beyond linear response of spin baths. J. Chem. Phys. 148, 014104 (2018).
Jørgensen, M. R. & Pollock, F. A. Exploiting the causal tensor network structure of quantum processes to efficiently simulate non-Markovian path integrals. Phys. Rev. Lett. 123, 240602 (2019).
Pollock, F. A., Rodríguez-Rosario, C., Frauenheim, T., Paternostro, M. & Modi, K. Non-Markovian quantum processes: complete framework and efficient characterization. Phys. Rev. A 97, 012127 (2018).
Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96 (2011).
Orús, R. A practical introduction to tensor networks: matrix product states and projected entangled pair states. Ann. Phys. 349, 117 (2014).
Luchnikov, I. A., Vintskevich, S. V., Ouerdane, H. & Filippov, S. N. Simulation complexity of open quantum dynamics: connection with tensor networks. Phys. Rev. Lett. 122, 160401 (2019).
Brandes, T. & Kramer, B. Spontaneous emission of phonons by coupled quantum dots. Phys. Rev. Lett. 83, 3021 (1999).
Barth, A. M., Vagov, A. & Axt, V. M. Path-integral description of combined Hamiltonian and non-Hamiltonian dynamics in quantum dissipative systems. Phys. Rev. B 94, 125439 (2016).
Nagy, D., Szirmai, G. & Domokos, P. Critical exponent of a quantum-noise-driven phase transition: the open-system Dicke model. Phys. Rev. A 84, 043637 (2011).
Mitchison, M. T. & Plenio, M. B. Non-additive dissipation in open quantum networks out of equilibrium. New J. Phys. 20, 033005 (2018).
Maguire, H., Iles-Smith, J. & Nazir, A. Environmental nonadditivity and Franck-Condon physics in nonequilibrium quantum systems. Phys. Rev. Lett. 123, 093601 (2019).
Gribben, D. et al. Exact dynamics of nonadditive environments in non-Markovian open quantum systems. PRX Quantum 3, 010321 (2022).
Krummheuer, B., Axt, V. M., Kuhn, T., D’Amico, I. & Rossi, F. Pure dephasing and phonon dynamics in GaAs- and GaN-based quantum dot structures: interplay between material parameters and geometry. Phys. Rev. B 71, 235329 (2005).
Roy-Choudhury, K. & Hughes, S. Spontaneous emission from a quantum dot in a structured photonic reservoir: phonon-mediated breakdown of Fermi’s golden rule. Optica 2, 434–437 (2015).
Hoeppe, U. et al. Direct observation of non-Markovian radiation dynamics in 3D bulk photonic crystals. Phys. Rev. Lett. 108, 043603 (2012).
Gangloff, D. A. et al. Quantum interface of an electron and a nuclear ensemble. Science 364, 62–66 (2019).
Scheuer, J. et al. Robust techniques for polarization and detection of nuclear spin ensembles. Phys. Rev. B 96, 174436 (2017).
Wang, H. & Thoss, M. Quantum dynamical simulation of electron-transfer reactions in an anharmonic environment. J. Phys. Chem. A 111, 10369 (2007).
Bramberger, M. & De Vega, I. Dephasing dynamics of an impurity coupled to an anharmonic environment. Phys. Rev. A 101, 012101 (2020).
Ye, E. & Chan, G. K.-L. Constructing tensor network influence functionals for general quantum dynamics. J. Chem. Phys. 155, 044104 (2021).
Bañuls, M. C., Hastings, M. B., Verstraete, F. & Cirac, J. I. Matrix product states for dynamical simulation of infinite chains. Phys. Rev. Lett. 102, 240603 (2009).
Acknowledgements
M. Cosacchi and V.M.A. are grateful for funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under project no. 419036043. A.V. acknowledges support from the Russian Science Foundation under Project 18-12-00429 and from the Basic Research Program at the HSE University. M. Cygorek and E.M.G. acknowledge funding from EPSRC grant no. EP/T01377X/1. B.W.L. and J.K. were supported by EPSRC grant no. EP/T014032/1.
Author information
Authors and Affiliations
Contributions
M. Cygorek, M. Cosacchi, A.V., and V.M.A. developed the concept of explicitly constructing the PT to simulate open quantum systems with arbitrary system–environment couplings. M. Cygorek, B.W.L., J.K. and E.M.G. contributed the idea of using MPO representations for efficient storage and evaluation of the PT. M. Cygorek is responsible for the details of the algorithm, implementation in the form of C++ code and generation of data. All the authors analysed and discussed the results and contributed to writing the Article.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–6.
Rights and permissions
About this article
Cite this article
Cygorek, M., Cosacchi, M., Vagov, A. et al. Simulation of open quantum systems by automated compression of arbitrary environments. Nat. Phys. 18, 662–668 (2022). https://doi.org/10.1038/s41567-022-01544-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01544-9
This article is cited by
-
Seeking a quantum advantage with trapped-ion quantum simulations of condensed-phase chemical dynamics
Nature Reviews Chemistry (2024)
-
Learning quantum systems
Nature Reviews Physics (2023)
-
Self-assembly for hybrid biomaterial of uridine monophosphate to enhance the optical phenomena
Chemical Papers (2023)