Abstract
MXenes are emerging layered materials that are promising for electrochemical energy storage and (opto-)electronic applications. A fundamental understanding of charge transport in MXenes is essential for such applications, but has remained under debate. While theoretical studies pointed to efficient band transport, device measurements have revealed thermally activated, hopping-type transport. Here we present a unifying picture of charge transport in two model MXenes by combining ultrafast terahertz and static electrical transport measurements to distinguish the short- and long-range transport characteristics. We find that band-like transport dominates short-range, intra-flake charge conduction in MXenes, whereas long-range, inter-flake transport occurs through thermally activated hopping, and limits charge percolation across the MXene flakes. Our analysis of the intra-flake charge carrier scattering rate shows that it is dominated by scattering from longitudinal optical phonons with a small coupling constant (α ≈ 1), for both semiconducting and metallic MXenes. This indicates the formation of large polarons in MXenes. Our work therefore provides insight into the polaronic nature of free charges in MXenes, and unveils intra- and inter-flake transport mechanisms in the MXene materials, which are relevant for both fundamental studies and applications.
Similar content being viewed by others
Main
Two-dimensional (2D) transition metal carbides and/or nitrides, known as MXenes, have attracted considerable attention as a consequence of their outstanding electronic, optical, mechanical and thermal properties1,2,3. The general formula of MXenes is Mn + 1XnTx (n = 1–4), where M represents the transition metal, X carbon and/or nitrogen and Tx the surface termination. A unique combination of tunable electronic properties (through the Mn + 1Xn backbone) and versatile surface chemistry (from Tx functionalization) results in many intriguing properties such as the metal-to-insulator transition, topological insulators and superconductivity4. As such, MXenes hold great promise for a variety of electronic and optoelectronic applications1,2,3.
In many applications, the electrical transport properties of MXenes are quintessential. Understanding the mechanism governing the electrical conductivity of MXenes is therefore important. Accordingly, many previous studies have investigated the conductivity of charge carriers, specifically as a function of temperature (T). However, controversial results, mainly between experiments and theoretical calculations, have been reported. Experimentally5,6,7,8, based on static electrical transport studies using four-probe methods, it has been shown that the conductivity σ increases at elevated temperature T (that is, dσ/dT > 0). This dependence was attributed to a thermally activated hopping transport. On the other hand, theoretical studies have predicted band-like transport9,10,11. For band transport, the charge carrier mobility typically increases with decreasing T (that is, dσ/dT < 0) as a result of the decreased carrier–phonon scattering probability at lower T. This contradiction between the theoretical and experimental results raises questions regarding the nature of the charge carriers and charge transport mechanism in MXenes. Owing to the polar nature of MXene crystals3, charge carriers can induce lattice distortions via Coulomb interactions. A quasi-particle, a so-called polaron, is normally introduced to describe the charge carriers dressed with lattice distortions. The carrier–phonon coupling constant α characterizes the strength of the coupling between charge carriers and phonons12. For sufficiently strong carrier–phonon coupling (α ≫ 6), self-trapped, localized polaron states, or so-called small polarons (with the lattice distortion limited to ~1 lattice unit), occur. Transport of small polarons requires thermal activation, which may explain the observed hopping-like transport behaviour in MXenes. For weaker coupling (α < 6), large polarons are formed; these are characterized by band-like transport of charge carriers with a renormalized effective mass. Large polaron mobility typically increases with decreasing temperature12,13. We note that other charge localization effects, for example, due to the presence of a high density of defects (depending on the quality of the samples), could lead to hopping-like transport as well14. Given the increasing interest in MXenes for electrical and electrochemical applications, it is crucial to understand the nature of charge species and their transport mechanism across materials and interfaces.
In this Article, we present a unifying picture of charge transport in liquid-exfoliated MXenes, using semiconductor-like Nb4C3Tx and metallic Ti3C2Tx as model systems. By comprehensively employing ultrafast terahertz and static electrical transport measurements, we distinguish the short- and long-range transport characteristics of MXene films. We reveal that while band-like transport dominates intra-flake charge conduction in MXenes, inter-flake transport occurs via thermally activated hopping processes and becomes the limiting step for charge percolation across the MXene flakes (see the illustration in Fig. 1a). More importantly, by analysing contributions from impurities, acoustic and longitudinal optical (LO) phonons to the charge scattering mechanisms, we further show that carrier–LO phonon scattering dominates the carrier transport at room T, with a small carrier–LO phonon coupling constant (α ≈ 1). The small α indicates the formation of large polarons in the materials (see the illustration in Fig. 1b). These results suggest that, for both semiconducting and metallic MXenes, large polaron formation is a generic property that fundamentally affects the intrinsic charge transport and carrier lifetime. Our results reconcile the debate between previous theoretical and experimental studies and shed light on the charge species and their transport mechanisms in MXenes.
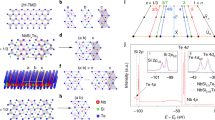
a, Schematic of charge transport within the network of MXene flakes. The inter-crystallite charge carrier hopping (indicated by the dashed arrows) is revealed as the charge transport bottleneck, limiting the overall charge conduction between electrodes. b, Scheme for ultrafast OPTP experiments to characterize the intra-MXene flake transport of charge carriers. Inset: the formation of a large polaron, in which a conduction electron is dressed by lattice deformations extending over several lattice constants. c, XRD spectra of Nb4AlC3 MAX (the mother compounds) and resultant Nb4C3Tx after etching. Inset: the crystal structure of Nb4C3Tx MXene. d, Raman spectrum of delaminated Nb4C3Tx MXene. e, TEM image of Nb4C3Tx MXene. Inset: corresponding SAED pattern, which shows the high crystallinity and hexagonal symmetry of the crystal lattice.
Results and discussion
We present detailed structural characterizations for Nb4C3Tx MXene in Fig. 1, and show those for the well-established Ti3C2Tx MXene in Supplementary Fig. 1. Figure 1c presents the X-ray diffraction (XRD) pattern of the Nb4AlC3 MAX precursor and the resultant Nb4C3Tx MXene following the selective etching of aluminium element by hydrogen fluoride. After etching, the diffraction peaks corresponding to the MAX phase either disappear or greatly diminish in intensity, along with the appearance of a new peak at a 2θ of ~5°. This new peak can be assigned to the (002) facet for Nb4C3Tx MXene6. Furthermore, Raman spectroscopy displays two pronounced peaks at ~240 cm−1 and 675 cm−1, corresponding to Nb–O and Nb–C vibrational modes, respectively (Fig. 1d). The emergence of the Nb–O peak at ~240 cm−1 points to (partial) surface oxidation, which is unavoidable during the synthesis process. Such surface oxidation might partially contribute to the semiconducting nature of Nb4C3Tx MXene in our study. In other MXenes (for example, Ti4N3Tx), surface oxidation has been reported to lead to a bandgap opening, thus provoking a metal-to-semiconductor transition15. In addition, as shown in X-ray photoelectron spectroscopy (XPS) results, the as-synthesized Nb4C3Tx has mixed termination (Supplementary Fig. 2 and Supplementary Discussion). High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) and energy-dispersive X‐ray analysis (EDX) display uniform distributions of Nb, C, F and O in Nb4C3Tx MXene (Supplementary Fig. 3). A selected-area electron diffraction (SAED) pattern of a Nb4C3Tx flake demonstrates the high crystallinity and hexagonal symmetry (P63/mmc), in line with typical MXene structures3,6. We further conducted high-resolution atomic force microscope (AFM) measurements, which are described in Supplementary Fig. 4. Based on the analysis, over ~60% of the MXene flakes are ~5 nm in thickness, corresponding to a bilayer structure for Nb4C3Tx MXene6. The homogeneity and good quality of our samples are further confirmed by transmission electron microscopy (TEM) and scanning electron microscopy characterizations in Fig. 1e and Supplementary Fig. 5, showing that the lateral dimension is on the order of several micrometres.
Niobium-based MXene has been predicted to have a narrow bandgap (on the order of ~0.1 eV)16. In line with this prediction, the bandgap of Nb4C3Tx in our study was determined to be ~0.19 eV from the Tauc plot method (Supplementary Fig. 7). Static terahertz measurements further support the narrow-gap nature of the Nb4C3Tx MXene. We find negligible conductivity (or, equivalently, absorption) by free charge carriers in our 0–2 THz window (corresponding to 0–8 meV; Fig. 2a). In contrast, the metallic Ti3C2Tx exhibits substantial conductivity (absorption) in this terahertz region (Fig. 2a).
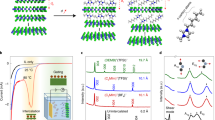
a, Static terahertz conductivity of Nb4C3Tx and Ti3C2Tx MXene thin films. b,c, The fluence-dependent, time-resolved photoconductivity of semiconducting Nb4C3Tx (b) and metallic Ti3C2Tx (c) MXenes thin films, following 1.55 eV photoexcitation at room temperature.
The different—semiconducting and metallic—natures of Nb4C3Tx and Ti3C2Tx MXenes, respectively, give rise to distinct photoresponses, as shown in Fig. 2b,c. Photoexcitation of a semiconductor like Nb4C3Tx promotes electrons to the conduction band, increasing the material’s conductivity from ~0 (Fig. 2a) to a finite value (that is, giving rise to a positive photoconductivity)17. In contrast, for metallic materials such as Ti3C2Tx, optical excitation of conducting electrons results in heating up of the electron gas, which gives rise to a transiently reduced conductivity (that is, negative photoconductivity)18. The samples’ photoconductivity is determined by optical-pump terahertz-probe (OPTP) spectroscopy. OPTP spectroscopy provides insight into the electrical transport properties of charge carriers in a contact-free and non-invasive fashion17,19,20,21. Thanks to the transient nature of terahertz probe pulses (with duration of ~1 ps), terahertz spectroscopy characterizes short-range, intra-flake transport (over approximately tens of nanometres) in MXenes17,22. By monitoring the photo-induced terahertz absorption (ΔE) at various pump–probe delays, the photoconductivity (Δσopt) dynamics can be quantified using the thin-film approximation as follows17:
where Z0 = 377 Ω is the impedance of free space, nsub = 1.95 is the refractive index of the fused-silica substrate in the terahertz range and L is the excitation thickness. Epump and E0 represent the transmitted terahertz electric field with and without photoexcitation, respectively (see Methods for details).
The photoconductivity of Nb4C3Tx MXene (Fig. 2b) decays swiftly within several picoseconds, followed by a slow decay (>1 ns, limited by our temporal probe window). We attribute the fast photoconductivity decay in the Nb4C3Tx MXene to the trapping of free charge carriers at defects. This claim is supported by the fluence-dependent OPTP dynamics analysis, in which trap filling is observed (Supplementary Fig. 8 and Supplementary Discussion)23. In addition, by comparing different sample batches, we observe that, for samples with a slightly higher degree of oxidation (characterized by Raman spectroscopy), the relative weight of the fast decay is higher (Supplementary Fig. 9). As such, surface oxidation is a potential candidate for defect formation and charge carrier trapping15. The negative photoconductivity in Ti3C2Tx MXene confirms the metallic nature of Ti3C2Tx. The transient photoconductivity decrease in metallic Ti3C2Tx MXene is consistent with previous reports24. Therefore, the ultrafast terahertz photoconductivity traces shown in Fig. 2 confirm the semiconductor-like behaviour in Nb4C3Tx MXene and a metallic response in Ti3C2Tx MXene.
To investigate the charge transport mechanism in Nb4C3Tx MXenes, we complementarily employed temperature-dependent ultrafast OPTP and static electrical measurements. To provide a fair comparison between terahertz and electrical studies, we followed the same film deposition recipe to make thin films of Nb4C3Tx. As shown in Fig. 3a, the photoconductivity increases at reduced temperatures by a factor of 3–4, that is, dΔσopt/dT < 0. Meanwhile, a substantial, yet opposite trend (dσele/dT > 0) is observed in electrically measured conductivity. The spectroscopic result suggests that band-like transport dominates the charge transport mechanism in Nb4C3Tx MXene, with thermally populated phonons limiting the charge mobility through carrier–phonon scattering. Notably, a temperature dependence T−β of the conductivity has been predicted in molybdenum- and titanium-based MXenes, with 1.5 < β < 2.1 (refs. 9,10). Our results reveal β ≈ 1 for the averaged long-lived photoconductivity (as shown in Fig. 3b). This experimentally observed weaker temperature dependence of the conductivity suggests that, besides the dominant role of phonons, impurity scattering may also contribute to the limitation of the charge transport in Nb4C3Tx MXene.
a, The time-resolved terahertz photoconductivity dynamics, at temperatures ranging from 78 K to 404 K under vacuum conditions (pressure of <1.8 × 10−4 mbar). The studies are conducted using excitations of 1.55 eV photons at an absorbed fluence of ∼3.1 × 1018 m−2. Data are shifted horizontally by 1 ps for clarity. b, A direct comparison of T-dependent charge carrier conductivity determined optically by terahertz spectroscopy (by taking the averaged photoconductivity from 600 ps to 800 ps following excitations) and electrically via the van der Pauw four-probe method. The red line through the photoconductivity data shows a T−1 dependence. Error bars represent the standard error of the mean.
We note that the dΔσopt/dT < 0 in our spectroscopic result is in line with previous theoretical studies9,10,11, but in stark contrast to the dσele/dT > 0 in device results shown here and also reported previously for other MXene materials measured using the four-probe method5,6,7. This apparent contradiction can be explained as follows. In the terahertz photoconductivity measurements, the transient, picosecond-duration terahertz field drives the charge carrier over approximately tens of nanometres. Therefore, terahertz spectroscopy provides the local, intra-flake charge transport information (given the micrometre size of the flakes). Meanwhile, static electrical transport studies provide long-range charge carrier conductance over macroscopic distances between the electrodes under d.c. bias14,25. As such, we can rationalize the results by postulating band-like transport dominating intra-flake charge conduction, while the inter-flake hopping is the rate-limiting step for charge percolation through devices consisting of many MXene flakes. Importantly, such a scenario reconciles the debate between previous theoretical and experimental studies on the charge transport mechanism in MXenes. Moreover, these findings are relevant for the optimization of MXene-based devices: for example, interface molecular engineering to enhance the inter-flake transport or increasing the geometrical size is therefore recommended26.
To further confirm and investigate the band-like, intra-flake charge transport in MXenes, we disentangled the contribution of charge mobility (μ) from carrier density (ΔN) to the photoconductivity Δσopt (= ΔNeμ, where e is the elementary charge) by measuring the temperature-dependent photoconductivity spectra employing terahertz time-domain spectroscopies (THz-TDS; for details of the measurement and data analysis, see Methods). We recorded the conductivity spectra at a delay of ~200 ps after photoexcitation to ensure a quasi-steady-state charge carrier situation. The frequency-resolved complex photoconductivity spectra are shown in Fig. 4a. We analysed the spectra using the Drude–Smith (DS) model and found that the model describes the data well. The DS model describes the transport behaviour of free carriers in a medium, where charges experience a preferentially backscattering effect due to nanoscale confinements (the presence of grain boundaries, for example)17,27,28. The DS model equation reads
where τ, ωp, ε0 and m* are the effective carrier momentum scattering time, plasma frequency, vacuum permittivity and charge effective mass, respectively. The parameter c characterizes the probability that the charges backscatter between the scattering events, with the values ranging from 0 (isotropic scattering) to −1 (completely backscattering). The best fit to the DS model yields the parameters of τ, ωp and c, which are plotted as a function of temperature (Fig. 4b and Supplementary Fig. 10). Interestingly, we find that ωp and c depend very weakly on temperature, whereas τ increases drastically with lowering temperatures, from 38 ± 6 fs at 404 K to 95 ± 3 fs at 78 K. This substantial change demonstrates the dominant role of scattering time τ and thus effective charge mobility µ \((={\frac{{e \, \tau }}{{m^\ast }}}{\left( {1 + c} \right)})\) (refs. 17,27) in the d.c. limit in governing the photoconductivity amplitude as shown in Fig. 2. The threefold increase in scattering time is quantitatively consistent with the approximately three- to fourfold increase in photoconductivity amplitude. Based on these parameters, the intra-flake charge carrier mobility in Nb4C3Tx can readily reach ~103 cm2 V−1 s−1 at room temperature, using a reduced effective carrier mass of 0.04m0 (ref. 16).
a, Complex photoconductivity for the semiconductor-like Nb4C3Tx thin film, measured at ~200 ps after photoexcitation at varying temperatures. b, Scattering times τ of Nb4C3Tx as a function of temperature. c, T-dependent scattering rate of Nb4C3Tx. d, Complex static terahertz conductivity (σopt) for metallic Ti3C2Tx thin films at varying temperatures. e, T-dependent scattering time of Ti3C2Tx. Inset: \({\omega _{\rm{p}}^2}\) at various T. The dashed lines serve as a guide to the eye. f, T-dependent scattering rate of Ti3C2Tx. In a and d, the real and imaginary parts of conductivity are shown in red and blue, respectively, and the solid lines represent the fits to the DS model explained in the main text. In c and f, the solid lines are results of a transport model that includes the acoustic phonon (black dashed line), the LO phonon (blue dashed line) and impurity scattering (orange dashed line), as described in the main text. The error bars in b, c, e and f are the standard deviations calculated from the fits. Triangles represent the carrier–acoustic phonon scattering rates obtained from the DFT calculations described in the text.
To quantitatively analyse the T-dependent scattering mechanism, we consider charge scattering contributions from both phonons and impurities following Matthiessen’s Law (for an extended discussion see Methods)25:
where γ is the total scattering rate, and γac, γLO and γimp are the scattering rates due to acoustic phonons, LO phonons and impurities, respectively.
Under the effective mass approximation, the acoustic phonon scattering rate reads29
where kB, cii and Edef represent the Boltzmann constant, the elastic constant and the electron deformation potential, respectively (see Methods for more details).
The term γLO(T) describes the scattering from LO phonons following30
where ωLO, mp and α are the angular frequency of the LO phonon, the polaron effective mass and the carrier–LO phonon coupling constant, respectively. This expression is valid in the limit of weak electron–LO phonon coupling (α < 6, justified below). f(α) is a dimensionless function, slowly varying from 1.0 to 1.2 for sufficiently small coupling constant (0 < α < 4)30. Here we use ωLO = 19.5 THz, estimated from other MXene systems9,31,32. This ~20-THz LO phonon mode is associated with the in-plane vibration in the carbon-based MXene structures, which is theoretically predicted to dominate the carrier–LO phonon interaction over all other phonon modes9,33. The calculated phonon linewidth (which is positively correlated with the electron–phonon coupling strength) for ωLO (= 19.5 THz) is several times higher than those for other optical phonon branches.
In contrast to the phonon-scattering mechanism, defect scattering, for example, from ionic impurities, increases as the temperature decreases. The typical temperature dependence for ionic impurity scattering rate scales as25
where A is a prefactor characterizing the strength of impurity scattering.
Following the above model (equations (3)–(6)), we reproduce the temperature dependence of the effective scattering rate (defined by \({\gamma} = {\frac{1}{\tau }}\)) using only two adjustable parameters (A and α) (for details see Methods). As shown in Fig. 4c, the LO-phonon scattering dominates the charge transport over the entire temperature range, while impurity scattering becomes notable only at lower temperatures (T < 150 K). Acoustic phonon scattering is not required to describe the data. This is in line with both density functional theory (DFT) calculations, which show γac(T) < 1 THz (see below and Supplementary Fig. 15), and previous theoretical predictions9. The analysis yields the value of α to be 0.77 ± 0.10. The small value of α (<6) indicates the formation of large polarons in Nb4C3Tx thin films.
The large polaron limit is further confirmed by the more general Feynman polaron theory. This theory is non-perturbative and applicable for arbitrary coupling strength34,35,36. By variationally solving the Feynman polaron model36, the data analysis provides the carrier–LO phonon coupling constant in the range of 0.5 < α < 4 for Nb4C3Tx (Supplementary Fig. 14a and Supplementary Discussion).
An independent estimate of the electron–phonon coupling strength can be obtained from the Landau–Pekar model (equation (7)), which is widely employed to estimate the charge–LO phonon coupling strengths12,13,36. Strictly speaking, the model possesses an intrinsic limitation, as it is designed to treat continuum Fröhlich polarons, but formally justified results can only be obtained in the strong electron–phonon coupling regime13,34,37,38:
where εopt and εs are, respectively, the optical and static dielectric constants, and ħ is the reduced Planck constant. The dielectric function for Nb4C3Tx MXene versus the photon energy in the infrared to ultraviolet (IR–UV) range (0.4–3.1 eV) is shown in Supplementary Fig. 11. In the measured range, our spectra are very similar to the theoretical results of that in Ti3C2Tx MXene39. Therefore, considering equation (7) as well as the dielectric properties (εopt ≈ 4–6 from our measurement, εs = 22 based on the theoretical study), we infer 0.74 < α < 1.29. This quantitative agreement between α obtained from the experiment and that obtained from the Fröhlich polaron theory supports the occurrence of large polaron transport in Nb4C3Tx MXene materials.
Additional evidence for the dominating role of optical phonons in limiting the electrical transport properties of MXenes is provided by first-principles DFT calculations (for details see Methods). In short, we have performed numerical simulations of the full Boltzmann transport equation on Nb4C3, Nb4C3Tx (with Tx = O2 and (OH)2), Ti3C2 and Ti3C2Tx (with Tx = (OH)2), using a constant relaxation time for acoustic phonons that is calculated ab initio in the deformation potential approximation. The calculated scattering rates vary with both the nature of the metal ion (being systematically smaller for Ti than for Nb) and of the functional groups (with a reduction when oxygenated species are present), but are consistently below 1 THz for all cases in the T range considered (Supplementary Fig. 15). This supports our claim of the minor role of acoustic phonon scattering in determining the electrical conductivity in MXenes. Furthermore, if we apply the same formalism but using the measured scattering rates (thus accounting for optical phonons), the charge mobility values at room temperature decrease from ~104 cm2 V−1 s−1 in the acoustic limit down to ~103 cm2 V−1 s−1, in good agreement with the experimental data (Supplementary Fig. 16).
Given the very similar dielectric constants for different types of MXene structure39, we expect that the formation of large polarons in MXenes is universal. To validate such a statement, we further studied the charge transport mechanism in metallic Ti3C2Tx—the model MXene widely used for electrochemical energy storage applications1,2,3. The metallic nature of Ti3C2Tx MXene allows us to evaluate its complex conductivity by performing static THz-TDS measurements without involving optical excitations. In static THz-TDS measurements, we compared the amplitude and phase of the terahertz pulses transmitted through the substrate alone and the sample on the substrate in the frequency domain17,22. We conducted T-dependent static THz-TDS measurement from 78 to 397 K (Fig. 4d). Analysing the complex terahertz conductivity with the DS model yields scattering time τ, plasma frequency ωp and backscattering rate c, at various T. As shown in Fig. 4e, at elevated temperatures, scattering by phonons limits the scattering time, revealing a band-like charge transport nature. Interestingly, with rising T, the \({\omega _{\rm{p}}^2}\) (∝ carrier density) increases, probably due to the de-trapping of charge carriers by thermal activation (Fig. 4e, inset). The excess carrier density in the high-T regime (>288 K) could impose the additional carrier–carrier interaction channel onto the scattering mechanism. This is also supported by the T-dependent backscattering rate c, where c remains constant from 78 to 269 K, but increases in absolute magnitude when T exceeds 288 K (Supplementary Fig. 12). As such, to prevent the contribution from carrier–carrier scattering, we limited our analysis of the scattering rate in Ti3C2Tx MXene to T ranging from 78 to 269 K. Following Matthiessen’s rule and the model discussed for Nb4C3Tx, we find that the T-dependent scattering rate can be described properly by considering the scattering from phonons and impurity (for details see the Methods). As shown in Fig. 4f, the carrier–LO phonon scattering dominates the overall scattering rate in the high-T regime (>100 K), whereas the impurity scattering governs in the low-T range. Notably, the analysis yields carrier–LO phonon coupling α of 0.50 ± 0.05, indicating the formation of large polarons also in Ti3C2Tx MXene. Independently, we further calculated α following the Landau–Pekar polaron model (equation (7)) to be between 0.44 and 1.04, and, by solving the Feynman polaron model (Supplementary Fig. 14b), we obtained the carrier–LO phonon coupling constant in the range of 0.5 < α < 3 for Ti3C2Tx. Interestingly, the inferred carrier-impurity scattering rates in both Ti3C2Tx and Nb4C3Tx MXenes are very similar (Supplementary Fig. 13). We observed variations in trapping due to varying defect densities in different samples, yet the charge scattering time in Nb4C3Tx is independent of the defect level (Supplementary Fig. 9). These results suggest that charge carriers might be protected as large polarons, leading to the reduced charge scattering, despite the unavoidable high defect density in MXenes40,41. We note that angle-resolved photoemission spectroscopy (ARPES) is instructive for identifying the presence of polaronic features42,43. A recent ARPES study has provided the evidence of polaron states in single crystals of the parent phase of MXene, MAX compounds, consistent with our claim of polaron formation in MXenes44.
Considering Fröhlich polaron theory and the similar dielectric constants for different types of MXene structure, weak carrier–LO phonon coupling is probably a generic property of MXenes, leading to large polaron formation. Experimentally, we indicate the presence of large polarons in two popular MXenes, including semiconducting Nb4C3Tx and metallic Ti3C2Tx MXenes. Large polaron formation may determine not only the intrinsic charge transport, but also carrier lifetimes in MXenes. For example, in organic–inorganic perovskites, the formation of large polarons has been proposed to effectively screen the defect potential, resulting in mobile charge carriers with high defect tolerance40. The indication of large polaron formation in MXenes may partially rationalize the reported extremely high carrier mobility in this class of 2D materials, despite structural and surface defects.
Conclusions
In this Article, we reconcile the debate between previous theoretical and experimental studies on the charge transport mechanism and propose a unifying picture of charge transport in MXenes. This is achieved by combining terahertz and static electrical transport measurements to distinguish the short- and long-range transport characteristics. We reveal that the band-like charge transport governs intra-flake charge transport in MXenes, whereas inter-flake transport occurs by hopping and becomes the limiting step for charge percolation through the network of MXene flakes. Furthermore, by analysing the charge carrier scattering following Matthiessen’s law, we find that carrier–LO phonon scattering dominates the intra-flake carrier transport for both semiconducting and metallic MXenes. The resultant small carrier–LO coupling constant (α ≈ 1) indicates large polaron formation in MXenes. Our work sheds light on the polaronic nature of free charges in MXenes, and unveils intra- and inter-flake transport mechanisms in the MXene network, relevant for both fundamental studies and applications.
Methods
Material preparation
Nb4C3Tx MXene was synthesized according to the previously reported hydrogen fluoride etching method45. Briefly, 0.8 g of Nb4AlC3 MAX was etched by 20 ml of 49 wt% hydrogen fluoride aqueous solution at room temperature for 96 h. After washing by deionized water until the pH was above 6.0, the obtained multilayer Nb4C3Tx was further delaminated by tetramethylammonium hydroxide (TMAOH; 25% in H2O) with magnetic stirring for 5 h. The Nb4C3Tx MXene nanosheets were obtained by repeatedly washing and sonication in deionized water for 1 h. The sediment without delamination was removed by centrifugation at 2,000 r.p.m. for 20 min and the delaminated MXene flakes in supernatant were collected for subsequent measurements.
Material characterizations
The morphology of each sample was characterized via scanning electron microscopy (Zeiss Gemini S4 500) and TEM (FEI Talos F200X, 200 kV). Chemical compositions of the samples were analysed by XRD using a PW1820 X-ray diffractometer with Cu Kα radiation. Raman spectra were measured on a Renishaw inVia reflex spectrometer with a laser excitation of 532 nm. XPS spectra were recorded with a a Kratos Axis UltraDLD spectrometer using the monochromatic Al Kα source (1,486.6 eV). The static electrical conductivities were measured using the van der Pauw four-probe method, based on a commercial Lakeshore Hall system (9700A).
Terahertz spectroscopy set-up
The terahertz spectroscopy was powered by a femtosecond laser source providing pulses with a duration of ~50 fs and a repeating frequency of 1 kHz, at a central wavelength of 800 nm. The terahertz radiation was generated by the optical rectification effect in a ZnTe nonlinear crystal (along 〈110〉 orientation), and the terahertz probe field was mapped out through electro-optical sampling by femtosecond laser pulses in a second ZnTe detection crystal. For optical-pump terahertz probe measurements, the terahertz absorption induced by optical excitations (here, 800 nm) was monitored by fixing the sampling beam to the peak of the terahertz field. In this configuration, we measured time-dependent pump-induced terahertz absorption by tuning the time delay between the pump and terahertz probe. The entire terahertz set-up was kept under nitrogen purging to avoid terahertz absorption by vapours. The samples were either purged by dry N2 or placed under vacuum conditions (<2 × 10−4 mbar) during measurements.
Modelling the charge scattering rate in MXenes
The charge scattering contributions were analysed following Matthiessen’s law, by considering the carrier interaction with acoustic phonons, LO phonons and impurities (equation (3)). We considered the carrier–acoustic phonon scattering under the effective mass approximation (equation (4))29, and we took the elastic constant cii = 3.86 × 1012 dyn cm−2 from Nb4C3Tx MXene in the literature6. The electron deformation potential, Edef, defined as the linear displacement coefficient of the single electron band energy, was used to characterize the electron–acoustic phonon coupling strength. Neither m* nor Edef has been reported previously in Nb4C3Tx MXene materials. Considering the similarity of the chemical structures of Nb4C3Tx and Nb2CTx MXenes, we estimated the values of m* and Edef from those in Nb2CTx MXene16,46. The modification of the lower oxidation state in the inner transition metal atoms to m* and Edef is expected to be small47,48,49. For carrier–LO phonon scattering rate γLO(T) (equation (5)), in the moderate coupling regime (α < 6) we took into account the polaron mass mp and the effective charge mass m* by \({\frac{{m_{\rm{p}}}}{{m^\ast }}} = {\left( {{1} + {\frac{\alpha }{6}} + {\frac{{\alpha ^2}}{{40}}} + {\cdots }}\right)}\) (ref. 30). As for carrier-impurity scattering (equation (6)), we primarily considered the contribution from ionic impurity scattering, where the scattering increases as the temperature decreases. For modelling the scattering rate in Ti3C2Tx MXene, we applied the same method and took the values of cii, m* and Edef from the literature46,50,51.
Computational details
DFT calculations were performed with the projector-augmented wave (PAW) basis set, as implemented in the VASP code52,53, with the exchange and correlation effects treated at the Perdew−Burke−Ernzerhof (PBE) level54. Dispersion forces by Grimme correction (PBE+D2)55 and dipole moment correction along the c axis (z direction and perpendicular to the MXene surface) were incorporated with a kinetic energy cutoff of 500 eV and using a Monkhorst–Pack sampling of 3 × 3 × 1 for the Brillouin zone integration for all geometry optimizations. Vacuum spacing was set to be 30 Å to avoid the interaction with periodic images. Subsequent self-consistent field calculations were performed using a dense K-point grid of 100 × 100 × 1 for the Brillouin zone integration. Electron conductivities and mobilities were estimated using the semi-classical Boltzmann transport theory within both the deformation potential approach and the relaxation time approximations56,57,58.
Data availability
All data generated or analysed in this study are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
Code availability
The code used to analyse the data and perform numerical simulations is available from the corresponding authors upon reasonable request.
References
VahidMohammadi, A., Rosen, J. & Gogotsi, Y. The world of two-dimensional carbides and nitrides (MXenes). Science 372, eabf1581 (2021).
Jiang, X. et al. Two-dimensional MXenes: from morphological to optical, electric and magnetic properties and applications. Phys. Rep. 848, 1–58 (2020).
Hantanasirisakul, K. & Gogotsi, Y. Electronic and optical properties of 2D transition metal carbides and nitrides (MXenes). Adv. Mater. 30, 1804779 (2018).
Kamysbayev, V. et al. Covalent surface modifications and superconductivity of two-dimensional metal carbide MXenes. Science 369, 979–983 (2020).
Han, M. et al. Tailoring electronic and optical properties of MXenes through forming solid solutions. J. Am. Chem. Soc. 142, 19110–19118 (2020).
Lipatov, A. et al. Electrical and elastic properties of individual single-layer Nb4C3Tx MXene flakes. Adv. Electron. Mater. 6, 1901382 (2020).
Halim, J. et al. Variable range hopping and thermally activated transport in molybdenum-based MXenes. Phys. Rev. B 98, 104202 (2018).
Hart, J. L. et al. Control of MXenes’ electronic properties through termination and intercalation. Nat. Commun. 10, 522 (2019).
Jing, Z. et al. Electron–phonon scattering limited intrinsic electrical conductivity of MXenes X2C (X = Ti or Mo). J. Phys. D 54, 015301 (2021).
Xu, M., Yang, J. & Liu, L. Temperaÿture-dependent optical and electrical properties of bulk Ti2AlC and two-dimensional MXenes from first-principles. Physica B 560, 146–154 (2019).
Zhang, X., Zhao, X., Wu, D., Jing, Y. & Zhou, Z. High and anisotropic carrier mobility in experimentally possible Ti2CO2 (MXene) monolayers and nanoribbons. Nanoscale 7, 16020–16025 (2015).
Alexandrov, A. S. & Devreese, J. T. Advances in Polaron Physics (Springer, 2010).
Franchini, C., Reticcioli, M., Setvin, M. & Diebold, U. Polarons in materials. Nat. Rev. Mater. 6, 560–586 (2021).
Mei, Y. et al. Crossover from band-like to thermally activated charge transport in organic transistors due to strain-induced traps. Proc. Natl Acad. Sci. USA 114, 6739–6748 (2017).
Djire, A., Zhang, H., Liu, J., Miller, E. M. & Neale, N. R. Electrocatalytic and optoelectronic characteristics of the two-dimensional titanium nitride Ti4N3Tx MXene. ACS Appl. Mater. Interfaces 11, 11812–11823 (2019).
Shao, Y., Zhang, F., Shi, X. & Pan, H. N-functionalized MXenes: ultrahigh carrier mobility and multifunctional properties. Phys. Chem. Chem. Phys. 19, 28710–28717 (2017).
Ulbricht, R., Hendry, E., Shan, J., Heinz, T. F. & Bonn, M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Rev. Mod. Phys. 83, 543–586 (2011).
Tielrooij, K. J. et al. Photoexcitation cascade and multiple hot-carrier generation in graphene. Nat. Phys. 9, 248–252 (2013).
Fu, S. et al. Long-lived charge separation following pump-wavelength-dependent ultrafast charge transfer in graphene/WS2 heterostructures. Sci. Adv. 7, eabd9061 (2021).
Zheng, W., Bonn, M. & Wang, H. I. Photoconductivity multiplication in semiconducting few-layers MoTe2. Nano Lett. 20, 5807–5813 (2020).
Shan, J., Wang, F., Knoesel, E., Bonn, M. & Heinz, T. F. Measurement of the frequency-dependent conductivity in sapphire. Phys. Rev. Lett. 90, 247401 (2003).
Němec, H., Kužel, P. & Sundström, V. Charge transport in nanostructured materials for solar energy conversion studied by time-resolved terahertz spectroscopy. J. Photochem. Photobiol. A 215, 123–139 (2010).
Ballabio, M., Fuertes Marron, D., Barreau, N., Bonn, M. & Canovas, E. Composition-dependent passivation efficiency at the CdS/CuIn1-xGaxSe2 interface. Adv. Mater. 32, 1907763 (2020).
Li, G. et al. Dynamÿical control over terahertz electromagnetic interference shielding with 2D Ti3C2Ty MXene by ultrafast optical pulses. Nano Lett. 20, 636–643 (2020).
Jacoboni, C. Theory of Electron Transport in Semiconductors (Springer, 2010).
Ippolito, S. et al. Covalently interconnected transition metal dichalcogenide networks via defect engineering for high-performance electronic devices. Nat. Nanotechnol. 16, 592–598 (2021).
Cocker, T. L. et al. Microscopic origin of the Drude-Smith model. Phys. Rev. B 96, 205439 (2017).
Li, G., Natu, V., Shi, T., Barsoum, M. W. & Titova, L. V. Two-dimensional MXenes Mo2Ti2C3Tz and Mo2TiC2Tz: microscopic conductivity and dynamics of photoexcited carriers. ACS Appl. Energy Mater. 3, 1530–1539 (2020).
Bardeen, J. & Shockley, W. Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 80, 72–80 (1950).
Low, F. E. & Pines, D. Mobility of slow electrons in polar crystals. Phys. Rev. 98, 414–418 (1955).
Bafekry, A., Akgenc, B., Ghergherehchi, M. & Peeters, F. M. Strain and electric field tuning of semi-metallic character WCrCO2 MXenes with dual narrow band gap. J. Phys. Condens. Matter 32, 355504 (2020).
Luo, Y., Cheng, C., Chen, H. J., Liu, K. & Zhou, X. L. Systematic investigations of the electron, phonon and elastic properties of monolayer M2C (M = V, Nb, Ta) by first-principles calculations. J. Phys. Condens. Matter 31, 405703 (2019).
Hu, T. et al. Vibrational properties of Ti3C2 and Ti3C2T2 (T = O, F, OH) monosheets by first-principles calculations: a comparative study. Phys. Chem. Chem. Phys. 17, 9997–10003 (2015).
Feynman, R. P., Hellwarth, R. W., Iddings, C. K. & Platzman, P. M. Mobility of slow electrons in a polar crystal. Phys. Rev. 127, 1004–1017 (1962).
Hendry, E., Wang, F., Shan, J., Heinz, T. F. & Bonn, M. Electron transport in TiO2 probed by THz time-domain spectroscopy. Phys. Rev. B 69, 081101 (2004).
Frost, J. M. Calculating polaron mobility in halide perovskites. Phys. Rev. B 96, 195202 (2017).
Sio, W. H., Verdi, C., Poncé, S. & Giustino, F. Ab initio theory of polarons: formalism and applications. Phys. Rev. B 99, 235139 (2019).
Sio, W. H., Verdi, C., Ponce, S. & Giustino, F. Polarons from first principles, without supercells. Phys. Rev. Lett. 122, 246403 (2019).
Berdiyorov, G. R. Optical properties of functionalized Ti3C2T2 (T = F, O, OH) MXene: first-principles calculations. AIP Adv. 6, 055105 (2016).
Zhu, H. et al. Screening in crystalline liquids protects energetic carriers in hybrid perovskites. Science 353, 1409–1413 (2016).
Zhang, H. et al. Highly mobile large polarons in black phase CsPbI3. ACS Energy Lett. 6, 568–573 (2021).
Giustino, F. Electron-phonon interactions from first principles. Rev. Mod. Phys. 89, 015003 (2017).
Wang, Z. et al. Tailoring the nature and strength of electron–phonon interactions in the SrTiO3 (001) 2D electron liquid. Nat. Mater. 15, 835–839 (2016).
Ito, T. et al. Electronic structure of Cr2AlC as observed by angle-resolved photoemission spectroscopy. Phys. Rev. B 96, 195168 (2017).
Zhao, S. et al. Flexible Nb4C3Tx film with large interlayer spacing for high-performance supercapacitors. Adv. Funct. Mater. 30, 2000815 (2020).
Bai, X. et al. Two-dimensional semiconducting Lu2CT2 (T = F, OH) MXene with low work function and high carrier mobility. Nanoscale 12, 3795–3802 (2020).
Yang, Y. et al. Distinguishing electronic contributions of surface and sub-surface transition metal atoms in Ti-based MXenes. 2D Mater. 7, 025015 (2020).
Zha, X. H. et al. Promising electron mobility and high thermal conductivity in Sc2CT2 (T = F, OH) MXenes. Nanoscale 8, 6110–6117 (2016).
Luo, K. et al. First-principles study on the electrical and thermal properties of the semiconducting Sc3(CN)F2 MXene. RSC Adv. 8, 22452–22459 (2018).
Lipatov, A. et al. Elastic properties of 2D Ti3C2Tx MXene monolayers and bilayers. Sci. Adv. 4, eaat0491 (2018).
Hu, T. et al. Anisotropic electronic conduction in stacked two-dimensional titanium carbide. Sci. Rep. 5, 16329 (2015).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G., Marsman, M. & Furthmüller, J. VASP (2012); https://www.vasp.at/
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Grimme, S. Semiempirical GGA‐type density functional constructed with a long‐range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Madsen, G. K. H. & Singh, D. J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71 (2006).
Xi, J., Long, M., Tang, L., Wang, D. & Shuai, Z. First-principles prediction of charge mobility in carbon and organic nanomaterials. Nanoscale 4, 4348–4369 (2012).
Slassi, A. et al. Interlayer bonding in two-dimensional materials: the special case of SnP3 and GeP3. J. Phys. Chem. Lett. 11, 4503–4510 (2020).
Acknowledgements
Financial support by the Max Planck Society is acknowledged. This work was financially supported by the European Union’s Horizon 2020 research and innovation programme (GrapheneCore3 881603) and Deutsche Forschungsgemeinschaft (MX-OSMOPED project and CRC 1415 (grant no. 417590517)). The work in Mons is financially supported by FLAG-ERA JTC 2017 project MX-OSMOPED, the Belgian National Fund for Scientific Research (FRS-FNRS), the Consortium des Équipements de Calcul Intensif (CÉCI) under grant no. 2.5020.11 and by the Walloon Region (ZENOBE Tier-1 supercomputer, grant no. 1117545). D.B. is FNRS Research Director. We thank K. Krewer, M. Grechko, M. Ballabio, X. Jia and A. Tries for fruitful discussions. We acknowledge P. Kumar, H. Kim and R. Ulbricht for constructive comments on the manuscript. We are grateful to H. Burg and R. Berger for conducting AFM image measurements. S.F. acknowledges fellowship support from the Chinese Scholarship Council (CSC). L.D.V. acknowledges support from the EU Horizon 2020 Framework Programme (grant no. 811284).
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
H.I.W. and M.B. conceived and designed the project. W.Z. conducted the terahertz spectroscopy experiments, analysed the data and performed the modelling. Z.L. performed van der Pauw conductivity measurements. B.S. and D.L. synthesized the sample and provided basic structural characterizations, under the supervision of M.Y. and X.F. S.M.G. and D.B. performed the DFT calculations. W.Z., H.I.W. and M.B. drafted the manuscript with input from all other authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Bing Xiao and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–16 and Discussion.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zheng, W., Sun, B., Li, D. et al. Band transport by large Fröhlich polarons in MXenes. Nat. Phys. 18, 544–550 (2022). https://doi.org/10.1038/s41567-022-01541-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01541-y
This article is cited by
-
MXenes with ordered triatomic-layer borate polyanion terminations
Nature Materials (2024)
-
Real-time observation of two distinctive non-thermalized hot electron dynamics at MXene/molecule interfaces
Nature Communications (2024)
-
Ultrathin MXene assemblies approach the intrinsic absorption limit in the 0.5–10 THz band
Nature Photonics (2023)
-
Electron cooling in graphene enhanced by plasmon–hydron resonance
Nature Nanotechnology (2023)
-
Simultaneous capturing phonon and electron dynamics in MXenes
Nature Communications (2022)