Abstract
A key feature of quantum spin liquids is the predicted formation of fractionalized excitations. They are expected to produce changes in the physical response, providing a way to observe the quantum spin liquid state1. In the honeycomb magnet α-RuCl3, a quantum spin liquid has been proposed to explain the behaviour observed on applying an in-plane magnetic field H||. Previous work reported that the thermal Hall conductivity took on a half-integer quantized value and suggested this as a signature of a fractionalized Majorana edge mode predicted to exist in Kitaev quantum spin liquids2. However, the temperature and magnetic-field range of the half-quantized signal2,3,4 and its association with Majorana edge modes are still under debate5,6. Here we present a comprehensive study of the thermal Hall conductivity in α-RuCl3 showing that approximately half-integer quantization exists in an extended region of the phase diagram, particularly across a plateau-like parameter regime for H|| exceeding 10 T and temperature below 6.5 K. At lower fields, the thermal Hall conductivity exhibits correlations with complex anomalies in the longitudinal thermal conductivity and magnetization, and is suppressed by cooling to low temperatures. Our results can be explained by the existence of a topological state in magnetic fields above 10 T.
Similar content being viewed by others
Main
A prime candidate for experimentally accessible quantum spin liquids is the Kitaev model, which has an exactly solvable ground state with itinerant and localized Majorana fermions7. Although they are charge-neutral, itinerant Majorana fermions carry heat and are therefore expected to contribute to thermal transport8. Applying a magnetic field gaps the bulk Majorana bands, leading to a topologically protected chiral edge current9. This edge state carries a thermal Hall conductivity per layer divided by temperature, namely, kXY2D/T = \(\frac{{{\uppi}^2k_{\mathrm{B}}}^{2}}{{6h}}\), where kB and h are the Boltzmann and Planck constants, one-half that of an equivalent electronic edge state in the quantum Hall effect due to the fractionalized nature of the Majorana fermion.
The search for material candidates of the Kitaev model has focused on Mott insulators10 with 5d4 Ir4+ and 4d4 Ru3+ having strong spin–orbit coupling on a honeycomb lattice11,12,13. Here α-RuCl3 is a prime candidate that shows antiferromagnetic zigzag order below the antiferromagnetic ordering temperature TN ≈ 7.5 K. This magnetic order is suppressed with an in-plane critical magnetic field of HC2 ≈ 7 T (refs. 2,14,15,16,17,18,19,20,21), where the magnetic moment is not yet fully saturated, revealing a region of the phase diagram where a quantum spin liquid may arise. A thermal Hall effect with a magnitude close to the half-quantized value kHQ/T (corresponding to kXY2D/T per atomic plane) was reported in the quantum spin liquid region with an in-plane magnetic field H|| along the a axis (perpendicular to the Ru–Ru bond direction)2,3,4, which was discussed as a signature of the Majorana edge state expected for the Kitaev quantum spin liquid.
To establish the presence of an edge state, however, the robustness of the half-quantized thermal Hall effect should be demonstrated over a reasonably wide range of magnetic fields and temperatures. Several studies report a plateau-like region in a field at around 5 K with a magnitude close to kHQ/T (refs. 2,3,4). These studies, however, are limited down to ~3.5 K and the plateau behaviour as a function of T is not as clear as it is in the field. The plateau-onset fields differ between studies, ranging from H|| = 7.8 T (ref. 2) to 9.9 T (ref. 3). In preparing this manuscript, we noticed that another study22 reported a broad kXY/T dome with a height appreciably smaller than kHQ/T, which was interpreted as not supporting the existence of a half-quantized plateau. Recently, anomalies in the magnetocaloric effect, specific heat and magnetic Grüneisen parameter were reported at around H|| = 10 T (refs. 23,24,25) in the spin liquid region (above HC2), suggesting that the phase diagram may be even more complex. The question of the relationship between these anomalies and the thermal Hall signature may be of fundamental importance to understand the nature of the possible field-induced quantum spin liquid, and more specifically, the possible topological edge state.
Here we present comprehensive measurements of kXY, kXX and the magnetic susceptibility (dM/dH) in a T range from 150 mK to 9 K and H|| up to 13 T (H|| along the a axis) on an α-RuCl3 single crystal, which reveals that kXY/T stays close to kHQ/T over a reasonably wide range of both temperature and magnetic field (below T = 6.5 K and from H|| ≈ 10 T up to at least 13 T), hinting at the presence of a protected half-quantized plateau. Below ~10 T, no signature of a plateau is observed and kXY/T is suppressed to zero on lowering the temperature below 6.5 K, which appears to correlate with the multiple high-field (H|| > HC2) anomalies present in both kXX and dM/dH.
Magnetic-field-induced anomalies in thermal conductivity k XX
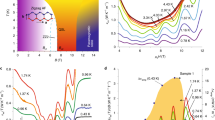
The temperature dependence of kXX reproduces the data from previous reports2 very well and displays a sharp minimum at TN = 7.5 K, which moves to lower temperatures as H|| increases and eventually fades out above HC2 = 7.1 T, tracing the extent of the antiferromagnetically ordered region (Fig. 1a,e). As a function of H||, the magnitude of kXX first decreases to a broad minimum at around 7 T and then rapidly increases (Fig. 1b). The data below 2 K reveal additional features in kXX(H||): the broad minimum splits into two at HC1 = 6.05 T and HC2 = 7.10 T. These fields coincide with two sharp peaks in dM/dH (Fig. 1c), which correspond to two reported transitions: from zigzag-ordered phase I to intermediate-ordered phase II and from phase II to the high-field paramagnetic phase23,24,25,26,27,28. The suppression of kXX at the magnetic-phase transitions is consistent with the interpretation that kXX is dominated by phonons that scatter off magnetic excitations29.
a, H||–T phase diagram of α-RuCl3 derived from features in thermal conductivity (kXX) and magnetic susceptibility (dM/dH). μ0 is the vacuum permeability. Phases I and II were previously identified as regions of long-range antiferromagnetic order (enclosed by the solid grey lines). The colour plot shows the interpolated magnitude of dM/dH (the raw data are shown in Extended Data Fig. 1). The white triangles mark the local maxima in dM/dH and dM/dT, and the orange points mark the minima in kXX. The error bars represent one standard deviation. b, Isotherms of the relative change in kXX with respect to the zero-field value as a function of the magnetic field. Antiferromagnetic transitions HC1 and HC2, as well as the features at HD1 and HD2, appear as the local minima of kXX; the feature at HP appears as a broad local maximum. c, Comparison of the sequence of anomalies in dM/dH and kXX−1 as a function of the magnetic field at 2.0 K. d, Thermal Hall conductivity divided by temperature (kXY/T) as a function of the magnetic field at 2.5 K. The data are interpolated from the dataset shown in Fig. 4, and the dashed line is the half-quantized value kHQ/T. e, kXX as a function of temperature measured in a 4He-flow cryostat, for in-plane field values ranging from 0 T to 11.3 T. For 0 T, a low-temperature dilution refrigerator measurement is superimposed. The antiferromagnetic transition temperature TN is identified as a sharp minimum. f, Calculated phonon mean free path as a function of temperature. At 12 T, the lowest-temperature phonon mean free path saturates at around 50 µm. Inset: kXX/T at high fields, demonstrating a low-temperature tendency to phonon-driven kXX ∝ T3 behaviour (the dashed line is a guide to the eye).
At higher in-plane magnetic fields and below 5 K, further anomalies can be seen in kXX, namely, a broad maximum at HP ≈ 10 T flanked by broad minima at HD1 ≈ 8.8 T and HD2 ≈ 10.7 T (Fig. 1b). Features corresponding to HD1 and HP can be clearly identified as a broad shoulder and a sudden drop in dM/dH, respectively (Fig. 1c and Extended Data Fig. 1). We argue that these high-field anomalies in kXX arise from crossovers or very weak phase transitions.
In analogy to the minima in kXX at HC1 and HC2, increased phonon scattering by soft magnetic excitations can explain the minima at HD1 and HD2. However, the anomalies at HD1 and HD2 appear broader and weaker than those at the well-defined phase transitions at HC1 and HC2 (Fig. 1b). They are enhanced on cooling to 500 mK but subsequently suppressed below 500 mK, indicative of a reduction in phonon scatterers. This suggests that HD1 and HD2 may not be well-defined phase transitions like HC1 and HC2 but highly probable crossovers with soft but finite energy excitations or alternatively very weak transitions having only a limited number of low-energy excitations involved.
Recent reports of the magnetocaloric effect23 and the magnetic Grüneisen parameter25 at temperatures above 1 K also showed anomalies near HD1 and HD2, whereas the specific heat24 at 0.67 K reported a symmetry-breaking phase transition near 10 T, a conclusion that is contested by several other measurements23,25,27,28. In the course of preparing this manuscript, we noticed another work22 in which broadly similar field-dependent structures are reported in kXX that are ascribed to quantum oscillations from underlying quasiparticles. That scenario, however, does not explain the disappearance of features in the low-temperature limit instead of the expected Lifshitz–Kosevitch behaviour (Extended Data Fig. 2) or the alignment of prominent minima with the well-established magnetic-phase transitions at HC1 and HC2.
Thermal Hall conductivity close to the half-quantized value
A strong kXY/T signal is resolved above HC2 = 7.1 T, as measured by sweeping the temperature at a fixed field (Fig. 2, T sweeps) and a magnetic field at a fixed temperature (Fig. 3, H sweeps). Great care was taken to avoid systematic errors by verifying the linear power dependence of the signal and by avoiding field hysteretic effects that may mix kXX and kXY (Extended Data Figs. 3 and 4 and Supplementary Discussion). Data from H and T sweeps are indeed consistent with each other within the given error bars, which arise from random noise in thermometry (Fig. 2, black points, and Fig. 3, thick lines). Repeated measurements were performed over multiple months to eliminate the possibility of dependence on contact geometry or sample aging and produce a fully consistent dataset.
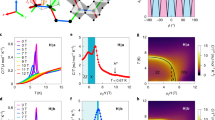
Temperature-dependent kXY/T data in order of increasing in-plane magnetic field from 7.6 T (top left) to 13.2 T (bottom right). The independent results of temperature sweeps at a fixed field (coloured points) and field sweeps at a fixed temperature (black points) are plotted together to demonstrate the high degree of consistency. From 10.3 T onwards, a kink is visible at around 6.5 K (red arrows); beyond this field, the low-temperature magnitude of kXY/T is gradually enhanced towards the half-quantized value kHQ/T (dashed line). The grey-shaded areas emphasize the temperature range below 6.5 K. The error bars represent one standard deviation.
a, Selection of kXY/T isotherms as a function of in-plane magnetic field from 250 mK to 8.5 K. A strong, complex dependence on T and H|| is observed, including enhancement at the highest fields towards the half-quantized value kHQ/T (dashed line), suppression on cooling at lower fields and non-monotonic structure for 0.25 < T < 4 K. The broad shaded lines indicate trends in the interpolated temperature sweeps at a fixed field (Fig. 2) to demonstrate consistency. b–e, Extended selection of kXY/T isotherms in order of decreasing temperature: 5.6–8.5 K (b), 3.5–5.6 K (c), 2.0–3.5 K (d) and 0.25–2.0 K (e). The error bars represent one standard deviation.
As shown in Figs. 2 and 3, kXY/T is larger than the half-quantized value kHQ/T = 0.87 mW K–2 m–1 at high temperatures and at high magnetic fields (above T = 6.5 K and HC2 = 7.1 T) and decreases to kHQ/T and below by lowering T and H||, giving rise to a region with kXY/T ≈ kHQ/T on the H||–T plane. A colour plot of kXY/T across the whole phase diagram (Fig. 4) combines data from all the H and T sweeps, which maps out the region where kXY/T is within ±20% of kHQ/T (white region). We see an L-shaped white region of kXY/T ≈ kHQ/T, which first runs vertically from T = 9.0 K to T ≈ 6.5 K at around H|| = 7.6 T and then continues horizontally from H|| ≈ 7.6 T up to at least H|| ≈ 13.2 T at around 6.5 K. The observation of an almost H||-independent kXY/T ≈ kHQ/T was also reported in previous studies at a similar temperature. In our data, it starts from a similar field of 7.6 T but extends higher to 13.2 T. As we measured a sample that was also studied elsewhere2, one may argue that the difference arises from a change in the sample quality and/or an experimental error such as dependence on contact geometry or measurement sequence. Sample degradation is unlikely because of the perfect agreement of kXX with that in the original report and reproducibility across multiple measurements (Extended Data Figs. 5 and 6). We also note that our results are reproducible with different sample-mounting geometries (Extended Data Fig. 3) and different sequences of data acquisition (H and T sweeps). Recent studies3,4 indeed report the region of kXY/T ≈ kHQ/T at higher fields than the original study, although the onset field is also higher than the original study and present study. Sample dependence is beyond the scope of this study but should be carefully checked in the future.
The most intriguing feature in Fig. 4 is the notable broadening of the white region at low temperatures with an increasing field above ~10 T, giving rise to a large, triangular white area that extends down to at least 2 K at 13 T. Does the observation of a region with kXY/T ≈ kHQ/T on the H||–T plane have a physical implication and support the presence of the topologically protected half-quantized plateau? The enhancement of kXY/T could have different origins, for instance, through (non-quantized) topological magnon5,6 or phonon30 transport. In such scenarios, a crossing may give rise to an accidental kXY/T (H||, T) ≈ kHQ/T line on the H||–T plane. In contrast, a quantized, topologically protected kXY/T(H||, T) ≈ kHQ/T plateau should exhibit insensitivity to changes in both magnetic field and temperature across and in the extended area in H|| and T.
The extended nature of kXY/T (H||, T) ≈ kHQ/T above 10 T represented by the white triangular plane in Fig. 4 argues against an accidental crossing scenario and hints at a half-quantized plateau and hence a Majorana edge state in α-RuCl3. The corresponding T-sweep data (Fig. 2) shows that for fields greater than 10.3 T, a kink-like singularity in the T dependence of kXY/T appears at ~6.5 K (Fig. 2, red arrows). Notably, at the kink, kXY/T is always ~kHQ/T, implying that the magnitude of kHQ/T has special importance in the system. On lowering T, the kink is followed by an almost T-independent kXY/T ≈ kHQ/T region, reminiscent of an incipient half-quantized T plateau and then by a rapid decrease to zero. The width of the T-plateau-like region gradually expands on increasing the field from 10.3 T, giving rise to the white triangle in Fig. 4.
The narrow L-shaped white region below H|| ≈ 10 T (Fig. 4), on the other hand, represents a ‘line’ of kXY/T (H||, T) ≈ kHQ/T, which is clearly demonstrated by the T and H sweeps in Figs. 2 and 3. Along the vertical white region in Fig. 4, kXY/T is smoothly suppressed on cooling at 7.6 T (Fig. 2) and continuously decreases through kHQ/T with decreasing H|| in the H sweeps (Fig. 3). Along the horizontal white region at around 6.5 K, kXY/T shows a plateau in the H sweep at 6.5 K (Fig. 3), but continuously decreases through kHQ/T in the T sweeps up to ~10 T. It is not obvious why kXY/T crosses kHQ/T at a constant temperature of 6.5 K. Nevertheless, because of the line character of the region of kXY/T (H||, T) ≈ kHQ/T, the white region (Fig. 4) below H|| ≈ 10 T is probably due to accidental crossing.
Low-temperature suppression of k XY/T
What is the origin of the rapid suppression of kXY/T to zero at low temperatures below 12 T (Fig. 4, red-coloured region)? Within this red region, weak structures are observed: three vertical streaks of minima (deeper red) at around H|| = 7.0, 9.5 and 11.0 T and two vertical streaks of maxima (brighter red) at around H|| = 8.5 and 10.0 T branching out from the white region at T = 6.5 K. As shown in Figs. 1d and 4, the fields of the three minima apparently coincide with the critical field HC2 and the two high-field anomalies at HD1 and HD2 observed in kXX and dM/dH. The maximum at ~10 T reflects the singularly weak T dependence of kXY/T at H|| = 10.3 T (Fig. 2) and coincides with HP. These correlations suggest that the high-field magnetic crossovers/transitions are related to the suppression of kXY/T at low temperatures.
Interpolated magnitude of kXY/T normalized by kHQ/T across the H||–T phase diagram. In the colour scheme, white represents a thermal Hall conductivity within 20% of the half-quantized value. The grey lines trace the antiferromagnetic phase transitions (for reference). The two low-temperature minima in kXY/T at HD1 and HD2 are indicated by arrows.
If a half-quantized thermal Hall plateau arises from a chiral Majorana edge mode8, it was theoretically shown that the coupling between a phonon bath and the edge mode31,32 is necessary to observe the plateau in the presence of dominant phonon conductivity. Phonons must be in the diffuse rather than the ballistic scattering regime. If phonons experience a crossover from the diffuse to the ballistic regimes on cooling or under a magnetic field, the thermal Hall signal from the Majorana edge mode should vanish due to the decoupling of phonons and edge modes, which might account for the low-temperature suppression of kXY/T. From the estimation of the phonon mean free path (lph) from kXX as a function of H|| and T, however, we may exclude the phonon–edge mode decoupling scenario as the origin of low-temperature suppression of kXY/T below kHQ/T from 7 to 12 T.
kXX approaches a T3 power law at the highest fields and lowest temperatures (Fig. 1f), consistent with phonon transport limited by a temperature-independent scattering length. The calculated lph reaches ~50 µm at the lowest temperatures, which is somewhat smaller than the sample width of ~1 mm (Fig. 1f and Extended Data Fig. 7), meaning that phonon transport at low temperatures is still marginally in the diffuse regime. Furthermore, the fact that the regions of suppressed kXY/T coincide with the minima in kXX, that is, regions with the shortest lph, argues against the decoupling scenario. The low-temperature enhancement of kXY/T to kHQ/T on increasing the magnetic field is accompanied by an increase in lph, the opposite of what would be expected from phonon–edge mode decoupling. We also note that the decoupling scenario appears to be contrary to a report in which the half-quantized plateau is only observed in samples with high (phonon) thermal conductivity4.
Recently, the scenario of purely phonon-driven thermal Hall was proposed based on the discovery of a large thermal Hall effect in non-magnetic SrTiO3 and the correlation between the T dependence of kXX and kXY in RuCl3 (ref. 30). In addition, in the magnetic insulator Ba3CuSb2O9, a thermal Hall angle (tan(θH) ≈ 10−4), similar to that of RuCl3, was claimed to arise from the phonon thermal Hall effect alone33. The observed suppression of kXY/T at low temperatures and its correlation with kXX are in line with a phonon-driven scenario. Both show an overall increase on increasing the field, with dip-like suppressions at HD1 and HD2. Although a phonon-only scenario could explain these correlations between kXX and kXY, it is not clear how it would naturally explain the observed plateau-like behaviour of kXY/T close to kHQ/T.
The identification of possible topological phase transitions into and out of the half-quantized state still remains an open question23,24,25,27,28. For the former, unveiling the nature of high-field anomalies may be the key question to be addressed. The high-field transition out of the half-quantized state, if it exists, must be at a field higher than 13 T. A measurement of kXY/T to much higher fields is, therefore, highly desired. Alternative mechanisms leading to an enhancement of kXY/T, such as a topological magnon-driven5,6 or phonon-driven30 Hall effect, have been proposed. Our results do not exclude those scenarios but pose them a challenge to explain the plateau-like behaviour close to half-quantization.
Methods
Samples
Large, thin (~2.5 mm × 1.3 mm × 17 µm), high-quality single crystals of α-RuCl3 from the same growth batches as those reported in ref. 2 were measured. The sample under investigation for thermal Hall measurements has a confirmed half-quantized Hall plateau in that report, where it was labelled as ‘sample 2’. A second sample with a similarly high thermal conductivity was used for magnetic susceptibility measurements.
Thermal conductivity was measured using a steady-state three-thermometer setup. For the temperature range of 1.8–9.0 K, Cernox CX-1050 chip thermometers (Lake Shore) were used in a 4He cryostat. For the temperature range of 150 mK to 3 K, ruthenium oxide chip thermometers were used in a dilution fridge. In each case, thermometers were calibrated in situ against a field-calibrated reference thermometer. A 10 kΩ NiCr resistive heater was used to apply heater power. The sample was free standing with its ‘cold’ edge mounted with Apiezon N grease onto a LiF single crystal, which was attached with silver paint onto a copper mount and cooled by the cryostat. Several copper mounts machined at different angles were used to allow for measurements in fixed tilted fields.
Geometrical error affects the measurement due to the finite contact sizes and uncertainty in determining the exact crystal dimensions. We estimate the resulting systematic uncertainty in kXY/T to be around 10%, which is in addition to the random error due to thermometry noise (error bars shown in Figs. 2 and 3).
We adopt the usual convention that the crystal a axis is perpendicular to Ru–Ru bonds, the b axis lies along the Ru–Ru bonds and the c axis is perpendicular to the honeycomb plane. The magnetic field was applied at either 70° from the c axis (4He) or 90° from the c axis (dilution refrigerator), with the in-plane field component in the a axis. The amplitude of kXX, as well as the measured transition fields (HC1, HC2, HD1 and HD2), were confirmed to reproduce at the same values of H|| for these two field angles (Extended Data Fig. 6); therefore, the two datasets are presented as one. The field angle was determined under an optical microscope with 1° precision. Heat was always applied along the a axis.
Over the course of these measurements, the crystal was thermally cycled between room temperature and <4.2 K for 14 times; each time, identical values of kXX were measured, indicating that sample deterioration over time is negligible. The measurement of kXX is additionally in very close agreement with that previously measured in Kyoto (Extended Data Fig. 5).
Magnetization measurements above 2 K were performed using a Physical Property Measurement System vibrating sample magnetometry option (Quantum Design), and below 1 K using a custom-built Faraday force magnetometer on a dilution refrigerator (Extended Data Fig. 1). For all the magnetization data, the applied field was parallel to the crystal a axis.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
References
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Kasahara, Y. et al. Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 559, 227–231 (2018).
Yokoi, T. et al. Half-integer quantized anomalous thermal Hall effect in the Kitaev material candidate α-RuCl3. Science 373, 568–572 (2021).
Yamashita, M., Kurita, N. & Tanaka, H. Sample dependence of the half-integer quantized thermal Hall effect in a Kitaev candidate α-RuCl3. Phys. Rev. B 102, 220404 (2020).
McClarty, P. A. et al. Topological magnons in Kitaev magnets at high fields. Phys. Rev. B 98, 060404 (2018).
Zhang, E. Z., Chern, L. E. & Kim, Y. B. Topological magnons for thermal Hall transport in frustrated magnets with bond-dependent interactions. Phys. Rev. B 103, 174402 (2021).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Nasu, J., Yoshitake, J. & Motome, Y. Thermal transport in the Kitaev model. Phys. Rev. Lett. 119, 127204 (2017).
Motome, Y. & Nasu, J. Hunting Majorana fermions in Kitaev magnets. J. Phys. Soc. Jpn 89, 012002 (2020).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Trebst, S. & Hickey, C. Kitaev materials. Phys. Rep. 950, 1–37 (2022).
Winter, S. M., Li, Y., Jeschke, H. O. & Valentí, R. Challenges in design of Kitaev materials: magnetic interactions from competing energy scales. Phys. Rev. B 93, 214431 (2016).
Takagi, H., Takayama, T., Jackeli, G., Khaliullin, G. & Nagler, S. E. Concept and realization of Kitaev quantum spin liquids. Nat. Rev. Phys. 1, 264–280 (2019).
Baek, S. H. et al. Evidence for a field-induced quantum spin liquid in α-RuCl3. Phys. Rev. Lett. 119, 037201 (2017).
Wang, Z. et al. Magnetic excitations and continuum of a possibly field-induced quantum spin liquid in α-RuCl3. Phys. Rev. Lett. 119, 227202 (2017).
Zheng, J. et al. Gapless spin excitations in the field-induced quantum spin liquid phase of α-RuCl3. Phys. Rev. Lett. 119, 227208 (2017).
Banerjee, A. et al. Excitations in the field-induced quantum spin liquid state of α-RuCl3. npj Quant. Mater. 3, 8 (2018).
Johnson, R. D. et al. Monoclinic crystal structure of α-RuCl3 and the zigzag antiferromagnetic ground state. Phys. Rev. 92, 235119 (2015).
Kubota, Y., Tanaka, H., Ono, T., Narumi, Y. & Kindo, K. Successive magnetic phase transitions in α-RuCl3: XY-like frustrated magnet on the honeycomb lattice. Phys. Rev. B 91, 094422 (2015).
Yadav, R. et al. Kitaev exchange and field-induced quantum spin-liquid states in honeycomb α-RuCl3. Sci. Rep. 6, 37925 (2016).
Sears, J. A. et al. Magnetic order in α-RuCl3: a honeycomb-lattice quantum magnet with strong spin-orbit coupling. Phys. Rev. B 91, 144420 (2015).
Czajka, P. et al. Oscillations of the thermal conductivity observed in the spin-liquid state of α-RuCl3. Nat. Phys. 17, 915–919 (2021).
Balz, C. et al. Finite field regime for a quantum spin liquid in α-RuCl3. Phys. Rev. B 100, 60405 (2019).
Tanaka, O. et al. Thermodynamic evidence for field-angle dependent Majorana gap in a Kitaev spin liquid. Preprint at https://arxiv.org/abs/2007.06757v1 (2020).
Bachus, S. et al. Thermodynamic perspective on field-induced behavior of α-RuCl3. Phys. Rev. Lett. 125, 97203 (2020).
Balz, C. et al. Field-induced intermediate ordered phase and anisotropic interlayer interactions in α-RuCl3. Phys. Rev. B 103, 174417 (2021).
Ponomaryov, A. N. et al. Nature of magnetic excitations in the high-field phase of α-RuCl3. Phys. Rev. Lett. 125, 37202 (2020).
Schönemann, R. et al. Thermal and magnetoelastic properties of α-RuCl3 in the field-induced low-temperature states. Phys. Rev. B 102, 214432 (2020).
Hentrich, R. et al. Unusual phonon heat transport in α-RuCl3: strong spin-phonon scattering and field-induced spin gap. Phys. Rev. Lett. 120, 117204 (2018).
Li, X., Fauqué, B., Zhu, Z. & Behnia, K. Phonon thermal Hall effect in strontium titanate. Phys. Rev. Lett. 124, 105901 (2020).
Vinkler-Aviv, Y. & Rosch, A. Approximately quantized thermal Hall effect of chiral liquids coupled to phonons. Phys. Rev. X 8, 31032 (2018).
Ye, M., Halász, G. B., Savary, L. & Balents, L. Quantization of the thermal Hall conductivity at small Hall angles. Phys. Rev. Lett. 121, 147201 (2018).
Sugii, K. et al. Thermal Hall effect in a phonon-glass Ba3CuSb2O9. Phys. Rev. Lett. 118, 145902 (2017).
Acknowledgements
We thank Y. Kasahara and Y. Matsuda for insightful discussions and M. Dueller and K. Pflaum for technical assistance. The work done in Germany has been supported in part by the Alexander von Humboldt Foundation. H. Tanaka and N.K. have been supported by JSPS KAKENHI via grant nos. JP17H01142 and JP19K03711, respectively. H. Takagi has been supported in part by JSPS KAKENHI via grant no. JP17H01140.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
J.A.N.B., R.R.C., Y.M. and H. Takagi conceived the research. N.K. and H. Tanaka synthesized the single crystals. J.A.N.B. and R.R.C. designed and performed the thermal conductivity experiments. Y.M. designed and performed the magnetic susceptibility experiments. J.A.N.B., R.R.C., Y.M. and H. Takagi analysed the data and participated in the writing of the paper. All the authors contributed to the manuscript preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks David Mandrus and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Magnetization isotherms and phase transitions.
Field dependences of dM/dH which were used to construct the phase diagram in Fig. 1a (main text). a, isotherms of dM/dH, with every curve offset by 0.003 emu/mol for clarity. Phase transitions out of the antiferromagnetic phases HC1, HC2 are identified by peaks in dM/dH, whereas HP coincides with a drop in dM/dH. b, isotherms of d2M/dH2, where the feature at HP is identified as a local minimum. HP shifts only minimally in field upon heating, and is no longer resolved at 10 K. Curves are offset by 8×10−4 emu/mol T for clarity.
Extended Data Fig. 2 Temperature dependence of high-field features in kXX.
The amplitude of high-field features in kXX is expressed as (kXX - kbg)/kbg, where kbg is a smooth background fit which passes through the points where kXX has greatest field derivative (as discussed in Ref. 22). a, field dependence (kXX - kbg)/kbg for temperatures between 70 mK (dark blue) and 2.5 K (dark red). b, temperature dependence of (kXX - kbg)/kbg at the local minimum at ~8.6 T and the local maximum at ~9.7 T, indicated by arrows in panel a. The amplitude at constant field (dashed lines), and the amplitudes at the fields of maximum amplitude (solid lines and markers) differ slightly due to a temperature-dependent phase shift. The amplitudes initially increase upon cooling but peak around 1 K and then rapidly collapse to zero down to the lowest measured temperature, in marked contrast to the Lifshitz-Kosevitch behavior expected for conventional quantum oscillations.
Extended Data Fig. 3 Excluding error arising from Hall contact offset.
a,b, photographs of sample 2 with wires attached in different configurations 1 and 2. The latter configuration was the one used for the measurements shown in the main text. Purple dashed line are guides to the eye to help identify the contact offset. c, measured Hall contact offset expressed as ΔTY/ ΔTX (%) at 0 T, showing the expected inverse offsets for the two configurations. In the absence of an offset, ΔTY/ ΔTX would be zero (dashed line). d, isotherms of kXY/T at 3.0 K for both contact configurations, displaying the same features at HD1 and HD2. e, isotherms of kXY/T for configuration 1 at multiple temperatures, demonstrating the reproducibility of all the main features observed with configuration 2 (main text, Fig. 3).
Extended Data Fig. 4 Excluding power dependence in kXY.
Repeated measurements at different levels of heater power demonstrate that the measured thermal conductivity and thermal Hall conductivity are independent of the applied heater power. a, Hall temperature gradient normalized by heater power (ΔTY/P) for two independent isotherms at 3 K, one of which was performed at half the standard heater power (red markers, ΔTX /T ≈ 5%). The two curves overlap as expected. b, the temperature dependence of kXY/T at 8.64 T is compared for two T sweeps, one of which was performed at half power (green markers, ΔTX /T ≈ 5%), together with full-power H sweeps. All curves overlap within error. c, temperature dependence of kXY/T is compared for two T sweeps at 13.2 T, one of which was performed at double the usual power (ΔTX /T ≈ 20%), together with normal-power H sweeps. The data overlap within the (substantially field-enhanced) error bars.
Extended Data Fig. 5 Reproducibility of thermal conductivity measurements.
Comparison of three independent measurements of the thermal conductivity (kXX) of sample 2. Red circles: data measured in Kyoto, Solid blue circles: data taken in a dilution refrigerator in Stuttgart, open blue circles: data taken in a 4He flow cryotstat in Stuttgart. Each measurement had slightly modified contact placements.
Extended Data Fig. 6 Temperature and magnetic field-angle dependence of the thermal conductivity above 2.0 K.
a, field dependence of kXX up to 12 T for the temperature range 2.0 K – 8.6 K. The sharp features in the field dependence of kXX seen at low temperature rapidly disappear upon heating above 3.0 K. At high temperatures, the field dependence displays a single, broad minimum around 7 T. At 8.6 K, which is above the ordering temperature TN = 7.5 K, the field dependence is dramatically weakened, although a high field upturn persists at this temperature. b, comparison of the field dependence of kXX at 2.0 K and 2.5 K, at field angles of 70° (markers) and 90° (lines) with respect to the c-axis. The near-perfect overlap of the data sets demonstrates the insensitivity to magnetic field angle.
Extended Data Fig. 7 Calculated phonon mean free path across the H||,T phase diagram.
Contour plot of the calculated phonon mean free path lph = 3 kXX / C v, where C is the phonon specific heat per unit volume and v is the average phonon velocity. We assume a magnetic field-independent low temperature phonon specific heat with magnitude Cph/T3 = 1.22 mJ mol−1K−4 as reported in Ref. 24. The phonon velocity is estimated using the Debye relation \(v = \left( {\frac{{2\pi ^2k_B^4}}{{5\beta \hbar ^3}}} \right)^{\frac{1}{3}} \approx 1700m/s\) where β = Cph/T3 as before. The grey lines trace the antiferromagnetic phase transitions, for reference.
Supplementary information
Supplementary Information
Supplementary Discussion and Fig. 1.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Extended Data Fig. 1
Statistical source data.
Source Data Extended Data Fig. 2
Statistical source data.
Source Data Extended Data Fig. 3
Statistical source data.
Source Data Extended Data Fig. 4
Statistical source data.
Source Data Extended Data Fig. 5
Statistical source data.
Source Data Extended Data Fig. 6
Statistical source data.
Source Data Extended Data Fig. 7
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bruin, J.A.N., Claus, R.R., Matsumoto, Y. et al. Robustness of the thermal Hall effect close to half-quantization in α-RuCl3. Nat. Phys. 18, 401–405 (2022). https://doi.org/10.1038/s41567-021-01501-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-021-01501-y
This article is cited by
-
Magnon thermal Hall effect via emergent SU(3) flux on the antiferromagnetic skyrmion lattice
Nature Communications (2024)
-
Large oscillatory thermal hall effect in kagome metals
Nature Communications (2024)
-
Thermal Hall effects due to topological spin fluctuations in YMnO3
Nature Communications (2024)
-
Phonons bend to magnetic fields
Nature Physics (2024)
-
Planar thermal Hall effect from phonons in a Kitaev candidate material
Nature Communications (2024)