Abstract
In a burning plasma state1,2,3,4,5,6,7, alpha particles from deuterium–tritium fusion reactions redeposit their energy and are the dominant source of heating. This state has recently been achieved at the US National Ignition Facility8 using indirect-drive inertial-confinement fusion. Our experiments use a laser-generated radiation-filled cavity (a hohlraum) to spherically implode capsules containing deuterium and tritium fuel in a central hot spot where the fusion reactions occur. We have developed more efficient hohlraums to implode larger fusion targets compared with previous experiments9,10. This delivered more energy to the hot spot, whereas other parameters were optimized to maintain the high pressures required for inertial-confinement fusion. We also report improvements in implosion symmetry control by moving energy between the laser beams11,12,13,14,15,16 and designing advanced hohlraum geometry17 that allows for these larger implosions to be driven at the present laser energy and power capability of the National Ignition Facility. These design changes resulted in fusion powers of 1.5 petawatts, greater than the input power of the laser, and 170 kJ of fusion energy18,19. Radiation hydrodynamics simulations20,21 show energy deposition by alpha particles as the dominant term in the hot-spot energy balance, indicative of a burning plasma state.
Similar content being viewed by others
Main
Inertially confined fusion plasmas at the US National Ignition Facility (NIF) use a rocket-like ablation effect to compress millimetre-sized capsules filled with deuterium–tritium (DT) fuel to hundreds of billions of times the pressure of Earth’s atmosphere, the conditions required for fusion and subsequent alpha heating. The rocket is created when the outer layers of the capsules containing nuclear fuel are ablated by an intense X-ray radiation bath that is generated when the 192 laser beams of the NIF illuminate the inside of a gold-lined depleted uranium X-ray conversion cavity called a ‘hohlraum’. The remaining capsule mass and fuel are accelerated towards the centre of the DT gas core at extreme implosion velocities (vimp) of nearly 400 km s–1. During stagnation, the kinetic energy of the imploding shell and DT fuel is converted into internal energy in a dense fuel layer surrounding a central lower density ‘hot spot’ where most of the fusion reactions occur. Symmetric compression of the DT fuel surrounding the hot spot is essential for providing inertial confinement and time for the alpha particles to redeposit their energy before the system explodes and rapidly cools as it expands, as well as achieving adequate areal densities required for sufficient alpha deposition. This redeposition of alpha-particle energy back into the hot spot leads to further fusion reactions and amplified neutron yield.
The DT fuel is more compressible when its entropy is lower, described by the fuel adiabat (α = plasma pressure/Fermi pressure). A low adiabat is accomplished by raising the ablation pressure (Pabl) in steps before accelerating the shell inwards, with each step adding a limited amount of entropy through the shock compression of previously shocked fuel. After the maximum ablation pressure is achieved, it is important to maintain the ablation pressure as late into the implosion as possible to minimize fuel decompression before the formation of the hot spot. The total number of neutrons produced from the fusion reactions, or neutron yield (Y), of an inertially confined fusion plasma can be related to a few key implosion properties:
where implosions of a larger scale (S) can result in a greater number of fusion reactions if the other aspects of the implosion can be maintained, which is called the ‘HYBRID’ strategy1. Measurable perturbations such as non-sphericity in the imploding shell and fuel can reduce the efficiency of the implosion to do mechanical work on the hot spot, as described in equation (1) by the residual (or left-over) kinetic energy (RKE)22.
Shorter-wavelength hydrodynamic instabilities lead to the mixing of capsule material into the DT hot spot, resulting in radiative loss or reduced compression and lower yield. This is captured in the implosion efficiency term η (ref. 23; Extended Data Table 1). The degree to which hydrodynamic instabilities can impact the implosion depends on the target design as well as features in the target that can seed instabilities such as defects in the capsule generated during fabrication, the fill tube used to introduce DT24 and a support structure that holds the capsule in the centre of the hohlraum25. The exponents in equation (1) were derived for an implosion where bremsstrahlung radiation losses balance the alpha-particle heating; although they are expected to change as the plasma starts to become dominated by alpha heating, this equation shows the relative importance of these critical parameters and can be used to guide the design space.
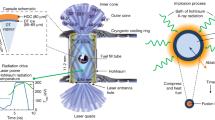
In this work, we tripled the energy from fusion reactions compared with previous experiments by increasing the scale (S) of implosion by 10–15% along with maintaining the hot-spot pressure required for inertial-confinement fusion and other critical implosion properties described in equation (1), a strategy outlined elsewhere1. Driving larger implosions to similar velocities as smaller-scale implosions9,10 and using the same amount of laser energy requires the development of more efficient smaller hohlraums with lower radiation losses from the reduced surface area. This results in a smaller case-to-capsule ratio (CCR) or smaller hohlraum diameter for a given capsule size. Such designs are more challenging for controlling implosion symmetry, as there is less room for the laser beams to propagate beyond the expanding capsule material and wall plasma, resulting in a radiation drive deficit deep in the interior of the hohlraum. As illustrated in Fig. 1a, the more intense ‘outer’ laser beams reach the wall closer to the ends of the hohlraum, creating an expanding ‘bubble’26,27 of gold plasma that intercepts the ‘inner’ beams aimed deeper towards the hohlraum waist. The resulting spatial non-uniformity in radiation temperature drives an aspherical implosion that will reduce the implosion efficiency. Larger capsules also use thicker ablators to protect against the longer times over which hydrodynamic instabilities can grow. To achieve the same shock-merger locations with thicker shells, the laser power steps needed to be more separated in time, leading to a longer-duration laser pulse and more hohlraum plasma filling.
Implosion symmetry control in low-gas-fill hohlraums is accomplished via CBET12,14,15,16 from the outer laser beams (44° and 50°) to the inner beams (23° and 30°) to compensate for reduced inner-beam propagation later in time. The amount of transfer is controlled by detuning the wavelengths of the inner and outer cones relative to each other (Δλ). a, HYBRID-E cylindrical hohlraum (left) uses more CBET than the I-Raum-shaped hohlraum (right) to achieve similar X-ray flux symmetry on the capsule in part due to the larger capsule and longer pulse length. Compared with a cylinder with the same laser pulse and beam pointing, the I-Raum ‘pockets’ radially displace the expanding wall plasma caused by the outer beams, delaying interception of the inner beams. The top half of each hohlraum shows the calculated positions of the wall and capsule materials at peak power (6 ns) from radiation hydrodynamic HYDRA simulations with individual laser rays overlaid. The gold-lined depleted uranium hohlraum is orange, the HDC ablator is grey, the DT ice layer is red and the DT fill gas is light blue. The laser rays are coloured based on their power, with some rays gaining power through CBET (more red) before becoming absorbed (more blue). The left sides depict simulations without wavelength detuning, whereas the right sides include Δλ, illustrating enhanced inner-beam propagation due to CBET from a representative 44° beam to a 23° beam. Laser absorption in the gold bubble and low-density ablated HDC is visible as the ray powers transition through white from red to blue. The rays terminate (dark blue) near where the plasma density is high enough for substantial laser absorption. The bottom half of each hohlraum depicts nominal beam pointing and relative target dimensions between the two designs as visualized by VISRAD38. Further details regarding target dimensions and design parameters are given in Extended Data Fig. 5 and Extended Data Table 2, respectively. b, Energy-flow diagrams illustrating the CBET process in more detail. The four cones of beams pass energy amongst themselves due to CBET from wavelength detuning (Δλ = inner-beam (10,530.05 Å) wavelength – outer-beam (10,528.5 Å) wavelength at the fundamental neodymium glass laser frequency, 1ω) and local plasma flows, resulting in a net gain for the inner beams and a net loss for the outer beams. c, Measured hohlraum radiation temperatures using filtered X-ray diodes (top) and the delivered laser pulses (bottom) for one high-performing shot from each design.
Implosion symmetry was previously controlled in small-CCR hohlraums28,29 by transferring energy between laser beams, or cross-beam energy transfer (CBET). In this process, light is scattered from one crossing laser beam to the other through an ion acoustic wave that is resonantly driven by the overlapping laser beams when they have different wavelengths or in the presence of plasma flow.
However, high levels of laser–plasma-interaction instabilities reduced the hohlraum efficiency by scattering laser light back out of the hohlraum. This was largely due to the application of large amounts of energy transfer in hohlraums with higher levels of helium gas fill, designed to mitigate the expanding wall by generating a counter-pressure. These configurations also resulted in large amounts of inferred high-energy electrons30 that can prematurely heat the DT fuel and raise the adiabat. It was also difficult to predict and control the radiation symmetry over the entire implosion, resulting in aspherical implosions with degraded performance28,29,31. Since then, hohlraums with lower gas-fill densities of 0.03–0.60 mg cm–3 and larger CCRs were developed to reduce laser back-scatter and high-energy electron production9,10,32,33,34. These designs varied the relative laser powers and energies to control the symmetry with no intentional energy transfer between the laser beams. This limits the total laser energy and ultimately the maximum scale that can currently be fielded, since a fraction of the beams will be at less than the maximum capability.
Here we introduce two designs that enable increasing the capsule scale within the limits of the NIF laser and providing symmetry control in more efficient, smaller-CCR hohlraums: transferring energy between the laser beams by changing their relative wavelengths in hohlraums with low helium gas fill (HYBRID-E)11,13 and using a shaped (non-cylindrical) hohlraum to delay plasma filling for better inner-beam propagation (I-Raum)17. The first technique, as illustrated in Fig. 1, transfers energy from the ‘outer’ beams to the ‘inner’ beams, increasing the power delivered to the waist of the hohlraum, in a low-back-scatter environment. Even in the presence of large amounts of transfer (up to two times increase in the inner-beam power), the measured laser energy coupled to the hohlraum is ≥98% (ref. 11) and the inferred level of hot electrons is more than an order of magnitude lower than previously seen in high-gas-fill hohlraums using wavelength detuning. Reduced back-scatter and laser–plasma-interaction instabilities in the presence of large amounts of transfer creates a stronger observed sensitivity of implosion symmetry to wavelength detuning, allowing for radiation-symmetry control throughout the drive history11,22. The HYBRID-E design demonstrates the use of wavelength detuning in a hohlraum with a gas-fill density of 0.3 mg cm–3. The I-Raum17 concept adds engineered pockets in the wall to displace the plasma blowoff generated by the outer beams radially outwards, delaying expansion into the inner beams compared with a cylinder having the same pointing and pulse shape; further, wavelength detuning was used to control symmetry. Both platforms used data-driven models26 to guide the hohlraum design choices that impact the extent of ‘bubble’ and implosion symmetry (Methods).
The top half of Fig. 1a shows the hydrodynamic simulations of HYDRA20,21 radiation of the two designs midway through peak power at 6 ns after the start of the laser pulse (Methods provides a description of the simulation methodology). The colour contour shows the material boundary: gold shows the expanding hohlraum wall plasma; grey, the expanding capsule ablator; red, the inwards-moving cryogenic DT fuel layer; and light blue, the DT gas. The so-called ‘gold bubble’26,27 launched by the outer (44° and 50°) beams can be seen intercepting the inner beams (23° and 44°) and interacting with the capsule blowoff. Simulated laser rays, coloured by the spatially varying power as energy is exchanged or absorbed, illustrate the impact of CBET with wavelength detuning (for example, for HYBRID-E Δλ = inner-beam (10,530.05 Å) wavelength – outer-beam (10,528.5 Å) wavelength at the fundamental neodymium glass laser frequency (1ω), before conversion to the third harmonic at 351 nm.) by comparing simulations with no detuning (left) to simulations that include detuning (right). With CBET, a substantial amount of power is transferred from the outer to inner beams, enhancing the drive at the hohlraum waist. The white band of inner-beam absorption in the simulations without CBET traces the position of the expanding gold bubble and also indicates laser absorption in the capsule ablator. Figure 1b also shows the total calculated energy transfer between the laser cones for the two designs. Lower energy transfer between the beams was required in the I-Raum design due to the outwards bubble displacement by the pockets, the smaller-scale capsule and the shorter laser pulse length as a result of the thinner DT ice layer (with a shorter shock-transit time). Despite the I-Raum pockets, the position of the bubble is similar for the two designs in this work as a result of other design differences governing the bubble growth26,27. The measured radiation temperatures (Tr; Fig. 1c) are similar, as expected for hohlraums with nearly the same surface area. The laser power histories for each design with different ‘epochs’ labelled are also shown in Fig. 1c.
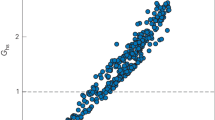
Figure 2 shows that the designs presented in this work (red and blue points) realized the benefit of higher capsule-absorbed energy (to increase the energy delivered to the hot spot) compared with previous high-density carbon (HDC) campaigns or Bigfoot implosions (grey points) by operating at a larger scale, but only when improving or maintaining the other metrics in equation (1). The expected extrapolation in performance to higher levels of capsule-absorbed energy from a smaller-scale HDC campaign implosion N170601 (ref. 35) are also shown, which were calculated using radiation hydrodynamic simulations in two and three dimensions. Here the symmetry (Extended Data Fig. 1), stability (Extended Data Fig. 2), implosion velocity, adiabat and inflight ablation pressure were maintained in the scaling.
Neutron yield as a function of capsule-absorbed energy for the I-Raum (blue, closed symbols; N210220 and N201122) and HYBRID-E (red, closed symbols; N210207, N210307 and N201101) experiments in this work together with previous HDC campaign experiments9 (grey points), and two- and three-dimensional simulations of scaling the capsule-absorbed energy from N170601 (ref. 35) (solid black lines). The capsule-absorbed energy quoted for each experiment is derived from simulations, and the error bars represent the maximum range over which the simulated bang time remains consistent with the measurements when fine-tuning the X-ray drive to calibrate the experiments. The experiments in this work follow the predictions when the other important implosion properties in the yield equation (equation (1)) are also maintained, such as velocity, adiabat, ‘coast time’, stability and symmetry. Then, the capsule-absorbed energy can be efficiently converted into hot-spot internal energy and pressure. Additional experiments in the I-Raum and HYBRID-E campaigns led to the optimization in this work (open symbols; N190217, N191105, N201011, N200229 and N191110) but were compromised by known degradations to the terms in equation (1), as discussed in the main text.
The present experiments are not directly scaled hydrodynamically from N170601, however, and improve on certain aspects of the implosion, for example, low-mode asymmetries. Therefore, the present experiments are not expected to necessarily follow these trend lines, but they provide a guideline for potential improvement when scaling up the implosion size at a similar adiabat and implosion velocity.
The larger-scale I-Raum (blue) and HYBRID-E (red) designs absorb more energy but use larger hohlraums (lower Tr) compared with N170601 to maintain symmetry and require thicker ablators or DT layers to maintain stability (Methods), which results in similar implosion velocities (Table 1). Due to the mergers of the first and second shocks occurring inside the DT ice at ~10 μm larger radius than the ice–gas interface, the fuel adiabats at peak velocity were a little higher for both designs (3.0−3.2) compared with N170601 (2.5) (Table 1), and the ‘coast times’ were longer. However, the low-mode asymmetry, namely, mode 2 of the Legendre decomposition of the hot spot in N170601 that was kept constant in the extrapolation to be more conservative, was improved in the highest-performing I-Raum and HYBRID-E experiments (Methods provides more details).
The progression of design or experimental optimization within the HYBRID-E and I-Raum campaigns is shown through several example points (open and closed symbols), which illustrates that the benefit of increased capsule energy can only be realized if the pressure is maintained through the other terms in equation (1). Both designs have worked to maintain the late-time ablation pressure but continued optimization is ongoing. A metric for this is the ‘coast time’36 or the time that the implosion has to decompress when the radiation drive is decreasing (Table 1 and Methods), which was reduced between experiments N201011 and N201101 by extending the laser pulse and resulted in more than thrice the neutron yield. Experiment N200229 had more coupled energy to the capsule than the experiments in this paper using a larger-scale capsule (inner radius, 1,100 μm), but the ‘coast time’ was ~1.7 times longer, the symmetry was substantially worse (very oblate) and there were many more seeds for high-mode perturbations present in the ablator19. The other non-optimized I-Raum and HYBRID-E experiments in Fig. 2 (open symbols) are impacted by reduced implosion efficiency due to hydrodynamic instabilities or low-mode asymmetries compared with the highest performers (closed symbols) (Methods provides additional details).
By increasing the hot-spot energy, with more coupled energy to the implosion and also maintaining the hot-spot pressure, we have created a burning plasma state in the laboratory. The criteria for achieving a burning plasma state are investigated using analytical models18 and key quantities derived from high-resolution two-dimensional HYDRA simulations that reproduce the performance metrics (Methods and Table 1). The mechanical PdV work (EPdV) on the hot spot and total DT fuel from the imploding DT ice and ablator material are directly extracted from the simulations (Methods). The net cumulative hot-spot energies as a function of time relative to the time of peak neutron production (‘bang time’) are shown in Fig. 3, where the corresponding insets show the simulated densities and temperatures at bang time. A comparison of simulations and measurements of the compressed DT shell is provided in Methods. Simulations where alpha-particle heating is artificially turned off (no-α) are also shown and enable more accurate tracking of the mechanical work.
The coloured lines show the calculated cumulative hot-spot energies as a function of time for each shot. Each panel shows data from one ‘burn on’ simulation that includes alpha deposition (α-on; solid curves) and one ‘burn off’ simulation in which alpha particles leave the problem without depositing energy (no-α; dashed curves). The time axis has been scaled relative to the ‘bang time’, or time of peak neutron production, for each simulation with alpha deposition included. The respective (α-on, α-off) bang times in nanoseconds for shots N201101, N201122, N210207 and N210220 are (9.35, 9.30), (9.08, 9.03), (8.67, 8.60) and (8.80, 8.70), respectively. The total hot-spot internal energy (black) is increased due to hydrodynamic compression (PdV work; blue) up until stagnation and any alpha heating (green), and is reduced due to bremsstrahlung radiation losses (red) and hydrodynamic expansion after stagnation (PdV work; blue). For these experiments, after entering the burning plasma regime, alpha-particle heating outstrips the radiation losses, becoming the dominant term in the hot-spot energy balance. The insets illustrate the simulated configuration of the hot spot and dense surrounding shell with density (g cm–3) on the left half and ion temperature (keV) on the right half. The hot spot is defined as a fixed collection of DT mass, tracked over time, that gives 98% of the neutron production at peak burn. The maximum (density (g ml–1), ion temperature (keV)) values for shots N201101, N201122, N210207 and N210220 are (350, 7.31), (450, 6.49), (350, 8.40) and (450, 7.20), respectively.
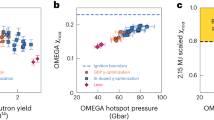
We now demonstrate that these four experiments enter the burning plasma regime based on several different metrics. We find that the net energy from alpha-particle heating at bang time (\({E}_{\upalpha }^{{\mathrm{a}}} ,{{\mathrm{b}} }\)) is greater than the energy from work done on the hot spot (EPdV) at bang time for three out of the four experiments and is thus the dominant source in the energy balance equation (EIE = Eα + EPdV − Erad − Econd). (See Table 1 for an explanation of the nomenclature; superscript ‘a’ indicates the quantity taken at peak neutron production, or ‘bang time’, and superscript ‘b’ indicates the quantity is extracted from the data shown in Fig. 3.) Although the simulated metric for all the four experiments is met (\({E}_{\upalpha }^{{\mathrm{a}},{\mathrm{b}}}/{E}_{P{\mathrm{d}}V,{\rm{no}}{\mbox{-}} \upalpha }\,\) > 1), the more simplistic metric of ~0.5Eα/EPdV,HS,no-α > 1 is only met by the two highest-performing experiments. The net energy from alpha-particle heating is calculated to be greater than the energy-loss terms from radiation and conduction (Erad and Econd, respectively) for all the experiments. Here the radiation losses are extracted from the simulations and conduction losses are inferred from the energy balance equation.
Other metrics for burning plasma include the ratio of the total energy produced by the alpha particles to the total DT kinetic energy (Eα/KE > 1), which is met by all the four experiments. Additionally, the burning plasma criteria for yield amplification2 and increase in yield due to alpha-particle heating (Yamp ≥ 3.5) are met by all four experiments, and the fuel gain criterion (Gfuel)28, the ratio of the total fusion yield to the PdV work done on the hot spot and compressed DT ice (DT EPdV,no-α), is met by three experiments. Finally, the Hurricane model for assessing a burning plasma state using the simulated hot-spot areal density, ion temperature and implosion velocity (vcond/vimp) is met by all the four experiments. In summary, N210207 meets all the criteria and also dominates the energy balance equation including hot-spot internal energy, two experiments meet all the criteria and all the four experiments meet several of the criteria for burning plasma.
Future experiments will continue to optimize these platforms by reducing the sources of high-mode perturbations (for example, capsule defects and DT fill tube), reduce the adiabat by improving the shock timing and the rate of the final rise to peak laser power, and improve the hot-spot pressure or energy coupling with even more efficient hohlraums or by varying the DT ice thickness (Methods). These improvements are calculated to have large impacts in performance, for example, reducing the ‘coast time’ with a smaller laser entrance hole (LEH) is calculated to improve the performance by almost two times. As this paper was being finalized, a new experiment in the HYBRID-E series on 8 August 2021 produced ~1.35 MJ of fusion yield and a capsule gain of ~6, a significant achievement for the field of ICF (announced by our institution in a press release37); this experiment will be described in a future publication. In addition, we continue to study the tradeoffs between the ablator and DT thickness ratios for large-scale implosions, which is important for understanding limitations on design choices for future designs that additionally increase the scale beyond the designs in this paper.
Methods
Additional design parameters
The HYBRID-E and I-Raum designs use similar hohlraum surface areas (2.5 cm2 for HYBRID-E and 2.6 cm2 for I-Raum) and length, and the same size of LEHs—the main source of radiation loss, which led to similar radiation temperatures (Fig. 1). The HYBRID-E shots N201101 and N210207 use wavelength separations of 1.75 and 1.55 Å, respectively, between the outer and inner beams to implode an HDC capsule (inner radius, 1,050 μm) filled with a 65-μm-thick frozen DT ‘ice’ layer (density ≈ 0.25 g cm–3) with sufficient drive at the hohlraum equator. The I-Raum shots N201122 and N210220 use 260 μm recessed pockets together with 0.5 Å wavelength separation to drive a diamond capsule (inner radius, 1,000 μm) filled with a 55-μm-thick frozen DT ‘ice’ layer. The outer surface areas of the ablators were 16 mm3 for HYBRID-E and 14.7 mm3 for I-Raum. Extended Data Fig. 5 provides additional hohlraum design dimensions.
Both designs used an HDC ablator (capsule) with either nanocrystalline or microcrystalline structure39 and a W dopant layer to act as a preheat shield from high-energy hohlraum X-rays and provide a more stable Atwood number35,40. Both designs increase the ablator thickness compared with smaller-scale implosions9,10, which is required when hydroscaling (hydrodynamic scaling) a design to shield against the longer time for hydrodynamic instabilities to grow. The I-Raum design used an ablator that was thicker (~14% in effective thickness) than the increase in capsule scale (~10% increase in capsule radius) compared with the HDC campaign9. The ‘effective’ thickness accounts for the difference in crystalline structures between the designs (microcrystalline for HDC and Bigfoot), which changes the HDC density. Nanocrystalline ablators have lower density and require thicker layers for the same ‘effective’ layer thickness compared with microcrystalline HDC, conserving the total initial ablator mass to provide similar amounts of ablator mass remaining following ablation from the radiation drive.
The HYBRID-E design increased the ablator thickness compared with the HDC campaign design but was thinner than the ratio of the increase in capsule scale (~10% thicker versus an increase in capsule scale of ~15%). However, the thickness of HYBRID-E is consistent with a separate recent prescription for hydroscaling35, which accounts for the fact that the penetration depth of the X-ray radiation drive does not hydrodynamically scale. This choice was initially made, given the current radiation drive, to enable driving a thicker DT ice layer than the hydroscaled version (~18% increase in thickness compared with a ~15% increase in capsule scale) to a similar velocity for the purpose of providing more protection against high-mode perturbations from known capsule defects present in these specific capsule batches, and has been previously shown to be effective13. However, as found elsewhere35, the scaled ablator thickness should be thinned by 5 μm for every 20% increase in scale, which is consistent with the HYBRID-E design thickness as a hydroscale of the HDC campaign9 and Bigfoot10. The I-Raum design uses the same ice thickness as the HDC design, thinner than hydrodynamically scaled with the capsule radius, which may enable higher convergence and velocities for a given ablator mass remaining given a good capsule quality. Experiments at the inner-radius scale of 1,050 μm using thinner DT ice layers (10 μm thinner) are currently being tested. Preliminary results show faster implosion velocities (+10–15 km s–1) at similar ablator mass remaining and levels of hot-spot mixing. The tradeoff in ablator and DT ice thicknesses versus directly hydroscaling the HDC campaign9,35 will be tested in future experiments using even more efficient hohlraums (Methods). These studies are imperative for understanding the design limitations of additionally increasing capsule scale within the experimental capability of the NIF.
To maintain linear growth factors (relative growth of a perturbation at peak implosion velocity compared with its initial size) at both interfaces when hydroscaling, the prescription from another study35 is to reduce the dopant concentration by the reciprocal of the scale increase. For the HYBRID-E N210207, the dopant was lowered to 0.28% tungsten (W), consistent with this scaling as compared with the HDC campaign design (0.33% W and a similar layer thickness). HYBRID-E experiment N201101 used an HDC capsule with higher optical depth (dopant concentration times the dopant layer thickness) compared with the HDC campaign design (Extended Data Table 2), but performed similar to N210207 when accounting for the difference in the hot spot and dense fuel symmetry. The doped layer in the I-Raum design was thicker than that for HYBRID-E or than the scale of the HDC campaign or Bigfoot designs, which resulted in lower growth factors at the fuel–ablator interface and higher growth factors at the ablation front compared with HDC or HYBRID-E (Extended Data Fig. 2). Uncertainties in the hohlraum atomic models used in this work could lead to growth factors at the ablation front that are ~200 higher than those shown in Extended Data Fig. 2 for both designs. Another factor when designing implosion stability is the early part of the laser pulse (called the ‘picket’), which launches the first shock and impacts the steepness of the ablation-front profile. Higher early time ablation pressure can reduce perturbation growth factors at the ablation front. The HYBRID-E and I-Raum designs had similar first-shock radiation temperatures, which was achieved with a lower picket power for HYBRID-E due to the smaller CCR where the outer beams hit the hohlraum wall compared with I-Raum. This led to similar first shock strengths (>12 Mbar), which were designed to avoid the refreezing of the diamond behind the shock front and in the reflected shock, as well as similar fuel adiabats at peak velocity.
A short ‘coast time’—nominally the time between the maximum radiation temperature and bang time (maximum compression)—is important for maintaining the ablation pressure and achieving high hot-spot pressures and fuel compression36, but is more challenging with a fixed laser energy and for maintaining symmetry. A ramped (or ‘drooping’) laser pulse10,41 was used in HYBRID-E, which was designed to help maintain the late-time ablation pressure at the larger scale and enabling the full use of the NIF laser (Extended Data Fig. 1). For the experiments in this paper, the coast times (defined as the time between the bang time and the time at which Tr falls to 95% of the maximum Tr) are similar but shorter for HYBRID-E due to the ramped laser power at the end of the pulse. A metric related to coast time is the deceleration time or time between the peak implosion velocity and bang time. This is approximately Rpv/vimp, where Rpv is the radius at peak velocity and vimp is the implosion velocity but can be slightly different than the calculated deceleration time due to velocity changes over the deceleration time (Table 1).
The increased deceleration rate associated with a short coast increases the rate at which implosion kinetic energy is turned into internal energy. For fixed vimp, a larger-scale implosion will have a longer deceleration time; therefore, it is necessary to compensate for that by keeping the late-time hohlraum temperature hot (maintaining a higher late-time ablation pressure) by extending the duration of the laser pulse shape (Table 1), which was longer for HYBRID-E versus I-Raum accounting for the scale factor. In the limit of zero coast time, the pressure inside the implosion, which is responsible for deceleration, rapidly overwhelms the ablation pressure outside the implosion, and the impact of further extending the radiation drive is reduced. The designs in this paper have not yet seen a reduction in impact when reducing the coast time, and further improvements can be made in both platforms.
DT dense-shell non-uniformities, or ρR variations, at peak compression that can arise from early time radiation flux asymmetries are minimized by controlling the ‘foot’ of the radiation drive—the time until the rise to peak power—using cone-fraction balancing. The cone fraction is defined as the ratio of the inner laser power over the total laser power. The normalized Legendre decompositions of the radiation flux moment (P2/P0) at the foot of the pulse (before the rise to peak laser power) is designed to be as close to zero as possible, but allowed to vary during the peak of the pulse to enable the full use of NIF (33% cone fraction), and may deviate from zero at early times due to as-shot laser delivery (Extended Data Fig. 1). During the peak of the laser pulse, the inner beams can easily propagate initially and the radiation flux asymmetry has a negative sign in P2/P0 (or higher drive at the waist of the hohlraum). Near the end of the peak power, the inner beams have more difficulty propagating beyond the expanding wall and ablator material, and the sign of the P2/P0 flux changes. Changing the radiation flux asymmetry during the peak of the pulse is not detrimental to the implosion as long as the flux asymmetry can be balanced to provide a symmetric final dense shell and hot spot where the symmetry of the implosion itself is not fluctuating. This is assessed in simulations and experiments through the shape of the implosion at ~200 μm compared with peak compression at ~40 μm. The P2/P0 flux asymmetry is similar in magnitude between the designs but the sign for HYBRID-E changes faster due to the longer pulse and larger capsule as well as requiring more transfer early in the pulse to compensate for the late-time P2/P0 sign change. The primary impact of increasing the CBET is to shift the P2/P0 radiation flux during the peak of the pulse to more negative values, as well as maintaining symmetry during the ‘foot’, and does not substantially change the slope of the time-dependent P2/P0 (ref. 11).
Until the time when substantial plasma filling and LEH closure come into play, radiation hydrodynamic simulations tuned to previous data are very predictive in designing symmetric shocks viewed along the pole and equator, a metric for ‘foot’ P2 flux asymmetry (Methods). Even when using CBET to control symmetry during the peak of the pulse, radiation drive symmetry during the foot of the pulse can be accurately predicted and modelled with no artificial multipliers in low-gas-fill hohlraums11,12,42. The P4/P0 flux asymmetry is mainly determined by the CCR, picket power and outer-beam pointing. Changes between the designs lead to slightly worse calculated P4/P0 flux asymmetry for I-Raum compared with HYBRID-E in the ‘foot’ of the laser pulse.
Continued discussion on optimization and reproducibility
The progression of the design or experimental optimization within the HYBRID-E and I-Raum campaigns is shown in Fig. 2 through several example points (open and closed symbols), illustrating the benefit of increased capsule energy only when the pressure is also maintained through the other terms in equation (1). In addition to the reduction in ‘coast time’ from the inner radius of 1,100 to 1,050 μm for HYBRID-E implosions, the stability and low-mode asymmetries were also improved in the campaign optimizations for HYBRID-E and I-Raum. For example, I-Raum experiments N190217 versus N191105 also showed the impact of improving high-mode instabilities on the neutron yield by reducing the number of ablator defects and improving the design stability using a higher picket. An implosion efficiency term η (ref. 23 and Extended Data Table 1) estimates the reduction in yield due to radiative loss from the hot spot and cold fuel, which was reduced when the capsule quality was increased between these experiments. Capsule defects that can seed high-mode perturbations, other than the support tent and DT fill tube, are still present in the HYBRID-E experiments19, and further improvement could lead to higher performance19. Both designs are predicted to have increased performance with reduction in DT fill tube size, which can result in ablator mix into the hot spot19; experiments to test this are ongoing.
Improving the low-mode radiation drive asymmetries, which is challenging at a larger scale, also enabled the efficient conversion of capsule-absorbed energy to hot-spot internal energy. This is shown by the increase in performance of I-Raum designs N201122 and N210220 compared with N191105, which improved the symmetry by introducing a small amount of wavelength detuning (Δλ = 0.5 Å). A metric for improvement in symmetry is the level of oblateness of the implosion, namely, mode 2 coefficient of the Legendre decomposition of the 17% intensity contour of the primary neutron image (P2) (Extended Data Table 1).
The HYBRID-E experiments also improved symmetry by reducing the amount of wavelength detuning between experiments N201101 (1.75 Å) versus N210307 and N210207 (1.55 Å), improving performance by 40–70%. Both designs control the time-dependent radiation flux symmetry during the early part of the laser pulse using the fine-tuning of the laser power balance. Although the intrinsic low-mode asymmetries were improved to reach high performance, as-shot laser power variations and target non-uniformities resulted in odd-mode asymmetries that are calculated to impact the performance, and are worse for I-Raum experiments19. Additional tests to reduce these non-uniformities are ongoing.
HYBRID-E experiment N210307 was similar to N210207 with regard to the hohlraum configuration, capsule size, ice thickness, shock timing, wavelength separation and velocity, but used different HDC capsules having a larger number of known degradations in the ablator that can seed hydrodynamic instabilities. There were also some differences in the calculated hydrodynamic stability due to differences in the as-delivered percentage of the W dopant level and crystal structure of the ablator. However, these experiments performed similarly, even with differences in the capsule quality and differences in the low-mode asymmetry (primary neutron image P2), which provides confidence in the reproducibility of the burning plasma results for near-neighbour designs. In I-Raum experiment N210220, compared with N201122, an intentional laser imbalance was attempted to mitigate the known sources of Legendre mode 1 asymmetry in the implosion, seeded by hohlraum diagnostic windows and ablator thickness non-uniformity. Detailed analyses and understanding of these experiments are ongoing.
Simulation methodology
Optimizations to the target designs were studied through numerical simulations (HYDRA21) and using semi-empirical models26 to guide design choices relating to the radiation drive symmetry during the peak of the laser pulse, which is difficult to model. Once adjusted using power multipliers, numerical simulations are generally predictive in calculating the implosion energetics for finite changes in the design space, for example, laser pulse power history or capsule parameter changes in the same hohlraum configuration. These simulations can be extrapolated further in the design space for exploring new hohlraum configurations, but have more uncertainty and may need to be recalibrated. The numerical simulations can also very accurately predict the radiation drive symmetry during the ‘foot’ of the pulse11,12, until the rise to peak laser power, in the presence of large amounts of CBET specifically enabled by using low-gas-fill hohlraums. However, the simulation cannot accurately and consistently model the radiation flux symmetry during the main part of the laser pulse (peak power). Controlling the symmetry during this part of the pulse is critical for achieving adequate implosion symmetry. As part of the HYBRID strategy1, we use data-driven models26 to predict the symmetry during this part of the pulse and to guide design choices such as the hohlraum size, laser-beam pointing, amount of energy in the outer beams during the early part of the pulse and so on. To additionally estimate the impact of wavelength detuning on implosion symmetry, we combine this data-driven model26 with an experimentally measured sensitivity of implosion symmetry to wavelength detuning 11.
The numerical simulation methodology used for platform design (idealized conditions before the shot) and post-shot analysis (incorporating information from the experiment such as the delivered laser pulse and measured hohlraum and capsule dimensions) is performed in a two-step process. The radiation hydrodynamic simulations include multigroup radiation transport; non-local thermodynamic equilibrium (NLTE) atomic kinetics (required for modelling high-atomic-number hohlraums and capsule ablation) using detailed configuration accounting (LLNL 2010 DCA atomic models)43; three-dimensional ray tracing for laser-light interaction with the hohlraum wall and plasma as well as a detailed account of the transfer of energy between beams; detailed equation of state and opacity models; Monte Carlo transport of the fusion products; and electron thermal conduction from Livermore equation of state (LEOS) tables with a flux limiter of 0.15neTevTe, where ne is the electron density, Te is the electron temperature and vTe is the electron thermal velocity. First, lower-spatial-resolution integrated capsule and hohlraum simulations model the radiation drive with spatial, temporal and photon-energy resolution (Fig. 1). These simulations require the calibration of drive magnitude and symmetry during the peak of the pulse to match experimental measurements in separate focused or calibration experiments for each platform11,17,44. If some aspect of the design is changed, such as the size of the LEH, the calibrated models are used to extrapolate the plasma conditions. These calibration experiments can also be revisited with parameters closer to the modified design.
The radiation drive is extracted from these lower-resolution integrated hohlraum and capsule simulations and imposed on higher-resolution capsule-only simulations45,46 in two dimensions with symmetry along the axis (Extended Data Fig. 4), which can resolve a larger number of modes (≤200). Also included are models for the engineering features in the target (capsule support, fill tube, roughness of the capsule and ice layer) as well as low-mode perturbations from the radiation flux asymmetries. The calculations for the four experiments in this paper use some combination of known perturbations, which may be different between the experiments, but under-predict the performance when all the known perturbations are applied. Thus, the choice of applied perturbations to match the level of observed neutron production may impact the relative agreement to other key metrics. Extended Data Fig. 4 shows a comparison of the simulated (middle) to measured fluence-compensated down-scattered neutron image47 (top), which provides a picture of the burn-averaged compressed dense shell surrounding the hot spot for the experiments in this paper. Although the three-dimensional features cannot be captured by two-dimensional simulations, the main features and sizes of the compressed shells are generally reproduced (Table 1) for a comparison with other implosion metrics. For example, the higher-density features at the poles for N210207 and N201122 are replicated by the simulations and low-density region at the north pole for N201101 since the as-shot laser asymmetry is captured by the simulations. The simulated images for density and temperature corresponding to these calculations at peak neutron production are shown in Extended Data Fig. 4, bottom. The visible simulated mode 4 perturbation in experiment N210207 is not a result of the capsule support tent model, but the applied roughness spectrum coupled with the low-mode radiation drive asymmetries.
To calculate the amount of PdV work done on the hot spot, we track a constant mass that encompasses 98% of the neutron production at peak neutron emission. The pressure and change in volume of this mass (with volume weighting) are calculated to give the cumulative net PdV work on the hot spot, radiation loss from the hot spot and alpha heating of the hot spot as a function of time (Fig. 3). This hot-spot boundary is chosen to incorporate enough mass such that conduction losses may be neglected. We use the PdV work calculated at the time of peak neutron production for the simulations where alpha-particle heating is artificially turned off (‘burn off’). This is done so that the estimate of mechanical work done on the hot spot by the imploding fuel and shell is not influenced by alpha heating. Ratios of alpha-heating energies to the work done on the hot spot at ‘bang time’, and in total, are the main metrics for burning plasma.
The yield amplification (Yamp) ratio of the neutron yield in simulations that allow alpha particles to redeposit energy to simulations in which this is artificially prohibited is another metric for the impact of alpha-particle heating on the implosion and burning plasma. The performance of HYBRID-E and I-Raum designs can be matched in two dimensions using a subset of the known degradations, and under-predict the performance when all the degradations are applied. To assess the impact of perturbation choice on the calculated yield amplification, various simulations of these designs including different perturbation choices or magnitude of perturbations were performed, for example, variations in surface roughness, tent model, fill tube model, low-mode asymmetries, capsule-thickness non-uniformities and mix model at the fuel–ablator interface. Extended Data Fig. 3 shows a clear trend in Yamp with total neutron yield for HYBRID-E (red) and I-Raum (blue) even for simulations with varying calculated down-scattered ratios, a measure of the areal density of the compressed shell. The red and blue lines in Extended Data Fig. 3 correspond to the total yields for the experiments in this paper, showing that all the four experiments are calculated to meet the yield amplification criteria for a burning plasma of >3.5. Other metrics for alpha-particle heating include the increase in simulated hot-spot mass, deuterium–tritium (DT) and deuterium–deuterium (DD) ion temperatures, hot-spot pressure and hot-spot internal energy compared with simulations where alpha-particle heating is artificially turned off (no-α) (Table 1).
Future studies
Future studies are aimed at continuing to optimize the key metrics from equation (1). Fielding smaller LEHs from the present value of 3.10–3.64 mm will improve the late-time ablation pressure by maintaining higher Tr later in time (lower radiation losses). In addition, smaller LEH hohlraums can achieve similar radiation temperatures to the designs in this work at lower power, which enables longer-duration pulses even with fixed available laser energy, further improving the late-time ablation pressure. The smaller LEH hohlraums can also be used to field thicker ablator implosions, for example, thickness of more than 4 μm at the inner-radius scale of 1,050 μm and thickness of more than 10 μm at the inner-radius scale of 1,100 μm, which is expected to improve the design stability and enable higher implosion velocities with similar levels of ablator mass remaining. Based on the modest levels of CBET presently needed to control symmetry, we expect achieving adequate symmetry in a smaller LEH hohlraum to be manageable. The impact of the thickness of the DT ice layer is also being investigated. Simulation studies that increased implosion convergence through reductions in the implosion adiabat, as well as controlling the tendency of more hydrodynamic instability, are also being performed. Finally, experiments to further increase the implosion scale by 5–30% and maintaining the other critical properties in equation (1) are underway.
Data availability
Raw data were generated at the National Ignition Facility and are not available to the general public. Derived data supporting the findings of this study are available from the corresponding authors upon request.
Code availability
The simulation codes used in this manuscript are not available to the general public.
References
Hurricane, O. A. et al. Beyond alpha-heating: driving inertially confined fusion implosions toward a burning-plasma state on the National Ignition Facility. Plasma Phys. Control. Fusion 61, 014033 (2019).
Betti, R. et al. Alpha heating and burning plasmas in inertial confinement fusion. Phys. Rev. Lett. 114, 255003 (2015).
Hurricane, O. A. et al. Approaching a burning plasma on the NIF. Phys. Plasmas 26, 052704 (2019).
National Academies of Sciences, Engineering, and Medicine Final Report of the Committee on a Strategic Plan for U.S. Burning Plasma Research (National Academies Press, 2019).
Lindl, J. D., Haan, S. W., Landen, O. L., Christopherson, A. R. & Betti, R. Progress toward a self-consistent set of 1D ignition capsule metrics in ICF. Phys. Plasmas 25, 122704 (2018).
Christopherson, A. R. et al. Theory of ignition and burn propagation in inertial fusion implosions. Phys. Plasmas 27, 052708 (2020).
Atzeni, S. & Meyer-ter-Vehn, J. The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter (Oxford Univ. Press, 2004).
Moses, E. The National Ignition Facility: an experimental platform for studying behavior of matter under extreme conditions. Astrophys. Space Sci. 336, 3–7 (2011).
Le Pape, S. et al. Fusion energy output greater than the kinetic energy of an imploding shell at the National Ignition Facility. Phys. Rev. Lett. 120, 245003 (2018).
Casey, D. T. et al. The high velocity, high adiabat, ‘Bigfoot’ campaign and tests of indirect-drive implosion scaling. Phys. Plasmas 25, 056308 (2018).
Kritcher, A. L. et al. Achieving record hot spot energies with large HDC implosions on NIF in HYBRID-E. Phys. Plasmas 28, 072706 (2021).
Kritcher, A. L. et al. Energy transfer between lasers in low-gas-fill-density hohlraums. Phys. Rev. E 98, 053206 (2018).
Zylstra, A. B. et al. Record energetics for an inertial fusion implosion at NIF. Phys. Rev. Lett. 126, 025001 (2021).
Kruer, W. L., Wilks, S. C., Afeyan, B. B. & Kirkwood, R. K. Energy transfer between crossing laser beams. Phys. Plasmas 3, 382–385 (1996).
Glenzer, S. H. et al. Symmetric inertial confinement fusion implosions at ultra-high laser energies. Science 327, 1228–1231 (2010).
Michel, P. et al. Tuning the implosion symmetry of ICF targets via controlled crossed-beam energy transfer. Phys. Rev. Lett. 102, 025004 (2009).
Robey, H. F., Berzak Hopkins, L., Milovich, J. L. & Meezan, N. B. The I-Raum: a new shaped hohlraum for improved inner beam propagation in indirectly-driven ICF implosions on the National Ignition Facility. Phys. Plasmas 25, 012711 (2018).
Zylstra, A. B. et al. Burning plasma achieved in inertial fusion. Nature https://doi.org/10.1038/s41586-021-04281-w (2022).
Ross, J. S. et al. Experiments conducted in the burning plasma regime with inertial fusion implosions. Preprint at https://arxiv.org/pdf/2111.04640 (2021).
Marinak, M. M. et al. Advances in HYDRA and its applications to simulations of inertial confinement fusion targets. EPJ Web Conf. 59, 06001 (2013).
Marinak, M. M. et al. Three-dimensional HYDRA simulations of National Ignition Facility targets. Phys. Plasmas 8, 2275–2280 (2001).
Kritcher, A. L. et al. Metrics for long wavelength asymmetries in inertial confinement fusion implosions on the National Ignition Facility. Phys. Plasmas 21, 042708 (2014).
Pak, A. et al. Impact of localized radiative loss on inertial confinement fusion implosions. Phys. Rev. Lett. 124, 145001 (2020).
Baker, K. L. et al. Fill tube dynamics in inertial confinement fusion implosions with high density carbon ablators. Phys. Plasmas 27, 112706 (2020).
Nagel, S. R. et al. Effect of the mounting membrane on shape in inertial confinement fusion implosions. Phys. Plasmas 22, 022704 (2015).
Callahan, D. A. et al. Exploring the limits of case-to-capsule ratio, pulse length, and picket energy for symmetric hohlraum drive on the National Ignition Facility Laser. Phys. Plasmas 25, 056305 (2018).
Ralph, J. E. et al. The influence of hohlraum dynamics on implosion symmetry in indirect drive inertial confinement fusion experiments. Phys. Plasmas 25, 082701 (2018).
Lindl, J. D. et al. Review of the national ignition campaign 2009–2012. Phys. Plasmas 21, 020501 (2014).
Hurricane, O. A. et al. Fuel gain exceeding unity in an inertially confined fusion implosion. Nature 506, 343–348 (2014).
Dewald, E. L. et al. Hot electron measurements in ignition relevant hohlraums on the National Ignition Facility. Rev. Sci. Instrum. 81, 10D938 (2010).
Kritcher, A. L. et al. Integrated modeling of cryogenic layered highfoot experiments at the NIF. Phys. Plasmas 23, 052709 (2016).
Berzak Hopkins, L. F. et al. First high-convergence cryogenic implosion in a near-vacuum hohlraum. Phys. Rev. Lett. 114, 175001 (2015).
Turnbull, D. et al. Symmetry control in subscale near-vacuum hohlraums. Phys. Plasmas 23, 052710 (2016).
Divol, L. et al. Symmetry control of an indirectly driven high-density-carbon implosion at high convergence and high velocity. Phys. Plasmas 24, 056309 (2017).
Clark, D. S. et al. Three-dimensional modeling and hydrodynamic scaling of National Ignition Facility implosions. Phys. Plasmas 26, 050601 (2019).
Hurricane, O. A. et al. On the importance of minimizing ‘coast-time’ in X-ray driven inertially confined fusion implosions. Phys. Plasmas 24, 092706 (2017).
Bishop, B. National Ignition Facility experiment puts researchers at threshold of fusion ignition. Lawrence Livermore National Laboratory https://www.llnl.gov/news/national-ignition-facility-experiment-puts-researchers-threshold-fusion-ignition (2021).
MacFarlane, J. J. VISRAD—A 3-D view factor code and design tool for high-energy density physics experiments. J. Quant. Spectrosc. Radiat. Transfer 81, 287–300 (2003).
Williams, O. A. & Nesládek, M. Growth and properties of nanocrystalline diamond films. Phys. Stat. Sol. A 203, 3375–3386 (2006).
Berzak Hopkins, L. et al. Increasing stagnation pressure and thermonuclear performance of inertial confinement fusion capsules by the introduction of a high-Z dopant. Phys. Plasmas 25, 080706 (2018).
Berzak Hopkins, L. et al. Toward a burning plasma state using diamond ablator inertially confined fusion (ICF) implosions on the National Ignition Facility (NIF). Plasma Phys. Control. Fusion 61, 014023 (2019).
Pickworth, L. A. et al. Application of cross-beam energy transfer to control drive symmetry in ICF implosions in low gas fill hohlraums at the National Ignition Facility. Phys. Plasmas 27, 102702 (2020).
Patel, M. V., Scott, H. A. & Marinak, M. M. The HYDRA DCA atomic kinetics package. In American Physical Society, 52nd Annual Meeting of the APS Division of Plasma Physics Vol. 52, NO5.008 (APS, 2010).
Jones, O. S. et al. A high-resolution integrated model of the National Ignition Campaign cryogenic layered experiments. Phys. Plasmas 19, 056315 (2012).
Clark, D. S. et al. Detailed implosion modeling of deuterium-tritium layered experiments on the National Ignition Facility. Phys. Plasmas 20, 056318 (2013).
Clark, D. S. et al. Capsule modeling of high foot implosion experiments on the National Ignition Facility. Plasma Phys. Control. Fusion 59, 055006 (2017).
Casey, D. T. et al. Fluence-compensated down-scattered neutron imaging using the neutron imaging system at the National Ignition Facility. Rev. Sci. Instrum. 87, 11E715 (2016).
Acknowledgements
We thank B. Coppi (MIT), S. C. Cowley (PPPL), D. Whyte (MIT), J. Hammer (LLNL), M. Farrell (GA) and J. Kline (LANL) for thoughtful discussions. The contributions of NIF operations and target fabrication teams to the success of these experiments are gratefully acknowledged. This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under contract DE-AC52-07NA27344. This document was prepared as an account of work sponsored by an agency of the US government. Neither the US government nor Lawrence Livermore National Security, LLC, or any of their employees, makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer or otherwise does not necessarily constitute or imply its endorsement, recommendation or favouring by the US government or Lawrence Livermore National Security, LLC. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the US government or Lawrence Livermore National Security, LLC, and shall not be used for advertising or product endorsement purposes. LLNL-JRNL-821690-DRAFT
Author information
Authors and Affiliations
Contributions
A.L.K.: HYBRID-E design lead, integrated hohlraum group lead and wrote sections of paper. C.V.Y.: present I-Raum design lead and wrote sections of paper. H.F.R.: original I-Raum design lead. C.R.W.: capsule/instability physics. A.B.Z.: hot-spot analysis lead, HYBRID-E experimental lead. O.A.H.: capsule scale/burning plasma strategy, theory, zero-dimensional hot-spot models and wrote sections of paper. D.A.C.: empirical hohlraum P2 model and hohlraum strategy. J.E.R.: N201101 and N210207 experimentalist and shot responsible individual (shot RI). J.S.R.: I-Raum experimental lead and N201122 shot RI. K.L.B.: hybrid shot RI. D.T.C.: HYBRID shot RI. D.S.C.: capsule/instability physics. T.D.: HYBRID shot RI. L.D.: three-dimensional hot-spot analysis. M.H.: HYBRID shot RI. L.B.H.: HDC design and campaign lead. S.L.P.: HYBRID shot RI. N.B.M.: advanced hohlraum lead. A.P.: HYBRID and I-Raum shot RI as well as physics of capsule engineering defects. P.K.P.: one-dimensional hot-spot analysis as well as Yamp and GLC inference. R.T.: HYBRID shot RI. S.J.A.: capsule microstructure physics. P.A.A.: hohlraum physics. L.J.A.: engineering and targets. B.B.: penumbral X-ray diagnostic. D.B.: computational physics. L.R.B.: X-ray framing camera. R.B.: inertially confined fusion (ICF) physics/ignition theory. S.D.B.: cryo-layering. J.B.: diamond capsule fabrication and materials science. R.M.B.: real-time neutron activation detector’s nuclear diagnostic. N.W.B.: neutron diagnostics. E.J.B.: project engineering. D.K.B.: diagnostics. T.B.: capsule fabrication and metrology. T.M.B.: cryo-layering. M.W.B.: project engineering. P.M.C.: deuterium–tritium equation-of-state measurements. B.C.: HYDRA code development. T.C.: laser plasma instability physics. H.C.: gated laser entrance hole X-ray diagnostic. C.C.: target fabrication planning. A.R.C.: ignition theory. J.W.C.: capsule fabrication. E.L.D.: experiments. T.R.D.: capsule physics. M.J.E.: program management. W.A.F.: hohlraum physics. J.E.F.: 2DConA image analysis. D.F.: nuclear diagnostics. J.A.F.: magnetic recoil spectrometer nuclear diagnostic. J.A.G.: ensemble simulations. M.G.J.: magnetic recoil spectrometer diagnostic. S.H.G.: ICF physics. G.P.G.: nuclear diagnostics. S.H.: capsule physics and cryogenic deuterium–tritium ice-layer analysis. K.D.H.: neutron diagnostics. G.N.H.: experiments. B.A.H.: capsule physics. J.H.: computational physics. E.H.: nuclear time-of-flight diagnostics. J.E.H.: laser delivery quality control and improvements. V.J.H.: laser delivery quality control and improvements. H. Herrmann: gamma diagnostics. M.C.H.: programme management. D.E.H.: hohlraum physics and CBET studies in HYBRID-C. D.D.H.: capsule physics. J.P.H.: X-ray diagnostics. W.W.H.: management. H. Huang: capsule fabrication. K.D.H.: ensemble simulations. N.I.: X-ray diagnostics. L.C.J.: X-ray diagnostics. J.J.: neutron diagnostics. O.J.: hohlraum physics. G.D.K.: HYDRA code development. S.M.K.: neutron diagnostics. S.F.K.: X-ray diagnostics and analysis. J.K.: diagnostic management. Y.K.: gamma diagnostics. H.G.K.: gamma diagnostics. V.G.K.: neutron diagnostics. C.K.: capsules. J.M.K.: HYDRA code development. M.K.G.K.: ensemble simulations. J.J.K.: targets. B.K.: ensemble simulations. O.L.L.: velocity analysis. S.L.: laser–plasma instability (PF3D) code development. D.L.: NIF facility management. N.C.L.: optical diagnostics. J.D.L.: ICF physics. T.M.: ICF physics. M.J.M.: X-ray diagnostics. B.J.M.: mode 1 analysis and back-scatter. A.J.M.: diagnostic management. S.A.M.: integrated design physics. A.G.M.: X-ray diagnostics. M.M.M.: HYDRA code development lead. D.A.M.: X-ray diagnostics. E.V.M.: X-ray diagnostics. L.M.: capsule physics. K.M.: gamma diagnostics. P.A.M.: LPI physics. M.M.: optical diagnostics. J.L.M.: hohlraum physics. J.D.M.: hohlraum physics. A.S.M.: neutron diagnostics. J.W.M.: hohlraum physics. T.M.: neutron and gamma diagnostics. K.N.: project engineering. J.-M.G.D.N.: laser delivery quality control and improvements. A.N.: target fabrication engineering, capsule and fabrication planning. R.N.: simulations of ensembles. M.V.P.: HYDRA code development. L.J.P.: kaser delivery quality control and improvements. J.L.P.: simulations of ensembles. Y.P.: hohlraum physics. B.B.P.: hohlraum physics. M.R.: capsule fabrication. N.G.R.: capsule fabrication. H.R.: real-time neutron activation detector’s mode 1 analysis. M.R.: hohlraum physics. M.S.R.: X-ray diagnostics. J.D.S.: hohlraum physics. J.S.: mode 1 analysis. S.S.: capsules. D.J.S.: neutron diagnostics. M.B.S.: hohlraum diagnostics. C.R.S.: HYDRA code development. H.A.S.: NLTE opacities (Cretin) code development. S.M.S.: HYDRA code development. K.S.: mode 1 metrology. M.W.S.: kinetic physics. S.S.: sagometer data and particle analysis. V.A.S.: capsule physics. B.K.S.: ensemble simulations. P.T.S.: dynamic model and ignition theory. M.S.: capsules. S.S.: X-ray diagnostics. D.J.S.: hohlraum/LPI physics. L.J.S.: hohlraum physics. C.A.T.: Bigfoot design physics. R.P.J.T.: program management. C.T.: X-ray diagnostics. E.R.T.: optical diagnostics. P.L.V.: neutron imaging diagnostics. K.W.: X-ray diagnostics. C.W.: capsule fabrication. C.H.W.: neutron diagnostics. B.M.V.W.: NIF operations lead. D.T.W.: hohlraum physics. B.N.W.: project engineering. M.Y.: capsule fabrication. S.T.Y.: laser delivery quality control and improvements. G.B.Z.: computational physics lead.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Erik Lefebvre, Robbie Scott and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Radiation flux asymmetries.
Calculated normalized Legendre decompositions of the radiation flux moments (P1/P0 in blue P2/P0 in red and P4/P0 in grey) as a function of time with a dashed horizontal line at the position of zero asymmetry. The incident cone fraction (ratio of inner power to total power) and laser power profiles shown below the radiation flux asymmetries for HYBRID-E (top) and I-Raum (bottom). The total laser power as a function of time is shown before (solid) and after (dashed) drive multi- pliers are applied to the pulse to match experimental data.
Extended Data Fig. 2 Linear growth factors for high-mode perturbations.
Ablation front growth factors (AFGF) (top) and fuel-ablator interface growth factors (FAGF) (bottom) as a function of mode number at peak implosion velocity for HYBRID-E (black) and I-Raum (red), showing a tradeoff in design stability at the two interfaces due to differences in the dopant layer thickness. The shaded bands show the growth factors at ± 50 ps from peak implosion velocity.
Extended Data Fig. 3 Neutron yield amplification from alpha heating.
Calculated Yield amplification, ratio of total yield as a result of alpha particle heating to yield from simulations where the alpha particle heating is artificially turned off for HYBRID-E (red) and I-Raum (blue) as a function of total yield. Each point is a high-resolution capsule simulation which applies different combinations of the known perturbations. The lines correspond to the total measured yields from the four experiments discussed in the main text (N201101, N201122, N210207, and N210220).
Extended Data Fig. 4 Shell and hot spot configurations at peak neutron production.
Each image is 200 × 200 μm with color scale(s) normalized to the maximum value(s) in that panel. Top row: Measured fluence-compensated down-scattered neutron images (FC-DSNI) for each shot. Red indicates regions of higher areal density and neutron scatter. Center row: Simulated FC-DSNI images from 2D radiation-hydrodynamic capsule-only simulations for each shot with known degradations, including the capsule support tent and fill tube (low mode mix), surface roughness (high mode mix), x-ray drive asymmetries, and as-fabricated shell non-uniformity. Bottom row: Simulated density (left) and ion temperature (right) maps at peak neutron production. The maximum (density, ion temperature) values for each panel, left to right, in (g/cc, keV) are: (350, 7.31), (450, 6.49), (350, 8.4), (450, 7.2).
Extended Data Fig. 5 Target dimensions.
Schematics of the HYBRID-E (a) and I-Raum designs (b) showing the nominal target dimensions for the hohlraums (left) and pie charts for the central DT-fuel filled capsules (right). The HDC ablator consists of a ~ 5 μm inner un-doped HDC layer, followed by a Tungsten (W) doped HDC layer at larger radii, and an outer un-doped HDC layer. See Extended Data Table 1 for additional design parameters.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kritcher, A.L., Young, C.V., Robey, H.F. et al. Design of inertial fusion implosions reaching the burning plasma regime. Nat. Phys. 18, 251–258 (2022). https://doi.org/10.1038/s41567-021-01485-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-021-01485-9
This article is cited by
-
Isotope engineering achieved by local coordination design in Ti-Pd co-doped ZrCo-based alloys
Nature Communications (2024)
-
Demonstration of a hydrodynamically equivalent burning plasma in direct-drive inertial confinement fusion
Nature Physics (2024)
-
HB11—Understanding Hydrogen-Boron Fusion as a New Clean Energy Source
Journal of Fusion Energy (2023)
-
Generation, measurement, and modeling of strong magnetic fields generated by laser-driven micro coils
Reviews of Modern Plasma Physics (2023)
-
Evidence for suprathermal ion distribution in burning plasmas
Nature Physics (2023)