Abstract
Clonal dominance arises when the descendants (clones) of one or a few founder cells contribute disproportionally to the final structure during collective growth1,2,3,4,5,6,7,8. In contexts such as bacterial growth, tumorigenesis and stem cell reprogramming2,3,4, this phenomenon is often attributed to pre-existing propensities for dominance, whereas in stem cell homeostasis, neutral drift dynamics are invoked5,6. The mechanistic origin of clonal dominance during development, where it is increasingly documented1,6,7,8, is less understood. Here, we investigate this phenomenon in the Drosophila melanogaster follicle epithelium, a system in which the joint growth dynamics of cell lineage trees can be reconstructed. We demonstrate that clonal dominance can emerge spontaneously, in the absence of pre-existing biases, as a collective property of evolving excitable networks through coupling of divisions among connected cells. Similar mechanisms have been identified in forest fires and evolving opinion networks9,10,11; we show that the spatial coupling of excitable units explains a critical feature of the development of the organism, with implications for tissue organization and dynamics1,12,13.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Experimental data for cluster sizes in egg chambers are available at https://github.com/rozmanj/CD_ExcitableNetworks.
Code availability
All custom codes are available at https://github.com/rozmanj/CD_ExcitableNetworks.
References
Gupta, V. & Poss, K. D. Clonally dominant cardiomyocytes direct heart morphogenesis. Nature 484, 479–484 (2012).
Hall, B. A., Piterman, N., Hajnal, A. & Fisher, J. Emergent stem cell homeostasis in the C. elegans germline is revealed by hybrid modeling. Biophys. J. 109, 428–438 (2015).
Luria, S. E. & Delbrück, M. Mutations of bacteria from virus sensitivity to virus resistance. Genetics 48, 491–511 (1943).
Shakiba, N. et al. Cell competition during reprogramming gives rise to dominant clones. Science 346, eaan0925 (2019).
Lopez-Garcia, C., Klein, A. M., Simons, B. D. & Winton, D. J. Intestinal stem cell replacement follows a pattern of neutral drift. Science 330, 822–825 (2010).
Snippert, H. J. et al. Intestinal crypt homeostasis results from neutral competition between symmetrically dividing Lgr5 stem cells. Cell 143, 134–144 (2010).
Kamimoto, K. et al. Heterogeneity and stochastic growth regulation of biliary epithelial cells dictate dynamic epithelial tissue remodeling. eLife 5, e15034 (2016).
Sereti, K.-I. et al. Analysis of cardiomyocyte clonal expansion during mouse heart development and injury. Nat. Commun. 9, 754 (2018).
Mikhailov A. S. in Nonlinear Wave Processes in Excitable Media NATO ASI Series Vol. 244 (eds Holden A. V. et al.) 127–144 (Springer, 1991).
Bak, P., Chen, K. & Tang, C. A forest-fire model and some thoughts on turbulence. Phys. Lett. A 147, 297–300 (1990).
Pei, S., Tang, S. & Zheng, Z. Detecting the influence of spreading in social networks with excitable sensor networks. PLoS One 10, e0124848 (2015).
Clayton, E. et al. A single type of progenitor cell maintains normal epidermis. Nature 446, 185–189 (2007).
Imran Alsous, J., Villoutreix, P., Stoop, N., Shvartsman, S. Y. & Dunkel, J. Entropic effects in cell lineage tree packings. Nat. Phys. 14, 1016–1021 (2018).
King, R. C. Ovarian Development in Drosophila Melanogaster (Academic Press, 1970).
Margolis, J. & Spradling, A. C. Identification and behavior of epithelial stem cells in the Drosophila ovary. Development 121, 3797–3807 (1995).
King, R. C. & Vanoucek, E. G. Oogenesis in adult Drosophila melanogaster. X. Studies on the behavior of the follicle cells. Growth 24, 333–338 (1960).
Deng, W.-M., Althauser, C. & Ruohola-Baker, H. Notch-Delta signaling induces a transition from mitotic cell cycle to endocycles in Drosophila follicle cells. Development 128, 4737–4746 (2001).
Airoldi, S. J., McLean, P. F., Shimada, Y. & Cooley, L. Intercellular protein movement in syncytial Drosophila follicle cells. J. Cell Sci. 124, 4077–4086 (2011).
McLean, P. F. & Cooley, L. Protein equilibration through somatic ring canals in Drosophila. Science 340, 1445–1447 (2013).
McLean, P. F. & Cooley, L. Bridging the divide. Fly 8, 12–18 (2013).
Buckingham, M. E. & Meilhac, S. M. Tracing cells for tracking cell lineage and clonal behavior. Dev. Cell 21, 394–409 (2011).
Nystul, T. & Spradling, A. C. Regulation of epithelial stem cell replacement and follicle formation in the Drosophila ovary. Genetics 184, 503–515 (2010).
Dorfman, R. A formula for the Gini coefficient. Rev. Econ. Stat. 61, 146–149 (1979).
Xu, S., Böttcher, L. & Chou, T. Diversity in biology: definitions, quantification and models. Phys. Biol. 17, 031001 (2020).
Sutton, J. Gibrat’s legacy. J. Econ. Lit. 35, 40–59 (1997).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Sawamiphak, S., Kontarakis, Z., Filosa, A., Reischauer, S. & Stainier, D. Y. R. Transient cardiomyocyte fusion regulates cardiac development in zebrafish. Nat. Commun. 8, 1525 (2017).
Kromer, J., Khaledi-Nasab, A., Schimansky-Geier, L. & Neiman, A. B. Emergent stochastic oscillations and signal detection in tree networks of excitable elements. Sci. Rep. 7, 3956 (2017).
Tyson, J. J. Modeling the cell division cycle: cdc2 and cyclin interactions. Proc. Natl Acad. Sci. USA 88, 7328–7332 (1991).
Hochegger, H., Takeda, S. & Hunt, T. Cyclin-dependent kinases and cell-cycle transitions: does one fit all? Nat. Rev. Mol. Cell Biol. 9, 910–916 (2008).
Shcherbata, H. R., Althauser, C., Findley, S. D. & Ruohola-Baker, H. The mitotic-to-endocycle switch in Drosophila follicle cells is executed by Notch-dependent regulation of G1/S, G2/M and M/G1 cell-cycle transitions. Development 131, 3169–3181 (2004).
Drossel, B. & Schwabl, F. Self-organized critical forest-fire model. Phys. Rev. Lett. 69, 1629–1632 (1992).
Puliafito, A. et al. Collective and single cell behavior in epithelial contact inhibition. Proc. Natl Acad. Sci. USA 109, 739–744 (2012).
Datar, S. A., Jacobs, H. W., de la Cruz, A. F. A., Lehner, C. F. & Edgar, B. A. The Drosophila Cyclin D–Cdk4 complex promotes cellular growth. EMBO J. 19, 4543–4554 (2000).
Batchelor, E., Loewer, A., Mock, C. & Lahav, G. Stimulus‐dependent dynamics of p53 in single cells. Mol. Syst. Biol. 7, 488 (2011).
Roan, H.-Y., Tseng, T.-Z. & Chen, C.-H. Whole-body clonal mapping identifies giant dominant clones in zebrafish skin epidermis. Development 148, dev199669 (2021).
Wong, L. C. & Schedl, P. Dissection of Drosophila ovaries. J. Vis. Exp. 1, 52 (2006).
Imaris v.8.3.1 (Bitplane Inc., 2016).
Prasad, M., Jang, A. C.-C., Starz-Gaiano, M., Melani, M. & Montell, D. J. A protocol for culturing Drosophila melanogaster stage 9 egg chambers for live imaging. Nat. Protoc. 2, 2467–2473 (2007).
Jia, D., Xu, Q., Xie, Q., Mio, W. & Deng, W.-M. Automatic stage identification of Drosophila egg chamber based on DAPI images. Sci. Rep. 6, 18850 (2016).
Acknowledgements
We thank G. Laevsky for expert help with imaging and E. Coen for advice on how to improve the manuscript and broaden its scope. We thank E. Wieschaus, T. Schüpbach, A. Berezhkovskii, M. Krajnc, S. Dutta and C. Tarnita for helpful discussions, D. Hellwig for assistance with movie making, J. Jackson for manuscript editing and the Martin Lab (Biology, Massachusetts Institute of Technology) for lab stocks and microscopy. This work was supported by the United States National Institutes of Health (research project grant no. R01GM134204-02) (S.Y.S.) and by the Slovenian Research Agency (research core funding no. P1-0055) (J.R.).
Author information
Authors and Affiliations
Contributions
J.I.A., S.Y.S. and A.K. designed the research. J.I.A. performed the experiments and analysed the data. S.Y.S. and A.K. developed the theory. J.R. implemented and analysed all theoretical models and simulations. R.A.M. designed the flies. J.I.A., J.R. and S.Y.S. wrote the manuscript with input from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Jordi Garcia-Ojalvo, Denise Montell and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Incomplete cytokinesis leaves daughter cells connected through stable ring canals.
a, Egg chambers expressing the nuclear Proliferating Cell Nuclear Antigen (PCNA, green) and stained for Hindsight (Hnt) (magenta), which labels endocycling follicle cells that have exited mitosis17. Drosophila follicle cells increase in number through mitosis before transitioning to endocycling, during which the follicle cells duplicate their DNA without dividing; follicle cells that have exited the mitotic cell cycle are ‘post-mitotic’. The endocycle is thought to start at stage 6, a point at which the egg chambers will have started to visibly elongate17,40. Scale bar = 10 μm. b, Formation of a ring canal (arrowhead) in dividing epithelial cells in an egg chamber expressing fluorescently labeled Spaghetti squash (Sqh, green) and Pavarotti (Pav, magenta). Time in minutes; scale bar = 5 μm. c, Cross-sectional view of an epithelium with fluorescently labeled Sqh (green) and Pav (red), showing the variable positions (arrowheads) of the ring canals along the membrane (a is apical, b is basal), which necessitates acquisition and analysis of 3D images for identification of intercellular connections and cluster sizes. Scale bar = 5 μm. d, Confocal images of the surfaces of two egg chambers expressing fluorescently labeled Pav (red) and labeled with anti-E-cadherin (E-cad, blue) overlaid with reconstructed clusters: Spots of a given colour denote cells belonging to a cluster: two (white, blue) and three (green, yellow, and orange) clusters of connected cells are shown in the younger and older egg chamber, respectively. Cluster size determination and visualization were performed in Bitplane’s Imaris40. Scale bar = 10 μm. e, Box plots of the number of clusters and singles (cells unconnected to others through ring canals) in ‘stage 1’ egg chambers (n = 11); the whiskers encapsulate the entire data, the bottom and top sides of the box indicate the first and third quartile of the data, respectively, and the white line shows the median. f, Plot of the number of clusters as a function of total cell number, used to extract the probability that a division does not lead to a ring canal \(p_{{{\mathrm{c}}}} = 0.026 \pm 0.003\). Line shows a linear fit.
Extended Data Fig. 2 Comparison of diversity measures used to quantify cluster size divergence.
a, Largest cluster fraction (that is Berger-Parker index), b, Gini coefficient, c, Shannon index, d, evenness, e, Theil index, f, Simpson’s index (with replacement), and g, Hoover index for experimental egg chambers (red points), along with theoretical predictions given by the Forest Fire model simulations (grey; parameters \(p_{{{\mathrm{i}}}} = 0.0001\), \(p_{{{\mathrm{t}}}} = 0.7\), \(p_{{{\mathrm{r}}}} = 0.158114,\;p_{{{\mathrm{c}}}} = 0.026\)) averaged over 2,200 simulation runs. Grey error bars indicate the standard deviation in simulations.
Extended Data Fig. 3 Largest cluster fractions and Gini coefficients as obtained from the Independent and Cell Cycle Timer models of uncoupled cell divisions.
a, Distribution of final largest cluster sizes as fractions of all cells in the Independent model, based on 2,200 simulation runs. Dashed lines indicate the experimental values obtained by averaging over all egg chambers with >600 cells (largest cluster size fraction = 0.36, s.d. = 0.06; n = 7). b, Distribution of final Gini coefficients in the Independent model, again based on 2,200 simulation runs. Dashed lines indicate the experimental values obtained by averaging over all egg chambers with >600 cells (G = 0.81, s.d. = 0.03; n = 7; see Supplementary Table 3 for experimental data in a and b). c, Final largest cluster size as a fraction of all cells (blue) and the Gini coefficient (grey) as obtained from the Cell Cycle Timer model with the mean cell division time \(t_0 = 9.6\) h15, at different values of standard deviation \(\sigma _0\) of cell division time, averaged over 2,200 simulation runs. Error bars indicate standard deviation in simulations; dashed lines indicate experimental values averaged over all egg chambers with >600, as in a and b.
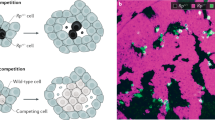
Extended Data Fig. 4 The correlated nature of epithelial cell divisions.
a, Epithelial surface of two egg chambers stained for the mitotic marker Cyclin B (CycB), showing domains (~5-15 cells) of coordinated expression. Arrowheads pointing to two adjacent dividing cells in one of those domains. b, Surface of a follicle epithelium expressing fluorescently labeled Pav (red), and the nuclear Proliferating Cell Nuclear Antigen (PCNA); arrowheads point to dividing connected cells. Scale bars in a and b = 10 μm.
Extended Data Fig. 5 Largest cluster sizes in the Forest Fire model.
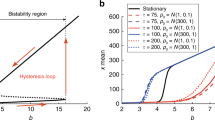
Final size fractions of the largest cluster as a function of \(p_{{{\mathrm{t}}}}\) and \(p_{{{\mathrm{r}}}}/p_{{{\mathrm{i}}}}\) for different orders of magnitude of \(p_{{{\mathrm{i}}}}\) and averaged over 2,200 simulations at each parameter set. Regardless of the value of \(p_{{{\mathrm{i}}}}\), similar average sizes occur at the same value of \(p_{{{\mathrm{t}}}}\) and a given \(p_{{{\mathrm{r}}}}/p_{{{\mathrm{i}}}}\) ratio. Cyan-bordered region indicates where experimental and theoretical values are less than an experimental standard deviation apart (experimental value average over all chambers with >600 cells: largest cluster size fraction = 0.36, s.d. = 0.06, n = 7; Supplementary Table 3).
Extended Data Fig. 6 Analysis of the Forest Fire model parameter space.
Plots of the average chi-square coefficient (\(\left< \chi ^2 \right>\); see Methods) of the diversity indices between the Forest Fire model simulations and the experimental data for all egg chambers with >61 cells, for different values of \(p_{{{\mathrm{t}}}}\) as a function of \(p_{{{\mathrm{i}}}}\) and \(p_{{{\mathrm{r}}}}\). Average chi-square coefficient values exceeding 100 are shown in white.
Extended Data Fig. 7 Comparison of the (standardized) moments of the distribution of cluster sizes.
a, Mean \(\left[ {\mu = \left< x_i \right>} \right]\), b, variance \(\left[ {\sigma ^2 = \left< \left( {x_i - \mu } \right)^2 \right>} \right]\), c, skewness \(\left[ {\tilde \mu _3 = \left< \left( {x_i - \mu } \right)^3/\sigma ^3 \right>} \right]\), and d, kurtosis \(\left[ {\tilde \mu _4 = \left< \left( {x_i - \mu } \right)^4/\sigma ^4 \right>} \right]\), where \(x_i\) is the number of cells in the \(i\)th cluster and < > indicates the average over all clusters in a chamber, for experimental egg chambers (red points) and theoretical predictions given by the Forest Fire model simulations (grey; parameters \(p_{{{\mathrm{i}}}} = 0.0001\), \(p_{{{\mathrm{t}}}} = 0.7\), \(p_{{{\mathrm{r}}}} = 0.158114,p_{{{\mathrm{c}}}} = 0.026\)), averaged over 2,200 simulation runs. Grey error bars indicate standard deviation in simulations.
Extended Data Fig. 8 Average largest cluster sizes obtained from the Independent and the Cell Cycle Timer models with differential growth.
Left panel: final size of the largest cluster as a fraction of total cell number for the Independent model with differential growth, averaged over 2,200 simulation runs, as a function of the ratio of division probability weights for the fast and slow-growing cell populations, \(w_{{{\mathrm{f}}}}/w_{{{\mathrm{s}}}}\), and the probability of each starting cluster being assigned to the fast-growing population, \(p_{{{\mathrm{f}}}}\). Cyan-bordered region in both panels shows where theoretical and experimental values of the final largest cluster fraction are less than an experimental standard deviation apart (experimental value average over all chambers with >600 cells: largest cluster size fraction = 0.36, s.d. = 0.06, n = 7; Supplementary Table 3). Right panel: final size of the largest cluster as a fraction of total cell number for the Cell Cycle Timer differential growth model for \(t_{{{\mathrm{s}}}}\) = 9.6 h and \(\sigma _{{{\mathrm{s}}}} = \sigma _{{{\mathrm{f}}}} = 0.5\) h, averaged over 2,200 simulation runs, as a function of the mean division time ratio between the fast and slow cell populations, \(t_{{{\mathrm{f}}}}/t_{{{\mathrm{s}}}}\), and the probability of each starting cluster being assigned to the fast population, \(p_{{{\mathrm{f}}}}\).
Extended Data Fig. 9 Analysis of the Cell Cycle Timer differential growth model parameter space.
Final largest cluster size as fraction of total cell number at different \(\sigma _{{{\mathrm{f}}}}\) and \(\sigma _{{{\mathrm{s}}}}\), for \(t_{{{\mathrm{s}}}}\) = 9.6 h, averaged over 2,200 simulation runs, as a function of the mean division time ration between the fast and slow cell populations, \(t_{{{\mathrm{f}}}}/t_{{{\mathrm{s}}}}\), and the probability of each starting cluster being assigned to the fast population, \(p_{{{\mathrm{f}}}}\). Cyan-bordered region indicates where experimental and theoretical values are less than an experimental standard deviation apart (experimental value average over all chambers with >600 cells: largest cluster size fraction = 0.36, s.d. = 0.06, n = 7; Supplementary Table 3).
Supplementary information
Supplementary Information
Supplementary Tables 1–3.
Supplementary Data
Experimentally determined cluster sizes for Figs. 2 and 3 and Extended Data Figs. 1–3, 5 and 6.
Supplementary Video 1
A z-stack through a fixed egg chamber (~1,000 total cells), with fluorescently labelled Pav (ring canals, red) and immunolabelled for E-cadherin (membranes, green). Scale bar, 20 μm; z-step, 0.5 μm. This type of data was acquired for reconstructing the number of clusters and their size distributions at various stages of egg chamber development.
Supplementary Video 2
A maximum intensity projection (MIP) from a four-dimensional live imaging experiment of the epithelial surface of an egg chamber expressing fluorescently tagged Jupiter (Jup), which labels the mitotic spindle of dividing cells. Blue, orange and white arrows point to groups of 2, 5 and 4 adjacent dividing follicle cells. Number of optical slices, 17; frame interval, 3 min; scale bar, 10 μm.
Supplementary Video 3
MIP from a four-dimensional live imaging experiment of an egg chamber epithelium expressing fluorescently tagged E2F1 (green) and CycB (red), showing mitotic events among adjacent follicle cells, going from left to right (white arrowheads point to dividing cells; yellow arrowheads point to daughter cells. Number of optical slices, 17; frame interval, 3 min; scale bar, 10 μm.
Supplementary Video 4
Left, animation of the growth of a simulated tissue under the Forest Fire model for parameters \(p_{{{\mathrm{i}}}} = 0.0001\), \(p_{{{\mathrm{t}}}} = 0.7\), \(p_{{{\mathrm{r}}}} = 5 \cdot 10^{ - 1.5},\;p_{{{\mathrm{c}}}} = 0.026\), starting from the 25 clusters and singles in EC1 (Supplementary Table 2). The top left cluster grows to become dominant, with its progeny containing 687 cells (red border). Due to complete divisions, cells are partitioned between several clusters, with the largest containing 334 cells. Colour coding as in Fig. 3a: green for tree, red for fire, grey for refractory. Frames show the state of the network after each division. Right, zoom in on the dominant cluster.
Supplementary Video 5
Animation illustrating the two mechanisms by which division propagation can be stopped. Both examples start with a spontaneous division of the middle cell that propagates to both of its neighbors, resulting in a cluster with six cells (colour coding as in Fig. 3a: green for tree, red for fire, grey for refractory). In the top row, propagation of divisions following the second spontaneous division is stopped stochastically, as a dividing cell will induce a division in its neighbour only with probability \(p_{{{\mathrm{t}}}}\). In the bottom row, fewer cells leave the refractory state by the time of the second spontaneous ignition (for example, due to a lower \(p_{{{\mathrm{r}}}}\)); therefore, regardless of the coupling \(p_{{{\mathrm{t}}}}\), propagation of divisions is stopped once it hits a refractory cell. Branching is not considered in this schematic.
Supplementary Video 6
Left, MIP from a four-dimensional live imaging experiment of the epithelial surface of an egg chamber expressing fluorescently tagged PCNA (nuclear, white), Res (membrane, white) and Pav (ring canals, red). Two connected cells can be seen dividing at t = 0 (pink arrowheads), as indicated by the dimming and expansion of the nuclear PCNA signal; blue arrowheads point to the resulting daughter cells. Three additional arrowheads point to directly connected cells that divide at a later time point but are not directly adjacent. Number of optical slices, 5; frame interval, 3 min; scale bar, 10 μm. Right, a tree schematic showing a partially reconstructed growing cell network. Pink arrowheads point to dividing cells, with the corresponding time in minutes indicated on each dividing node; blue arrowheads point to the resulting daughter cells. A limitation of the Forest Fire model as implemented here is that divisions can only propagate between connected cells that are adjacent, whereas in vivo, dividing cells can be seen separated by non-dividing cells.
Rights and permissions
About this article
Cite this article
Imran Alsous, J., Rozman, J., Marmion, R.A. et al. Clonal dominance in excitable cell networks. Nat. Phys. 17, 1391–1395 (2021). https://doi.org/10.1038/s41567-021-01383-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-021-01383-0