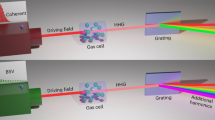
Abstract
The physics of intense laser–matter interactions1,2 is described by treating the light pulses classically, anticipating no need to access optical measurements beyond the classical limit. However, the quantum nature of the electromagnetic fields is always present3. Here we demonstrate that intense laser–atom interactions may lead to the generation of highly non-classical light states. This was achieved by using the process of high-harmonic generation in atoms4,5, in which the photons of a driving laser pulse of infrared frequency are upconverted into photons of higher frequencies in the extreme ultraviolet spectral range. The quantum state of the fundamental mode after the interaction, when conditioned on the high-harmonic generation, is a so-called Schrödinger cat state, which corresponds to a superposition of two distinct coherent states: the initial state of the laser and the coherent state reduced in amplitude that results from the interaction with atoms. The results open the path for investigations towards the control of the non-classical states, exploiting conditioning approaches on physical processes relevant to high-harmonic generation.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper. All other data that support the plots within this paper are available from the corresponding authors on reasonable request.
Code availability
The codes used in this study are available from the corresponding authors upon request.
References
Mourou, G. Nobel Lecture: Extreme light physics and application. Rev. Mod. Phys. 91, 030501 (2019).
Strickland, D. Nobel Lecture: Generating high-intensity ultrashort optical pulses. Rev. Mod. Phys. 91, 030502 (2019).
Glauber, R. J. Nobel Lecture: One hundred years of light quanta. Rev. Mod. Phys. 78, 1267–1278 (2006).
McPherson, A. et al. Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases. J. Opt. Soc. Am. B 4, 595–601 (1987).
Ferray, M. et al. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B 21, L31–L35 (1988).
Maiman, T. H. Stimulated optical radiation in ruby. Nature 187, 493–494 (1960).
Amini, K. et al. Symphony on strong field approximation. Rep. Prog. Phys. 82, 116001 (2019).
Delone, N. B. & Krainov, V. P. Multiphoton Processes in Atoms 2nd edn (Springer Series on Atomic, Optical, and Plasma Physics, Springer-Verlag, 2000).
Protopapas, M., Keitel, C. H. & Knight, P. L. Atomic physics with super-high intense lasers. Rep. Prog. Phys. 60, 389–486 (1997).
Corkum, P. B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 71, 1994–1997 (1993).
Kulander, K. C., Schafer, K. J. & Krause, J. L. in Super-Intense Laser Atom Physics (eds Piraux, B. et al.) 95–110 (NATO ASI Series B: Physics, Vol. 316, Plenum, 1993).
Lewenstein, M. et al. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 49, 2117–2132 (1994).
Leonhardt, U. in Measuring the Quantum State of Light 1st edn (eds Knight, P. L. & Miller, A.) 98–143 (Cambridge Studies in Modern Optics, Cambridge Univ. Press, 1997).
Ourjoumtsev, A., Jeong, H., Tualle-Brouri, R. & Grangier, P. Generation of optical ‘Schrödinger cats’ from photon number states. Nature 448, 784–786 (2007).
Zavatta, A., Viciani, S. & Bellini, M. Quantum-to-classical transition with single-photon-added coherent states of light. Science 306, 660–662 (2004).
Ourjoumtsev, A., Tualle-Brouri, R., Laurat, J. & Grangier, P. Generating optical Schrödinger kittens for quantum information processing. Science 312, 83–86 (2006).
Wakui, K., Takahashi, H., Furusawa, A. & Sasaki, M. Photon subtracted squeezed states generated with periodically poled KTiOPO4. Opt. Express 15, 3568–3574 (2007).
Acín, A. et al. The quantum technologies roadmap: a European community view. New J. Phys. 20, 080201 (2018).
Walmsley, I. A. Quantum optics: science and technology in a new light. Science 348, 525–530 (2015).
Deutsch, I. H. Harnessing the power of the second quantum revolution. PRX Quantum 1, 020101 (2020).
Diestler, D. J. Harmonic generation: quantum-electrodynamical theory of the harmonic photon-number spectrum. Phys. Rev. A 78, 033814 (2008).
Gonoskov, I. A., Tsatrafyllis, N., Kominis, I. K. & Tzallas, P. Quantum optical signatures in strong-field laser physics: infrared photon counting in high-order harmonic generation. Sci. Rep. 6, 32821 (2016).
Gombkötő, Á., Varró, S., Mati, P. & Földi, P. High-order harmonic generation as induced by a quantized field: phase-space picture. Phys. Rev. A 101, 013418 (2020).
Gorlach, A., Neufeld, O., Rivera, N., Cohen, O. & Kaminer, I. The quantum-optical nature of high harmonic generation. Nat. Commun. 11, 4598 (2020).
Yangaliev, D. N., Krainov, V. P. & Tolstikhin, O. I. Quantum theory of radiation by nonstationary systems with application to high-order harmonic generation. Phys. Rev. A 101, 013410 (2020).
Tsatrafyllis, N., Kominis, I. K., Gonoskov, I. A. & Tzallas, P. High-order harmonics measured by the photon statistics of the infrared driving-field exiting the atomic medium. Nat. Commun. 8, 15170 (2017).
Tsatrafyllis, N. et al. Quantum optical signatures in a strong laser pulse after interaction with semiconductors. Phys. Rev. Lett. 122, 193602 (2019).
Lvovsky, A. I. & Raymer, M. G. Continuous-variable optical quantum-state tomography. Rev. Mod. Phys. 81, 299–332 (2009).
Schleich, W. P. Quantum Optics in Phase Space (Wiley-VHC Verlag, 2001).
Breitenbach, G., Schiller, S. & Mlynek, J. Measurement of the quantum states of squeezed light. Nature 387, 471–475 (1997).
Krausz, F. & Ivanov, M. Y. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Nayak, A. et al. Saddle point approaches in strong field physics and generation of attosecond pulses. Phys. Rep. 833, 1–52 (2019).
Wünsche, A. Quantization of Gauss-Hermite and Gauss-Laguerre beams in free space. J. Opt. B 6, S47–S59 (2004).
Grynberg, G., Aspect, A. & Fabre, C. Introduction to Quantum Optics (Cambridge Univ. Press, 2010).
Acknowledgements
We dedicate this work to the memory of Roy J. Glauber, the inventor of coherent states, also a wonderful mentor. We thank J. Biegert, I. Kaminer and P. Salières for enlightening discussions. We also thank I. Liontos, E. Skantzakis and S. Karsch from Max Plank Institute for Quantum Optics for their assistance on maintaining the performance of the Ti:Sa laser system and N. Pappadakis for his contribution on the development of the data acquisition and data analysis system. M.L. group acknowledges the European Research Council (ERC AdG) NOQIA, Spanish Ministry MINECO and State Research Agency AEI (FIDEUA PID2019-106901GB-I00/10.13039/501100011033, SEVERO OCHOA No. SEV-2015-0522 and CEX2019-000910-S, FPI), European Social Fund, Fundació Cellex, Fundació Mir-Puig, Generalitat de Catalunya (AGAUR grant no. 2017 SGR 1341, CERCA programme, QuantumCAT_U16-011424, co-funded by ERDF Operational Program of Catalonia 2014-2020), MINECO-EU QUANTERA MAQS (funded by State Research Agency (AEI) PCI2019-111828-2/10.13039/501100011033), EU Horizon 2020 FET-OPEN OPTOLogic (grant no. 899794), and the National Science Centre, Poland-Symfonia grant no. 2016/20/W/ST4/00314. M.F.C. acknowledges the Grantová agentura Ceské Republiky (GACR grant 20-24805J). J.R.-D. has received funding from the Secretaria d’Universitats i Recerca del Departament d’Empresa i Coneixement de la Generalitat de Catalunya, as well as the European Social Fund (L’FSE inverteix en el teu futur)–FEDER. P.T. group acknowledges LASERLABEUROPE (H2020-EU.1.4.1.2 grant ID 654148), FORTH Synergy Grant AgiIDA (grant no. 00133), the European Union’s Horizon 2020 framework programme for research and innovation under the NFFA-Europe-Pilot project (grant no. 101007417), the HELLAS-CH (MIS grant no. 5002735) (which is implemented under the Action for Strengthening Research and Innovation Infrastructures, funded by the Operational Program Competitiveness, Entrepreneurship and Innovation (NSRF 2014-2020) and co-financed by Greece and the European Union (European Regional Development Fund)), and the European Union’s Horizon 2020 research. ELI-ALPS is supported by the European Union and co-financed by the European Regional Development Fund (GINOP grant no. 2.3.6-15-2015-00001).
Author information
Authors and Affiliations
Contributions
M.L. supervised the theoretical part of the work; M.F.C., J.R.-D. and E.P. equally contributed to the manuscript preparation and the development of the theoretical approach; P.S. contributed to the theoretical calculations; Th.L. contributed in the experimental runs and data analysis; P.T. supervised the experimental part of the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Discussion and Figs. 1–3.
Source data
Source Data Fig. 2
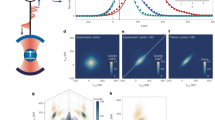
Calculated Wigner function of the optical kitten (Fig. 2a,b) and cat (Fig. 2c,d) states.
Source Data Fig. 3
Measured Wigner function of the laser coherent state (Fig. 3b).
Source Data Fig. 4
Measured Wigner function of the cat state.
Rights and permissions
About this article
Cite this article
Lewenstein, M., Ciappina, M.F., Pisanty, E. et al. Generation of optical Schrödinger cat states in intense laser–matter interactions. Nat. Phys. 17, 1104–1108 (2021). https://doi.org/10.1038/s41567-021-01317-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-021-01317-w
This article is cited by
-
Multiphoton electron emission with non-classical light
Nature Physics (2024)
-
Motion of charged particles in bright squeezed vacuum
Light: Science & Applications (2024)
-
Light emission from strongly driven many-body systems
Nature Physics (2023)
-
Dynamical entropic measure of nonclassicality of phase-dependent family of Schrödinger cat states
Scientific Reports (2023)
-
Photon-statistics force in ultrafast electron dynamics
Nature Photonics (2023)