Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Mirror symmetry breaking in a model insulating cuprate

Nature Physics volume 17, pages 777–781 (2021)Cite this article

Subjects

Abstract

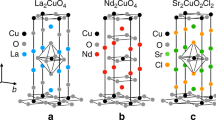
Among the most actively studied issues in the cuprates are the natures of the pseudogap and strange metal states and their relationship to superconductivity1. There is general agreement that the low-energy physics of the Mott-insulating parent state is well captured by a two-dimensional spin S = 1/2 antiferromagnetic Heisenberg model2. However, recent observations of a large thermal Hall conductivity in several parent cuprates appear to defy this simple model and suggest proximity to a magneto-chiral state that breaks all mirror planes that are perpendicular to the CuO2 layers3,4,5,6. Here we use optical second harmonic generation to directly resolve the point group symmetries of the model parent cuprate Sr2CuO2Cl2. We report evidence of an order parameter that breaks all perpendicular mirror planes and is consistent with a magneto-chiral state in zero magnetic field. Although this order is clearly coupled to the antiferromagnetism, we are unable to realize its time-reversed partner by thermal cycling through the antiferromagnetic transition temperature or by sampling different spatial locations. This suggests that the order onsets above the Néel temperature and may be relevant to the mechanism of pseudogap formation.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: SHG from Sr2CuO2Cl2.
Fig. 2: Mirror symmetry breaking in the AFM state.
Fig. 3: Temperature dependence of the SHG response.
Fig. 4: Order parameter symmetry and spatial dependence.

Similar content being viewed by others

Data availability

Source data are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

References

  1. Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).

    ADS  Google Scholar 

  2. Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).

    Article  ADS  Google Scholar 

  3. Grissonnanche, G. et al. Giant thermal Hall conductivity in the pseudogap phase of cuprate superconductors. Nature 571, 376–380 (2019).

    Article  ADS  Google Scholar 

  4. Boulanger, Marie-Eve et al. Thermal Hall conductivity in the cuprate Mott insulators Nd2CuO4 and Sr2CuO2Cl2. Nat. Commun. 11, 5325 (2020).

    Article  ADS  Google Scholar 

  5. Han, J. H., Park, J.-H. & Lee, P. A. Consideration of thermal Hall effect in undoped cuprates. Phys. Rev. B 99, 205157 (2019).

    Article  ADS  Google Scholar 

  6. Samajdar, R., Chatterjee, S., Sachdev, S. & Scheurer, M. S. Thermal Hall effect in square-lattice spin liquids: a Schwinger boson mean-field study. Phys. Rev. B 99, 165126 (2019).

    Article  ADS  Google Scholar 

  7. Grande, B. & Müller-Buschbaum, H. über erdalkalimetalloxocuprate, VIII Zur Kenntnis von Sr2CuO2Cl2. Z. Anorg. Allg. Chem. 417, 68–74 (1975).

    Article  Google Scholar 

  8. Miller, L. L. et al. Synthesis, structure, and properties of Sr2CuO2Cl2. Phys. Rev. B 41, 1921–1925 (1990).

    Article  ADS  Google Scholar 

  9. Cuccoli, A., Roscilde, T., Vaia, R. & Verrucchi, P. Detection of XY behavior in weakly anisotropic quantum antiferromagnets on the square lattice. Phys. Rev. Lett. 90, 167205 (2003).

    Article  ADS  Google Scholar 

  10. Suh, B. J. et al. Evidence for crossover effects in the spin dynamics of the two dimensional antiferromagnet Sr2CuO2Cl2 from 35Cl nuclear magnetic resonance. J. Appl. Phys. 79, 5084–5086 (1996).

    Article  ADS  Google Scholar 

  11. Katsumata, K. et al. Direct observation of the quantum energy gap in S = 1/2 tetragonal cuprate antiferromagnets. Europhys. Lett. 54, 508–514 (2001).

    Article  ADS  Google Scholar 

  12. Greven, M. et al. Neutron scattering study of the two-dimensional spin S = 1/2 square-lattice Heisenberg antiferromagnet Sr2CuO2Cl2. Z. Phys. B 96, 465–477 (1995).

    Article  ADS  Google Scholar 

  13. Fiebig, M., Pavlov, V. V. & Pisarev, R. V. Second-harmonic generation as a tool for studying electronic and magnetic structures of crystals: review. J. Opt. Soc. Am. B 22, 96–118 (2005).

    Article  ADS  Google Scholar 

  14. Harter, J. W., Niu, L., Woss, A. J. & Hsieh, D. High-speed measurement of rotational anisotropy nonlinear optical harmonic generation using position-sensitive detection. Opt. Lett. 40, 4671–4674 (2015).

    Article  ADS  Google Scholar 

  15. Choi, H. S. et al. Anomalous temperature dependence of charge-transfer excitation in the undoped cuprate Sr2CuO2Cl2. Phys. Rev. B 60, 4646–4652 (1999).

    Article  ADS  Google Scholar 

  16. Vaknin, D., Sinha, S. K., Stassis, C., Miller, L. L. & Johnston, D. C. Antiferromagnetism in Sr2CuO2Cl2. Phys. Rev. B 41, 1926–1933 (1990).

    Article  ADS  Google Scholar 

  17. Ye, F. et al. Structure symmetry determination and magnetic evolution in Sr2Ir1−xRhxO4. Phys. Rev. B 92, 201112(R) (2015).

    Article  ADS  Google Scholar 

  18. Farzaneh, M., Liu, X. F., El-Batanouny, M. & Chou, F. C. Structure and lattice dynamics of Sr2CuO2Cl2(001) studied by helium-atom scattering. Phys. Rev. B 72, 085409 (2005).

    Article  ADS  Google Scholar 

  19. Dürr, C. et al. Angle-resolved photoemission spectroscopy of Sr2CuO2Cl2. Phys. Rev. B 63, 014505 (2000).

    Article  ADS  Google Scholar 

  20. Ron, A., Zoghlin, E., Balents, L., Wilson, S. D. & Hsieh, D. Dimensional crossover in a layered ferromagnet detected by spin correlation driven distortions. Nat. Commun. 10, 1654 (2019).

    Article  ADS  Google Scholar 

  21. De Luca, G. M. et al. Weak magnetism in insulating and superconducting cuprates. Phys. Rev. B 82, 214504 (2010).

    Article  ADS  Google Scholar 

  22. Fiebig, M., Fröhlich, D., Sluyterman, v. L. G. & Pisarev, R. V. Domain topography of antiferromagnetic Cr2O3 by second harmonic generation. Appl. Phys. Lett. 66, 2906–2908 (1995).

    Article  ADS  Google Scholar 

  23. Fechner, M., Fierz, M. J. A., Thöle, F., Staub, U. & Spaldin, N. A. Quasistatic magnetoelectric multipoles as order parameter for pseudogap phase in cuprate superconductors. Phys. Rev. B 93, 174419 (2016).

    Article  ADS  Google Scholar 

  24. Varma, C. Non-Fermi-liquid states and pairing instability of a general model of copper oxide metals. Phys. Rev. B 55, 14554–14580 (1997).

    Article  ADS  Google Scholar 

  25. Aji, V., Shekhter, A. & Varma, C. M. Theory of the coupling of quantum-critical fluctuations to fermions and d-wave superconductivity in cuprates. Phys. Rev. B 81, 064515 (2010).

    Article  ADS  Google Scholar 

  26. He, Y., Lee, P. A. & Varma, C. M. Intrinsic anomalous Hall effect in magnetochiral states. Phys. Rev. B 89, 035119 (2014).

    Article  ADS  Google Scholar 

  27. Scheurer, M. S. & Sachdev, S. Orbital currents in insulating and doped antiferromagnets. Phys. Rev. B 98, 235126 (2018).

    Article  ADS  Google Scholar 

  28. Sachdev, S. Colloquium: order and quantum phase transitions in the cuprate superconductors. Rev. Mod. Phys. 75, 913–932 (2003).

    Article  ADS  Google Scholar 

  29. Dai, Z., Senthil, T. & Lee, P. A. Modeling the pseudogap metallic state in cuprates: quantum disordered pair density wave. Phys. Rev. B 101, 064502 (2020).

    Article  ADS  Google Scholar 

  30. Wang, X. L. et al. Antiferromagnetic form factor of Sr2CuO2Cl2. J. Appl. Phys. 67, 4524–4526 (1990).

    Article  ADS  Google Scholar 

  31. Guarise, M. et al. Measurement of magnetic excitations in the two-dimensional antiferromagnetic Sr2CuO2Cl2 insulator using resonant X-ray scattering: evidence for extended interactions. Phys. Rev. Lett. 105, 157006 (2010).

    Article  ADS  Google Scholar 

  32. Plumb, K. W., Savici, A. T., Granroth, G. E., Chou, F. C. & Kim, Y.-J. High-energy continuum of magnetic excitations in the two-dimensional quantum antiferromagnet Sr2CuO2Cl2. Phys. Rev. B 89, 180410 (2014).

    Article  ADS  Google Scholar 

  33. Seemann, M., Ködderitzsch, D., Wimmer, S. & Ebert, H. Symmetry-imposed shape of linear response tensors. Phys. Rev. B 92, 155138 (2015).

    Article  ADS  Google Scholar 

  34. Lubashevsky, Y., Pan, L., Kirzhner, T., Koren, G. & Armitage, N. P. Optical birefringence and dichroism of cuprate superconductors in the THz regime. Phys. Rev. Lett. 112, 147001 (2014).

    Article  ADS  Google Scholar 

  35. Zhao, L. et al. A global inversion-symmetry-broken phase inside the pseudogap region of YBa2Cu3Oy. Nat. Phys. 13, 250–254 (2017).

    Article  Google Scholar 

  36. Mukherjee, A. et al. Linear dichroism infrared resonance in overdoped, underdoped, and optimally doped cuprate superconductors. Phys. Rev. B 102, 054520 (2020).

    Article  ADS  Google Scholar 

  37. Fauqué, B. et al. Magnetic order in the pseudogap phase of high-TC superconductors. Phys. Rev. Lett. 96, 197001 (2006).

    Article  ADS  Google Scholar 

  38. Tang, Y. et al. Orientation of the intra-unit-cell magnetic moment in the high-Tc superconductor HgBa2Cuo4+δ. Phys. Rev. B 98, 214418 (2018).

    Article  ADS  Google Scholar 

  39. Xia, J. et al. Polar Kerr-effect measurements of the high-temperature YBa2Cu3O6+x superconductor: evidence for broken symmetry near the pseudogap temperature. Phys. Rev. Lett. 100, 127002 (2008).

    Article  ADS  Google Scholar 

  40. Perkins, J. D. et al. Mid-infrared optical absorption in undoped lamellar copper oxides. Phys. Rev. Lett. 71, 1621–1624 (1993).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We acknowledge helpful conversations with D. Kennes, S. Kivelson, P. Lee, O. Motrunich, D. Pelc and K. Plumb. We also thank L. Taillefer and G. Grissonnanche for sharing unpublished data. The SHG work is supported by an ARO PECASE award W911NF-17-1-0204. D.H. also acknowledges support for instrumentation from the David and Lucile Packard Foundation and from the Institute for Quantum Information and Matter (IQIM), an NSF Physics Frontiers Center (PHY-1733907). A.d.l.T. acknowledges support from the Swiss National Science Foundation through an Early Postdoc Mobility Fellowship (P2GEP2_165044). K.L.S. acknowledges a Caltech Prize Postdoctoral Fellowship. S.S. acknowledges support from NSF grant DMR-2002850. M.S.S. acknowledges support from the German National Academy of Sciences Leopoldina through Grant LPDS 2016-12. M.R.N. was supported by the Materials Sciences and Engineering Division, Basic Energy Sciences, Office of Science, US Department of Energy. The work at the University of Minnesota was funded by the US Department of Energy through the University of Minnesota Center for Quantum Materials, under grant no. DE-SC-0016371.

Author information

Authors and Affiliations

  1. Department of Physics, California Institute of Technology, Pasadena, CA, USA

    A. de la Torre, K. L. Seyler & D. Hsieh

  2. Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, CA, USA

    A. de la Torre, K. L. Seyler & D. Hsieh

  3. Department of Physics, University of Michigan, Ann Arbor, MI, USA

    L. Zhao

  4. Institut de Physique de Rennes CNRS UMR 6251, Université de Rennes, Rennes, France

    S. Di Matteo

  5. Department of Physics, Harvard University, Cambridge, MA, USA

    M. S. Scheurer & S. Sachdev

  6. Institute for Theoretical Physics, University of Innsbruck, Innsbruck, Austria

    M. S. Scheurer

  7. School of Physics and Astronomy, University of Minnesota, Minneapolis, MN, USA

    Y. Li, B. Yu & M. Greven

  8. Materials Science Division, Argonne National Laboratory, Argonne, IL, USA

    M. R. Norman

Authors
  1. A. de la Torre
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. L. Seyler
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. L. Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. S. Di Matteo
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. M. S. Scheurer
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Y. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. B. Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. M. Greven
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. S. Sachdev
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. M. R. Norman
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. D. Hsieh
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.d.l.T., L.Z., D.H. and M.G. conceived the experiment. A.d.l.T., K.L.S. and L.Z. performed the optical measurements. Y.L. and B.Y. synthesized, characterized and aligned the samples. A.d.l.T., L.Z. and D.H. analysed the data. S.D.M., M.S.S., S.S. and M.R.N. performed the theoretical calculations and, together with A.d.l.T. and D.H., interpreted the results. A.d.l.T. and D.H. wrote the manuscript with input from all authors.

Corresponding author

Correspondence to D. Hsieh.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Nature Physics thanks Manfred Fiebig and Marco Grioni for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–9 and Sections 1–12.

Source data

Source Data Fig. 2

RA-SHG data.

Source Data Fig. 3

Single angle temperature dependence data.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Torre, A.d.l., Seyler, K.L., Zhao, L. et al. Mirror symmetry breaking in a model insulating cuprate. Nat. Phys. 17, 777–781 (2021). https://doi.org/10.1038/s41567-021-01210-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-021-01210-6

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing