Abstract
Effective control of an epidemic relies on the rapid discovery and isolation of infected individuals. Because many infectious diseases spread through interaction, contact tracing is widely used to facilitate case discovery and control. However, what determines the efficacy of contact tracing has not been fully understood. Here we reveal that, compared with ‘forward’ tracing (tracing to whom disease spreads), ‘backward’ tracing (tracing from whom disease spreads) is profoundly more effective. The effectiveness of backward tracing is due to simple but overlooked biases arising from the heterogeneity in contacts. We argue that, even if the directionality of infection is unknown, it is possible to perform backward-aiming contact tracing. Using simulations on both synthetic and high-resolution empirical contact datasets, we show that strategically executed contact tracing can prevent a substantial fraction of transmissions with a higher efficiency—in terms of prevented cases per isolation—than case isolation alone. Our results call for a revision of current contact-tracing strategies so that they leverage all forms of bias. It is particularly crucial that we incorporate backward and deep tracing in a digital context while adhering to the privacy-preserving requirements of these new platforms.
Similar content being viewed by others
Main
Mass quarantine has shown its effectiveness in controlling the epidemic outbreak during the coronavirus disease-2019 (COVID-19) pandemic, but with a considerable social and economic cost1,2. Once the initial outbreak has been suppressed, it is critical to manage resurgence to avoid uncontrolled spreading and another lockdown. Because voluntary testing and case isolation suffer from inevitable undetected transmissions, contact tracing is a potent intervention measure that allows the discovery and subsequent isolation of pre-symptomatic and asymptomatic cases, and plays a critical role for the successful control of emerging disease3,4,5,6,7,8,9. However, because traditional contact tracing is labour intensive and slow, its efficacy and cost–benefit trade-offs have been questioned10,11. Therefore, digital contact tracing that leverages mobile devices may allow more swift and efficient contact tracing, potentially overcoming the limitations of traditional contact tracing9.
Regardless of whether it is performed in person or digitally, contact tracing, in practice, often discovers super-spreading events, which are abundant in many epidemics12. A famous example from the COVID-19 pandemic would be the ‘Shincheonji Church’ incident associated with ‘Patient 31’ in South Korea13. This patient was the first identified positive case from the church event, which was later identified—via contact tracing—to be the single biggest super-spreading event in South Korea. This single super-spreading event eventually caused more than 5,000 cases, accounting for more than half of the total cases in South Korea during that time13. As illustrated for this case, super-spreading events are the norm rather than the exception12, and these events are often discovered through contact-tracing efforts5,14.
The ability of contact tracing to detect super-spreading events can be attributed, in part, to the ‘friendship paradox’15. The friendship paradox states that your friends tend to have more friends than you, because the more friends someone has, the more often they show up in someone’s friend list. Now, because a disease is transmitted through contact ties, the disease preferentially reaches individuals with many contacts, who can potentially cause super-spreading events. Beyond being an interesting piece of trivia, this insight has proven useful for epidemic surveillance and control16. Individuals with many social contacts, such as celebrities and politicians, are in many ways ideal sentinel nodes for epidemic outbreaks12,16,17,18.
In this Article, we argue that contact tracing is assisted by an additional statistical bias in social networks. This bias is leveraged when the contact tracing is executed backward to identify the source of infection (parent). This is because the more offspring (infections) a parent has produced, the more frequently the parent shows up as a contact. Both biases can be at play at the same time, and thus their effects are additive, resulting in an exceptional efficacy of backward contact tracing at identifying super-spreaders and super-spreading events. Although the effectiveness of backward tracing has been explored in the literature8,19,20,21,22,23,24,25, for instance by using agent-based simulations8,22 or branching process models20,21,23,24,25, a clear connection between the effectiveness and the nature of statistical biases regarding contact network structure has not yet been established.
A leading factor that determines the strengths of these statistical biases is the structural properties of the underlying contact network itself, in particular the heterogeneity of the degree (that is, the number of contacts). Heterogeneous networks, where the number of contacts varies substantially among individuals, have a larger variance in the degree, which in turn produces a stronger friendship paradox effect. Real networks are known to be heterogeneous26,27,28, with strong implications for epidemiology because these properties alter the fundamental nature of the epidemic dynamics in the form of, for example, vanishing epidemic threshold29, hierarchical spreading30, and large variance in an individual’s reproductive number12, as well as the final outbreak size31.
Here, we analyse the statistical biases that backward contact tracing leverages. Using simulations on both synthetic and empirical contact network data, we show that strategically executed contact tracing can be highly effective and efficient at controlling epidemics. Our results call not only for the incorporation of contact tracing as a more crucial part of the epidemic control strategy, but, crucially, for the implementation of backward-facing contact-tracing protocols both in traditional and digital contact-tracing programmes to fully leverage the biases afforded by empirical network structures.
Bias due to the friendship paradox
Face-to-face contacts between people can be represented as a network, where a node is a person and an edge indicates a contact between two persons. When a node in the network is infectious, the disease can be transmitted to neighbours through the edges (Fig. 1a). A node with many edges is likely to be one of the neighbours and thus has a high chance of infection. This is the friendship paradox described above15. In other words, ‘you’ are a random node having k contacts drawn from a distribution pk, whereas ‘your friends’ are those having \(k^{\prime}\) contacts drawn proportionally to \(k^{\prime} {p}_{k^{\prime} }\). The friendship paradox aggravates epidemic outbreaks because individuals with many contacts are preferentially infected and spread the infection to many others29,30,32.
a, A transmission event occurs from a ‘parent’ to a ‘focal node’ (or an offspring). b, The disease spreads from an infected node to its neighbours through edges in networks. c, The spread of disease can be represented as a transmission tree with directed edges from parents to offspring. d, Backward tracing is likely to sample parents with many offspring; for example, node 11 is more likely to be sampled than node 10 by backward tracing. e, Contact tracing can also be conducted for a bipartite network of people and gatherings. As for the contact network, a high-degree gathering is more likely to be ‘infected’ and to be traced with the same logic.
Formally, if we sample a node at random, the distribution of degree (that is, the number of contacts) is given by {pk}, which can be expressed as a probability generating function (PGF), that is
where x is a counting variable for degrees. The PGF is a polynomial representation of the degree distribution. For example, the average degree can be calculated using a derivative \(\langle k\rangle ={\sum }_{k}k{p}_{k}={G}_{0}^{\prime}(1)\). Now, consider that a node is infected and the disease is transmitted through an edge chosen at random. The disease is then k times more likely to reach a node with degree k than a node with degree 1. Therefore, the number of other contacts (that is, excess degree, k − 1) found at the end of that contact is generated by
where 〈k〉 is a normalization constant. Note that the average excess degree is larger than or equal to the average degree, \({G}_{1}^{\prime}(1)\ge {G}_{0}^{\prime}(1)\) (the friendship paradox).
This property can be leveraged by the so-called ‘acquaintance sampling’ strategy, where one randomly samples individuals and then samples their ‘friends’ by following contacts16,17. Because the acquaintance sampling can preferentially sample hubs in a network, even without knowing its whole structure, it has been shown to help early detection of an outbreak as well as efficient control of the disease16,17.
Bias due to backward tracing
An often overlooked fact about contact tracing is that there are two directions in which the contact tracing can lead to the discovery of infected individuals. The first is following the direction of the transmission—to whom the transmission may have occurred—and the other is reaching to the parent—from whom the transmission occurred. The difference has a profound implication on the statistical nature of the sampling.
Disease spreading can be represented as a tree composed of edges from parents to offspring (Fig. 1c). If we follow the transmission edge to the offspring of a node, we are sampling with the bias due to the friendship paradox (~kpk). However, when we trace back to the parent, another statistical bias comes into play. Imagine someone who has spread the disease to k individuals (for example, node 11 in Fig. 1d) and another infected individual who only spreads the disease to one individual (node 10). If we sample infected individuals (one of nodes 12–15) and follow a transmission edge back to the parent, we are likely to reach the one who has more offspring (node 11). Formally, if we trace back to the parent, the number of other offspring from the parent is generated by
The contact tracing samples a parent having k − 2 degree (that is, the number of other offspring) with a probability proportional to k(k − 1)pk (~k2pk)—a bias stronger than acquaintance sampling (~kpk). To illustrate this in practice, we simulate the ‘susceptible–exposed–infectious–recovered’ (SEIR)11 model on a degree heterogeneous network generated by the Barabási–Albert (BA) model33 (the parameters of the SEIR model are described in Methods). At an early stage (time t = 10), the degree distribution for all infected nodes and that for parents closely follow distributions proportional to kpk and k(k − 1)pk, respectively (Fig. 2a).
a,b, We simulate the SEIR model on a BA network composed of 250,000 nodes. We sample the infected nodes with probability 0.1 and trace their parents at time t = 10. In a, the blue and orange lines respectively indicate the complementary cumulative distribution function (CCDF) for the degree of the sampled nodes and their parents, which follow G1 and G2, respectively. Frequency-based contact tracing (b)—isolating the most frequently traced nodes—can reach nodes with a degree similar to the parents without knowing who infects whom. c,d, As for the contact network, both backward (c) and frequency-based (d) contact tracing can reach large degree nodes for people-gathering networks. e, The bias due to backward tracing is present even in a relatively homogeneous network. We simulate the SEIR model on a temporal contact network of university students and sample all infected nodes and their parents. The infected and parent nodes have degree distributions that closely follow G1 and G2 for the unweighted aggregated network, respectively. f, As for the contact and people-gathering networks, frequency-based contact tracing is effective at reaching large degree nodes.
Backward tracing needs information about the direction from which the infection occurs. However, except for a few diseases34, the direction of transmission is not clear in practice. Still, we can preferentially sample super-spreading parents (events) by leveraging the bias due to backward tracing. Because a super-spreader or super-spreading event infects many individuals, they would appear as a common contact or visited location of many infected individuals. For example, in Fig. 1d, node 11 is a common neighbour for three infected nodes and hence would appear three times more frequently than node 10. The bias can be leveraged by the frequency-based contact tracing, where we trace and isolate the most frequent nodes in the contact list. For the BA network, the frequency-based contact tracing samples nodes with a degree similar to the parents without knowing the direction of transmissions (Fig. 2b).
Effectiveness of contact tracing for heterogeneous networks
The backward tracing leverages the two sampling biases attributed to the heterogeneity in the degree distributions. Therefore, we hypothesize that contact tracing is highly effective in degree heterogeneous networks. As a proof of concept, we simulated epidemic spreading using the SEIR model on a network with a power-law degree distribution. The network is generated by the BA model33 and is composed of 250,000 nodes with minimum degree 2 (see ‘Simulating epidemic spreading’ in Methods for parameter values). Although the SEIR model simulated on a BA network in many respects differs from epidemic spreading in empirical social networks11,35,36, it demonstrates that contact tracing can leverage the sampling biases arising from the heterogeneity.
We intervene in epidemic spreading from time t = 0.5 by detecting and isolating newly infected individuals at the time of infection with probability ps (that is, probability of detecting infection). Then, from each detected individual, we add each contact (that is, neighbour) to a contact list with probability pt (that is, probability of successful tracing). At every interval Δt = 1, we isolate the most frequent n nodes in the contact list and then clear the list. Note that contact tracing with pt = 0 is equivalent to case isolation; that is, we discover and isolate newly infected nodes with probability ps, but do not trace close contacts. We model the contact tracing as preventing infections to all nodes rooted from the isolated nodes in the transmission tree.
The disease infects ~25% of nodes at the peak of infection (Fig. 3a). The peak can be reduced by more than 75% with contact tracing for pt ≥ 0.5 (Fig. 3a). Implementing even a small number of extra isolations through contact tracing (for example, n = 10 from the population of 250,000) is still effective in flattening the curve of infections (Fig. 3b). The effectiveness is more pronounced when we can identify more infected nodes, for example, by increasing the amount of testing (Fig. 3c).
a–l, People contact networks (a–f) and people-gathering networks (g–l) are generated by the BA and the configuration model, respectively. Contact tracing (a) lowers the peak of infection by more than 70% of that for case isolation. The effectiveness (b) stands out even if we can trace a few nodes. The efficacy of contact tracing (c) is substantially enhanced when the detection probability is increased. Compared with case isolation (pt = 0), contact tracing (pt > 0) isolates fewer nodes (d) while preventing more cases (e,f). Contact tracing is therefore highly cost-efficient in terms of the number of prevented cases per isolation. The plots in g–l correspond to those in a–f, but for people-gathering networks. Contact tracing is also highly effective for people-gathering networks (g). Each point indicates the average value for 30 simulations. The translucent bands indicate the 95% confidence interval estimated by a bootstrapping with 104 resamples.
Contact tracing isolates fewer nodes in total, while preventing more cases than case isolation, resulting in a high cost efficiency in terms of the number of prevented cases per isolation (Fig. 3d–f). This might appear to be counterintuitive, because contact tracing isolates extra nodes (that is, contacts) in addition to case isolation. However, because this additional isolation by contact tracing preferentially targets those who are at high risk, they, in turn, prevent many subsequent transmission events, reducing the total number of isolations.
Outbreak investigation can be considered as contact tracing for ‘gatherings’ (for example, churches, grocery markets or any spontaneous gatherings; Fig. 1e)37. Note that privacy-preserving contact-tracing protocols such as DP-3T38 can be used to detect spreading events that took place in gatherings and notify risk information to those who attended the gatherings. Moreover, the people-gathering structure is found in high-temporal-resolution proximity data37 and is stable, because human mobility often follows regular routines37,39,40.
Contact tracing is effective at detecting gatherings with super-spreading events for the same reason as for super-spreaders; gatherings with k participants are detected with a probability roughly proportional to k2 (see ‘People-gathering networks’ in Methods). To test its effectiveness, we generated synthetic people-gathering networks composed of 200,000 person-nodes and 50,000 gathering-nodes with a power-law distribution of exponent −3 using the configuration model41. We then ran SEIR simulations on the network (see ‘Simulating epidemic spreading’ in Methods). Contact tracing is executed from t ≥ 0.1 in the same way as in the people contact network.
As in the case of people contact networks, contact tracing substantially reduces the peak of infections (Fig. 3g). The effectiveness of this stands out even if we isolate only 10 gatherings from a population of 200,000 people and 50,000 gatherings (Fig. 3h,i). Contact tracing isolates a comparable number of nodes as case isolation while preventing more infections, yielding a higher cost efficiency (Fig. 3j–l).
Contact tracing on a temporal contact network of students
A virus can easily spread in a densely connected population where people routinely have face-to-face contact with each other, such as students participating in the same class42,43 and workers in dorms44. Without physical distancing, epidemic control is extremely difficult. If large gatherings (for example, classes) are prohibited, there may not be strong heterogeneity in terms of the offspring distribution (no super-spreading events). In such a case, would contact tracing be useful at all?
We tested the effectiveness of contact tracing for a temporal contact network of 567 university students, which was constructed using physical contact data collected in the Copenhagen Network Study45. The physical contacts were estimated by smartphones at a resolution of 5 min. This network only captured infections among a specific population and neglected others, so it had a fairly homogeneous degree distribution, with maximum degree of 42 at 5-min resolution.
Epidemic spreading was simulated using the SEIR model (see Methods for the data pre-processing and parameters for the SEIR model). Even in this fairly homogeneous network, sampling biases are present. For example, the parents of infected nodes have a larger degree than the infected nodes in the aggregated network (Fig. 2e).
We carried out contact tracing on the third day onwards, in the same manner as for the synthetic networks, except in the way we compiled the contact list. We detected newly infected individuals with probability ps at the time when the individuals are infected. Then, with probability pt, a close contact for each detected individual was traced and added to the contact list. We considered a node a close contact if, and only if, it had had contact with the detected individual for at least 1 h in the previous seven days. Contact tracing was carried out at every 24 h interval.
Our simulations show that case isolation alone reduces the peak of infections by ~15% (Fig. 4a). Contact tracing lowers the peak by ~50%, even though the network does not exhibit strong heterogeneity (Fig. 4a). Moreover, tracing and isolating a few traced contacts has comparable effectiveness to isolating all close contacts (Fig. 4b). The peak can be further reduced by contact tracing when we can detect more infected nodes, that is, by increasing the testing capacity (Fig. 4c). Contact tracing has a marked diminishing return; as tracing probability pt increases, contact tracing isolates more nodes but prevents nearly the same number of cases (Fig. 4d–f). Still, contact tracing pays off, as it prevents at least roughly five cases per isolation. In summary, our results suggest that even when the network is homogeneous and densely connected, a small amount of contact tracing may be able to curb spreading.
An infected node is discovered and isolated with probability ps. Contact tracing isolates the most frequent n close contacts in the contact list. We isolate n = 3, 10 or all close contacts, as indicated by ‘n = 3’, ‘n = 10’ or ‘all’, respectively. a, Contact tracing reduces the peak of infections more than case isolation. b, Even if we trace and isolate a few nodes, it is as effective as isolating all contacts. c, The effectiveness is more pronounced when we can detect more infected nodes. d–f, Contact tracing isolates more nodes (d) and prevents more cases (e,f) as we trace more contacts. Contact tracing is not efficient when tracing probability is large. Although contact tracing is highly effective and efficient, massive contact tracing may have a diminishing return. Each point indicates the average value for 1,000 simulations. The translucent bands indicate the 95% confidence interval estimated by a bootstrapping with 104 resamples.
Branching process analysis of contact tracing
Let us investigate how much contact tracing would be necessary to prevent an outbreak. We calculate the epidemic probability—the probability of sustained transmission of disease—for networks with an arbitrary degree distribution under contact tracing based on a branching process formalism (see ‘Epidemic probability’ in Methods for the derivation of the probability). We consider a contact network of people, where a disease is transmitted from an infected person i (parent) to a susceptible person j (offspring) with transmission probability T. The parent is identified and isolated with probability P = pspt (that is, the tracing probability), protecting its offspring j with probability 1 − f, where failure probability f allows us to account for imperfect isolation due to individual behaviour or temporal delays in the tracing process.
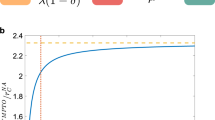
Our analytical solution (‘Epidemic probability’ in Methods), as well as a numerical simulation (Fig. 5), demonstrates that increasing the tracing probability P can control an epidemic and stop any possibility of sustained transmission while showing a diminishing return of contact tracing. Notably, we find a smooth epidemic threshold in P, which is distinct from the usual sharp epidemic threshold observed over T. This phenomenology can be understood by considering who is targeted by contact tracing. Effective execution of contact tracing detects transmission events from an individual with a probability proportional to k2, where k is the degree of the individual. Consequently, as we increase the frequency of contact tracing, we not only reduce the number of transmissions but do so by only allowing transmissions to occur around relatively small degrees. Therein lies the power of contact tracing on heterogeneous networks—it reduces the size of the epidemic and localizes it around nodes of lower degrees, reducing both the total number of infections and the frequency of super-spreading events.
We use randomized BA networks, where each of 250,000 nodes has a degree of at least 2, and attempt to control the spread of a disease with transmissibility T using tracing probability P, which successfully isolates a given sibling of a new case with probability 1 − f. Symbols show the average of 100 Monte Carlo simulations, and solid lines show the results of our analytical formalism. a, Using perfect contact tracing f = 0, the probability of sustained transmissions goes down monotonically with more contact tracing, but without undergoing the usual sharp epidemic transition. b, With f = 0, the regime of smeared epidemic transition increases with the frequency of contact tracing. At a high frequency of contact tracing, we find the probability of sustained transmission remains low, even for high values of transmissibility well beyond the epidemic threshold. c, We fix transmissibility at T = 0.3 and look at the robustness of different contact tracing probability P to imperfect tracing by varying the probability f that isolation fails.
Discussion
We show that contact tracing leverages two sampling biases arising from the heterogeneity in the number of contacts an individual has. Our theoretical and simulation analyses indicate that contact tracing can be a highly effective and efficient strategy, even when it is not performed on a massive scale, as long as it is strategically performed to leverage the sampling biases. Furthermore, contact tracing can be more cost-efficient than case isolation in terms of the number of prevented cases per isolation, particularly when detecting infection is difficult. The effectiveness and efficiency hinge on the fact that backward tracing can detect super-spreading events exceptionally well. Therefore, we argue that (1) even when massive contact tracing is not feasible, it may still be worth implementing contact tracing, (2) not all contact-tracing protocols are equal and it is crucial to implement the protocols that leverage the presented biases and (3) the ‘cheaper’ contact tracing offered by digital contact tracing may hold even greater potential than previously suggested11.
In the context of digital contact tracing, our results show the need for (1) backward contact tracing that aims to identify the parent of a detected case and (2) deep contact tracing to notify other recent contacts of the traced nodes. Current implementations of digital contact tracing, including the Apple and Google partnership46 and the DP-3T proposal38, notify the contacts of an infected individual about the risk of infection. However, they neglect that one of these previous contacts is likely the source of infection (that is, parent), who might be infecting others. We show that multiple notifications are particularly indicative of the parent and can be potentially leveraged for better intervention strategies. Therefore, we urge the consideration of a multi-step notification feature that can fully leverage the sampling biases arising from the heterogeneity in the contact network structure.
An implementation of our model does not necessarily require any compromise in terms of privacy or decentralization of the contact-tracing protocol itself47. One could also imagine a hybrid approach where deep contact tracing is undertaken using a centralized database when a given device has been notified more than a certain number of times. The benefits of such network-based contact tracing could be considerable, especially if accompanied by serious educational efforts for users to explain the rationale behind the intervention and the importance of their own role in our social network.
Although backward tracing is, in general, highly effective in heterogeneous networks, a number of factors can hinder its effectiveness. First, delays in testing, isolation and tracing steps would reduce the effectiveness of contact tracing. Backward contact tracing would be more vulnerable to such delays because it relies on the premise that we need to reach the infectors before they produce many offspring. Second, we assume that every individual has an equal probability of infection and isolation; however, this may vary depending on demographics. The heterogeneity in infection and isolation probabilities may hinder the effectiveness of opt-in contact-tracing strategies. Third, we assumed that all people are traceable, which may not be true in practice. For example, to successfully perform digital contact tracing, the tracing app may have to achieve almost universal adoption because the probability of successful contact tracing decreases by the square of the app adoption rate. On the other hand, traditional contact tracing can also fail because of those who refuse contact tracing48,49 or travelled from a different country that does not share contact data, as well as because of the imperfect recall of recent contacts, for example.
Even with the aforementioned limitations, our results suggest that contact tracing has a larger potential than commonly considered. Because its effectiveness hinges on the ability to reach the ‘source’ of infection, our results underline the importance of strategic and rapid contact-tracing protocols.
Methods
Data
We used the dataset collected in the Copenhagen Network Study45 to construct a temporal network of physical contacts between students in a university. The dataset contains information on the physical contacts between more than 700 students in a university estimated by Bluetooth signal strength. We removed all individuals from the data that had a valid Bluetooth scan in less than 60% of the observation period. We then considered that two individuals i and j had contact if i or j received Bluetooth scans from the other with a signal strength more than −75 dB. We note that this signal strength is received at a distance of ~1 m from a device50. These steps resulted in a cohort of N = 567 individuals with contact data for 28 days with resolution of 5 min.
Simulating epidemic spreading
We simulated the SEIR model for the static contact networks and people-gathering networks using the EoN package51, with transmission rate β = 0.25, recovery rate γ = 0.25, incubation rate σ = 0.25 and initial seed fraction ρ = 10−3. For the student contact network, we simulated the SEIR model with the parameters used in studies on COVID-19 disease52 (expected infectious and incubation periods were set to 5 days and 1 day, respectively. The transmission rate of COVID-19 varies highly across case studies and estimation methods11,31. One expects that, in any closed population with dense contacts, between 20 and 60% of the population are infected31. We thus use a transmission rate of 0.5 day−1 to produce outbreaks that reach 50% of the population, which is close to the worst-case scenario that might be expected on a university campus. We randomly chose 1% of the total population as initially infected nodes at time t0, where t0 was chosen randomly in the first 28 days. The epidemic spreading process may take longer than the days recorded in the contact data (that is, 28 days). Therefore, following a previous study53, we assumed that the same contact sequence for the 28 days repeats.
People-gathering networks
In the people-gathering network, a person-node is connected to a gathering-node if he/she joined the gathering. The degree of a person implies how mobile the person is across diverse sets of gatherings, and the degree of a gathering indicates the number of participants for the gathering. Denoted by G0(x) and F0(x), the generating functions for the degree distributions of persons and gatherings, respectively, are defined as
The transmission event happens from a person to others via a gathering. When we trace a gathering from a person, a gathering with k participants is k times more likely to be sampled than the gathering with only one person. Therefore, the excess size of the gathering is generated by
The probability distribution of the number of one’s neighbours through gatherings is given by G0(F1(x)). Because larger gatherings would produce more infections and thus are more likely to be traced, the number of participants of the gathering, except for the original spreader and the isolated individual, is given by the probability generating function
In other words, contact tracing samples a gathering with k participants with probability roughly proportional to k2. Therefore, as is the case for people contact networks, contact tracing is effective at identifying super-spreading events and preventing numerous further disease transmission events.
Epidemic probability
We calculated the probability that the contact tracing stops the spreading of disease. To keep the analysis simple, we assumed that every newly infected node has a probability P to lead to its parent node and we can prevent the infections to all of the parent’s grandchildren by notifying the infected node.
The probability of epidemics is determined by the offspring distributions, that is, the number of nodes to which an infected node spreads the disease. We note that the offspring distribution depends on how we sample nodes due to the sampling biases (see ‘Bias due to the friendship paradox’). Specifically, if we sample infected nodes at random or by following a random transmission, the offspring distributions are given by generating functions
respectively, where T is the probability of transmitting disease through an edge, and rk and qk are the probabilities of having k offspring, respectively.
With contact tracing, the offspring of a parent can continue the spreading process if and only if successful contact tracing does not take place for all the offspring, which occurs with probability (1 − P)k. Therefore, the nodes sampled by following a random transmission have the offspring distribution given by
where \({\overline{R}}_{1}\) denotes R1 under contact tracing, and \({\overline{R}}_{0}\) is the analogous function for R0. We have distinguished standard transmissions (counted with the variable x) from transmissions that occurred but are isolated quickly enough by contact tracing to stop the transmission tree (counted with the variable y). This gives us a way to calculate the coefficients rk of \({\overline{R}}_{0}(x,1)\), which specify the distribution of successful branching events in the transmission tree (that is, those that can continue spreading).
Because we use a multivariate PGF where the variable x counts traditional transmission events and y counts transmission with attempted isolation, the probability f of isolation failure can be implemented by replacing y with \(y^{\prime} =fx+(1-f)y\). This models a Bernoulli trial on each isolation, where failure with probability f leads to a transmission (counted by x) and where success leads to isolation (counted by y).
The probability u that transmission to a node without contact tracing around the parent does not lead to sustained transmission is given by the self-consistency condition
where the right-hand side gives the probability that the offspring also do not lead to sustained transmission (1 if successful contact tracing occurs and u otherwise). The probability of an epidemic is then the probability that at least one transmission around the patient leads to sustained transmission, or
The failure probability f should correspond to a given continuous-time epidemic model. See Supplementary Information for the calculation of failure probability f.
Data availability
The physical contact data that support the findings of this study are available from the Copenhagen Network Study with the identifier https://doi.org/10.1038/s41597-019-0325-x45. Source data are provided with this paper.
Code availability
Code is available at https://github.com/yy/backward-contact-tracing.
References
Gilbert, M., Dewatripont, M., Muraille, E., Platteau, J.-P. & Goldman, M. Preparing for a responsible lockdown exit strategy. Nat. Med. 26, 643–644 (2020).
Mattioli, A. V., Ballerini Puviani, M., Nasi, M. & Farinetti, A. COVID-19 pandemic: the effects of quarantine on cardiovascular risk. Eur. J. Clin. Nutr. 74, 852–855 (2020).
Eames, K. T. D. & Keeling, M. J. Contact tracing and disease control. Proc. R. Soc. Lond. B 270, 2565–2571 (2003).
Klinkenberg, D., Fraser, C. & Heesterbeek, H. The effectiveness of contact tracing in emerging epidemics. PLoS ONE 1, e12 (2006).
Andre, M. et al. Transmission network analysis to complement routine tuberculosis contact investigations. Am. J. Public Health 97, 470–477 (2007).
Glasser, J. W., Hupert, N., McCauley, M. M. & Hatchett, R. Modeling and public health emergency responses: lessons from SARS. Epidemics 3, 32–37 (2011).
Peak, C. M., Childs, L. M., Grad, Y. H. & Buckee, C. O. Comparing nonpharmaceutical interventions for containing emerging epidemics. Proc. Natl Acad. Sci. USA 114, 4023–4028 (2017).
Aleta, A. et al. Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19. Nat. Hum. Behav. 4, 964–971 (2020).
Ferretti, L. et al. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 368, eabb6936 (2020).
Armbruster, B. & Brandeau, M. L. Contact tracing to control infectious disease: when enough is enough. Health Care Manag. Sci. 10, 341–355 (2007).
Hellewell, J. et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 8, e488–e496 (2020).
Lloyd-Smith, J. O., Schreiber, S. J., Kopp, P. E. & Getz, W. M. Superspreading and the effect of individual variation on disease emergence. Nature 438, 355–359 (2005).
Shin, Y., Berkowitz, B. & Kim, M. J. How a South Korean church helped fuel the spread of the coronavirus. The Washington Post (25 March 2020).
Park, S. et al. Coronavirus disease outbreak in call center, South Korea. Emerg. Infect. Dis. 26, 1666–1670 (2020).
Feld, S. L. Why your friends have more friends than you do. Am. J. Sociol. 96, 1464–1477 (1991).
Christakis, N. A. & Fowler, J. H. Social network sensors for early detection of contagious outbreaks. PLoS ONE 5, e12948 (2010).
Cohen, R., Havlin, S. & Ben-Avraham, D. Efficient immunization strategies for computer networks and populations. Phys. Rev. Lett. 91, 247901 (2003).
Barthélemy, M., Barrat, A., Pastor-Satorras, R. & Vespignani, A. Dynamical patterns of epidemic outbreaks in complex heterogeneous networks. J. Theor. Biol. 235, 275–288 (2005).
Hethcote, H. W. & Yorke, J. A. Gonorrhea Transmission Dynamics and Control (Springer, 1984).
Müller, J. & Koopmann, B. The effect of delay on contact tracing. Math. Biosci. 282, 204–214 (2016).
Müller, J., Kretzschmar, M. & Dietz, K. Contact tracing in stochastic and deterministic epidemic models. Math. Biosci. 164, 39–64 (2000).
Bradshaw, W. J., Alley, E. C., Huggins, J. H., Lloyd, A. L. & Esvelt, K. M. Bidirectional contact tracing dramatically improves COVID-19 control. Nat. Commun. 12, 232 (2021).
Barlow, M. T. A branching process with contact tracing. Preprint at https://arxiv.org/pdf/2007.16182.pdf (2020).
Baumgarten, L. & Bornholdt, S. Epidemics with asymptomatic transmission: sub-critical phase from recursive contact tracing. Preprint at https://arxiv.org/pdf/2008.09896.pdf (2020).
Mülle, J. & Hósel, V. Contact tracing and super-spreaders in the branching-process model. Preprint at https://arxiv.org/pdf/2010.04942.pdf (2020).
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002).
Dorogovtsev, S. N. & Mendes, J. F. F. Evolution of Networks: From Biological Nets to the Internet and WWW (Oxford Univ. Press, 2003).
Pastor-Satorras, R. & Vespignani, A. Evolution and Structure of the Internet: A Statistical Physics Approach (Cambridge Univ. Press, 2004).
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200 (2001).
Barthélemy, M., Barrat, A., Pastor-Satorras, R. & Vespignani, A. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks. Phys. Rev. Lett. 92, 178701 (2004).
Hébert-Dufresne, L., Althouse, B. M., Scarpino, S. V. & Allard, A. Beyond R0: heterogeneity in secondary infections and probabilistic epidemic forecasting. J. R. Soc. Interface https://doi.org/10.1098/rsif.2020.0393 (2020).
Newman, M. E. Threshold effects for two pathogens spreading on a network. Phys. Rev. Lett. 95, 108701 (2005).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Meyers, L. A., Newman, M. E. J. & Pourbohloul, B. Predicting epidemics on directed contact networks. J. Theor. Biol. 240, 400–418 (2006).
Stumpf, M. P. H. & Porter, M. A. Critical truths about power laws. Science 335, 665–666 (2012).
Broido, A. D. & Clauset, A. Scale-free networks are rare. Nat. Commun. 10, 1017 (2019).
Sekara, V., Stopczynski, A. & Lehmann, S. Fundamental structures of dynamic social networks. Proc. Natl Acad. Sci. USA 113, 9977–9982 (2016).
Troncoso, C. et al. Decentralized privacy-preserving proximity tracing. Preprint at https://arxiv.org/pdf/2005.12273.pdf (2020).
Song, C., Qu, Z., Blumm, N. & Barabási, A.-L. Limits of predictability in human mobility. Science 327, 1018–1021 (2010).
Bagrow, J. P. & Lin, Y.-R. Mesoscopic structure and social aspects of human mobility. PLoS ONE 7, e37676 (2012).
Fosdick, B., Larremore, D., Nishimura, J. & Ugander, J. Configuring random graph models with fixed degree sequences. SIAM Rev. 60, 315–355 (2018).
Gemmetto, V., Barrat, A. & Cattuto, C. Mitigation of infectious disease at school: targeted class closure vs school closure. BMC Infect. Dis. 14, 695 (2014).
Darbon, A. et al. Disease persistence on temporal contact networks accounting for heterogeneous infectious periods. R. Soc. Open Sci. 6, 181404 (2019).
Sadarangani, S. P., Lim, P. L. & Vasoo, S. Infectious diseases and migrant worker health in Singapore: a receiving country’s perspective. J. Travel Med. https://doi.org/10.1093/jtm/tax014 (2017).
Sapiezynski, P., Stopczynski, A., Dreyer, D. & Lehmann, S. Interaction data from the Copenhagen Networks Study. Nat. Sci. Data 6, 315 (2019).
Apple & Google Exposure notification. Apple https://covid19.apple.com/contacttracing (2020).
Cho, H., Ippolito, D. & Yu, Y. W. Contact tracing mobile apps for COVID-19: privacy considerations and related trade-offs. Preprint at https://arxiv.org/pdf/2003.11511.pdf (2020).
Holder, S. Contact tracing is having a trust crisis. Bloomberg (12 August 2020).
Borowiec, S. How South Korea’s nightclub outbreak is shining an unwelcome spotlight on the LGBTQ community. Time (14 May 2020).
Sekara, V. & Lehmann, S. The strength of friendship ties in proximity sensor data. PLoS ONE 9, e100915 (2014).
Kiss, I. Z., Miller, J. & Simon, P. L. Mathematics of Epidemics on Networks Vol. 598 (Springer, 2017).
Zhang, J. et al. Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science 368, 1481–1486 (2020).
Valdano, E., Ferreri, L., Poletto, C. & Colizza, V. Analytical computation of the epidemic threshold on temporal networks. Phys. Rev. X 5, 021005 (2015).
Acknowledgements
We thank M. Girvan, J. Lovato and other organizers of the Net-COVID programme, which initiated the project. We also thank A. Allard, C. Moore, E. Moro, A. S. Pentland and S. V. Scarpino for helpful discussions. L.H.-D. acknowledges support from the National Institutes of Health 1P20 GM125498-01 Centers of Biomedical Research Excellence Award. S.K. and Y.-Y.A. acknowledge support from the Air Force Office of Scientific Research under award no. FA9550-19-1-0391.
Author information
Authors and Affiliations
Contributions
Y.-Y.A. conceived the research. E.M., S.K., L.H.-D. and Y.-Y.A. performed the numerical simulations. L.H.-D. and Y.-Y.A. conducted the mathematical analysis. All authors participated in the analysis and interpretation of the results as well as the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary note.
Source data
Rights and permissions
About this article
Cite this article
Kojaku, S., Hébert-Dufresne, L., Mones, E. et al. The effectiveness of backward contact tracing in networks. Nat. Phys. 17, 652–658 (2021). https://doi.org/10.1038/s41567-021-01187-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-021-01187-2
This article is cited by
-
Looking under the lamp-post: quantifying the performance of contact tracing in the United States during the SARS-CoV-2 pandemic
BMC Public Health (2024)
-
New framework to assess tracing and testing based on South Korea’s response to COVID-19
BMC Infectious Diseases (2024)
-
All paths lead to hubs in the spectroscopic networks of water isotopologues H216O and H218O
Communications Chemistry (2024)
-
Quantifying the heterogeneous impact of lockdown policies on different socioeconomic classes during the first COVID-19 wave in Colombia
Scientific Reports (2023)
-
Temporal and Probabilistic Comparisons of Epidemic Interventions
Bulletin of Mathematical Biology (2023)