Abstract
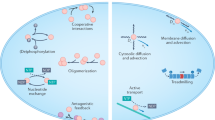
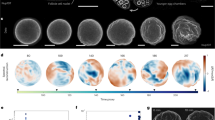
Many cellular processes, such as cell division1,2,3, cell motility4, wound healing5 and tissue folding6,7, rely on the precise positioning of proteins on the membrane. Such protein patterns emerge from a combination of protein interactions, transport, conformational state changes and chemical reactions at the molecular level8. Recent experimental and theoretical work clearly demonstrates the role of geometry, including membrane curvature9,10,11 and local cytosolic-to-membrane ratios12,13, and advective cortical flow in modulating membrane protein patterns. However, it remains unclear how these proteins achieve robust spatiotemporal organization on the membrane during the dynamic cell shape changes involved in physiological processes. Here we use oocytes of the starfish Patiria miniata as a model system to elucidate a shape-adaptation mechanism that robustly controls spatiotemporal protein dynamics on the membrane in spite of cell shape deformations. By combining experiments with biophysical theory, we show how cell shape information contained in a cytosolic gradient can be decoded by a bistable regulator of the enzyme Rho, which is associated with contractility. This bistable front in turn controls a mechanochemical response by locally triggering excitable dynamics of Rho. We posit that such a shape-adaptation mechanism based on a hierarchy of protein patterns may constitute a general physical principle for cell shape sensing and control.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code that supports the plots within this paper are described in the Methods and Supplementary Information and are available from the corresponding author upon reasonable request.
References
Théry, M. & Bornens, M. Cell shape and cell division. Curr. Opin. Cell Biol. 18, 648–657 (2006).
Minc, N., Burgess, D. & Chang, F. Influence of cell geometry on division-plane positioning. Cell 144, 414–426 (2011).
Gray, A. N. et al. Coordination of peptidoglycan synthesis and outer membrane constriction during Escherichia coli cell division. Elife 4, e07118 (2015).
Mogilner, A. & Keren, K. The shape of motile cells. Curr. Biol. 19, R762–R771 (2009).
Razzell, W., Wood, W. & Martin, P. Recapitulation of morphogenetic cell shape changes enables wound re-epithelialisation. Development 141, 1814–1820 (2014).
Heisenberg, C.-P. & Bellaïche, Y. Forces in tissue morphogenesis and patterning. Cell 153, 948–962 (2013).
Martin, A. C. & Goldstein, B. Apical constriction: Themes and variations on a cellular mechanism driving morphogenesis. Development 141, 1987–1998 (2014).
Halatek, J., Brauns, F. & Frey, E. Self-organization principles of intracellular pattern formation. Phil. Trans. R. Soc. B 373, 20170107 (2018).
Antonny, B. Mechanisms of membrane curvature sensing. Annu. Rev. Biochem. 80, 101–123 (2011).
Wu, Z., Su, M., Tong, C., Wu, M. & Liu, J. Membrane shape-mediated wave propagation of cortical protein dynamics. Nat. Commun. 9, 136 (2018).
Liu, A. P. et al. Membrane-induced bundling of actin filaments. Nat. Phys. 4, 789–793 (2008).
Thalmeier, D., Halatek, J. & Frey, E. Geometry-induced protein pattern formation. Proc. Natl Acad. Sci. USA 113, 548–553 (2016).
Rangamani, P. et al. Decoding information in cell shape. Cell 154, 1356–1369 (2013).
Harvey, E. N. & Fankhauser, G. The tension at the surface of the eggs of the salamander, Triturus (Diemyctylus) viridescens. J. Cell. Comp. Physiol. 3, 463–475 (1933).
Kojima, M. K. Cyclic changes of the cortex and the cytoplasm of the fertilized and the activated sea urchin egg. Embryologia 7, 81–94 (1962).
Hara, K., Tydeman, P. & Kirschner, M. A cytoplasmic clock with the same period as the division cycle in Xenopus eggs. Proc. Natl Acad. Sci. USA 77, 462–466 (1980).
Sawai, T. Wavelike propagation of stretching and shrinkage in the surface of the newt’s egg before the first cleavage. J. Exp. Zool. 222, 59–68 (1982).
Houliston, E., Carré, D., Johnston, J. A. & Sardet, C. Axis establishment and microtubule-mediated waves prior to first cleavage in Beroe ovata. Development 117, 75–87 (1993).
Quaas, J. & Wylie, C. Surface contraction waves (SCWs) in the Xenopus egg are required for the localization of the germ plasm and are dependent upon maternal stores of the kinesin-like protein Xklp1. Dev. Biol. 243, 272–280 (2002).
Klughammer, N. et al. Cytoplasmic flows in starfish oocytes are fully determined by cortical contractions. PLoS Comput. Biol. 14, e1006588 (2018).
Bischof, J. et al. A cdk1 gradient guides surface contraction waves in oocytes. Nat. Commun. 8, 849 (2017).
Bischof, J. The Molecular Mechanism of Surface Contraction Waves in the Starfish Oocyte. PhD thesis, Univ. Heidelberg (2016).
Wolpert, L. Positional information and pattern formation. Curr. Top. Dev. Biol. 117, 597–608 (2016).
Su, K.-C., Takaki, T. & Petronczki, M. Targeting of the RhoGEF Ect2 to the equatorial membrane controls cleavage furrow formation during cytokinesis. Dev. Cell 21, 1104–1115 (2011).
Bement, W. M. et al. Activator–inhibitor coupling between Rho signalling and actin assembly makes the cell cortex an excitable medium. Nat. Cell Biol. 17, 1471–1483 (2015).
Hodge, R. G. & Ridley, A. J. Regulating Rho GTPases and their regulators. Nat. Rev. Mol. Cell Biol. 17, 496–510 (2016).
Müller, P. M. et al. Systems analysis of RhoGEF and RhoGAP regulatory proteins reveals spatially organized RAC1 signalling from integrin adhesions. Nat. Cell Biol. 22, 498–511 (2020).
Mikhailov, A. S. Foundations of Synergetics I: Distributed Active Systems 2nd edn (Springer Science & Business Media, 2012).
Gelens, L., Anderson, G. A. & Ferrell, J. E. Spatial trigger waves: positive feedback gets you a long way. Mol. Biol. Cell 25, 3486–3493 (2014).
Wagner, E. & Glotzer, M. Local RhoA activation induces cytokinetic furrows independent of spindle position and cell cycle stage. J. Cell Biol. 213, 641–649 (2016).
Rulands, S., Klünder, B. & Frey, E. Stability of localized wave fronts in bistable systems. Phys. Rev. Lett. 110, 038102 (2013).
Green, J. B. A. & Sharpe, J. Positional information and reaction–diffusion: two big ideas in developmental biology combine. Development 142, 1203–1211 (2015).
Izhikevich, E. M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (MIT Press, 2010).
Tan, T. H. et al. Topological turbulence in the membrane of a living cell. Nat. Phys. 16, 657–662 (2020).
Howard, J., Grill, S. W. & Bois, J. S. Turing’s next steps: The mechanochemical basis of morphogenesis. Nat. Rev. Mol. Cell Biol. 12, 392–398 (2011).
Gross, P., Kumar, K. V. & Grill, S. W. How active mechanics and regulatory biochemistry combine to form patterns in development. Annu. Rev. Biophys. 46, 337–356 (2017).
Chang, J. B. & Ferrell, J. E.Jr. Mitotic trigger waves and the spatial coordination of the Xenopus cell cycle. Nature 500, 603–607 (2013).
Deneke, V. E. et al. Self-organized nuclear positioning synchronizes the cell cycle in Drosophila embryos. Cell 177, 925–941.e17 (2019).
Vergassola, M., Deneke, V. E. & Di Talia, S. Mitotic waves in the early embryogenesis of Drosophila: bistability traded for speed. Proc. Natl Acad. Sci. USA 115, E2165–E2174 (2018).
Deneke, V. E., Melbinger, A., Vergassola, M. & Di Talia, S. Waves of Cdk1 activity in S phase synchronize the cell cycle in Drosophila embryos. Dev. Cell 38, 399–412 (2016).
Curtiss, J. & Mlodzik, M. Morphogenetic furrow initiation and progression during eye development in Drosophila: the roles of decapentaplegic, hedgehog and eyes absent. Development 127, 1325–1336 (2000).
Benink, H. A. & Bement, W. M. Concentric zones of active RhoA and Cdc42 around single cell wounds. J. Cell Biol. 168, 429–439 (2005).
Su, K.-C., Bement, W. M., Petronczki, M. & von Dassow, G. An astral simulacrum of the central spindle accounts for normal, spindle-less, and anucleate cytokinesis in echinoderm embryos. Mol. Biol. Cell 25, 4049–4062 (2014).
Gökirmak, T. et al. Localization and substrate selectivity of sea urchin multidrug (MDR) efflux transporters. J. Biol. Chem. 287, 43876–43883 (2012).
Acknowledgements
We thank P. Lenart, J. Bischof, K. Keren, A. Martin, A. Goryachev and E. Zanin for discussions. We also thank W. Salmon and staff at the W.M. Keck Microscopy Facility at the Whitehead Institute for microscopy support. E.F. acknowledges the hospitality of the Kavli Institute of Nanoscience at the Delft University of Technology where part of this work was done. This research was supported by a National Science Foundation CAREER award (to N.F.), a German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) fellowship within the Graduate School of Quantitative Biosciences Munich (to M.C.W.), the Joachim Herz Foundation (to M.C.W.), the DFG via B2 projects within the Collaborative Research Center SFB 1032 (to E.F.), and the DFG via the Research Training Group GRK 2062 (to F.B.). This research was supported in part by the National Science Foundation under grant no. NSF PHY-1748958.
Author information
Authors and Affiliations
Contributions
T.H.T. and N.F. initiated the project and designed the experiments. T.H.T. and J.L. performed the experiments and analysed the experimental data. M.C.W., F.B. and E.F. designed the model. M.C.W. performed the simulations and analysed the simulation data. S.Z.S. contributed reagents. All authors participated in interpreting the experimental and theoretical results and in writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Leah Edelstein-Keshet, Nicolas Minc and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–21, Tables 1 and 2, theoretical derivations and references.
Supplementary Video 1
Surface contraction wave of starfish oocyte during meiosis I. Rho-GTP is labelled fluorescently using rGBD-GFP reporter. Video taken with confocal microscopy at cross-section (left) and bottom plane (right) of oocytes. Time in min:s.
Supplementary Video 2
Rho-GTP wave (labelled with rGBD-GFP) of starfish oocyte during meiosis I when imaged in an elliptical PDMS chamber with AP at one corner. Video taken with confocal microscopy at cross-section of oocyte. Time in min:s.
Supplementary Video 3
Rho-GTP wave (labelled with rGBD-GFP) of starfish oocyte during meiosis I when imaged in an elliptical PDMS chamber with AP at side. Video taken with confocal microscopy at cross-section of oocyte. Time in min:s.
Supplementary Video 4
Rho-GTP wave (labelled with rGBD-GFP) of starfish oocyte during meiosis I when imaged in a triangular PDMS chamber with AP in the middle. Video taken with confocal microscopy at cross-section of oocyte. Time in min:s.
Supplementary Video 5
Rho-GTP wave (labelled with rGBD-GFP) of starfish oocyte during meiosis I when imaged in a star shape PDMS chamber with AP at one corner. Video taken with confocal microscopy at cross-section of oocyte. Time in min:s.
Supplementary Video 6
Spatiotemporal dynamics of Cdk1-cyclinB cytosolic gradient during meiosis I in starfish oocyte. The Cdk1 complex is imaged with cyclinB-GFP fluorescent reporter. Video taken with confocal microscopy at cross-section of oocyte. Time in min:s.
Supplementary Video 7
Spatiotemporal dynamics of Cdk1-cyclinB cytosolic gradient during meiosis I in starfish oocyte in ellipse with AP at one side. Video taken with confocal microscopy at cross-section of oocyte. Time in min:s.
Supplementary Video 8
Spatiotemporal dynamics of Cdk1-cyclinB cytosolic gradient during meiosis I in starfish oocyte in triangle with AP at one side. Video taken with confocal microscopy at cross-section of oocyte. Time in min:s.
Supplementary Video 9
Spatiotemporal dynamics of Cdk1-cyclinB cytosolic gradient during meiosis I in starfish oocyte in triangle with AP at one corner. Video taken with confocal microscopy at cross-section of oocyte. Time in min:s.
Supplementary Video 10
Dynamics of Rho-GTP spiral front at the oocyte membrane imaged using fluorescently labelled reporter rGBD-GFP. Time in min:s.
Supplementary Video 11
Ect2-mCherry front dynamics at the membrane. Owing to significant auto-fluorescent from cortex granules, we performed background subtraction by taking the cumulative sum of the fluorescent intensity difference (same procedure as for Ect2 space–time kymograph). The left video shows the raw data. The right video shows the background subtracted video. Note that the intensity around the periphery of oocyte in background subtracted video is due to the oocyte motion during surface contraction wave. Time in min:s.
Supplementary Video 12
Two-colour imaging of Ect2 (Ect2-mCherry fluorescent reporter) front and Rho-GTP (rGBD-GFP reporter) spiral front. Time in min:s.
Supplementary Video 13
Two-colour imaging of Cdk1-cyclinB (cyclinB-GFP fluorescent reporter) gradient and Ect2 (Ect2-mCherry fluorescent reporter) front. Time in min:s.
Supplementary Video 14
Simulation of the Rho model (see equations (1) and (2) in the Supplementary Information) on the surface of a spherical 3D volume using parameters for the wild type as specified in Supplementary Table 1.
Supplementary Video 15
Simulations of the Rho and Ect2 module in ellipsoidal 3D geometries. Left panel shows the Cdk1 concentration (log10(k[Cdk1])) in the cytoplasm and Rho-GTP (urt) on the membrane, and middle and right panels show the active Ect2 concentration (ue + uE) and the Rho-GTP concentration (urt) on the surface of the 3D geometry.
Supplementary Video 16
Simulations of the Rho and Ect2 module in triangular 3D geometries. Left panel shows the Cdk1 concentration (log10(k[Cdk1])) in the cytoplasm and Rho-GTP (urt) on the membrane, and middle and right panels show the active Ect2 concentration (ue + uE) and the Rho-GTP concentration (urt) on the surface of the 3D geometry
Supplementary Video 17
Simulations of the Rho and Ect2 module in star-shaped 3D geometries. Left panel shows the Cdk1 concentration (log10(k[Cdk1])) in the cytoplasm and Rho-GTP (urt) on the membrane, and middle and right panels show the active Ect2 concentration (ue + uE) and the Rho-GTP concentration (urt) on the surface of the 3D geometry.
Supplementary Video 18
Simulation of the Rho model (see equations (1) and (2) in the Supplementary Information) on the surface of a spherical 3D volume using parameters for Ect2 overexpression as specified in Supplementary Table 1.
Supplementary Video 19
Photoactivation experiment. Global light illumination at 488 nm begins at 0 s. Increase in yellow fluorescence indicates the recruitment of PR_GEF_YFP (photo-recruitable GEF labelled with yellow fluorescent protein) to the membrane. Beyond a certain threshold level, the oocyte contractility abruptly increases.
Supplementary Video 20
Maximal intensity projection of microtubule front near oocyte membrane during surface contraction wave imaged using ensconsin-GFP. Time in min:s.
Rights and permissions
About this article
Cite this article
Wigbers, M.C., Tan, T.H., Brauns, F. et al. A hierarchy of protein patterns robustly decodes cell shape information. Nat. Phys. 17, 578–584 (2021). https://doi.org/10.1038/s41567-021-01164-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-021-01164-9
This article is cited by
-
Hierarchical graph learning for protein–protein interaction
Nature Communications (2023)
-
Control of protein-based pattern formation via guiding cues
Nature Reviews Physics (2022)
-
Forced and spontaneous symmetry breaking in cell polarization
Nature Computational Science (2022)