Abstract
Entanglement is an essential property of multipartite quantum systems, characterized by the inseparability of quantum states of objects regardless of their spatial separation. Generation of entanglement between increasingly macroscopic and disparate systems is an ongoing effort in quantum science, as it enables hybrid quantum networks, quantum-enhanced sensing and probing of the fundamental limits of quantum theory. The disparity of hybrid systems and the vulnerability of quantum correlations have thus far hampered the generation of macroscopic hybrid entanglement. Here, we generate an entangled state between the motion of a macroscopic mechanical oscillator and a collective atomic spin oscillator, as witnessed by an Einstein–Podolsky–Rosen variance below the separability limit, 0.83 ± 0.02 < 1. The mechanical oscillator is a millimetre-size dielectric membrane and the spin oscillator is an ensemble of 109 atoms in a magnetic field. Light propagating through the two spatially separated systems generates entanglement because the collective spin plays the role of an effective negative-mass reference frame and provides—under ideal circumstances—a back-action-free subspace; in the experiment, quantum back-action is suppressed by 4.6 dB.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
References
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Chen, Y. Macroscopic quantum mechanics: theory and experimental concepts of optomechanics. J. Phys. B 46, 104001 (2013).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Kurizki, G. et al. Quantum technologies with hybrid systems. Proc. Natl. Acad. Sci. USA 112, 3866–3873 (2015).
Cirac, J. I. & Zoller, P. Quantum computations with cold trapped ions. Phys. Rev. Lett. 74, 4091–4094 (1995).
Gross, C. & Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 357, 995–1001 (2017).
Brown, K. R., Kim, J. & Monroe, C. Co-designing a scalable quantum computer with trapped atomic ions. npj Quant. Inf. 2, 16034 (2016).
Hammerer, K., Aspelmeyer, M., Polzik, E. S. & Zoller, P. Establishing Einstein-Poldosky-Rosen channels between nanomechanics and atomic ensembles. Phys. Rev. Lett. 102, 020501 (2009).
Manukhova, A. D., Rakhubovsky, A. A. & Filip, R. Pulsed atom-mechanical quantum non-demolition gate. npj Quant. Inf. 6, 4 (2020).
Julsgaard, B., Kozhekin, A. & Polzik, E. S. Experimental long-lived entanglement of two macroscopic objects. Nature 413, 400–403 (2001).
Polzik, E. S. & Hammerer, K. Trajectories without quantum uncertainties. Ann. Phys. 527, A15–A20 (2015).
Møller, C. B. et al. Quantum back-action-evading measurement of motion in a negative mass reference frame. Nature 547, 191–195 (2017).
Tsang, M. & Caves, C. M. Coherent quantum-noise cancellation for optomechanical sensors. Phys. Rev. Lett. 105, 123601 (2010).
Hammerer, K., Sørensen, A. S. & Polzik, E. S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 82, 1041–1093 (2010).
Muschik, C. A., Polzik, E. S. & Cirac, J. I. Dissipatively driven entanglement of two macroscopic atomic ensembles. Phys. Rev. A 83, 052312 (2011).
Krauter, H. et al. Entanglement generated by dissipation and steady state entanglement of two macroscopic objects. Phys. Rev. Lett. 107, 080503 (2011).
Stannigel, K., Rabl, P. & Zoller, P. Driven-dissipative preparation of entangled states in cascaded quantum-optical networks. New J. Phys. 14, 063014 (2012).
Vasilyev, D. V., Muschik, C. A. & Hammerer, K. Dissipative versus conditional generation of Gaussian entanglement and spin squeezing. Phys. Rev. A 87, 053820 (2013).
Huang, X. et al. Unconditional steady-state entanglement in macroscopic hybrid systems by coherent noise cancellation. Phys. Rev. Lett. 121, 103602 (2018).
Tsang, M. & Caves, C. M. Evading quantum mechanics: engineering a classical subsystem within a quantum environment. Phys. Rev. X 2, 031016 (2012).
Kohler, J., Gerber, J. A., Dowd, E. & Stamper-Kurn, D. M. Negative-mass instability of the spin and motion of an atomic gas driven by optical cavity backaction. Phys. Rev. Lett. 120, 013601 (2018).
Karg, T. M. et al. Light-mediated strong coupling between a mechanical oscillator and atomic spins 1 meter apart. Science 369, 174–179 (2020).
Jöckel, A. et al. Sympathetic cooling of a membrane oscillator in a hybrid mechanical–atomic system. Nat. Nanotechnol. 10, 55–59 (2015).
Christoph, P. et al. Combined feedback and sympathetic cooling of a mechanical oscillator coupled to ultracold atoms. New J. Phys. 20, 093020 (2018).
Tan, H., Buchmann, L. F., Seok, H. & Li, G. Achieving steady-state entanglement of remote micromechanical oscillators by cascaded cavity coupling. Phys. Rev. A 87, 022318 (2013).
Woolley, M. J. & Clerk, A. A. Two-mode back-action-evading measurements in cavity optomechanics. Phys. Rev. A 87, 063846 (2013).
Ockeloen-Korppi, C. F. et al. Stabilized entanglement of massive mechanical oscillators. Nature 556, 478–482 (2018).
Riedinger, R. et al. Remote quantum entanglement between two micromechanical oscillators. Nature 556, 473–477 (2018).
Lee, K. C. et al. Entangling macroscopic diamonds at room temperature. Science 334, 1253–1256 (2011).
Tsaturyan, Y., Barg, A., Polzik, E. S. & Schliesser, A. Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution. Nat. Nanotechnol. 12, 776–783 (2017).
Borregaard, J. et al. Scalable photonic network architecture based on motional averaging in room temperature gas. Nat. Commun. 7, 11356 (2016).
Holstein, T. & Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 58, 1098–1113 (1940).
Duan, L.-M., Giedke, G., Cirac, J. I. & Zoller, P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2722–2725 (2000).
Müller-Ebhardt, H. et al. Quantum-state preparation and macroscopic entanglement in gravitational-wave detectors. Phys. Rev. A 80, 043802 (2009).
Rossi, M., Mason, D., Chen, J. & Schliesser, A. Observing and verifying the quantum trajectory of a mechanical resonator. Phys. Rev. Lett. 123, 163601 (2019).
Wieczorek, W. et al. Optimal state estimation for cavity optomechanical systems. Phys. Rev. Lett. 114, 223601 (2015).
Wasilewski, W. et al. Quantum noise limited and entanglement-assisted magnetometry. Phys. Rev. Lett. 104, 133601 (2010).
Balabas, M. V. et al. High quality anti-relaxation coating material for alkali atom vapor cells. Opt. Express 18, 5825–5830 (2010).
Geremia, J. M., Stockton, J. K. & Mabuchi, H. Tensor polarizability and dispersive quantum measurement of multilevel atoms. Phys. Rev. A 73, 042112 (2006).
Lammers, J. State Preparation and Verification in Continuously Measured Quantum Systems. PhD thesis, Leibniz University Hannover (2018).
Higginbotham, A. P. et al. Harnessing electro-optic correlations in an efficient mechanical converter. Nat. Phys. 14, 1038–1042 (2018).
Mirhosseini, M., Sipahigil, A., Kalaee, M. & Painter, O. Quantum transduction of optical photons from a superconducting qubit. Preprint at https://arxiv.org/abs/2004.04838 (2020).
Khalili, F. Y. & Polzik, E. S. Overcoming the standard quantum limit in gravitational wave detectors using spin systems with a negative effective mass. Phys. Rev. Lett. 121, 031101 (2018).
Zeuthen, E., Polzik, E. S. & Khalili, F. Y. Gravitational wave detection beyond the standard quantum limit using a negative-mass spin system and virtual rigidity. Phys. Rev. D 100, 062004 (2019).
Foreman-Mackey, D., Hogg, D. W., Lang, D. & Goodman, J. emcee: The MCMC hammer. Publ. Astron. Soc. Pac. 125, 306–312 (2013).
Acknowledgements
We acknowledge conversations with K. Hammerer and J. H. Müller. X. Huang contributed theoretical simulations in the early stages of the project. We acknowledge M. Balabas for fabricating the coated caesium cells. This project has been supported by the European Research Council Advanced grant QUANTUM-N, the Villum Foundation and John Templeton Foundation. E.Z. acknowledges funding from the Carlsberg Foundation. M.P. was partially supported by the Foundation for Polish Science (FNP). R.A.T. was partially funded by the programme Science without Borders of the Brazilian Federal Government.
Author information
Authors and Affiliations
Contributions
E.S.P. conceived and led the project. R.A.T., C.B.M., C.Ø. and M.P. built the experiment with the help of C.B. and J.A. The membrane resonator was conceived by A.S. and Y.T. designed and fabricated the device. R.A.T., M.P., C.Ø., C.B.M. and C.B. collected the data. E.Z. and M.P. developed the theory with input from J.A., E.S.P. and R.A.T. The paper was written by E.S.P., E.Z., R.A.T., M.P., C.Ø., C.B.M. and C.B., with contributions from other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Details of the experimental set-up and of supporting theory including Supplementary Figs. 1–8 and Table 1.
Source data
Source Data Fig. 1
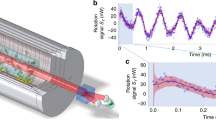
A trajectory of the oscillator.
Source Data Fig. 3
Noise spectra; Wiener filter.
Source Data Fig. 4
Noise spectra and theory fits; conditional variance.
Rights and permissions
About this article
Cite this article
Thomas, R.A., Parniak, M., Østfeldt, C. et al. Entanglement between distant macroscopic mechanical and spin systems. Nat. Phys. 17, 228–233 (2021). https://doi.org/10.1038/s41567-020-1031-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-1031-5
This article is cited by
-
Ultrahigh-quality-factor micro- and nanomechanical resonators using dissipation dilution
Nature Nanotechnology (2024)
-
Acoustic frequency atomic spin oscillator in the quantum regime
Nature Communications (2023)
-
Mechanically-tunable bandgap closing in 2D graphene phononic crystals
npj 2D Materials and Applications (2023)
-
Optomechanics for quantum technologies
Nature Physics (2022)
-
The QBIT Theory: Consciousness from Entangled Qubits
Integrative Psychological and Behavioral Science (2022)