Abstract
The influence of geometry on the local and global packing of particles is important to many fundamental and applied research themes, such as the structure and stability of liquids, crystals and glasses. Here we show by experiments and simulations that a binary mixture of hard-sphere-like nanoparticles crystallizing into a MgZn2 Laves phase in bulk spontaneously forms icosahedral clusters in slowly drying droplets. Using advanced electron tomography, we are able to obtain the real-space coordinates of all the spheres in the icosahedral clusters of up to about 10,000 particles. The local structure of 70–80% of the particles became similar to that of the MgCu2 Laves phase. These observations are important for photonic applications. In addition, we observed in simulations that the icosahedral clusters nucleated away from the spherical boundary, which is distinctly different from that of the single species clusters. Our findings open the way for particle-level studies of nucleation and growth of icosahedral clusters, and of binary crystallization.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
All data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
Code availability
Computer simulations were performed using HOOMD-blue, available at http://glotzerlab.engin.umich.edu/hoomd-blue/.
References
1. Turnbull, D. in Solid State Physics (eds Seitz, F. & Turnbull, D.) Vol. 3, 225–306 (Elsevier, 1956).
Frank, F. C. Supercooling of liquids. Proc. R. Soc. Lond. A 215, 43–46 (1952).
Taffs, J. & Royall, C. P. The role of fivefold symmetry in suppressing crystallization. Nat. Commun. 7, 13225 (2016).
Steinhardt, P. J., Nelson, D. R. & Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 28, 784–805 (1983).
Nelson, D. R. & Spaepen, F. in Solid State Physics (eds Ehrenreich, H. & Turnbull, D.) Vol. 42, 1–90 (Elsevier, 1989).
Spaepen, F. Condensed-matter science: five-fold symmetry in liquids. Nature 408, 781–782 (2000).
Van Blaaderen, A. & Wiltzius, P. Real-space structure of colloidal hard-sphere glasses. Science 270, 1177–1179 (1995).
Gasser, U., Weeks, E. R., Schofield, A., Pusey, P. N. & Weitz, D. A. Real-space imaging of nucleation and growth in colloidal crystallization. Science 292, 258–262 (2001).
Kegel, W. K. & van Blaaderen, A. Direct observation of dynamical heterogeneities in colloidal hard-sphere suspensions. Science 287, 290–293 (2000).
Cheng, Z. Colloidal Crystallization Ch. 12, 203–248 (John Wiley & Sons, 2016).
Fernandez-Nieves, A. & Puertas, A. M. Fluids, Colloids and Soft Materials: An Introduction to Soft Matter Physics Vol. 7 (John Wiley & Sons, 2016).
Wintzheimer, S. et al. Supraparticles: functionality from uniform structural motifs. ACS Nano 12, 5093–5120 (2018).
Wang, T., LaMontagne, D., Lynch, J., Zhuang, J. & Cao, Y. C. Colloidal superparticles from nanoparticle assembly. Chem. Soc. Rev. 42, 2804–2823 (2013).
De Nijs, B. et al. Entropy-driven formation of large icosahedral colloidal clusters by spherical confinement. Nat. Mater. 14, 56–60 (2015).
Lacava, J., Born, P. & Kraus, T. Nanoparticle clusters with Lennard–Jones geometries. Nano Lett. 12, 3279–3282 (2012).
Yang, Y. et al. Scalable assembly of crystalline binary nanocrystal superparticles and their enhanced magnetic and electrochemical properties. J. Am. Chem. Soc. 140, 15038–15047 (2018).
Wang, J. et al. Magic number colloidal clusters as minimum free energy structures. Nat. Commun. 9, 5259 (2018).
Wang, D. et al. Interplay between spherical confinement and particle shape on the self-assembly of rounded cubes. Nat. Commun. 9, 2228 (2018).
Wang, J. et al. Free energy landscape of colloidal clusters in spherical confinement. ACS Nano 13, 9005–9015 (2019).
Laves, F. & Witte, H. Der einfluß von valenzelektronen auf die kristallstruktur ternärer magnesiumlegierungen. Metallwirtschaft 15, 840–842 (1936).
Berry, R. L. & Raynor, G. V. The crystal chemistry of the Laves phases. Acta Cryst. 6, 178–186 (1953).
Hynninen, A.-P., Filion, L. & Dijkstra, M. Stability of LS and LS2 crystal structures in binary mixtures of hard and charged spheres. J. Chem. Phys. 131, 064902 (2009).
Hynninen, A.-P., Thijssen, J. H. J., Vermolen, E. C. M., Dijkstra, M. & van Blaaderen, A. Self-assembly route for photonic crystals with a bandgap in the visible region. Nat. Mater. 6, 202–205 (2007).
Dong, A., Chen, J., Vora, P. M., Kikkawa, J. M. & Murray, C. B. Binary nanocrystal superlattice membranes self-assembled at the liquid–air interface. Nature 466, 474–477 (2010).
Saghi, Z. & Midgley, P. A. Electron tomography in the (S)TEM: from nanoscale morphological analysis to 3D atomic imaging. Annu. Rev. Mater. Res. 42, 59–79 (2012).
Bals, S., Goris, B., Liz-Marzán, L. M. & Van Tendeloo, G. Three-dimensional characterization of noble-metal nanoparticles and their assemblies by electron tomography. Angew. Chem. Int. Ed. 53, 10600–10610 (2014).
Zanaga, D. et al. Quantitative 3D analysis of huge nanoparticle assemblies. Nanoscale 8, 292–299 (2016).
Wang, P.-p, Qiao, Q., Zhu, Y. & Ouyang, M. Colloidal binary supracrystals with tunable structural lattices. J. Am. Chem. Soc. 140, 9095–9098 (2018).
Chen, O. et al. Magneto-fluorescent core-shell supernanoparticles. Nat. Commun. 5, 5093 (2014).
Kister, T., Mravlak, M., Schilling, T. & Kraus, T. Pressure-controlled formation of crystalline, Janus, and core–shell supraparticles. Nanoscale 8, 13377–13384 (2016).
Yang, Z. et al. Supracrystalline colloidal eggs: epitaxial growth and free standing three-dimensional supracrystals in nanoscaled colloidosomes. J. Am. Chem. Soc. 138, 3493–3500 (2016).
Anderson, J. A., Lorenz, C. D. & Travesset, A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 227, 5342 – 5359 (2008).
Glaser, J. et al. Strong scaling of general-purpose molecular dynamics simulations on GPUs. Comput. Phys. Commun. 192, 97 – 107 (2015).
Bergman, G., Waugh, J. L. & Pauling, L. The crystal structure of the metallic phase Mg32(Al, Zn)49. Acta Cryst. 10, 254–259 (1957).
Lechner, W. & Dellago, C. Accurate determination of crystal structures based on averaged local bond order parameters. J. Chem. Phys. 129, 114707 (2008).
Yang, Z. et al. Precipitation of binary quasicrystals along dislocations. Nat. Commun. 9, 809 (2018).
Ducrot, É., He, M., Yi, G.-R. & Pine, D. J. Colloidal alloys with preassembled clusters and spheres. Nat. Mater. 16, 652–657 (2017).
Wang, Y., Jenkins, I. C., McGinley, J. T., Sinno, T. & Crocker, J. C. Colloidal crystals with diamond symmetry at optical lengthscales. Nat. Commun. 8, 14173 (2017).
Pietryga, J. M. et al. Utilizing the lability of lead selenide to produce heterostructured nanocrystals with bright, stable infrared emission. J. Am. Chem. Soc. 130, 4879–4885 (2008).
Steckel, J. S., Yen, B. K. H., Oertel, D. C. & Bawendi, M. G. On the mechanism of lead chalcogenide nanocrystal formation. J. Am. Chem. Soc. 128, 13032–13033 (2006).
Evers, W. H. et al. Entropy-driven formation of binary semiconductor-nanocrystal superlattices. Nano Lett. 10, 4235–4241 (2010).
Mason, T. G. & Bibette, J. Shear rupturing of droplets in complex fluids. Langmuir 13, 4600–4613 (1997).
Guizar-Sicairos, M., Thurman, S. T. & Fienup, J. R. Efficient subpixel image registration algorithms. Opt. Lett. 33, 156–158 (2008).
Gilbert, P. Iterative methods for the three-dimensional reconstruction of an object from projections. J. Theor. Biol. 36, 105–117 (1972).
Martyna, G. J., Tobias, D. J. & Klein, M. L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 101, 4177–4189 (1994).
Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984).
Hoover, W. G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697 (1985).
Acknowledgements
D.W., E.B.v.d.W. and A.v.B. acknowledge partial financial support from the European Research Council under the European Union’s Seventh Framework Programme (FP-2007-2013)/ERC Advanced Grant Agreement 291667 HierarSACol. T.D. and M.D. acknowledge financial support from the Industrial Partnership Programme, ‘Computational Sciences for Energy Research’ (grant number 13CSER025), of the Netherlands Organization for Scientific Research (NWO), which was co-financed by Shell Global Solutions International BV G.M.C. was also financially supported by NWO. S.B. acknowledges financial support from ERC Consolidator Grant Number 815128 REALNANO. T.A. acknowledges a post-doctoral grant from the Research Foundation Flanders (FWO, Belgium). C.B.M. and Y.W. acknowledge support for materials synthesis from the Office of Naval Research Multidisciplinary University Research Initiative Award ONR N00014-18-1-2497. G. A. Blab is gratefully acknowledged for 3D printing numerous truncated tetrahedra, which increased our understanding of the connection between the binary icosahedral cluster and Laves phase structures. N. Tasios is sincerely thanked for providing the code for the diffraction pattern calculation. M. Hermes is sincerely thanked for providing interactive views of the structures in this work. We thank G. van Tendeloo, M. Engel, J. Wang, S. Dussi, L. Filion, E. Boattini, S. Paliwal, N. Tasios, B. van der Meer, I. Lobato, J. Wu and L. Laurens for fruitful discussions. We acknowledge the EM Square centre at Utrecht University for the access to the microscopes.
Author information
Authors and Affiliations
Contributions
A.v.B. initiated the investigation of icosahedral order in binary crystals under spherical confinement and supervised D.W. and E.B.v.d.W. M.D. initiated the simulation study on the binary icosahedral clusters in spherical confinement and supervised T.D. and G.M.C. T.D. performed computer simulations of the spontaneous nucleation of binary icosahedral clusters. D.W. synthesized the SPs and obtained, together with T.A., the electron tomography. D.Z. performed SSR tomographic reconstruction and T.A. performed manual segmentations, under the supervision of S.B. Y.W. synthesized NCs under the supervision of C.B.M. E.B.v.d.W., T.D. and G.M.C. developed the BOP analysis of the Laves phases, the binary icosahedral clusters and the cluster criterion to track the nucleation of the binary icosahedral clusters. D.W., T.D., E.B.v.d.W., M.D. and A.v.B. analysed the results. A.v.B., M.D., D.W., T.D. and E.B.v.d.W. co-wrote the manuscript. All authors discussed the text and interpretation of the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary methods, Tables 1 and 2, Figs. 1–13 and refs. 1–12.
Supplementary Data 1
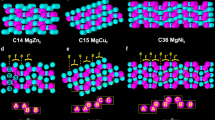
Crystal structure of the MgZn2 Laves phase.
Supplementary Data 2
Crystal structure of the MgCu2 Laves phase.
Supplementary Data 3
Crystal structure of the MgNi2 Laves phase.
Supplementary Data 4
An experimental binary icosahedral cluster supraparticle composed of 2,609 nanocrystals, with a size ratio of 0.78.
Supplementary Data 5
A simulated binary icosahedral cluster supraparticle composed of 5,001 HS-like particles with a size ratio of 0.78, after compression.
Supplementary Data 6
Cluster made up of the first eight shells from the centre of symmetry, of a simulated binary icosahedral cluster supraparticle composed of 5,001 HS-like particles with a size ratio of 0.78, after compression.
Supplementary Data 7
Cluster made up of the first eight shells from the centre of symmetry, of an experimental binary icosahedral cluster supraparticle composed of 2,609 nanocrystals.
Supplementary Data 8
Pentagonal tubes composed of alternating pentagons of L and S particles, in a simulated binary icosahedral cluster supraparticle composed of 5,001 HS-like particles with a size ratio of 0.78, after compression.
Supplementary Data 9
Pentagonal tubes composed of alternating pentagons of L and S particles, in an experimental binary icosahedral cluster supraparticle composed of 2,609 nanocrystals.
Supplementary Video 1
HAADF-STEM tilt series of an experimental binary icosahedral cluster supraparticle with a diameter of 110 nm, consisting of 2,609 nanocrystals.
Supplementary Video 2
Three-dimensional representation and orthoslices views of the reconstructed binary icosahedral cluster supraparticle with a diameter of 110 nm by SSR algorithm. Large PbSe nanocrystals and small CdSe nanocrystals are coloured in cyan and red, respectively.
Supplementary Video 3
HAADF-STEM tilt series of an experimental binary icosahedral cluster supraparticle with a diameter of 187 nm, consisting of 9,898 nanocrystals.
Supplementary Video 4
Three-dimensional representation and orthoslices views of the reconstructed binary icosahedral cluster supraparticle with a diameter of 187 nm by SSR algorithm. Large PbSe nanocrystals and small CdSe nanocrystals are coloured in cyan and red, respectively.
Supplementary Video 5
A video showing the nucleation of a binary icosahedral cluster in computer simulation (Ntot = 5,001). Different crystalline domains are shown in different colours. Particles not belonging to the binary icosahedral cluster are reduced in size for visual clarity.
Source data
Source Data Fig. 2
Coordinates of six experimental supraparticles and two simulated supraparticles composed of Ntot = 3,501 and Ntot = 5,001 HS-like particles.
Source Data Supplementary Table 2
Coordinates of a simulated supraparticles composed of Ntot = 10,002 HS-like particles.
Source Data Fig. 5
Plots of the fraction of crystalline particles as a function of the radial distance from the centre of the supraparticle (Ntot = 5,001) at different molecular dynamics times.
Rights and permissions
About this article
Cite this article
Wang, D., Dasgupta, T., van der Wee, E.B. et al. Binary icosahedral clusters of hard spheres in spherical confinement. Nat. Phys. 17, 128–134 (2021). https://doi.org/10.1038/s41567-020-1003-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-1003-9
This article is cited by
-
Crystallization of binary nanocrystal superlattices and the relevance of short-range attraction
Nature Synthesis (2023)
-
Entropically engineered formation of fivefold and icosahedral twinned clusters of colloidal shapes
Nature Communications (2022)
-
Structural diversity in three-dimensional self-assembly of nanoplatelets by spherical confinement
Nature Communications (2022)
-
Design of platinum single-atom doped metal nanoclusters as efficient oxygen reduction electrocatalysts by coupling electronic descriptor
Nano Research (2022)
-
Quantitative 3D real-space analysis of Laves phase supraparticles
Nature Communications (2021)