Abstract
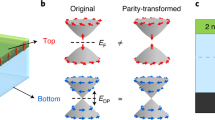
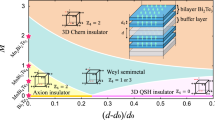
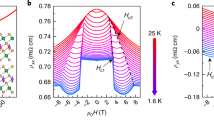
The quantum anomalous Hall effect1,2 is a fundamental transport response of a topological insulator in zero magnetic field. Its physical origin is a result of an intrinsically inverted electronic band structure and ferromagnetism3, and its most important manifestation is the dissipationless flow of chiral charge currents at the edges of the system4, a property that has the potential to transform future quantum electronics5,6. Here, we report a Berry-curvature-driven4,7 anomalous Hall regime at temperatures of several Kelvin in the magnetic topological bulk crystals in which Mn ions self-organize into a period-ordered MnBi2Te4/Bi2Te3 superlattice. Robust ferromagnetism of the MnBi2Te4 monolayers opens a surface gap8,9,10, and when the Fermi level is tuned to be within this gap, the anomalous Hall conductance reaches an e2/h quantization plateau, which is a clear indication of chiral transport through the edge states. The quantization in this regime is not obstructed by the bulk conduction channels and therefore should be present in a broad family of topological magnets.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are available for this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Liu, C. -X., Zhang, S. -C. & Qi, X. -L. The quantum anomalous Hall effect: theory and experiment. Annu. Rev. Condens. Matter Phys. 7, 301–321 (2016).
Zhang, J., Zhao, B., Zhou, T. & Yang, Z. Quantum anomalous Hall effect in real materials. Chin. Phys. B 25, 117308 (2016).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effects. Rev. Mod. Phys. 82, 1539–1592 (2010).
Qi, X. -L., Hughes, T. & Zhang, S. -C. Chiral topological superconductor from the quantum Hall state. Phys. Rev. B. 82, 184516 (2010).
Smejkal, L., Mokrousov, Y., Yan, B. & MacDonald, A. Topological antiferromagnetic spintronics. Nat. Phys. 14, 242–251 (2018).
Xiao, D., Chang, M. -C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Rienks, E. et al. Large magnetic gap at the Dirac point in Bi2Te3/MnBi2Te4 heterostructure. Nature 576, 423–431 (2019).
Otrokov, M. et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 576, 416–422 (2019).
Hu, C. et al. A van der Waals antiferromagnetic topological insulator with weak interlayer magnetic coupling. Nat. Commun. 11, 97 (2020).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Haldane, D. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the ‘parity anomaly’. Phys. Rev. Lett. 61, 2015–2018 (1988).
Qi, X. -L. & Zhang, S. -C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Chang, C. -Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Chen, Y. et al. Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010).
Feng, X. et al. Thickness dependence of the quantum anomalous Hall effect in magnetic topological insulator films. Adv. Mater. 28, 6386–6390 (2016).
Wang, W. et al. Direct evidence of ferromagnetism in a quantum anomalous Hall system. Nat. Phys. 14, 791–795 (2018).
Lee, I. et al. Imaging Dirac-mass disorder from magnetic dopant atoms in the ferromagnetic topological insulator Crx(Bi0.1Sb0.9)2−xTe3. Proc. Natl Acad. Sci. USA 112, 1316–1321 (2015).
Zhang, J., Zhao, B., Zhou, T. & Yang, Z. Quantum anomalous Hall effect in real materials. Chin. Phys. B 25, 117308 (2016).
Kou, X. et al. Metal-to-insulator switching in quantum anomalous Hall states. Nat. Commun. 6, 8474 (2015).
Mogi, M. et al. Magnetic modulation doping in topological insulators toward higher-temperature quantum anomalous Hall effect. Appl. Phys. Lett. 107, 182401 (2015).
Burkov, A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Scanlon, D. et al. Controlling bulk conductivity in topological insulators: key role of anti-site defects. Adv. Mater. 24, 2154–2158 (2012).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009).
Lee, D. et al. Crystal structure, properties and nanostructuring of a new layered chalcogenide semiconductor, Bi2MnTe4. Cryst. Eng. Comm. 15, 5532 (2013).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Otrokov, M. et al. Highly-ordered wide bandgap materials for quantized anomalous Hall and magnetoelectric effects. 2D Mater. 4, 025082 (2017).
Deng, Y. et al. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 367, 895–900 (2020).
Zhao, L. et al. Stable topological insulators achieved using high energy electron beams. Nat. Commun. 7, 10957 (2016).
Hu, S. M. Atomic Diffusion in Semiconductors (ed. Shaw, D.) 217 (Springer, 1973).
Bahramy, M. S. et al. Emergent quantum confinement at topological insulator surfaces. Nat. Commun. 3, 1159 (2012).
Checkelsky, J. et al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator. Nat. Phys. 10, 731–736 (2014).
Xu, Y., Miotkowski, I. & Chen, Y. Quantum transport of two-species Dirac fermions in dual-gated three-dimensional topological insulators. Nat. Commun. 7, 11434 (2016).
Chen, T. et al. High-mobility Sm-doped Bi2Se3 ferromagnetic topological insulators and robust exchange coupling. Adv. Mater. 27, 4823–4829 (2015).
Yue, C. et al. Symmetry-enforced chiral hinge states and surface quantum anomalous Hall effect in the magnetic axion insulator Bi2−xSmxSe3. Nat. Phys. 15, 577–581 (2019).
Hor, Y. et al. Development of ferromagnetism in the doped topological insulator Bi2−xMnxTe3. Phys. Rev. B 81, 195203 (2010).
Checkelsky, J. G., Ye, J., Onose, Y., Iwasa, Y. & Tokura, Y. Dirac-fermion mediated ferromagnetism in a topological insulator. Nat. Phys. 8, 729–733 (2012).
Acknowledgements
We wish to acknowledge A. Millis for helpful insights and J. Hone for critical reading of the manuscript. This work was supported by the US National Science Foundation grants DMR-1420634 (Columbia-CCNY MRSEC) and HRD-1547830, and by the Polish National Science Center grant 2016/21/B/ST3/02565. Irradiations on SIRIUS platform were supported by EMIR&A under project 18-9136. Computational support was provided by Virginia Tech Advanced Research for Computing and the San Diego Supercomputer Center under DMR-060009N.
Author information
Authors and Affiliations
Contributions
Experiments were designed by L.K.-E. and H.D. Device fabrication and the transport and magnetic measurements were performed by H.D. Structural and elemental characterization of the crystals grown by I.V.F. was done by K.S. and J.B. A.W. and J.S. characterized samples by ferromagnetic resonance. Electron irradiations were conducted by M.K. with the assistance of Z.C. and H.D. ARPES studies were performed by T.H. and L.P. K.P. calculated the DFT band structure. A.B.G. and J.C. calculated AHE conductance from the Berry curvature. Data analysis was done by H.D. and L.K.-E. L.K.-E. wrote the manuscript with the input from H.D.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Discussion and Supplementary Figures 1–14
Source data
Source Data Fig. 1
Source data for Figure 1.
Source Data Fig. 2
Source data for Figure 2.
Source Data Fig. 3
Source data for Figure 3.
Source Data Fig. 4
Source data for Figure 4.
Rights and permissions
About this article
Cite this article
Deng, H., Chen, Z., Wołoś, A. et al. High-temperature quantum anomalous Hall regime in a MnBi2Te4/Bi2Te3 superlattice. Nat. Phys. 17, 36–42 (2021). https://doi.org/10.1038/s41567-020-0998-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0998-2
This article is cited by
-
Quantum-metric-induced nonlinear transport in a topological antiferromagnet
Nature (2023)
-
High Curie temperature ferromagnetic structures of (Sb2Te3)1−x(MnSb2Te4)x with x = 0.7–0.8
Scientific Reports (2023)
-
High Chern number van der Waals magnetic topological multilayers MnBi2Te4/hBN
npj 2D Materials and Applications (2023)
-
Axion optical induction of antiferromagnetic order
Nature Materials (2023)
-
Rashba-like physics in condensed matter
Nature Reviews Physics (2022)