Abstract
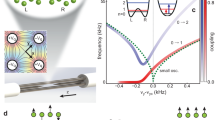
Quantum measurement remains a puzzle through its stormy history from the birth of quantum mechanics to state-of-the-art quantum technologies. Two complementary measurement schemes have been widely investigated in a variety of quantum systems: von Neumann’s projective ‘strong’ measurement and Aharonov’s weak measurement. Here, we report the observation of a weak-to-strong measurement transition in a single trapped 40Ca+ ion system. The transition is realized by tuning the interaction strength between the ion’s internal electronic state and its vibrational motion, which play the roles of the measured system and the measuring pointer, respectively. By pre- and post-selecting the internal state, a pointer state composed of two of the ion’s motional wavepackets is obtained, and its central-position shift, which corresponds to the measurement outcome, demonstrates the transition from the weak-value asymptotes to the expectation-value asymptotes. Quantitatively, the weak-to-strong measurement transition is characterized by a universal transition factor \({e}^{-{\varGamma }^{2}/2}\), where Γ is a dimensionless parameter related to the system–apparatus coupling. This transition, which continuously connects weak measurements and strong measurements, may open new experimental possibilities to test quantum foundations and prompt us to re-examine and improve the measurement schemes of related quantum technologies.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
References
Von Neumann, J. Mathematical Foundations of Quantum Mechanics: New Edition (Princeton University Press, 2018).
Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351–1354 (1988).
Berry, M. V. & Shukla, P. Typical weak and superweak values. J. Phys. A 43, 354024 (2010).
Hosoya, A. & Shikano, Y. Strange weak values. J. Phys. A 43, 385307 (2010).
Pusey, M. F. Anomalous weak values are proofs of contextuality. Phys. Rev. Lett. 113, 200401 (2014).
Piacentini, F. Experiment investigating the connection between weak values and contextuality. Phys. Rev. Lett. 116, 180401 (2016).
Avella, A. Anomalous weak values and the violation of a multiple-measurement Leggett-Garg inequality. Phys. Rev. A 96, 052123 (2017).
Aharonov, Y., Cohen, E., Carmi, A. & Elitzur, A. C. Extraordinary interactions between light and matter determined by anomalous weak values. Proc. R. Soc. A 474, 20180030 (2018).
Hosten, O. & Kwiat, P. Observation of the spin Hall effect of light via weak measurements. Science 319, 787–790 (2008).
Dixon, P. B., Starling, D. J., Jordan, A. N. & Howell, J. C. Ultrasensitive beam deflection measurement via interferometric weak value amplification. Phys. Rev. Lett. 102, 173601 (2009).
Jordan, A. N., Rincón, J. M. & Howell, J. C. Technical advantages for weak-value amplification: when less is more. Phys. Rev. X 4, 011031 (2014).
Aharonov, Y., Botero, A., Popescu, S., Reznik, B. & Tollaksen, J. Revisiting Hardy’s paradox: counterfactual statements, real measurements, entanglement and weak values. Phys. Lett. A 301, 130–138 (2002).
Lundeen, J. S. & Steinberg, A. M. Experimental joint weak measurement on a photon pair as a probe of Hardy’s paradox. Phys. Rev. Lett. 102, 020404 (2009).
Kocsis, S. et al. Observing the average trajectories of single photons in a two-slit interferometer. Science 332, 1170–1173 (2011).
Aharonov, Y. & Rohrlich, D. Quantum Paradoxes: Quantum Theory for the Perplexed (Wiley-VCH, 2005).
Chen, M.-C. et al. Experimental demonstration of quantum pigeonhole paradox. Proc. Natl Acad. Sci. USA 116, 1549–1552 (2019).
Denkmayr, T. et al. Observation of a quantum Cheshire Cat in a matter–wave interferometer experiment. Nat. Commun. 5, 4492 (2004).
Dressel, J., Broadbent, C. J., Howell, J. C. & Jordan, A. N. Experimental violation of two-party Leggett-Garg inequalities with semiweak measurements. Phys. Rev. Lett. 106, 040402 (2011).
Dziewior, J. et al. Universality of local weak interactions and its application for interferometric alignment. Proc. Natl. Acad. Sci. USA 116, 2881–2890 (2019).
Vaidman, L. et al. Weak value beyond conditional expectation value of the pointer readings. Phys. Rev. A 96, 032114 (2017).
Duck, I. M., Stevenson, P. M. & Sudarshan, E. C. G. The sense in which a ‘weak measurement’ of a spin-1/2 particle’s spin component yields a value 100. Phys. Rev. D 40, 2112–2117 (1989).
Kofman, A. G., Ashhab, S. & Nori, F. Nonperturbative theory of weak pre- and post-selected measurements. Phys. Rep. 520, 43–133 (2012).
Tamir, B., Cohen, E. & Priel, A. On the power of weak measurements in separating quantum states. Quant. Stud. Math. Found. 2, 37–49 (2015).
Piacentini, F. et al. Investigating the effects of the interaction intensity in a weak measurement. Sci. Rep. 8, 6959 (2018).
Leibfried, D., Blatt, R., Monroe, C. & Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75, 281–324 (2003).
Häffner, H., Roos, C. F. & Blatt, R. Quantum computing with trapped ions. Phys. Rep. 469, 155–203 (2008).
Schindler, P. et al. A quantum information processor with trapped ions. New J. Phys. 15, 123012 (2013).
Wu, C. W. et al. Scheme and experimental demonstration of fully atomic weak-value amplification. Phys. Rev. A 100, 062111 (2019).
Harris, J., Boyd, R. W. & Lundeen, J. S. Weak value amplification can outperform conventional measurement in the presence of detector saturation. Phys. Rev. Lett. 118, 070802 (2017).
Magaña-Loaiza, O. S. et al. Weak-value measurements can outperform conventional measurements. Phys. Scripta 92, 023001 (2017).
Di Lorenzo, A. & Egues, J. C. Weak measurement: effect of the detector dynamics. Phys. Rev. A 77, 042108 (2008).
Pan, A. K. & Matzkin, A. Weak values in nonideal spin measurements: an exact treatment beyond the asymptotic regime. Phys. Rev. A 85, 022122 (2012).
Palacios-Laloy, A. et al. Experimental violation of a Bell’s inequality in time with weak measurement. Nat. Phys. 6, 442–447 (2010).
Pang, S., Brun, T. A., Wu, S. & Chen, Z. B. Amplification limit of weak measurements: a variational approach. Phys. Rev. Lett. 90, 012108 (2014).
Silva, R., Gisin, N., Guryanova, Y. & Popescu, S. Multiple observers can share the nonlocality of half of an entangled pair by using optimal weak measurements. Phys. Rev. Lett. 114, 250401 (2015).
Susa, Y., Shikano, Y. & Hosoya, A. Optimal probe wave function of weak-value amplification. Phys. Rev. A 85, 052110 (2012).
Shomroni, I. et al. Demonstration of weak measurement based on atomic spontaneous emission. Phys. Rev. Lett. 111, 023604 (2013).
Monroe, C., Meekhof, D. M., King, B. E. & Wineland, D. J. A. ‘Schrödinger Cat’ superposition state of an atom. Science 272, 1131–1136 (1996).
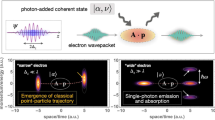
Pan, Y. et al. Weak measurement, projective measurement and quantum-to-classical transitions in electron–photon interactions. Preprint at https://arxiv.org/abs/1910.11685 (2019).
Acknowledgements
This work was supported in part by DIP (German–Israeli Project Cooperation) and by the I-CORE Israel Center of Research Excellence programme of the ISF and by the Crown Photonics Center, and was also supported by the National Basic Research Program of China under grant no. 2016YFA0301903 and the National Natural Science Foundation of China under grant nos. 61632021 and 11574398. E.C. acknowledges support from the Israeli Innovation Authority under project no. 70002 and from the Quantum Science and Technology Program of the Israeli Council of Higher Education.
Author information
Authors and Affiliations
Contributions
Y.P. and E.C. proposed the concept and the modelling. Y.P., J.Z., C.W. and P.C. contributed to the theoretical analysis, design and setting up of the experiments. J.Z. and C.W. performed the atom experiment, and analysed the data together with Y.P. and E.C. All authors contributed to the writing and revision of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. A1–A3, experimental set-up details and data analysis method.
Supplementary Data 1
Source data for Supplementary Fig. 2. Probability distribution of motional wavepacket with Γ = 2.9, θ = 0.02.
Supplementary Data 2
Source data for Supplementary Fig. 3. Fitting method for extracting the averaged position of the motional wavepacket with the parameters Γ = 0.4, θ = 0.2.
Source data
Source Data Fig. 2
Data for characterizing the overlapping extent of the cat state’s superposed wavepackets.
Source Data Fig. 3
The measurement regimes in the full parameter space (Γ, θ).
Rights and permissions
About this article
Cite this article
Pan, Y., Zhang, J., Cohen, E. et al. Weak-to-strong transition of quantum measurement in a trapped-ion system. Nat. Phys. 16, 1206–1210 (2020). https://doi.org/10.1038/s41567-020-0973-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0973-y
This article is cited by
-
Weak measurements and quantum-to-classical transitions in free electron–photon interactions
Light: Science & Applications (2023)
-
Demonstration of the quantum principle of least action with single photons
Nature Photonics (2023)
-
Quantum-coherence-free precision metrology by means of difference-signal amplification
Scientific Reports (2023)
-
Time-series quantum reservoir computing with weak and projective measurements
npj Quantum Information (2023)
-
Self-testing of a single quantum system from theory to experiment
npj Quantum Information (2023)