Abstract
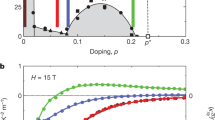
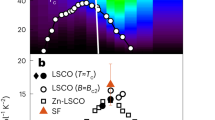
The nature of the pseudogap phase of hole-doped cuprate superconductors is still not understood fully. Several experiments have suggested that this phase ends at a critical hole doping level p*, but the nature of the ground state for lower doping is still debated. Here, we use local nuclear magnetic resonance and bulk ultrasound measurements to show that, once competing effects from superconductivity are removed by high magnetic fields, the spin-glass phase of La2−xSrxCuO4 survives up to a doping level consistent with p*. In this material, the antiferromagnetic-glass phase extends from the doped Mott insulator at p = 0.02 up to p* ≈ 0.19, which provides a connection between the pseudogap and the physics of the Mott insulator. Furthermore, the coincidence of the pseudogap boundary with a magnetic quantum phase transition in the non-superconducting ground state has implications for the interpretation of other experiments, particularly for transport and specific-heat measurements in high magnetic fields.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Data are available from the corresponding authors upon request.
References
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Proust, C. & Taillefer, L. The remarkable underlying ground states of cuprate superconductors. Annu. Rev. Condens. Matter Phys. 10, 409–429 (2019).
Julien, M.-H. Magnetic order and superconductivity in La2−xSrxCuO4: a review. Phys. B 329, 693 (2003).
Niedermayer, C. H. et al. Common phase diagram for antiferromagnetism in La2−xSrxCuO4 and Y1−xCaxBa2Cu3O6 as seen by muon spin rotation. Phys. Rev. Lett. 80, 3843–3846 (1998).
Julien, M.-H. et al. Charge segregation, cluster spin glass, and superconductivity in La1.94Sr0.06CuO4. Phys. Rev. Lett. 83, 604–607 (1999).
Panagopoulos, C. et al. Low-frequency spins and the ground state in high-Tc cuprates. Solid State Commun. 126, 47–55 (2003).
Risdiana et al. Cu spin dynamics in the overdoped regime of La2−xSrxCu1−yZnyO4 probed by muon spin rotation. Phys. Rev. B. 77, 054516 (2008).
Haug, D. et al. Neutron scattering study of the magnetic phase diagram of underdoped YBa2Cu3O6+x. New J. Phys. 12, 105006 (2010).
Wu, T. et al. Magnetic-field-enhanced spin freezing on the verge of charge ordering in YBa2Cu3O6.45. Phys. Rev. B 88, 014511 (2013).
Sasagawa, T., Mang, P. K., Vajk, O. P., Kapitulnik, A. & Greven, M. Bulk magnetic properties and phase diagram of Li-doped La2CuO4: Common magnetic response of hole-doped CuO2 planes. Phys. Rev. B 66, 184512 (2002).
Kimura, H. et al. Novel in-gap spin state in Zn-doped La1.85Sr0.15CuO4. Phys. Rev. Lett. 91, 067002 (2003).
Tallon, J. L., Loram, J. W. & Panagopoulos, C. Pseudogap and quantum-transition phenomenology in HTS cuprates. J. Low Temp. Phys. 131, 387–394 (2003).
Julien, M.-H. et al. 63Cu NMR evidence for enhanced antiferromagnetic correlations around Zn impurities in YBa2Cu3O6.7. Phys. Rev. Lett. 84, 3422–3425 (2000).
Alloul, H., Bobroff, J., Gabay, M. & Hirschfeld, P. J. Defects in correlated metals and superconductors. Rev. Mod. Phys. 81, 45–108 (2009).
Li, Y. et al. Low-energy antiferromagnetic spin fluctuations limit the coherent superconducting gap in cuprates. Phys. Rev. B 98, 224508 (2018).
Lake, B. et al. Antiferromagnetic order induced by an applied magnetic field in a high-temperature superconductor. Nature 415, 299–302 (2002).
Khaykovich, B. et al. Field-induced transition between magnetically disordered and ordered phases in underdoped La2−xSrxCuO4. Phys. Rev. B 71, 220508 (2005).
Chang, J. et al. Tuning competing orders in La2−xSrxCuO4 cuprate superconductors by the application of an external magnetic field. Phys. Rev. B 78, 104525 (2008).
Lake, B. et al. Spins in the vortices of a high-temperature superconductor. Science 291, 1759–1762 (2001).
Tranquada, J. M. et al. Evidence for an incommensurate magnetic resonance in La2−xSrxCuO4. Phys. Rev. B 69, 174507 (2004).
Mitrović, V. F. et al. Similar glassy features in the 139La NMR response of pure and disordered La1.88Sr0.12CuO4. Phys. Rev. B 78, 014504 (2008).
Arsenault, A. et al. 139La NMR investigation of the charge and spin order in a La1.885Sr0.115CuO4 single crystal. Phys. Rev. B 97, 064511 (2018).
Baek, S.-H., Erb, A. & Büchner, B. Low-energy spin dynamics and critical hole concentrations in La2−xSrxCuO4 (0.07 ≤ x ≤ 0.2) revealed by 139La and 63Cu nuclear magnetic resonance. Phys. Rev. B 96, 094519 (2017).
Curro, N. J. et al. Inhomogeneous low frequency spin dynamics in La1.65Eu0.2Sr0.15CuO4. Phys. Rev. Lett. 85, 642 (2000).
Doussineau, P., Levelut, A., Matecki, M., Renard, J. P. & Schön, W. Acoustic and magnetic studies of an insulating spin glass. EPL 3, 251 (1987).
Demler, E., Sachdev, S. & Zhang, Y. Spin-ordering quantum transitions of superconductors in a magnetic field. Phys. Rev. Lett. 87, 067202 (2001).
Kivelson, S. A., Lee, D.-H., Fradkin, E. & Oganesyan, V. Competing order in the mixed state of high-temperature superconductors. Phys. Rev. B 66, 144516 (2002).
Park, T. et al. Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn5. Nature 440, 65–68 (2006).
Kang, H. J. et al. Antiferromagnetic order as the competing ground state in electron-doped Nd1.85Ce0.15CuO4. Nature 423, 522–525 (2003).
Wakimoto, S. et al. Disappearance of antiferromagnetic spin excitations in overdoped La2−xSrxCuO4. Phys. Rev. Lett. 98, 247003 (2007).
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Croft, T. P., Lester, C., Senn, M. S., Bombardi, A. & Hayden, S. M. Charge density wave fluctuations in La2−xSrxCuO4 and their competition with superconductivity. Phys. Rev. B 89, 224513 (2014).
Wen, J. J. et al. Observation of two types of charge density wave orders in superconducting La2−xSrxCuO4. Nat. Commun. 10, 3269 (2019).
Parcollet, O. & Georges, A. Non-Fermi-liquid regime of a doped Mott insulator. Phys. Rev. B 59, 5341–5360 (1999).
Sordi, G., Haule, K. & Tremblay, A.-M. S. Finite Doping Signatures of the Mott Transition in the Two-Dimensional Hubbard Model. Phys. Rev. Lett. 104, 226402 (2010).
Boebinger, G. S. et al. Insulator-to-metal crossover in the normal state of La2−xSrxCuO4 near optimum doping. Phys. Rev. Lett. 77, 5417–5420 (1996).
Balakirev, F. F. et al. Quantum phase transition in the magnetic-field-induced normal state of optimum-doped high-Tc cuprate superconductors at low temperatures. Phys. Rev. Lett. 102, 017004 (2009).
Cooper, R. A. et al. Anomalous criticality in the electrical resistivity of La2−xSrxCuO4. Science 323, 603–607 (2009).
Collignon, C. et al. Fermi-surface transformation across the pseudogap critical point of the cuprate superconductor La1.6−xNd0.4SrxCuO4. Phys. Rev. B 95, 224517 (2017).
Bourgeois-Hope, P. et al. Link between magnetism and resistivity upturn in cuprates: a thermal conductivity study of La2−xSrxCuO4. Preprint at https://arxiv.org/abs/1910.08126 (2019).
Millis, A. J. & Norman, M. R. Antiphase stripe order as the origin of electron pockets observed in 1/8-hole-doped cuprates. Phys. Rev. B 76, 220503 (2007).
Sun, X. F., Komiya, S., Takeya, J. & Ando, Y. Magnetic-field-induced localization of quasiparticles in underdoped La2−xSrxCuO4 single crystals. Phys. Rev. Lett. 90, 117004 (2003).
Panagopoulos, C. & Dobrosavljević, V. Self-generated electronic heterogeneity and quantum glassiness in the high-temperature superconductors. Phys. Rev. B 72, 014536 (2005).
Michon, B. et al. Thermodynamic signatures of quantum criticality in cuprate superconductors. Nature 567, 218–222 (2019).
Hücker, M. et al. Enhanced charge stripe order of superconducting La2−xBaxCuO4 in a magnetic field. Phys. Rev. B 87, 014501 (2013).
Singer, P. M., Hunt, W. A. & Imai, T. 63Cu NQR evidence for spatial variation of hole concentration in La2−xSrxCuO4. Phys. Rev. Lett. 88, 047602 (2002).
Yu, Y. & Kivelson, S. A. Fragile superconductivity in the presence of weakly disordered charge density waves. Phys. Rev. B 99, 144513 (2019).
Leridon, B. et al. Protected superconductivity at the boundaries of charge-density-wave domains. Preprint at https://arxiv.org/abs/1905.05606 (2019).
Nohara, M. et al. Interplay between lattice softening and high-Tc superconductivity in La1.86Sr0.14CuO4. Phys. Rev. Lett. 70, 3447 (1993).
Wakimoto, S. et al. Incommensurate lattice distortion in the high temperature tetragonal phase of La2−x(Sr,Ba)xCuO4. J. Phys. Soc. Jpn. 75, 074714 (2006).
Takagi, H. et al. Disappearance of superconductivity in overdoped La2−xSrxCuO4 at a structural phase boundary. Phys. Rev. Lett. 68, 3777–3780 (1992).
Lüthi, B. Physical acoustics in the solid state 1st edn, (Springer-Verlag, 2005).
Varshni, P. Temperature dependence of the elastic constants. Phys. Rev. B 2, 3952–3958 (1970).
Nohara, M. et al. Unconventional lattice stiffening in superconducting La2−xSrxCuO4 single crystals. Phys. Rev. B 52, 570–580 (1995).
Acknowledgements
We thank G. S. Boebinger, A. Böhmer, N. B. Christensen, Y. Gallais, A. Georges, M. Greven, Z. Guguchia, S. M. Hayden, M. Horvatić, S. A. Kivelson, T. Klein, N. Laflorencie, M. Le Tacon, W. Metzner, C. Pépin, D. Popović, B. Ramshaw, A. T. Rømer, J. Schmalian, L. Taillefer, J. M. Tranquada and A. -M. Tremblay for discussions. Part of this work was performed at the LNCMI, a member of the European Magnetic Field Laboratory. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the US National Science Foundation Cooperative Agreement no. DMR-1644779 and the State of Florida. Work in Grenoble was supported by the Laboratoire d’Excellence LANEF (ANR-10-LABX-51-01). Work in Toulouse was supported through the EUR grant NanoX no. ANR-17-EURE-0009. Work at the LNCMI was supported by the French Agence Nationale de la Recherche (ANR) under reference ANR-19-CE30-0019 (Neptun). Work in Beijing was supported by the National Natural Science Foundation of China (grant nos. 11674377, 11634015 and 11974405), MOST grants (no. 2016YFA0300502 and no. 2017YFA0302904) and the Strategic Priority Research Program of the Chinese Academy of Sciences (grant no. XDB33010100). Work in Zürich was supported by the Swiss National Science Foundation. S.O. acknowledges support from JSPS KAKENHI grant no. JP17H01052.
Author information
Authors and Affiliations
Contributions
M.F., S.B., S.W., C.P. and D.L. performed the ultrasound experiments. I.V., R.Z., H.M., S.K., S.K.R., A.P.R. and M.-H.J. performed the NMR experiments. M.F. and I.V. analysed experimental data with suggestions from D.L. and M.-H.J. T.K., N.M., M.O., S.K., S.O., M.H. and J.C. provided single crystals. M.F. and J.D. cut precisely oriented single crystals. D.L. and M.-H.J. supervised the project and wrote the manuscript with suggestions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Yuji Furukawa, Subir Sachdev and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Stretching exponent β in NMR T1 measurements.
a, Stretching exponent β for different fields in La1.852Sr0.148CuO4. b, Stretching exponent β for Sr concentrations x = p. The stretching exponent provides a phenomenological measure of the width of the distribution of T1 values (ref.21 and references therein).
Extended Data Fig. 2 Comparison of Tf from NMR and Tmin from sound velocity.
In the upper panel we show the temperature dependence of 1/T1 calculated within the BPP model with a correlation time 𝜏c α exp(1/T). Within this model, 1/T1 features a maximum when 𝜔 𝜏c = 1. This maximum occurs at T = Tf the freezing temperature at the NMR time scale. In the lower panel we plot the temperature dependence of the sound velocity 𝚫v/v calculated within the dynamical susceptibility model that applies to canonical spin glass systems25. We use the same correlation time 𝜏c as for 1/T1 calculation and we use a Curie-like susceptibility (T) α 1/T. In contrast with 1/T1, the condition 𝜔 𝜏c = 1 results in an inflexion point in 𝚫v/v. The sound velocity minimum at Tmin is found slightly higher than Tf, as observed experimentally. The temperature dependence of the sound velocity can be understood as follows. At high temperature, when the ultrasound frequency ωUS is such that ωUS << τc−1, a softening arises from the slowing down of acoustic phonons by magnetic fluctuations, through magneto-elastic coupling. On the other hand, in the frozen state at low temperature, when ωUS >> τc−1, the acoustic phonons decouple from the slowly fluctuating moments leading to the hardening upon cooling. In between these two asymptotic behaviours, Δv/v must go through a minimum at a temperature Tmin.
Extended Data Fig. 3 Field dependence of glassy freezing.
a–d, Field dependence of 139La 1/T1 at T = 1.7 K for different doping levels. The minimum at low fields arises from the balance between an increase of 1/T1 upon increasing B (field-induced spin freezing) and a frequency effect (1/T1 decreases with increasing NMR frequency, itself proportional to B – see Methods). Dashed lines are guides to the eye. e–h, Field dependence of the sound velocity for different doping levels. In contrast to NMR, ultrasound is measured at constant frequency as a function of field. For each sample with a doping level p < p*, the field dependence is plotted at a temperature where Δv/v decreases upon cooling, that is for T ≥ Tmin (see Fig. 1). For p = 0.215, Δv/v is plotted at the lowest T achieved during the experiment. For p < p* and field B || c, Δv/v is almost field independent at low fields and above a doping-dependent onset field Bslow, it shows a strong 1/B dependence, highlighted in panels i–l. For B || (110) (panel g), Δv/v shows no softening, and only increases up to 84 T. This highlights that the field effect arises from competition with superconductivity. i–l, Inverse field dependent sound velocity (Δv/v - χ0)−1 + χ0−1, where χ0 is a doping-dependent constant (χ0 = 0.5 x 10−3 for p = 0.148, χ0 = 2.2 x 10−3 for p = 0.168, χ0 = 0.3 x 10−3 for p = 0.188 and χ0 = 0.4 x 10−3 for p = 0.215). For p < p*, (Δv/v - χ0)−1 is linear as a function of B for B > Bslow (pointed by arrows), with Bslow increasing with doping, as shown in Fig. 4. At doping level p = 0.168 and for T = 4.2 K, (Δv/v - χ0)−1 deviates from linearity for B > 70 T, which probably signals the proximity to spin freezing. For p ≈ 0.21, both the weak field induced softening (h,i) and the field dependence of 1/T1 (d) stop at about 40 T, a field value consistent with the upper critical field Bc2 (Supplementary Fig. 2). The field dependence below 40 T is explained by the suppression of superconductivity in both cases.
Extended Data Fig. 4 Contrasting NMR T1 data below and above p* = 0.19.
a–c, Temperature dependence of 139La 1/T1T in a field of 15 T for different doping levels. The peak in 1/T1T around 180 K (x = 0.155) and 140 K (x = 0.171) is due to the tetragonal-to-orthorhombic structural transition (electric-field gradient fluctuations contributing to the nuclear relaxation through quadrupolar interaction), the drop below 40 K (all samples) is due to superconductivity and the low T upturn is due to glassy slowing down. This latter is not observed for x = 0.21. Also, for this x = 0.21 sample, the T dependence in the normal state as well as the large residual 1/T1T value in the T = 0 limit are both due to the structural transition at T ≈ 6 K (that is, the relaxation peak produced by electric-field gradient fluctuations becomes very broad). Lines are guides to the eye.
Extended Data Fig. 5 1/T1 data vs. T.
Data (same as in Fig. 3 but not divided by T) are shown at selected values of the magnetic fields for each sample. Error bars are s.d. from fits of the nuclear-magnetization recoveries to a stretched-exponential form (see Methods). Lines guide the eye through the highest-field data.
Extended Data Fig. 6 Pulsed field sound velocity data at all doping levels.
a–d, Field dependence of the sound velocity, Δv/v(B), at different temperatures for p = 0.148 (panel a), p = 0.168 (panel b), p = 0.188 (panel c) and p = 0.215 (panel d). The data were obtained at the following measurement frequencies: f=225 MHz (p = 0.148), f = 172 MHz (p = 0.168), f = 187 MHz (p = 0.188) and f = 244 MHz (p = 0.215). Curves are shifted vertically for clarity. All data presented here are from the downsweep part of the magnetic field pulse. From those data, cuts at constant magnetic field are made in order to obtain the temperature dependence of the field induced sound velocity.
Extended Data Fig. 7 Determination of the field scale Bslow in NMR data.
a, Field dependence of 139La 1/T1 at T = 1.7 K for different doping levels. The minimum at low fields arises from the balance between an increase of 1/T1 upon increasing B (field-induced spin freezing) and a frequency effect (1/T1 decreases with increasing NMR frequency, itself proportional to B). Lines represent the estimated field dependence of the superconducting background (see Supplementary Fig. 3). b, Relaxation rate 1/T1, sub after subtraction of the superconducting background. c, B/T1,sub values. The multiplication by B accounts for the 1/B dependence of 1/T1 (see Methods). The Bslow value for each sample (marked by arrows) is determined from the criterion B/T1, sub = 0.166 T s−1, chosen so as to match neutron scattering results, namely Bslow = 7 T for x = 0.148 (see Methods). Dashed lines are guides to the eye.
Extended Data Fig. 8 Ultrasound attenuation across p*.
In canonical spin glass systems, the slowing down of magnetic fluctuations produces a peak in the ultrasound attenuation α25. The origin of this peak is similar to that of the NMR relaxation rate 1/T1 peak: when the condition 𝜔US 𝜏c = 1 is satisfied, a peak develops and defines the freezing temperature at the ultrasound time scale. In the left panel we show such an attenuation peak for our sample with p = 0.168, that clearly develops in high fields. This is further evidence that a slowing down, and a freezing, of magnetic fluctuations occur in high field in this sample. In the right panel we show the ultrasound attenuation measured in our sample with p = 0.215 > p*. At this doping level no attenuation peak is observed up to the highest field achieved during the experiment. This confirms the absence of freezing in this sample.
Extended Data Fig. 9 Studied samples and their structural transition.
High temperature tetragonal (HTT) to low temperature orthorhombic (LTO) transition temperature Tst of NMR (green) and US (blue) samples plotted as a function of doping. The doping of the NMR and US samples is evaluated by comparing Tst with original published data shown as black symbols50,51, as indicated in the legend. For p ≤ 0.188, we used the simple linear relation \(T_{st}\left( p \right) = 522 - 2221 \times p\) (dashed line) to extract the doping of our samples. The continuous line is a guide to the eye that indicates a critical doping of p ≈ 0.21 for the structural transition.
Extended Data Fig. 10 Structural transition HTT-LTO observed in sound velocity.
Sound velocity of the mode (c11-c12)/2 shows a plateau at Tst, signaling the high temperature tetragonal (HTT) to low temperature orthorhombic (LTO) phase transition, in agreement with previous report54. Arrows indicate Tst for each doping. For the sample p = 0.215 no sign of the structural phase transition is seen down to T = 7 K and we therefore used Tc to determine the hole doping of this sample.
Supplementary information
Supplementary Information
Supplementary Figs. 1–3 and Supplementary Table 1.
Rights and permissions
About this article
Cite this article
Frachet, M., Vinograd, I., Zhou, R. et al. Hidden magnetism at the pseudogap critical point of a cuprate superconductor. Nat. Phys. 16, 1064–1068 (2020). https://doi.org/10.1038/s41567-020-0950-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0950-5
This article is cited by
-
Theoretical understanding of correlation between magnetic phase transition and the superconducting dome in high-Tc cuprates
Science China Physics, Mechanics & Astronomy (2024)
-
Low-Field Hall effect, Pseudogap and Magnetic Textures in the Bi\(_{2}\)Sr\(_{2}\)CaCu\(_{2}\)O\(_{8+x}\) Superconductor
Journal of Superconductivity and Novel Magnetism (2024)
-
Spin fluctuations associated with the collapse of the pseudogap in a cuprate superconductor
Nature Physics (2023)
-
Fate of charge order in overdoped La-based cuprates
npj Quantum Materials (2023)
-
Reconciling scaling of the optical conductivity of cuprate superconductors with Planckian resistivity and specific heat
Nature Communications (2023)