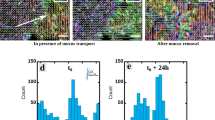
Abstract
Mucus clearance constitutes the primary defence of the respiratory system against viruses, bacteria and environmental insults. This transport across the entire airway emerges from the integrated activity of thousands of multiciliated cells, each containing hundreds of cilia, which together must coordinate their spatial arrangement, alignment and motility. The mechanisms of fluid transport have been studied extensively at the level of an individual cilium, collectively moving metachronal waves and, more generally, the hydrodynamics of active matter. However, the connection between local cilia architecture and the topology of the flows they generate remains largely unexplored. Here, we image the mouse airway from subcellular (nm) to organ (mm) scales, characterizing quantitatively its ciliary arrangement and the generated flows. Locally, we measure heterogeneity in both cilia organization and flow structure, but, across the trachea, fluid transport is coherent. To examine this result, a hydrodynamic model was developed for a systematic exploration of different tissue architectures. Surprisingly, we find that disorder enhances particle clearance, whether it originates from fluctuations, heterogeneity in multiciliated cell arrangement or ciliary misalignment. This resembles elements of ‘stochastic resonance’, in the sense that noise can improve the function of the system. Taken together, our results shed light on how the microstructure of an active carpet determines its emergent dynamics. Furthermore, this work is also directly applicable to human airway pathologies, which are the third leading cause of deaths worldwide.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Code availability
The computer codes used in this paper are available from the corresponding author upon reasonable request.
References
Fahy, J. V. & Dickey, B. F. Airway mucus function and dysfunction. New Engl. J. Med. 363, 2233–2247 (2010).
Plasschaert, L. W. et al. A single-cell atlas of the airway epithelium reveals the CFTR-rich pulmonary ionocyte. Nature 560, 377–381 (2018).
Vladar, E. K., Bayly, R. D., Sangoram, A. M., Scott, M. P. & Axelrod, J. D. Microtubules enable the planar cell polarity of airway cilia. Curr. Biol. 22, 2203–2212 (2012).
Marshall, W. F. & Kintner, C. Cilia orientation and the fluid mechanics of development. Curr. Opin. Cell Biol. 20, 48–52 (2008).
Francis, R. J. B. et al. Initiation and maturation of cilia-generated flow in newborn and postnatal mouse airway. Am. J. Physiol. Lung Cell. Mol. Physiol. 296, L1067–L1075 (2009).
Holley, M. C. & Afzelius, B. A. Alignment of cilia in immotile-cilia syndrome. Tissue Cell 18, 521–529 (1986).
Nanjundappa, R. et al. Regulation of cilia abundance in multiciliated cells. eLife 8, e44039 (2019).
Sleigh, M. A., Blake, J. R. & Liron, N. The propulsion of mucus by cilia. Am. Rev. Resp. Dis. 137, 726–741 (1988).
Chilvers, M. A. & O’Callaghan, C. Analysis of ciliary beat pattern and beat frequency using digital high speed imaging: comparison with the photomultiplier and photodiode methods. Thorax 55, 314–317 (2000).
Shinohara, K. et al. Absence of radial spokes in mouse node cilia is required for rotational movement but confers ultrastructural instability as a trade-off. Dev. Cell 35, 236–246 (2015).
Herawati, E. et al. Multiciliated cell basal bodies align in stereotypical patterns coordinated by the apical cytoskeleton. J. Cell Biol. 214, 571–586 (2016).
Mitchell, B., Jacobs, R., Li, J., Chien, S. & Kintner, C. A positive feedback mechanism governs the polarity and motion of motile cilia. Nature 447, 97–101 (2007).
Liron, N. Fluid transport by cilia between parallel plates. J. Fluid Mech. 86, 705–726 (1978).
Bruot, N. & Cicuta, P. Realizing the physics of motile cilia synchronization with driven colloids. Ann. Rev. Condens. Matter Phys. 7, 323–348 (2016).
Brennen, C. & Winet, H. Fluid mechanics of propulsion by cilia and flagella. Ann. Rev. Fluid Mech. 9, 339–398 (1977).
Eloy, C. & Lauga, E. Kinematics of the most efficient cilium. Phys. Rev. Lett. 109, 038101 (2012).
Vilfan, A. & Jülicher, F. Hydrodynamic flow patterns and synchronization of beating cilia. Phys. Rev. Lett. 96, 058102 (2006).
Brumley, D. R., Polin, M., Pedley, T. J. & Goldstein, R. E. Hydrodynamic synchronization and metachronal waves on the surface of the colonial alga Volvox carteri. Phys. Rev. Lett. 109, 268102 (2012).
Elgeti, J. & Gompper, G. Emergence of metachronal waves in cilia arrays. Proc. Natl Acad. Sci. USA 110, 4470–4475 (2013).
Guo, H., Nawroth, J., Ding, Y. & Kanso, E. Cilia beating patterns are not hydrodynamically optimal. Phys. Fluids 26, 091901 (2014).
Feriani, L. et al. Assessing the collective dynamics of motile cilia in cultures of human airway cells by multiscale DDM. Biophys. J. 113, 109–119 (2017).
Ding, Y., Nawroth, J. C., McFall-Ngai, M. J. & Kanso, E. Mixing and transport by ciliary carpets: a numerical study. J. Fluid Mech. 743, 124–140 (2014).
McDonnell, M. D. & Abbott, D. What is stochastic resonance? Definitions, misconceptions, debates and its relevance to biology. PLoS Comput. Biol. 5, e1000348 (2009).
Sagués, F., Sancho, J. M. & García-Ojalvo, J. Spatiotemporal order out of noise. Rev. Mod. Phys. 79, 829 (2007).
Gammaitoni, L., Hänggi, P., Jung, P. & Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 70, 223–287 (1998).
Faubel, R., Westendorf, C., Bodenschatz, E. & Eichele, G. Cilia-based flow network in the brain ventricles. Science 353, 176–178 (2016).
Nawroth, J. C. et al. Motile cilia create fluid-mechanical microhabitats for the active recruitment of the host microbiome. Proc. Natl Acad. Sci. USA 114, 9510–9516 (2017).
Gilpin, W., Prakash, V. N. & Prakash, M. Vortex arrays and ciliary tangles underlie the feeding-swimming trade-off in starfish larvae. Nat. Phys 13, 380–386 (2017).
Mathijssen, A. J. T. M., Guzmán-Lastra, F., Kaiser, A. & Löwen, H. Nutrient transport driven by microbial active carpets. Phys. Rev. Lett. 121, 248101 (2018).
Rayner, C. F. et al. Ciliary disorientation alone as a cause of primary ciliary dyskinesia syndrome. Am. J. Resp. Crit. Care Med. 153, 1123–1129 (1996).
Armengot, M. et al. Nasal mucociliary transport and ciliary ultrastructure in cystic fibrosis. A comparative study with healthy volunteers. Int. J. Pediatric Otorhinolaryngol. 40, 27–34 (1997).
Bangs, F. K., Schrode, N., Hadjantonakis, A.-K. & Anderson, K. V. Lineage specificity of primary cilia in the mouse embryo. Nat. Cell Biol. 17, 113–122 (2015).
Mori, N. & Chang, K.-A. Introduction to mpiv (2003); http://www.oceanwave.jp/softwares/mpiv
Mathijssen, A. J. T. M., Doostmohammadi, A., Yeomans, J. M. & Shendruk, T. N. Hydrodynamics of microswimmers in films. J. Fluid Mech. 806, 35–70 (2016).
Lighthill, M. J. On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Math. 5, 109–118 (1952).
Blake, J. R. A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46, 199–208 (1971).
Lauga, E. & Powers, T. R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601 (2009).
Prosperetti, A. & Tryggvason, G. Computational Methods for Multiphase Flow (Cambridge Univ. Press, 2009).
Lai, S. K., Wang, Y.-Y., Wirtz, D. & Hanes, J. Micro- and macrorheology of mucus. Adv. Drug Del. Rev. 61, 86–100 (2009).
Bakunin, O. G. Reconstruction of streamline topology and percolation models of turbulent transport. Phys. Usp. 56, 243 (2013).
Goto, S. & Vassilicos, J. Particle pair diffusion and persistent streamline topology in two-dimensional turbulence. New J. Phys. 6, 65 (2004).
Subramanian, G. & Koch, D. L. Centrifugal forces alter streamline topology and greatly enhance the rate of heat and mass transfer from neutrally buoyant particles to a shear flow. Phys. Rev. Lett. 96, 134503 (2006).
Krishnamurthy, D. & Subramanian, G. Heat or mass transport from drops in shearing flows. Part 2. Inertial effects on transport. J. Fluid Mech. 850, 484–524 (2018).
Thornton, D. J., Rousseau, K. & McGuckin, M. A. Structure and function of the polymeric mucins in airways mucus. Annu. Rev. Physiol. 70, 459–486 (2008).
Bird, R. B., Armstrong, R. C. & Hassager, O. Dynamics of Polymeric Liquids. Vol. 1: Fluid Mechanics (Wiley, 1987).
Lai, M. C. & Ibrahim, A. L. Scanning and transmission electron microscopy of normal chicken tracheal epithelia. Poultry Sci. 63, 1425–1431 (1984).
Bemis, D. A. & Kennedy, J. R. An improved system for studying the effect of Bordetella bronchiseptica on the ciliary activity of canine tracheal epithelial cells. J. Infect. Dis. 144, 349–357 (1981).
ShikKim, W. et al. Tracheal reconstruction with a free vascularized myofascial flap: preclinical investigation in a porcine model to human clinical application. Sci. Rep. 7, 10022 (2017).
McDowell, E. M., Barrett, L. A., Glavin, F., Harris, C. & Trump, B. F. The respiratory epithelium. I. Human bronchus. J. Natl Cancer Inst. 61, 539–549 (1978).
Leigh, M. et al. Postnatal development of tracheal surface epithelium and submucosal glands in the ferret. Exp. Lung Res. 10, 153–169 (1986).
Yu, S. M. & Lin, K. H. Scanning electron microscopy of capsaicin-pretreated trachea in the rat during postnatal development. Histol. Histopathol. 10, 853–860 (1995).
Pastor, L. M. A morphological study of the tracheal epithelium of the snake Natrix maura. J. Anatomy 172, 47–57 (1990).
Sanderson, M. & Sleigh, M. Ciliary activity of cultured rabbit tracheal epithelium: beat pattern and metachrony. J. Cell Sci. 47, 331–347 (1981).
Satir, P. & Dirksen, E. R. Function–Structure Correlations in Cilia from Mammalian Respiratory Tract 473–494 (American Cancer Society, 2011).
Acknowledgements
This work was supported by funding from the National Science Foundation Center for Cellular Construction (NSF grant no. DBI-1548297), a Human Frontier Science Program Fellowship to A.J.T.M.M. (LT001670/2017) and a Ruth L. Kirschstein National Research Service Award to M.H. (F32HD089639). M.P. acknowledges support from the Keck Foundation. We thank K. Anderson (Sloan Kettering Institute) for providing the Arl13b-mCherry/Centrin-GFP animals used for this study and the Stanford Research Computing Center for providing computational resources and support. We thank W. Gilpin for providing comments on the manuscript.
Author information
Authors and Affiliations
Contributions
G.R.R.-S.J., W.M. and M.P. designed the research. G.R.R.-S.J. and M.H. performed the tissue imaging. G.R.R.-S.J. analysed the data. A.J.T.M.M. contributed intellectually to the paper and developed the simulations. G.R.R.-S.J. and A.J.T.M.M. wrote the manuscript. M.H. and L.J. provided key reagents and resources for tissue imaging. All authors edited the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Quantification of spatial patterning in airway ciliary arrays.
A. Immunofluorescence image of a trachea expressing Centrin-GFP (left). Regions outlined by the squares are magnified to the right, showing that multiciliated cells form a ‘patchwork’ pattern in the distal (1), medial (2) and proximal (3) regions of the trachea. B. Illustration of cilia orientation analysis. Individual cilia orientation is measured from pairs of Centrin and Centriolin images. First, individual basal bodies (crossed symbols) are identified from Centrin images. Then the cross-correlation function for a pair of Centrin-Centriolin images is calculated in windows of 50 pixels centered around each basal body. The direction of maximum correlation corresponds to the orientation of each cilium (white arrows). C. Heatmap scaled such the 1 corresponds to the regions of maximum cilia activity in Supp. Video 1. Right: Binary image where white regions show regions where cilia are active in Supp. Video 1 (See Methods §2 b). D. Coverage fraction and wavelength measured by calculating the spatial correlation function of binary images where regions with cilia activity were identified (e.g. image shown in C).
Extended Data Fig. 2 Quantification of flows generated by airway ciliary arrays.
A. Transmitted light image of trachea showing the scale at which flow is measured. Right: Longitudinal flow strength (vx, red-blue) generated by trachea pictured left. Entire flow strength and streamlines shown in (Fig. 2A,C). B. Representative transmitted light image of a typical region of the tissue where flow microstructure is analysed. Right: Longitudinal flow strength (vx, red-blue) generated by trachea pictured left. Entire flow strength and streamlines shown in (Fig. 2A,C; right). C. Quantification of beat frequency and tip velocity of cilia in multiciliated cells. Kymographs drawn from the lines shown in DIC image. Each peak corresponds to one cilia beat cycle (blue), while the slopes of the line indicate the rate at which cilia tips move over time (green). Boxplot central marks indicate the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers. D. Plot of temporal correlations of the flow field. Plot on the right shows the region where the δCvv(τ) decays, magnified. Each trace is the correlation function M9calculated for a field of view of the size shown in B. Points correspond to values measured, solid line shows exponential fits with an oscillatory component (See Methods §2 d). E. Plot of spatial correlations of flow fields measured experimentally. Points correspond to values calculated, solid lines show fits (See Methods §2 d). Right: Heatmap of the two dimensional spatial autocorrelation function \({C}_{vv}(\bf{R})\) for the flow field shown in Fig. 2C (right panel). F. Plot of spatial correlations of simulated flow fields. Measurements of multiciliated cell organisation were used as an input for these simulations (See Methods §3 e). Right: Heatmap of the two dimensional spatial autocorrelation function \({C}_{vv}(\bf{R})\) for the simulated flow field shown in Fig. 2D (right panel).
Extended Data Fig. 3 Effect of confinement on Stokeslet flow in a liquid film.
Shown is the analytical solution using 9 image reflections, (n) = (0) − (9) in Table 1 of Mathijssen et al. [34]. The film height in the z direction is H, compared to the horizontal scale x, y ∈ [− 1, 1]. The Stokeslets are located in the middle of the film, at z = H/2, and oriented in the x direction (white arrows). Top panels: Magnitude (thermal) and streamlines (black arrows) of the flow velocity. Bottom panels: Same, showing the x component (red-blue) of the flow. For thin films a recirculation emerges, with a vortex centre marked in green.
Extended Data Fig. 4 Three-dimensional structure of the flow generated by a ciliary array.
Three-dimensional structure of the flow generated by a ciliary array, simulated for a square lattice with coverage fraction ϕ = 0.1, patchiness λ/H = 12.8, crystallinity γ = 1 and aligned cilia 〈px〉 = 1. The wavelength λ = L = 128μm and the film height H = 10μm. Shown are streamlines (white) and the longitudinal flow strength (red-blue). Left. Top view showing the z-averaged flow velocity, \(\bar{\bf{v}}\), which is the same as Fig. 3D4. Upper right. Cross-section at y = 0 or y = L, between the ciliated cells. Lower right. Cross-section at y = L/2, above the ciliated cells.
Extended Data Fig. 5 Effect of shear-dependent viscosity on particle clearance.
A. Non-Newtonian viscosity μ as a function of shear rate \(\dot{\gamma }\) in a power-law fluid (Eq. M19), for a shear-thinning liquid (blue, n = 0.5), a Newtonian liquid (green, n = 1) and a shear-thickening liquid (red, n = 2). B. Channel flow velocity profiles for a power-law fluid. Symbols indicate simulated flows with the CFD solver and lines show the theoretical prediction. For a shear-thinning fluid (blue) the profile is flatter, for a shear-thickening fluid it is sharper (red), and for a Newtonian liquid we recover a parabolic Poiseuille flow. C. Flow generated by a ciliary array for different values of the power-law exponent, n, simulated for a square lattice with coverage fraction ϕ = 0.1, patchiness λ/H = 12.8, crystallinity γ = 1 and aligned cilia 〈px〉 = 1. Shown are streamlines (white) and the longitudinal flow strength \({\bar{v}}_{x}\) normalised with respect to the mean flow \(\langle {\bar{v}}_{x}\rangle\) of a Newtonian fluid (red-blue), as in Fig. 3D4. D. Plot of total flux and clearance time for a shear-thinning (blue) and a shear-thickening fluid (red) as a function of patchiness, normalised with respect to the case of homogeneous coverage (λ = 0). E. Plot of total flux and clearance time for a shear-thinning (blue) and a shear-thickening fluid (red) as a function of Péclet number, normalised with respect to the case of weak noise (Pé = 10−4).
Extended Data Fig. 6 Total flux and particle clearance for a hexagonal array of ciliary patches.
The lattice is shown in the inset of panel D, where red indicates a multiciliated cell. A. Simulated flow for cilia oriented in the \(\hat{\bf{x}}\) direction. Shown are streamlines (white) and the longitudinal flow strength (red-blue). The coverage fraction is ϕ = 0.33, the patchiness is λ/H = 12.8, the crystallinity γ = 1 and the cilia are all aligned 〈px〉 = 1. B. Same, for cilia oriented in the θ = π/6 direction. C. Same, for cilia oriented in the \(\hat{\bf{y}}\) direction. D. Plot of total flux (blue) and clearance time (red) as a function of patchiness, for cilia oriented in the \(\hat{\bf{y}}\) direction, similar to Fig. 3D. E. Plot of total flux (blue) and clearance time (red) as a function of Péclet number, for cilia oriented in the \(\hat{\bf{y}}\) direction, similar to Fig. 4C.
Extended Data Fig. 7 From the literature: SEM images of airway multiciliated tissue.
A. Chicken; Image adapted from46. B. Dog; Image adapted from47. C. Pig; Image adapted from48. D. Human; Image adapted from49. E. Ferret; Image adapted from50. F. Rat; Image adapted from51. G. Snake; Scale bar=100 μm. Image adapted from52. H. Rabbit; Image adapted from53. I. Hamster; Image adapted from54. Scale bar=10 μm for all panels except G.
Supplementary information
Supplementary Information
Extended materials and methods.
Supplementary Video 1
Activity of a field of multiciliated cells in the trachea. Time-lapse ex-vivo DIC imaging of a section of the mouse trachea multiciliated tissue.
Supplementary Video 2
Ciliary driven flows are globally coherent. Flow generated by multiciliated cells across the entire trachea. Flow is imaged by time-lapse confocal microscopy. Fluorescent beads serve as tracer particles.
Supplementary Video 3
Ciliary driven flows are locally heterogeneous. Microstructure of the flow generated by a subsection of the trachea multiciliated tissue. Flow is imaged by time-lapse confocal microscopy. Fluorescent beads serve as tracer particles.
Supplementary Video 4
Activity of multiciliated cells in the trachea.Time-lapse ex-vivo DIC imaging of a cross-section of the mouse trachea multiciliated tissue.
Supplementary Video 5
Fluctuations improve particle clearance in patchy arrangements of multiciliated cells. Particle trajectories (Np = 1,000) are simulated for a range of noise strengths. Initially, the particles are distributed evenly and identically in all three panels, emulating a uniform deposition from breathed-in air. Over time, they are subject to flow (same as in Fig. 4c) and fluctuations with different diffusion constants, such that the Péclet number is Pé = 104, 103, 102, respectively. Colours indicate particle index and black trails show their pathlines. For weak noise the particles accumulate in recirculation zones, but strong fluctuations facilitate a faster clearance.
Rights and permissions
About this article
Cite this article
Ramirez-San Juan, G.R., Mathijssen, A.J.T.M., He, M. et al. Multi-scale spatial heterogeneity enhances particle clearance in airway ciliary arrays. Nat. Phys. 16, 958–964 (2020). https://doi.org/10.1038/s41567-020-0923-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0923-8
This article is cited by
-
Artificial microtubules for rapid and collective transport of magnetic microcargoes
Nature Machine Intelligence (2022)
-
A quantitative interspecies comparison of the respiratory mucociliary clearance mechanism
European Biophysics Journal (2022)
-
Active carpets drive non-equilibrium diffusion and enhanced molecular fluxes
Nature Communications (2021)
-
Helpful disorder in the lungs
Nature Physics (2020)