Abstract
The theory governing the strong nuclear force—quantum chromodynamics—predicts that at sufficiently high energy densities, hadronic nuclear matter undergoes a deconfinement transition to a new phase of quarks and gluons1. Although this has been observed in ultrarelativistic heavy-ion collisions2,3, it is currently an open question whether quark matter exists inside neutron stars4. By combining astrophysical observations and theoretical ab initio calculations in a model-independent way, we find that the inferred properties of matter in the cores of neutron stars with mass corresponding to 1.4 solar masses (M⊙) are compatible with nuclear model calculations. However, the matter in the interior of maximally massive stable neutron stars exhibits characteristics of the deconfined phase, which we interpret as evidence for the presence of quark-matter cores. For the heaviest reliably observed neutron stars5,6 with mass M ≈ 2M⊙, the presence of quark matter is found to be linked to the behaviour of the speed of sound cs in strongly interacting matter. If the conformal bound \({c}_{\rm{s}}^{2}\le 1/3\) (ref. 7) is not strongly violated, massive neutron stars are predicted to have sizable quark-matter cores. This finding has important implications for the phenomenology of neutron stars and affects the dynamics of neutron star mergers with at least one sufficiently massive participant.
Similar content being viewed by others
Main
Observations of neutron stars (NSs) inform us about the properties of matter inside their cores in an indirect way. Translating them to statements about NS matter requires the modelling of strongly interacting matter all the way from the crust to the highest densities reached inside the stars. The lack of accurate first-principles predictions at densities beyond the nuclear matter saturation (baryon number) density n0 ≈ 0.16 fm−3 has so far prevented determination of the phase of matter inside NS cores, and it is unlikely that the question will be answered based on gravitational wave (GW) data alone, at least in the near future8. Nevertheless, recent observations are beginning to offer empirical constraints so strong that a model-independent approach to the problem has become feasible.
The equation of state (EoS) of NS matter (the relation p(ϵ) between the pressure and energy density of beta-equilibrated matter interacting under quantum chromodynamics (QCD) at temperature T = 0) is known in two opposing limits. From the well-studied NS crust region9 to the density nCET ≡ 1.1n0, where matter resides in the hadronic-matter phase, modern nuclear-theory machinery, such as chiral effective field theory (CET), provides the EoS to good precision, currently better than ±24% (refs. 10,11). In the opposite limit of very high densities, perturbative-QCD (pQCD) techniques, rooted in high-energy particle phenomenology and built on deconfined quark and gluon degrees of freedom12,13, become accurate, providing the quark-matter EoS to the same accuracy at densities n ≳ 40n0 ≡ npQCD.
In the above two limits, QCD matter is known to exhibit markedly different properties. High-density quark matter is approximately scale-invariant, or conformal, whereas in hadronic matter the number of degrees of freedom is much smaller and scale invariance is also violated by the breaking of chiral symmetry. These qualitative differences are reflected in the values taken by different physical quantities. The speed of sound takes the constant value \({c}_{\rm{s}}^{2}=1/3\) in exactly conformal matter and slowly approaches this number from below in high-density quark matter12. By contrast, in hadronic matter, the quantity varies considerably: below saturation density, CET calculations indicate \({c}_{\rm{s}}^{2}\ll 1/3\), while at higher densities most hadronic models predict max\(({c}_{\rm{s}}^{2})\gtrsim 0.5\). The polytropic index \(\gamma \equiv {\rm{d}}({\mathrm{ln}}\,p)/{\rm{d}}({\mathrm{ln}}\,\epsilon )\), on the other hand, has the value γ = 1 in conformal matter, while both CET calculations and hadronic models generically predict γ ≈ 2.5 around and above saturation density. Finally, the number of degrees of freedom is reflected in the pressure normalized by that of free quark matter (the Fermi-Dirac (FD) limit), p/pFD (ref. 12). This quantity obtains values of order 0.1 in CET calculations and hadronic models, while pQCD predictions typically fall inside the range [0.5, 0.8] around n = npQCD.
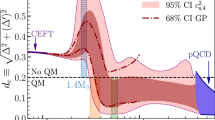
In the intermediate density range, nCET < n < npQCD, where NS cores lie, a robust model-independent approach is to introduce a set of basis functions to interpolate the EoS, thus creating an ensemble of all viable NS-matter EoSs14,15,16,17. To remove possible bias originating from the choice of basis functions, we have used multiple interpolation methods, finding consistent EoS and NS mass–radius (MR) regions, as reviewed in the Methods (and shown in Extended Data Fig. 1). Given this agreement, in the following we present results from a new ‘speed-of-sound’ interpolation method we have developed here, which has the added benefit of keeping track of the stiffness of the EoS and allows for arbitrarily strong crossover transitions, tantamount to discontinuous first-order transitions. We impose the following two robust astrophysical constraints on the EoS: the requirement of supporting a 1.97M⊙ NS (refs. 5,6) and that the tidal deformability Λ for a 1.4M⊙ star obeys 70 < Λ(1.4M⊙) < 580 (refs. 18,19). In total, we analysed ~570,000 EoSs (displayed in Fig. 1), to which we apply a mild smoothness condition in some individual analyses, as discussed in the Methods (and shown in Extended Data Fig. 2).
The bands have been generated by superimposing large numbers of individual EoSs generated with the speed-of-sound interpolation method introduced in this paper. The colour coding refers to the maximal value that the speed of sound squared \({c}_{\rm{s}}^{2}\) reaches at any density. For comparison, the black lines stand for the different hadronic EoSs we have obtained from refs. 9,20,21. Finally, the light blue regions correspond to the CET and pQCD EoSs of refs. 12,14, and the rough location of the deconfinement transition in hot quark-gluon plasma, ϵQGP, is indicated for illustrative purposes.
Having the ensemble of interpolated EoSs at our disposal, we can determine the allowed behaviours of different physical quantities. Figure 2a presents a three-dimensional (3D) rendering in which a representative sample of our EoSs is represented by thin black lines, all starting from a region characterized by the CET EoS and ending in a pQCD one. For comparison, we also include a large set of nuclear matter EoSs (thick black lines), corresponding to the hadronic EoSs of Fig. 1, obtained from refs. 9,20,21, of which we have discarded those incompatible with our observational constraints. The interpolated EoSs follow a non-trivial trajectory: at low densities, they follow a trend set by the nuclear EoSs but later deviate from it, signalling a change in the underlying physics. This transition corresponds to the change of (the logarithmic) slope of p(ϵ) visible around ϵc ≈ 400−700 MeV fm−3 in Fig. 1, which roughly coincides with the energy density inside free nucleons and with the location of the deconfinement transition at high temperatures22,23. At even higher densities, the interpolated EoSs approach the pQCD predictions for \({c}_{\rm{s}}^{2}\), p/pFD and γ (ref. 12).
a, A 3D rendering of trajectories of a representative subset of interpolated (thin black lines) and hadronic (thick black lines) EoSs in a space spanned by the polytropic index γ, the pressure ratio p/pFD and the squared speed of sound \({c}_{\rm{s}}^{2}\). The solid blue and empty cyan diamonds mark the centres of 1.4M⊙ NSs, and the solid red and empty magenta circles denote the same for \({M}_{\max }\) stars. The thick light blue line denotes the region of the 3D space spanned by the high-density pQCD EoS, and the region occupied by low-density matter is indicated by the label ‘Nucl’. b,c, Projection of the 3D image to the p/pFD–γ (b) and \({c}_{\rm{s}}^{2}\)–γ (c) planes. In c, the light blue star indicates the high-density conformal pQCD limit. An animation of the figure is available as Supplementary Video 1.
On each of the EoS lines in Fig. 2a, the density reached in the centres of 1.4M⊙ NSs is marked with solid blue (interpolated EoSs) or empty cyan (nuclear EoSs) diamonds. The significant overlap between the two distributions shows that the material properties inside 1.4M⊙ stars are consistent with a description in terms of hadronic degrees of freedom. However, the same is not true for the majority of maximally massive stars (filled red and empty magenta circles), for which the two families of points are clearly separated in Fig. 2 (see Fig. 2b,c for two 2D projections of the 3D plot). This discrepancy shows that the material properties in the centres of the largest NSs are not consistent with the presence of hadronic matter except for a small number of EoSs with very large values of \({c}_{\rm{s}}^{2}\). As demonstrated in Extended Data Fig. 3, the vast majority of these points lie to the right of the kink on the EoS band, confirming the likely existence of quark cores inside the \({M}_{\max }\) stars.
To make the above observations somewhat more quantitative, it would clearly be valuable to establish a connection between the physical phase of QCD matter and its EoS. To this end, we note that our results from Fig. 2 and the distinct values the polytropic index obtains in nuclear and quark matter calculations both suggest using the values of γ as a good approximate criterion. Given that γ = 1.75 is both the average between its pQCD and CET limits and very close to the minimal value the quantity obtains in viable hadronic models (see Fig. 2 and our discussion in the Methods), we are led to choose the following criterion for separating hadronic from quark matter: given an interpolated EoS, the smallest density from which γ is continuously less than 1.75 to asymptotic densities is identified with the onset of quark matter. We emphasize, however, that this is only an approximate rule to guide our analysis, and not a robust or rigorous result.
As a first application of the above criterion, for NSs with M = 1.4M⊙ we find that the central polytropic index always satisfies γ ≳ 2, implying that the stars are composed of hadronic matter as expected. In contrast, maximally massive stars have γ values much closer to unity, indicating that they typically contain quark matter. In Fig. 3, we display the sizes of quark cores in the latter NSs. The core has a significant extent, \({M}_{{\rm{core}}}>0.25{M}_{\odot }\), for all those EoSs that satisfy \({c}_{\rm{s}}^{2}<0.5\). However, for extreme EoSs in which the speed of sound almost reaches that of light, the core may be significantly smaller or even absent. Note that this is consistent with the fuller picture given by Fig. 2, mentioned above.
Predictions for the radius and the mass of the quark cores in maximally massive NSs are displayed. The maximal value that the speed of sound squared \({c}_{\rm{s}}^{2}\) reaches in each individual EoS is indicated by the colour coding of the corresponding point. Points corresponding to lower \({c}_{\rm{s}}^{2}\) values are drawn on top of those corresponding to higher ones. The NS in the inset visualizes a 12 km, 2M⊙ star with a 6.5 km quark core, built with a subconformal (\({c}_{\rm{s}}^{2}<1/3\)) EoS.
If the maximal value of \({c}_{\rm{s}}^{2}\) exceeds 0.7, we find a small class of EoSs where even maximally massive stars do not contain quark cores according to our criterion. We find that each of these EoSs exhibits an interval in ϵ where γ < 0.5, which destabilizes the star. This corresponds to a rapid change in the EoS, and is practically indistinguishable from a first-order phase transition. The minimal latent heat (that is, the extent of the interval with γ < 0.5) required for the destabilization is (Δϵ)lat > 130 MeV fm−3, corresponding to a relative discontinuity of (Δϵ)lat/ϵ > 0.2 at the beginning of the transition. We thus find that for all stable NSs to be composed of hadronic matter alone, the EoS must both significantly violate the conformal limit and feature a sufficiently strong phase transition. Finally, two-solar-mass stars contain a quark core for all EoSs that satisfy \({c}_{\rm{s}}^{2}<0.4\), irrespective of the properties of the phase transition; for subconformal EoSs, featuring \({c}_{\rm{s}}^{2}<1/3\) at all densities, the radius of the core R ≈ 6.5 km is roughly half of the entire star’s radius. By contrast, if the EoS supports substantially higher maximal masses \({M}_{\max }>2.25{M}_{\odot }\), quark cores are absent in 2M⊙ stars (Extended Data Fig. 4).
In conclusion, our model-independent analysis has demonstrated that the existence of quark cores in massive NSs should be considered the standard scenario, not an exotic alternative. For all stars to be made up of hadronic matter, the EoS of dense QCD matter must be truly extreme. This view is also consistent with recent NS radius measurements, which are compatible with the larger radii predicted by the less extreme EoSs (see discussion in the Methods and Extended Data Fig. 5). Note, however, that our analysis does not preclude the possibility of massive, purely hadronic stars, even with less extreme EoSs, as quark cores may appear only at very high masses, even beyond 2M⊙. Nuclear-matter EoSs that predict purely hadronic 2M⊙ stars (for example, refs. 24,25,26,27,28) may therefore be compatible with our results until very high densities.
The existence of quark cores in at least some NSs and the fact that the nucleation of quark matter begins so close to the maximum-mass limit may have very interesting observable consequences. In NS mergers, the core may lead to shock waves reflecting from the quark–hadron interface inside hypermassive NSs. This may be particularly amplified if the conformal limit is strongly violated in hadronic matter, leading to large differences in the speeds of sound between the phases. In addition, the onset of the transition may give rise to dissipation during the merger in the form of a large effective bulk viscosity that may lead to an enhanced damping of the ringdown. Importantly, both of these have the potential to lead to observable effects in GW signals from NS mergers and the associated electromagnetic counterparts.
Finally, our results are systematically improvable with more observations. For example, there are several candidates for NSs with very large masses (see, for example, ref. 29). If even one of these stars turns out to have a mass significantly larger than 2M⊙, this would impose strong new constraints on the EoS and for example imply that the conformal bound must be broken. Similarly, with many binary-NS merger observations currently recorded by LIGO/Virgo, the current limits on tidal deformability will inevitably become tighter, enabling additional improvements to our analysis. With these advances and the road map laid out in our work, further significant progress in understanding the nature of ultra-dense matter inside NSs can be expected in the near future.
Methods
New speed-of-sound interpolation
The starting point of the new interpolation method is to consider the squared speed of sound \({c}_{\rm{s}}^{2}\) as a function of the baryon chemical potential μ, and use this quantity to construct all other thermodynamic functions, in particular the pressure p(μ). In practice, the speed of sound is first integrated from the CET matching point nCET = 1.1n0 to higher densities to give the baryon density
where μCET is the baryon chemical potential corresponding to the density nCET, that is, nCET ≡ n(μCET). This result is then further integrated to arrive at the pressure:
where pCET ≡ p(μCET).
The above relations must be solved numerically in general, but in the following simple case that we have implemented in our analysis, they may be dealt with analytically. Namely, we first take the sequence of Np pairs
with μ1 = μCET, \({\mu }_{{N}_{p}}=2.6\) GeV and μi − 1 < μi < μi + 1 for all other i. We then construct a \({c}_{\rm{s}}^{2}\) curve as a piecewise-linear function connecting these points; that is, for each i = 1, …, Np − 1 and for μ ∈ [μi, μi + 1]
At the matching points μ1 and \({\mu }_{{N}_{p}}\), we require p and \({c}_{\rm{s}}^{2}\) to match the corresponding values given by the CET and pQCD EoSs, respectively. In addition, we take n to be continuous at each matching point, but note that our construction allows for EoSs that mimic discontinuous first-order transitions arbitrarily closely.
For a given Np, we have Np − 2 independent matching chemical potentials μi and Np − 2 independent speed-of-sound points \({{c}_{{\rm{s}},i}^{2}}\), from which one of both is determined through matching to the high-density EoS, leaving 2Np − 6 parameters for given low- and high-density EoSs. If we instead write this in terms of the number of interpolating segments N ≡ Np − 1, then the result becomes 2N − 4. This is one free parameter fewer than the number of free parameters needed to define a polytropic EoS composed of the same number of segments16.
The above procedure is used to construct individual EoSs by choosing N = 3, 4, 5 and then randomly picking values for the matching points μi, speeds of sound cs,i and the pQCD parameter XpQCD (ref. 38). The parameter values are taken from uniform distributions μi ∈ [μCET, 2.6 GeV], \({{c}_{{\rm{s}},i}^{2}}\in (0,1)\), XpQCD ∈ [1, 4], in addition to which we choose roughly the same number of the ‘hard’ or ‘soft’ nuclear EoSs of ref. 14. Finally, we vary the extreme EoSs in the ϵ–p plane within each \({c}_{\rm{s}}^{2}\) band plotted in our paper, to ensure that we satisfactorily probe the size of these regions. This leads to the ensemble studied above, which consists of ~570,000 individual EoSs. Roughly 160,000 of these fulfil the astrophysical constraints described in the main text, while ~70,000 of the allowed EoSs contain at least one first-order phase transition. We have carefully made sure that these ensemble sizes are sufficiently high that our results are stable with respect to increasing the number of EoSs.
Finally, we note that while the interpolation method described above is genuinely new, a number of related articles have recently appeared in which the NS matter EoS has been constructed starting from the speed of sound39,40,41,42,43,44. Although most of these works introduce a non-trivial ansatz function for the quantity, thus being more restrictive than our approach, in ref. 39 the speed of sound is allowed to behave in a more general way. The main difference between the EoS bands constructed in this reference and our current work originates from our high-density pQCD constraint, which effectively forces the EoS to be softer at high densities.
Comparison of different interpolations
To quantify the potential bias introduced into our results by the selection of the speed-of-sound interpolation method, we compare our EoS and MR ensembles to ones obtained with the following two schemes:
-
a piecewise polytropic interpolation of the pressure as a function of baryon density, \({p}_{i}(n)={\kappa }_{i}{n}^{{\varGamma }_{i}}\)
-
a spectral interpolation of the adiabatic index \(\varGamma (p)=\frac{\epsilon (p)+p}{p}{\left[\frac{{\rm{d}}\epsilon }{{\rm{d}}p}\right]}^{-1}\) in terms of Chebyshev polynomials
Both of these interpolation methods have been abundantly discussed in the literature14,15,16,17,19,45,46.
We construct the EoS bands corresponding to each of the three interpolation methods, implementing the astrophysical constraints listed in the main text. To make the EoS families comparable to each other, we not only make sure that the ensembles are of roughly similar size, but in addition choose the numbers of free parameters in the EoSs to be approximately equal. For the piecewise polytropic interpolation, we allow up to four independent segments16 (amounting to five free parameters), while for the spectral interpolation proposed by Lindblom45 we use Chebyshev polynomials of degree five (four free parameters). Finally, for the speed-of-sound interpolation, we use up to five independent segments (six free parameters) in this comparison. In each case, we randomly generate large ensembles of interpolation functions, ensure that the resulting EoSs are causal and thermodynamically consistent, and finally discard those EoSs that are in disagreement with the observational constraints introduced in the main text. Again, we add no explicit first-order transitions to the EoSs, but allow continuous transitions that are arbitrarily strong, thus closely mimicking discontinuous phase transitions.
Our conclusion from the comparison of the constructed EoSs (Extended Data Fig. 1a) is that the speed-of-sound and polytropic interpolations produce nearly identical results, while the spectral interpolation leads to a somewhat more constrained band. This is not surprising; the spectral method does not build on piecewise-defined interpolating functions, so the resulting EoSs are smooth by construction and unable to describe very sharp and rapid changes in the EoSs.
The families of MR curves obtained by integrating the Tolman–Oppenheimer–Volkoff equations using the above three ensembles of EoSs also largely indicate agreement between the methods (Extended Data Fig. 1b). The minimal and maximal radii for a fixed mass agree well among the different interpolations, with the spectral interpolation occupying a slightly more restricted area for low-mass stars with M < 1.2M⊙. The agreement between different interpolations also persists as a function of tidal deformability: constraining Λ(1.4M⊙) according to 70 < Λ(1.4M⊙) < 580 (ref. 19), we find that the different interpolations still give similar maximal radii as functions of the NS mass as long as M ≳ 1.4M⊙. In particular, the maximal radii at M = 1.4M⊙ are in excellent quantitative agreement among the different interpolation methods, as is expected from the previously observed tight correlation between NS radii and tidal deformabilities16. Considering stars with smaller masses, we observe that the speed-of-sound and piecewise polytropic interpolations allow EoSs that are extremely hard at low densities, leading to large radii R ≈ 14 km for M ≈ M⊙, but rapidly soften at larger densities, such that for M = 1.4M⊙ the radii are smaller and consistent with the upper limits for tidal deformability. Again, because the spectral method leads to smoother interpolations, it is natural that it does not allow these rapidly changing EoSs.
Another difference between the interpolation schemes is that the polytropic interpolation does not allow for as massive stars as the other two. We attribute this to the fact that to achieve very large maximal masses, the EoS needs to stay very stiff, cs ≈ 1, throughout an extensive density window, which is difficult to realize with polytropic interpolation functions. This difference between different interpolations is somewhat ameliorated when upper limits are placed on the tidal deformability.
Polytropic index and its relation to the phase of QCD matter
As stated in the main text, our criterion for identifying the phase of QCD matter in NS cores is based on analysing the behaviour of the polytropic index \(\gamma \equiv {\rm{d}}({\mathrm{ln}}\,p)/{\rm{d}}({\mathrm{ln}}\,\epsilon )\), that is, the slope of the EoS in Fig. 1 and Extended Data Figs. 1a, 2 and 3. Here, we comment on the physics behind this statement, and explain our choice to identify the presence of quark matter using as the quantitative criterion γ < 1.75 continuously up to asymptotic densities.
Matter that exhibits exact conformal symmetry, that is, it does not possess intrinsic mass scales, is characterized by γ = 1, independent of the strength of the coupling. This is so because, in the absence of any dimensionful parameters, the energy density and pressure must be proportional to each other, leading to γ = 1. This symmetry can also be shown to lead to a speed of sound squared of \({c}_{\rm{s}}^{2}=1/3\) for the system.
In low- and moderate-density QCD matter, it is well known that the ground state does not exhibit the approximate chiral symmetry of the underlying Lagrangian (see, for example, ref. 47 for details). This spontaneous breaking of the symmetry leads to the emergence of the fundamental scales of nuclear matter, such as hadron masses, and scale-dependent interactions. These mass scales lead to a highly non-conformal behaviour for the EoS, which is reflected in the polytropic index taking large values, typically in excess of 2, in viable models of high-density nuclear matter.
Collections of γ values predicted by different nuclear physics models are available through the related adiabatic index \(\varGamma =\frac{\epsilon +p}{\epsilon }\ \gamma\), tabulated for example in table III of ref. 48 and plotted in fig. 5.9 of ref. 49. A closer inspection of the wide class of EoSs we have gathered from refs. 9,20,21 shows that, although there are a number of EoSs for which the polytropic index reaches values of order 1.5 or below, all of these are in conflict with the recent LIGO/Virgo tidal deformability bound—a constraint that in particular rules out typical hyperonic EoSs. For the viable hadronic EoSs we have analysed, γ stays around or above 1.75 in all cases except for MPA1, for which the parameter can drop to ~1.6 at very high densities. This EoS, however, exhibits a speed of sound squared extremely close to unity exactly when γ falls below 2. In addition to casting doubt on its reliability, this fact highlights the lack of overlap between its high-density behaviour and that of our family of interpolated EoSs.
In high-density quark matter, on the other hand, the underlying approximate chiral symmetry of QCD is restored and, as a result, the system exhibits approximate conformal symmetry. Minor violations of conformal behaviour arise from the masses of the up, down and strange quarks; these are, however, very small compared to the nucleon masses. Moreover, the interactions between quarks and gluons also lead to a mild breaking of conformal symmetry in the quark-matter phase, manifesting as a logarithmic dependence of the strong coupling constant on the baryon chemical potential. To a good accuracy, however, quark matter always behaves as an ultrarelativistic gas of interacting quarks and gluons, which becomes even more pronounced in the controlled, perturbative high-density region of the QCD phase diagram, where the polytropic index γ quickly approaches unity.
In the most non-trivial density range near the deconfinement transition, QCD matter evolves from the highly non-conformal hadronic behaviour to one characteristic of quark matter. This transition may take place either as a discontinuous jump in energy density, in which case the value γ = 1.75 may never be reached, or in a smooth crossover manner, whereby a crisp phase identification may not always be feasible (then there may even exist an overlap region where the system can be described both in terms of nuclear and quark degrees of freedom). In either case, our results indicate that the cores of typical pulsars and maximal-mass NSs very probably do not reside here, but rather safely belong to the nuclear and quark matter regimes, respectively. This is reflected in the fact that our qualitative conclusions are not sensitive to the exact choice of the critical polytropic index as long as it resides between the hadronic and quark matter regimes. Indeed, only our detailed numerical conclusions would be somewhat modified should we vary the number γ = 1.75 in a moderate way.
Analysis of EoS smoothness
In addition to reaching large speeds of sound, one way in which some of the EoSs generated by the speed-of-sound interpolation method can be classified as extreme is that the piecewise nature of the interpolation functions allows for very quick changes in the material properties of the matter in arbitrarily small density windows. Although such versatility is, in principle, a desirable feature of the interpolator, these structures are not very likely to appear in nature, and in addition bring unnecessary complications to the polytropic-index analysis performed in the main text. To quantify the level of local structure in our EoSs, we classify them according to the smallest (logarithmic) energy-density interval where structures appear. In practice, this is implemented by demanding that the energy densities at two successive inflection points, ϵi and ϵi + 1, where the speed of sound changes its behaviour, satisfy \(({\epsilon }_{i+1}-{\epsilon }_{i})/{\epsilon }_{i}>\Delta \mathrm{ln}\,\epsilon\) with a given constant \(\Delta \mathrm{ln}\,\epsilon >0\). Note that imposing this constraint does not exclude discontinuous first-order phase transitions or rapid crossovers.
As demonstrated in Extended Data Fig. 2, we find that placing minor smoothness limits (\(\Delta \mathrm{ln}\,\epsilon \lesssim 1\)) affects the allowed EoS region mainly around the matching points, where the EoS is best known, but does not have a significant effect at intermediate densities. However, somewhat larger values (\(\Delta \mathrm{ln}\,\epsilon \gtrsim 1\)) begin to significantly constrain the allowed region at all densities. This shows that the EoSs that make up the boundaries of the EoS band must exhibit both very large speeds of sounds as well as rapid changes in material properties.
For our analysis of the central values of γ in stars of different masses, we have used \(\Delta \mathrm{ln}\,\epsilon >0.5\), which has a minor effect on the global characteristics of the EoS family. In particular, this cut has a minor effect on the MR relation for stars above 1.4M⊙, shifting the extremes of the allowed radius for a given mass by ~0.3 km at most. Moreover, we note that, for completeness, we have also allowed the first inflection point to approach nCET without limit, finding that all the results presented in the main text remain unchanged.
Comparison with recent mass and radius constraints
Our ensemble of EoSs can also be transformed to the M–R plane to compare its behaviour to recent radius observations of NSs. In Extended Data Fig. 5, we overlay a few representative X-ray MR measurements on top of our family of MR curves, obtained from the EoS ensemble of Fig. 1. We show examples of measurements obtained with three different methods: direct atmosphere-model fits to the time-evolving X-ray burst spectra (corresponding to the low-mass X-ray binary (LMXB) system 4U 1702–429 (yellow curve))30, cooling-tail method fits to X-ray burst observations (LMXBs 4U 1724–307 (light brown) and SAX J1810.8–2609 (cyan))31 and quiescent LMXB spectra fits to sources with reliable distance measurements (NGC 6304 (dark brown), NGC 6397 (green), M13 (purple), M28 (orange), M30 (black), ω Cen (magenta), 47 Tuc X5 (blue) and 47 Tuc X7 (red))32,33,34,35,36,37. For the quiescent LMXB measurements we use public data from refs. 36,37. We assume, for simplicity, no hot spots. The corresponding atmospheres are assumed to be composed of either hydrogen (dotted lines) or helium (dashed lines), depending on the source.
In general, this kind of qualitative comparison remains largely inconclusive and warrants a further quantitative treatment taking into account the full interplay between different measurements and their uncertainties. That being said, we note that the measurements are consistent with the lower \({c}_{\rm{s}}^{2}\) values as the measured radii are typically around R ≈ 12 km. This is especially true for the most precise MR measurement concerning the NS in 4U 1702−429, which is fully compatible with the subconformal-EoS region, where \({c}_{\rm{s}}^{2}<1/3\). We emphasize that this particular selection of measurements presented in Extended Data Fig. 5 is by no means meant to be exhaustive. A more detailed self-consistent Bayesian treatment of the problem with all the available measurements present in the literature is left for future work.
Code availability
The code used to construct the interpolated EoSs is available from the authors upon request.
References
Shuryak, E. V. Quantum chromodynamics and the theory of superdense matter. Phys. Rep. 61, 71–158 (1980).
Gyulassy, M. & McLerran, L. New forms of QCD matter discovered at RHIC. Nucl. Phys. A 750, 30–63 (2005).
Andronic, A., Braun-Munzinger, P., Redlich, K. & Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 561, 321–330 (2018).
Lattimer, J. M. & Prakash, M. The physics of neutron stars. Science 304, 536–542 (2004).
Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E. & Hessels, J. W. T. A two-solar-mass neutron star measured using Shapiro delay. Nature 467, 1081–1083 (2010).
Antoniadis, J. et al. A massive pulsar in a compact relativistic binary. Science 340, 1233232 (2013).
Cherman, A., Cohen, T. D. & Nellore, A. Bound on the speed of sound from holography. Phys. Rev. D 80, 066003 (2009).
Bauswein, A. et al. Identifying a first-order phase transition in neutron-star mergers through gravitational waves. Phys. Rev. Lett. 122, 061102 (2019).
Fortin, M. et al. Neutron star radii and crusts: uncertainties and unified equations of state. Phys. Rev. C 94, 035804 (2016).
Gandolfi, S., Illarionov, A. Y., Schmidt, K. E., Pederiva, F. & Fantoni, S. Quantum Monte Carlo calculation of the equation of state of neutron matter. Phys. Rev. C 79, 054005 (2009).
Tews, I., Krüger, T., Hebeler, K. & Schwenk, A. Neutron matter at next-to-next-to-next-to-leading order in chiral effective field theory. Phys. Rev. Lett. 110, 032504 (2013).
Kurkela, A., Romatschke, P. & Vuorinen, A. Cold quark matter. Phys. Rev. D 81, 105021 (2010).
Gorda, T., Kurkela, A., Romatschke, P., Säppi, M. & Vuorinen, A. Next-to-next-to-next-to-leading order pressure of cold quark matter: leading logarithm. Phys. Rev. Lett. 121, 202701 (2018).
Hebeler, K., Lattimer, J. M., Pethick, C. J. & Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 773, 11 (2013).
Kurkela, A., Fraga, E. S., Schaffner-Bielich, J. & Vuorinen, A. Constraining neutron star matter with quantum chromodynamics. Astrophys. J. 789, 127 (2014).
Annala, E., Gorda, T., Kurkela, A. & Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter equation of state. Phys. Rev. Lett. 120, 172703 (2018).
Most, E. R., Weih, L. R., Rezzolla, L. & Schaffner-Bielich, J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys. Rev. Lett. 120, 261103 (2018).
Abbott, B. P. et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101 (2017).
Abbott, B. P. et al. GW170817: measurements of neutron star radii and equation of state. Phys. Rev. Lett. 121, 161101 (2018).
Lattimer, J. M. & Prakash, M. Neutron star structure and the equation of state. Astrophys. J. 550, 426–442 (2001).
Gandolfi, S., Carlson, J. & Reddy, S. Maximum mass and radius of neutron stars, and the nuclear symmetry energy. Phys. Rev. C 85, 032801(R) (2012).
Borsányi, S. et al. Full result for the QCD equation of state with 2 + 1 flavors. Phys. Lett. B 730, 99–104 (2014).
Bazavov, A. et al. Equation of state in (2 + 1)-flavor QCD. Phys. Rev. D 90, 094503 (2014).
Müther, H., Prakash, M. & Ainsworth, T. L. The nuclear symmetry energy in relativistic Brueckner–Hartree–Fock calculations. Phys. Lett. B 199, 469–474 (1987).
Akmal, A., Pandharipande, V. R. & Ravenhall, D. G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 58, 1804–1828 (1998).
Typel, S., Röpke, G., Klähn, T., Blaschke, D. & Wolter, H. H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 81, 015803 (2010).
Fattoyev, F. J., Horowitz, C. J., Piekarewicz, J. & Shen, G. Relativistic effective interaction for nuclei, giant resonances and neutron stars. Phys. Rev. C 82, 055803 (2010).
Steiner, A. W., Hempel, M. & Fischer, T. Core-collapse supernova equations of state based on neutron star observations. Astrophys. J. 774, 17 (2013).
Cromartie, H. T. et al. Relativistic shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 4, 72–76 (2020).
Nättilä, J. et al. Neutron star mass and radius measurements from atmospheric model fits to X-ray burst cooling tail spectra. Astron. Astrophys. 608, A31 (2017).
Nättilä, J., Steiner, A. W., Kajava, J. J. E., Suleimanov, V. F. & Poutanen, J. Equation of state constraints for the cold dense matter inside neutron stars using the cooling tail method. Astron. Astrophys. 591, A25 (2016).
Steiner, A. W., Lattimer, J. M. & Brown, E. F. The equation of state from observed masses and radii of neutron stars. Astrophys. J. 722, 33–54 (2010).
Guillot, S., Servillat, M., Webb, N. A. & Rutledge, R. E. Measurement of the radius of neutron stars with high signal-to-noise quiescent low-mass X-ray binaries in globular clusters. Astrophys. J. 772, 7 (2013).
Özel, F. et al. The dense matter equation of state from neutron star radius and mass measurements. Astrophys. J. 820, 28 (2016).
Bogdanov, S., Heinke, C. O., Özel, F. & Güver, T. Neutron star mass–radius constraints of the quiescent low-mass X-ray binaries X7 and X5 in the globular cluster 47 Tuc. Astrophys. J. 831, 184 (2016).
Steiner, A. W. et al. Constraining the mass and radius of neutron stars in globular clusters. Mon. Not. R. Astron. Soc. 476, 421–435 (2018).
Shaw, A. W. et al. The radius of the quiescent neutron star in the globular cluster M13. Mon. Not. R. Astron. Soc. 476, 4713–4718 (2018).
Fraga, E. S., Kurkela, A. & Vuorinen, A. Interacting quark matter equation of state for compact stars. Astrophys. J. 781, L25 (2014).
Tews, I., Margueron, J. & Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 98, 045804 (2018).
Tews, I., Carlson, J., Gandolfi, S. & Reddy, S. Constraining the speed of sound inside neutron stars with chiral effective field theory interactions and observations. Astrophys. J. 860, 149 (2018).
Greif, S. K., Raaijmakers, G., Hebeler, K., Schwenk, A. & Watts, A. L. Equation of state sensitivities when inferring neutron star and dense matter properties. Mon. Not. R. Astron. Soc. 485, 5363–5376 (2019).
Baym, G., Furusawa, S., Hatsuda, T., Kojo, T. & Togashi, H. New neutron star equation of state with quark–hadron crossover. Astrophys. J. 885, 42 (2019).
Bai, Z. & Liu, Y.-X. Determining hadron–quark phase transition chemical potential via astronomical observations. Preprint at https://arxiv.org/pdf/1903.12336.pdf (2019).
Bai, Z. & Liu, Y.-X. Constraining the hadron–quark phase transition chemical potential via astronomical observation. AIP Conf. Proc. 2127, 020030 (2019).
Lindblom, L. Spectral representations of neutron-star equations of state. Phys. Rev. D 82, 103011 (2010).
Lindblom, L. Causal representations of neutron-star equations of state. Phys. Rev. D 97, 123019 (2018).
Holt, J. W., Kaiser, N. & Weise, W. Density-dependent effective nucleon–nucleon interaction from chiral three-nucleon forces. Phys. Rev. C 81, 024002 (2010).
Read, J. S., Lackey, B. D., Owen, B. J. & Friedman, J. L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 79, 124032 (2009).
Haensel, P., Potekhin, A. Y. & Yakovlev, D. G. Neutron Stars 1: Equation of State and Structure (Springer, 2007).
Acknowledgements
We thank I. Tews for helpful discussions and collaboration in early stages of this work. In addition, we acknowledge useful discussions with P. Chesler, N. Jokela, S. Liuti, A. Rebhan, S. Reddy, U. Wiedemann and K. Yagi. The work of E.A., T.G. and A.V. has been supported by the European Research Council (grant no. 725369) and by the Academy of Finland (grant no. 1322507). In addition, E.A. gratefully acknowledges support from the Finnish Cultural Foundation and T.G. from the US Department of Energy (grant no. DE-SC0007984).
Author information
Authors and Affiliations
Contributions
All authors conducted the research together and participated in the preparation and revision of the manuscript. The speed-of-sound interpolation was implemented by T.G. and the spectral interpolation by E.A., both based on an earlier code written by A.K.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Stefano Gandolfi, Constança Providência and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 A comparison of the three interpolation methods considered.
Ranges of allowed equations of state (a), and the corresponding neutron star mass–radius relations (b), are displayed as obtained with the speed-of-sound (green region), piecewise polytropic (black dotted lines), and spectral (orange dashed lines) interpolation methods. In panel b, we show also equations of state that fail to reproduce 2M⊙ stars (cyan region) and those that lead to tidal deformabilities outside the range determined by the gravitational-wave event GW17081719 (purple region).
Extended Data Fig. 2 Limiting the amount of fine structure in the equations of state.
We display equation-of-state bands subjected to the additional constraint of setting a lower limit for the logarithmic segment size in energy density, \(\Delta \ \mathrm{ln}\,\epsilon\). In our analysis of the polytropic-index distributions, we have applied the lower limit \(\Delta \ \mathrm{ln}\,\epsilon >0.5\), which affects the EoS band mainly near the low- and high-density limits.
Extended Data Fig. 3 The central densities of neutron stars of different masses.
The central densities and pressures of different stars are displayed on top of a background showing the ranges of possible neutron star matter equations of state. Maximally massive stars (red dots), 2M⊙ stars (orange squares), and 1.44M⊙ stars (blue diamonds) are shown on top of each other. The color coding of the background refers to the maximal value that the speed of sound squared \({c}_{s}^{2}\) reaches at any density.
Extended Data Fig. 4 The size of the quark core in two-solar-mass neutron stars.
The extent of the quark-matter cores in 2M⊙ neutron stars as a function of the maximal mass \({M}_{\max }\) for each equation of state. The color coding of the points refers to the maximal value that the speed of sound squared \({c}_{s}^{2}\) reaches at any density for the corresponding equations of state.
Extended Data Fig. 5 Comparison of mass–radius predictions to recent observations.
We compare the MR curves obtained with our interpolated equations of state to several recent simultaneous MR measurements. X-ray burst constraints are indicated by solid lines and quiescent low-mass X-ray binary system measurements by dotted (hydrogen atmosphere) or dashed (helium atmosphere) lines. We show examples of measurements obtained with three different methods: direct atmosphere-model fits to the time-evolving X-ray burst spectra (corresponding to the low-mass X-ray binary [LMXB] system 4U 1702–429 [yellow curve])30, cooling-tail method fits to X-ray burst observations (LMXBs 4U 1724−307 [light brown] and SAX J1810.8−2609 [cyan])31, and quiescent LMXB spectra fits to sources with reliable distance measurements (NGC 6304 [dark brown], NGC 6397 [green], M13 [purple], M28 [orange], M30 [black], ωCen [magenta], 47 Tuc X5 [blue], and 47 Tuc X7 [red])32,33,34,35,36,37. For the quiescent LMXB measurements we use public data from refs. 36,37. We assume, for simplicity, no hot spots. The color coding of the regions refers to the maximal value that the speed of sound squared \({c}_{s}^{2}\) reaches at any density for the corresponding equations of state.
Supplementary information
Supplementary Table
This file contains three tabulated representative EoSs. 1. A subconformal EoS with a crossover transition, leading to sizable quark matter cores in massive neutron stars (R = 6.4 km for M\({}_{\max }\)) 1. An intermediate-cs EoS with a crossover transition, leading to sizable quark matter cores in massive neutron stars (R = 5.1 km for M\({}_{\max }\)) 2. A high-cs EoS with a strong first-order phase transition, leading to no quark matter cores.
Supplementary Video 1
A 3D animation of Fig. 2 displaying trajectories of a representative subset of interpolated and hadronic EoSs in a space spanned by the polytropic index γ, the pressure ratio p/pFD, and the squared speed of sound c\({}_{{\rm{s}}}^{2}\). Credit: Jyrki Hokkanen, CSC - IT Center for Science Ltd.
Source data
Source Data Fig. 1
Tables denoting the boundaries of the \({c}_{{\rm{s}}}^{2}\) regions in this EP figure.
Source Data Extended Data Fig. 5
Tables denoting the boundaries of the \({c}_{{\rm{s}}}^{2}\) regions in this MR figure.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Annala, E., Gorda, T., Kurkela, A. et al. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 16, 907–910 (2020). https://doi.org/10.1038/s41567-020-0914-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0914-9