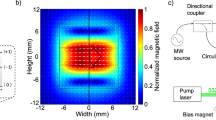
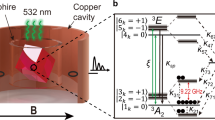
Abstract
Physical systems reach thermal equilibrium through energy exchange with their environment, and for spins in solids the relevant environment is almost always their host lattice. However, recent studies1 motivated by observations by Purcell2 have shown how radiative emission into a microwave cavity can become the dominant relaxation path for spins if the spin–cavity coupling is sufficiently large (such as for small-mode-volume cavities). In this regime, the cavity electromagnetic field overrides the lattice as the dominant environment, inviting the prospect of controlling the spin temperature independently from that of the lattice, by engineering a suitable cavity field. Here, we report on precisely such control over spin temperature, illustrating a novel and universal method to increase the electron spin polarization above its thermal equilibrium value (termed hyperpolarization). By switching the cavity input between resistive loads at different temperatures we can control the electron spin polarization, cooling it below the lattice temperature. Our demonstration uses donor spins in silicon coupled to a superconducting microresonator and we observe more than a twofold increase in spin polarization. This approach provides a general route to signal enhancement in electron spin resonance, or nuclear magnetic resonance through dynamical nuclear spin polarization3,4.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are available for this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Bienfait, A. et al. Controlling spin relaxation with a cavity. Nature 531, 74–77 (2016).
Purcell, E. M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 681 (1946).
Abragam, A. & Goldman, M. Principles of dynamic nuclear polarisation. Rep. Prog. Phys. 41, 395–467 (1978).
Ardenkjr-Larsen, J. H. et al. Increase in signal-to-noise ratio of 10,000 times in liquid-state NMR. Proc. Natl Acad. Sci. USA 100, 10158–10163 (2003).
Schweiger, A. & Jeschke, G. Principles of Pulse Electron Paramagnetic Resonance (Oxford Univ. Press, 2001).
Budoyo, R. P. et al. Phonon-bottlenecked spin relaxation of Er3+:Y2SiO5 at sub-kelvin temperatures. Appl. Phys. Express 11, 043002 (2018).
Astner, T. et al. Solid-state electron spin lifetime limited by phononic vacuum modes. Nat. Mater. 17, 313–317 (2018).
Butler, M. C. & Weitekamp, D. P. Polarization of nuclear spins by a cold nanoscale resonator. Phys. Rev. A 84, 063407 (2011).
Wood, C. J., Borneman, T. W. & Cory, D. G. Cavity cooling of an ensemble spin system. Phys. Rev. Lett. 112, 050501 (2014).
Abragam, A. The Principles of Nuclear Magnetism (Clarenton Press, 1961).
Einstein, A. Strahlungs-emission und Absorption nach der Quantentheorie. Verhandlungen der Deutschen Physikalischen Gesellschaft 18, 318 (1916).
Haroche, S. & Raimond, J.-M. Exploring the Quantum (Oxford Univ. Press, 2006).
Feher, G. & Gere, E. A. Electron spin resonance experiments on donors in silicon. II. Electron spin relaxation effects. Phys. Rev. 114, 1245–1256 (1959).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 11, 143–147 (2012).
Feher, G. Electron spin resonance experiments on donors in silicon. I. Electronic structure of donors by the electron nuclear double resonance technique. Phys. Rev. 114, 1219–1244 (1959).
Mohammady, M. H., Morley, G. W. & Monteiro, T. S. Bismuth qubits in silicon: the role of EPR cancellation resonances. Phys. Rev. Lett. 105, 067602 (2010).
Macklin, C. et al. A near-quantum-limited Josephson traveling-wave parametric amplifier. Science 350, 307–310 (2015).
Wang, Z. et al. Quantum microwave radiometry with a superconducting qubit. Preprint at https://arxiv.org/pdf/1909.12295.pdf (2019).
Xu, M. et al. Radiative cooling of a superconducting resonator. Phys. Rev. Lett. 124, 033602 (2020).
George, R. E. et al. Electron spin coherence and electron nuclear double resonance of Bi donors in natural Si. Phys. Rev. Lett. 105, 067601 (2010).
Pechal, M. et al. Superconducting switch for fast on-chip routing of quantum microwave fields. Phys. Rev. Appl. 6, 024009 (2016).
Williamson, L. A., Chen, Y.-H. & Longdell, J. J. Magneto-optic modulator with unit quantum efficiency. Phys. Rev. Lett. 113, 203601 (2014).
Gely, M. F. et al. Observation and stabilization of photonic Fock states in a hot radio-frequency resonator. Science 363, 1072–1075 (2019).
Rauch, W. et al. Microwave properties of YBa2Cu3O7 − x thin films studied with coplanar transmission line resonators. J. Appl. Phys. 73, 1866–1872 (1993).
Adrian, F. J. Theory of anomalous electron spin resonance spectra of free radicals in solution. Role of diffusion-controlled separation and reencounter of radical pairs. J. Chem. Phys. 54, 3918–3923 (1971).
Wong, S. K., Hutchinson, D. A. & Wan, J. K. S. Chemically induced dynamic electron polarization. II. A general theory for radicals produced by photochemical reactions of excited triplet carbonyl compounds. J. Chem. Phys. 58, 985–989 (1973).
Steger, M. et al. Quantum information storage for over 180 s using donor spins in a 28Si ‘semiconductor vacuum’. Science 336, 1280–1283 (2012).
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Castle, J. G. & Feldman, D. W. Resonance modes at defects in crystalline quartz. Phys. Rev. 137, A671–A673 (1965).
Gayda, J.-P. et al. Temperature dependence of the electronic spin-lattice relaxation time in a 2-iron-2-sulfur protein. Biochim. Biophys. Acta 581, 15–26 (1979).
Zhou, Y., Bowler, B. E., Eaton, G. R. & Eaton, S. S. Electron spin lattice relaxation rates for S = 12 molecular species in glassy matrices or magnetically dilute solids at temperatures between 10 and 300 K. J. Magn. Reson. 139, 165–174 (1999).
Probst, S. et al. Inductive-detection electron-spin resonance spectroscopy with 65 spins/Hz1/2 sensitivity. Appl. Phys. Lett. 111, 202604 (2017).
Weis, C. D. et al. Electrical activation and electron spin resonance measurements of implanted bismuth in isotopically enriched silicon-28. Appl. Phys. Lett. 100, 172104 (2012).
Mansir, J. et al. Linear hyperfine tuning of donor spins in silicon using hydrostatic strain. Phys. Rev. Lett. 120, 167701 (2018).
Pla, J. et al. Strain-induced spin-resonance shifts in silicon devices. Phys. Rev. Appl. 9, 044014 (2018).
Sekiguchi, T. et al. Hyperfine structure and nuclear hyperpolarization observed in the bound exciton luminescence of Bi donors in natural Si. Phys. Rev. Lett. 104, 137402 (2010).
Ranjan, V. et al. Pulsed electron spin resonance spectroscopy in the purcell regime. J. Magn. Reson. 310, 106662 (2020).
Acknowledgements
We thank P. Sénat, D. Duet and J.-C. Tack for technical support, and are grateful for discussions within the Quantronics group. We acknowledge IARPA and Lincoln Labs for providing a Josephson travelling-wave parametric amplifier. We acknowledge support from the European Research Council through grant no. 615767 (CIRQUSS) and through the Superconducting Quantum Networks project, the Agence Nationale de la Rercherche under the Chaire Industrielle NASNIQ, the Region Ile-de-France via DIM SIRTEQ, the Engineering and Physical Sciences Research Council (EPSRC) through grant no. EP/K025945/1, the Horizon 2020 research and innovation programme through grant no. 771493 (LOQO-MOTIONS), the National Centre of Competence in Reseach ‘Quantum Science and Technology’, a research instrument of the Swiss National Science Foundation, and the ETH Zurich.
Author information
Authors and Affiliations
Contributions
B.A., S.P. and P.B. designed the experiment. J.J.L.M. and C.W.Z. provided and characterized the implanted Si sample, on which B.A. and S.P. fabricated the Nb resonator. B.A. performed the measurements, with help from S.P. and V.R. B.A. and P.B. analysed the data. B.A. and V.R. performed the simulations. M.P. realized and tested the superconducting switch in a project guided by A.W. B.A. and P.B. wrote the manuscript. S.P., V.R., A.W., J.J.L.M., D.V., D.E. and E.F. contributed useful input to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Stefan Putz and other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Noise power spectral density measurement.
a, Frequency dependence of the noise power spectral density S measured at Tphon=840 mK for the hot (red circles) and cold (blue circles) switch configurations. Solid lines are fit (see Methods). The blue dashed line indicates the expected Scold(ω)for α=0. b, Still temperature Tphon dependence of S measured at ω = ω0 (open circles) and at ω − ω0 = − 2.7 MHz (open triangles) for both hot (red) and cold (blue) configurations. Solid lines are plot of Shot (red) and Scold (blue) with parameters obtained from the frequency dependence fits performed at all Tphon, and with nTWPA = 0.75.
Extended Data Fig. 2 Temperature dependence of polarization.
Equilibrium polarization of transitions ∣4, − 1 > ↔ ∣5, 0 > and ∣4, 0 > ↔ ∣5, − 1 > measured at B0=62.5 mT (red circles). Several hours are waited at each temperature before recording Ae. Red line is the calculated ΔN(T) for the considered transition at B0=62.5 mT. A second polarisation measurement of the same transitions (black circles) is reported. In this experiment, for each temperature value, B0 is first set to 9.3 mT during 20 min, then it is set to 62.5 mT and finally after 4 min Ae is recorded. The black line is the calculated ΔN(T)for the considered transition at B0=9.3 mT. The polarisation p(T)=\(\tanh (\frac{\hslash {\omega }_{0}}{2kT})\) of a spin 1/2 is also shown for comparison (green). Ae as a function of time (inset) is measured at T=83 mK and B0=62.5 mT after B0 has been set to 9.3 mT for 20 min. The same data are represented in the main plot with the blue arrow.
Extended Data Fig. 3 Simulation of Rabi oscillations.
a, Distribution of the spin-cavity coupling g obtained from the spatial distribution of δB1. b, Rabi oscillations measured at B0=62.5 mT and T =850 mK by varying the amplitude of the second pulse in the Hahn echo sequence (blue circles). The pulse amplitude is normalized to the value \({{\mathrm{P}}_{\pi }}^{\frac{1}{2}}\) corresponding to the maximum in detected signal. The solid green line is the result of the numerical simulation of a spin ensemble described by ρ(g).
Supplementary information
Source Data Fig. 1
Cartesian measurement data.
Source Data Fig. 2
Cartesian measurement data.
Source Data Fig. 3
Cartesian measurement data.
Source Data Fig. 4
Cartesian measurement data.
Source Data Extended Data Fig. 1
Cartesian measurement data.
Source Data Extended Data Fig. 2
Cartesian measurement data.
Source Data Extended Data Fig. 3
Cartesian measurement data.
Rights and permissions
About this article
Cite this article
Albanese, B., Probst, S., Ranjan, V. et al. Radiative cooling of a spin ensemble. Nat. Phys. 16, 751–755 (2020). https://doi.org/10.1038/s41567-020-0872-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0872-2
This article is cited by
-
Lamb shift statistics in mesoscopic quantum ensembles
Quantum Information Processing (2022)